前回の記事で「データ全体の特性を説明する値」である「代表値」で,最も重要な指標である「平均」について触れましたが,平均以外にも代表値として使えるものがあるのでそれらを軽く紹介しておきます.
(追記)全16時間の統計学動画講座を公開しました!☆4.8の超高評価をいただいている講座です.こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください.
目次
真ん中の値である中央値
「データサイエンスのためのPython講座」でも何度か出てきている中央値(median)です.(NumPyの回とか,Seabornのboxplotとか)
中央値については,日常的にもよく使う指標だと思うので特に説明は不要だと思いますが,データを値の大きさ順に並べた時に真ん中にくる値です.中位数ともいいます.(データが偶数個ある場合は真ん中の2つの算術平均をとるのが一般的です.)
前回のりんごの例のように,データの値がだいたい同じような場合には平均を代表値にしても問題ないんですが,外れ値(全体の分布から外れた値)(outlier)があったりすると,平均値を代表値として使うとミスリーディングをする可能性があります.
例えば年収や資産など,金額のデータのように上には上があるようなデータセットでは平均値より中央値を使うのがいいかもしれません.どんなに外れ値が分布からずれていても,中央値はあまり影響を受けませんが,平均は外れ値の影響をもろに受けてしまうので注意です.
その他に留意しておく点として,平均よりも計算量が高くなることを覚えておきましょう.
平均は,値を順々に足して最後にデータ数で割るだけなのでたいして計算量は高くないんですが,中央値は一度データをソートする処理が入るので計算量が高くなります.平均と同じ感覚で大量のデータに使うと大変なことになるので注意ですね!
例えば以下のように,標準正規分布から値をランダムに取り出してNumPyを使って平均と中央値を計算してそれぞれ処理にかかった時間を time.time() を使って比べてみましょう!
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
import numpy as np import time # 標準正規分布からランダムで値を抽出 randoms = np.random.randn(10**7) # 計算前の時間(sec) before_mean = time.time() # 平均を計算 mean = np.mean(randoms) # 平均計算後の時間(sec) after_mean = time.time() print('mean is {} (time:{:.2f}s)'.format(mean, after_mean-before_mean)) # 計算前の時間(sec) before_median = time.time() # 中央値を計算 median = np.median(randoms) after_median = time.time() print('median is {} (time:{:.2f}s)'.format(median, after_median-before_median)) |
|
1 2 |
mean is 0.00015996733320892628 (time:0.01s) median is -4.2001016778634444e-05 (time:0.14s) |
time.time() は,実行したタイミングでの時間を秒単位で返してくれます.Pythonで処理時間を計測するのに使えるので覚えておきましょう.
また,{:.2f}は小数点第二位まで表示します.計測した時間を表示するときに便利なのでこれも合わせて覚えておくといいです◎
標準正規分布から値をランダムに取ってきた平均は当然0に近い値になっていることがわかると思います.中央値も0に近い値になってますね..(標準正規分布は平均0,分散1の正規分布という話はこちらでもやりました.また本講座で詳しく解説したいと思ってますので,「なんのこっちゃ」な人は無視してください)
一番多く出現する値:最頻値
代表値としては平均,中央値ほど使いませんが,最頻値(mode)も代表値の1つです.
最頻値というのは,その分布で最も多く(頻繁に)観測される値です.ヒストグラムを作った時に,山が最も高くなる値ですね!こちらの記事で出てきた確率密度が最も高くなる値でもあります.(確率密度についてはまた改めて説明するので,今はわからなくてOK!)
例えば統計データが,極端にある値に集中している場合は,平均値や中央値よりも最頻値を代表値として用いるのが適していると言える場合もあります.
最頻値は scipy.stats.mode() を使って簡単に取得することができます.
|
1 2 3 4 5 6 |
from scipy import stats # 最頻値と,その数を返す mode, count = stats.mode([6, 2, 4, 5, 1, 3, 5, 3, 4]) # 2つの最頻値が見つかったら,小さい方を返す.今回は3が2つ,4が2つなので3が最頻値として返される print(mode) print(count) |
|
1 2 |
[3] [2] |
結果はNumPy Arrayが2つ(最頻値とそのカウント数)返ってきます.NumPy Arrayで返ってくるのは,たとえば以下のようにndarrayに対しても使えるからですね!
|
1 2 3 4 5 6 7 |
array = np.array([[1, 5, 3, 2], [4, 1, 3, 4], [7, 2, 1, 5], [5, 2, 4, 1]]) mode, count = stats.mode(array, axis=0) print(mode) print(count) |
|
1 2 |
[[1 2 3 1]] [[1 2 2 1]] |
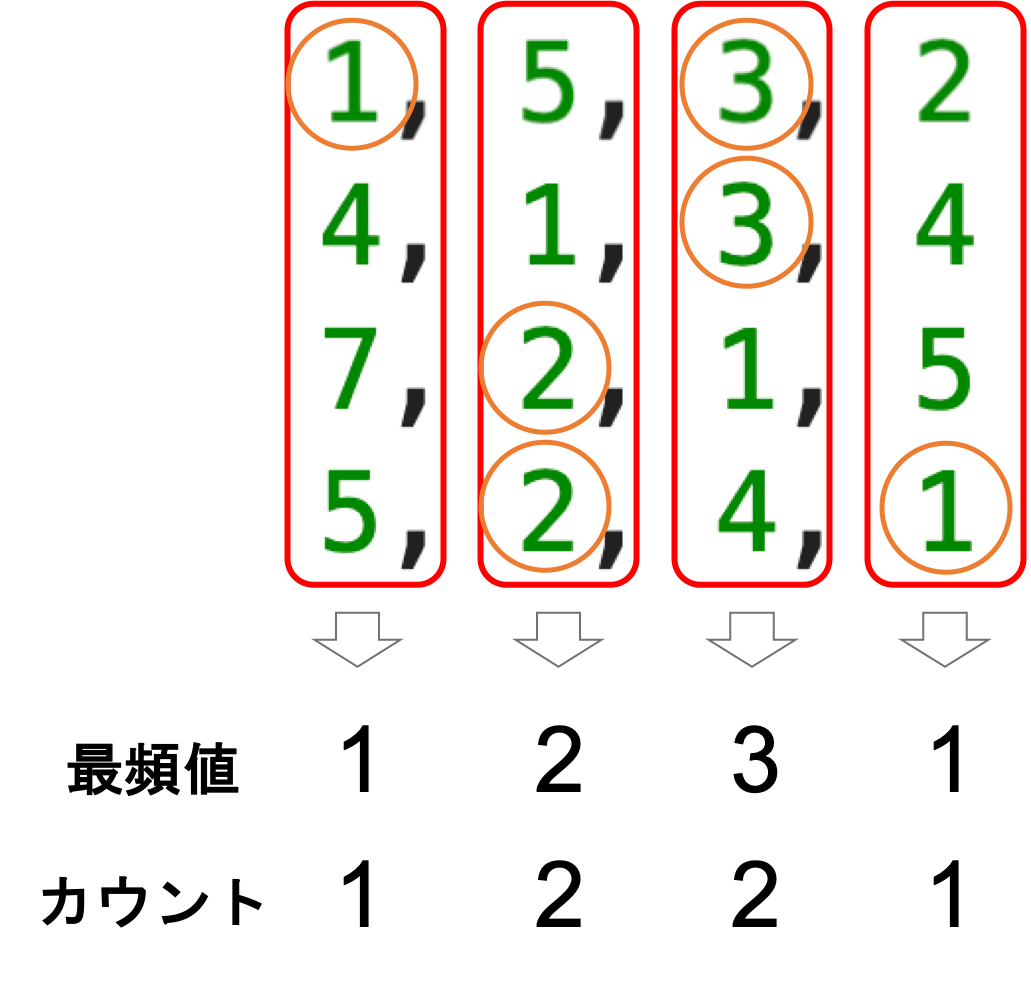
axis引数で,最頻値を計算する軸を変更できるので試してみてください.(デオフォルトは axis=0 です.)
あまりこの関数を使うことは少ないと思いますが,ご参考までに..(最頻値を求めることってそんなに多くないです.)
まとめ
平均以外にも使える代表値として中央値と最頻値を紹介しました.
- 中央値は,データを並べた時に中央に位置する値
- 中央値は,平均に比べ外れ値の影響を受けにくい
- 中央値は,平均に比べ値をソートする必要があるので計算量が大きく処理に時間がかかる
- Pythonで処理時間を計測するには time.time() を使う
- 最頻値は,最も頻繁に出現する値
そんなに難しい話ではないですね!これらの値については,今後統計学で色々な分布を解説する時に当たり前のように使っていくので是非押さえておきましょう!
それでは!
(追記)次回の記事書きました!