ばらつきを表す散布度(範囲と四分位数を使う)【統計学入門④】

前回までの記事で，データを代表する値「代表値」についてみてきました．

この代表値を使えば，データ全体がどういう値を持っているのか，なんとなく知ることはできるでしょう．でも，代表値だけでデータ全体の性質を知るには無理があるケースがありますよね？

カゴに入れたりんごの重さだったら，平均だけでなんとなくそのりんごの重さが伝わると思います．が，例えばあなたが5匹の(犬種の異なる)犬を飼っていたとして，平均の重さだけでその５匹の犬の重さを評価することは難しいですよね？大型犬や小型犬がいる場合，平均の重さだけでは全体の性質を説明する事はできません．

このように各データの値に差が大きい場合は，代表値と合わせて「データの散らばり具合」を指標として出してあげる必要があります．

この「データの散らばり具合」のことを散布度とか分散度と言います．

今回と次回の記事で，散布度として使う指標を紹介します．今回の記事では範囲と四分位範囲，四分位偏差について解説していきます．

（追記）全16時間の統計学動画講座を公開しました！☆4.8の超高評価をいただいている講座です．こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください．

値の範囲

あなたの飼っている犬の重さがそれぞれ10kg, 13kg, 17kg, 20kg, 29kgだったとしましょう．平均の重さは17.8kgですが，この平均値だけでは，５匹の犬がだいたいみんな17.8kgなのか，小型犬から大型犬までいるのかピンときませんよね？

そんな場合，まず第一に思いつく方法としては，この平均の重さに加えて最大値と最小値を伝えてあげることです．つまり，値の範囲ですね．

「私の飼っている犬の平均の重さは17.8kgです」より，「私の飼っている犬の平均の重さは17.8kgで，10kg~29kgの範囲です」と説明された方が一気にデータがどう分布しているのかイメージがつくと思います．

「データの散らばり具合」でいうと，最大値 – 最小値を提示すればいいことになります．この値を範囲(range)と言います．

平均17.8kgで範囲が19kgとわかれば，結構データがバラついてる（少なくとも最小値と最大値が離れている）のがイメージできると思います．

しかし，これだけだと外れ値があった場合にあまり意味のない情報になりかねません．

そこで出てくるのが次に紹介する四分位数を使った指標です．

四分位数を使った範囲と四分位偏差

最小値と最大値のような極端な値だと外れ値に弱いので，もう少し中間に近い値を使って散布度を求めようという作戦です．データをソートした時にデータを４等分する位置にある値(これを四分位数(quartile)と言います．)を使って，四分位偏差(quartile deviation)というのを求めます．

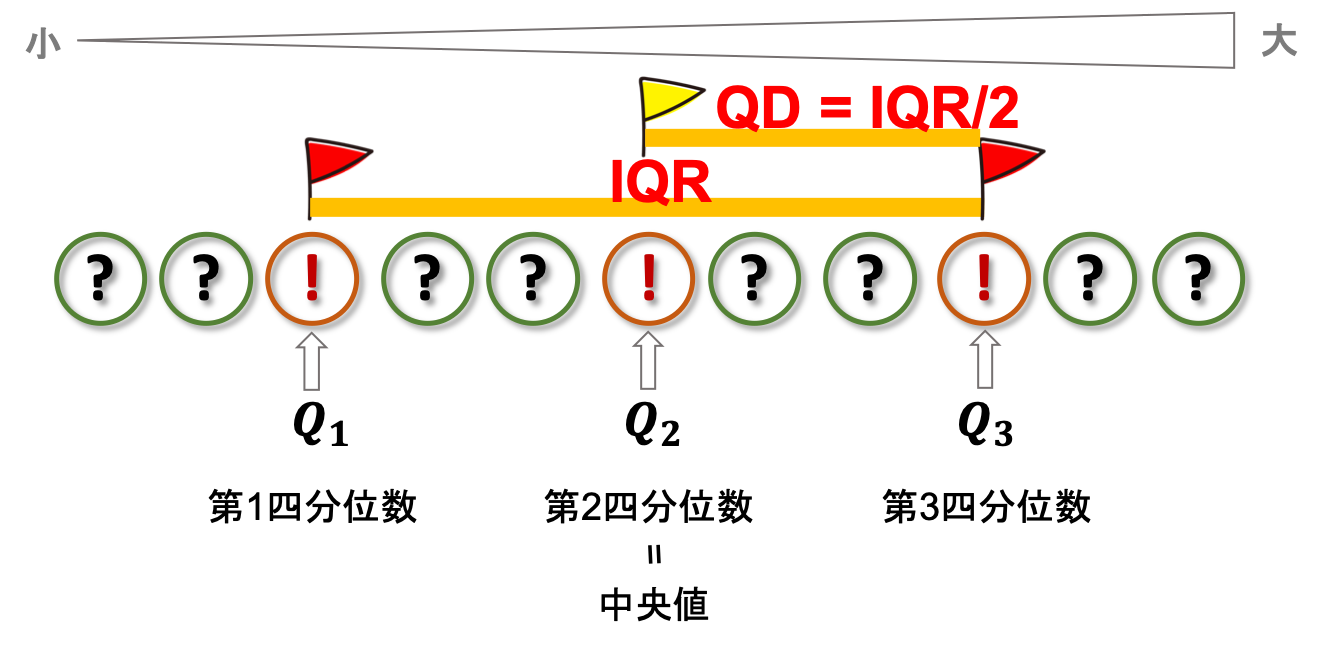
4等分する方法は簡単です．まず真ん中の値を探して，前半と後半に分けます．で，それぞれでまた真ん中の値を見つければOK！データ数が偶数の場合は通常両方の値の算術平均をとります．

それぞれの四分位数を\(Q_1\), \(Q_2\), \(Q_3\)と表し，第1四分位数, 第2四分位数, 第3四分位数と言います．第2四分位数は中央値になることに留意しておきましょう！

そして，\(Q_3-Q_1\)を四分位範囲(interquartile range: IQR)といい，その半分の値\(\frac{Q_3-Q_1}{2}\)を四分位偏差(quartile deviation: QD)といいます．(上の図だと，QDが\(Q_3-Q_2\)のように見えてますが，そういうわけではないので気をつけてください！)

四分位数やIQRについてはboxplotの記事でも紹介しています(ちなみに分位’数’も分位’点’も同じです．個人的にはグラフで表した場合は’点’，実際の値を’数’と呼んでる気がしますが，なんでもいいでしょう．分位’値’とも言います)．

IQRやQDもデータの散らばり具合を表す１つの指標として使います．先ほどの「範囲」よりも外れ値の影響を受けなくてすみます．

IQRはscipy.stats.iqr()で簡単に求めることができます！

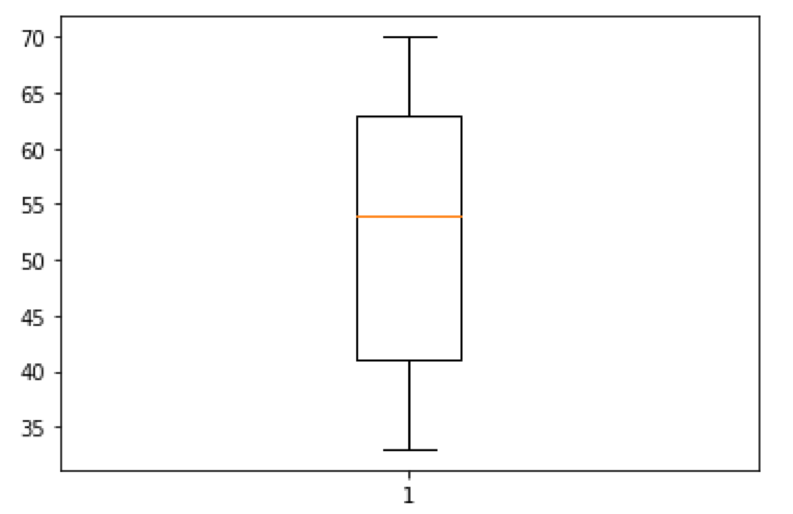
plt.boxplot()についてはこちらの記事を参考にしてください．

範囲と四分位範囲の短所

．．が，どうでしょう，これらの指標ってまだわかりにくいですよね？

範囲は外れ値に弱いという決定的な短所がありますが，四分位範囲や四分位偏差も，全部のデータが使われているわけではないのでデータの散らばり具合を記述するのはちょっと足りない気がしますよね？しかも値自体もイマイチピンときません．

そこで，全部のデータを使用してかつもっとわかりやすい指標として「平均偏差」というのがあります．

そしてその「平均偏差」をもっと扱いやすくした「分散」と「標準偏差」を次回の記事で解説したいと思います！

「散布度」といえば圧倒的に「分散」と「標準偏差」が使われます．聞いたことがあるという人も多いと思いますし，本ブログでも何度か名前だけは出てきています笑

非常に重要な内容なので，次回の記事で改めて紹介しますね！

まとめ

今回はデータのばらつき具合を表す散布度(分散度)について，最大値と最小値を使う範囲と，四分位数を使う四分位範囲および四分位偏差を紹介しました．

• 範囲(range)=最大値-最小値：外れ値に弱い
• 四分位数(quartile):データをソートした時に4等分する位置にある値
• 第2四分位数は中央値
• 四分位範囲(IQR):第3四分位数-第1四分位数．範囲より外れ値に強い
• 四分位偏差(QD):IQRの半分
• ．．．でも結局全データを使って算出しているわけではないので足りない

四分位は統計学的には非常に重要な内容なので，押さえておきましょう．実際のデータサイエンスの現場でも，四分位数を使ってデータの分布を評価したりすることは多いです．上述のboxplotもまさに四分位数を出しています．

でも，散布度の観点からいうと四分位範囲や四分位偏差はまだデータのばらつきを表すのに最適とはいえません．

次回の記事では，散布度の指標の中で最重要項目である分散と標準偏差を紹介します．分散と標準偏差は統計学と機械学習を通してずーーっと出てきます笑　めちゃくちゃ重要な散布度なので必ず押さえておきましょう．

それでは！

(追記)次回の記事です！

絶対にわかる分散と標準偏差(超重要)【統計学入門⑤】