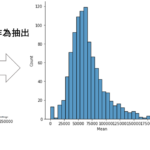
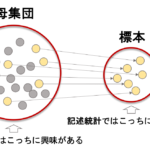
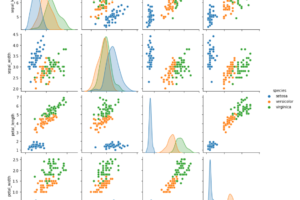
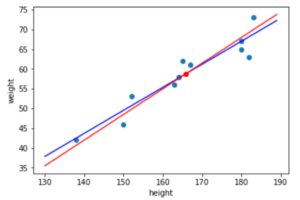
Pythonで学ぶデータサイエンス入門:統計編第24回では,前回の記事で解説した区間推定を実際にやってみたいと思います.
(追記)全16時間の統計学動画講座を公開しました!☆4.8の超高評価をいただいている講座です.こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください.
目次
“比率”を区間推定してみよう!!
区間推定により,標本を使って母数を推定できるという話を前回の記事でしました.

比率(ratio)というのは例えばあるクラスの男女比だったり,内閣の支持率だったり,ある工場で生産される不良品の割合だったりです.これらは現実の世界でもよく目にする指標ですよね?
例えば選挙速報なんかはこの比率の推定をうまく応用しています.なぜ開票率1%で当選確実かどうかが判断できるのでしょうか?残りの99%の人の票は見なくてもいいのでしょうか?
これは,母集団(=投票した人全員)の票の比率を,標本(=母集団の1%の票)から比率を推定しそれがどれくらいの確率で起こりうるかを計算しているわけです.
例えば「99%で支持率(比率)が50%以上」だということがわかれば,ほぼ当選は間違いないだろう,といえるわけですね!
このように,統計学はあらゆる場面で活用されています.それだけ実践的な学問だということが言えると思います.
比率の区間推定の具体的なステップ
前回の記事に区間推定のステップを書いてますが,今回はそれぞれのステップを踏んで実際に比率の区間推定をやってみたいと思います!
今回は比率の例でよく使われる「選挙」を例にとってみましょう.候補者Aさんと候補者Bさんのどちらか片方に投票するシンプルな例を考えてみます.
無効票はなしと考えると,単純に過半数を取得したほうが当選となります.(つまり,比率50%以上を取得すればよい)
仮に投票した人が10万人いたとしましょう.全ての票を開票するのにはかなり時間がかかります.世間はそんなの待ってられません.いち早く結果が知りたいわけです...
そこで活用されるのが標本を使った区間推定ですね!全ての票を開票せずに一部の票を標本として,その標本から母集団(10万人の票)の比率を推定してみましょう!
1. 無作為抽出により標本を作成(すでに標本がある場合は母集団を設定)
まず最初は標本の作成です.すでに標本がある場合は無理のない範囲で母集団を設定しましょう.前回の記事に書いたように,標本は無作為抽出されたものが理想です.が,無作為抽出なんてできないケースが大半です.そういう場合は,”なるべく”無作為っぽくなるように工夫しましょう.例えば今回のケースなら,一つの投票場から標本抽出するのではなくて複数の投票場から抽出するとか,なるべく様々な時間帯の票を抽出するとか.
これは推測統計において最も重要なステップです.今後のステップは全てここで設定した標本&母集団がベースになります.
母集団の設定が曖昧だったり,母集団の設定に無理があるが故にその標本では推定できないのに無理して区間推定しているケースを本当によくみます.注意しましょう!
今回の標本は仮に集まった10万票から1000票(=1%)を無作為抽出して標本を作ったとします.
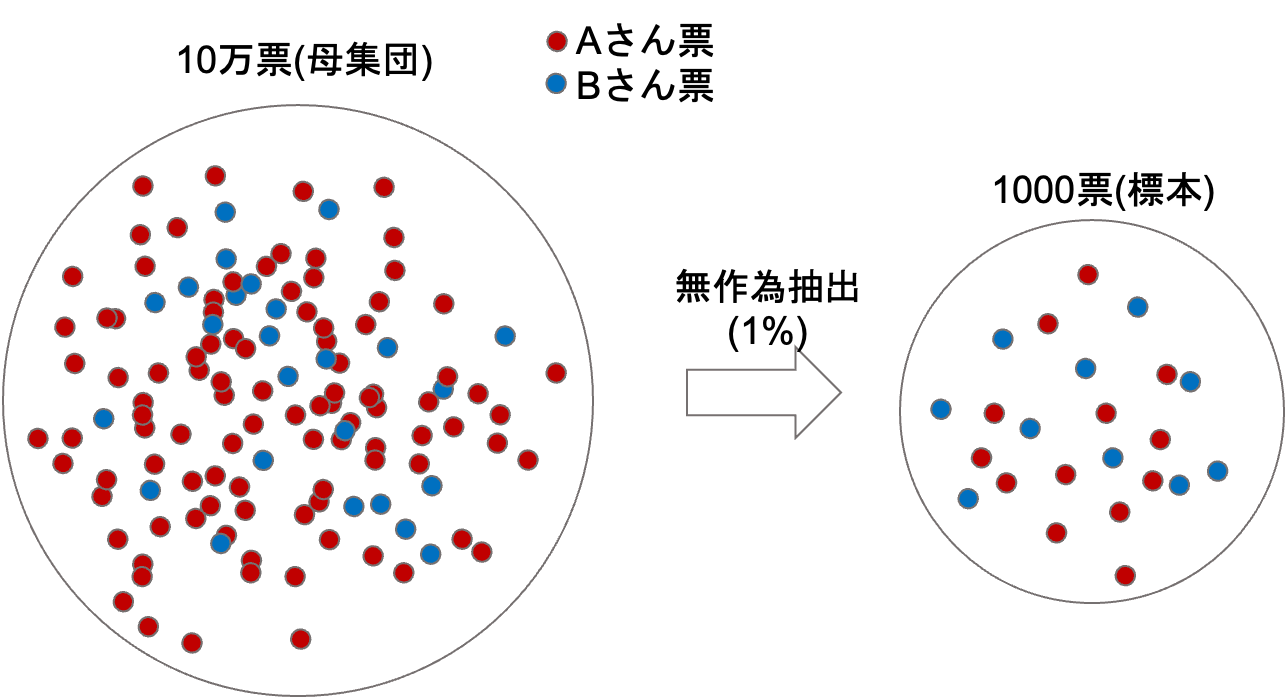
2. 標本から推定量を計算する
今回推定したい母数は比率です.では,標本のどんな値が推定量として使えるでしょうか?
(当然ですが)多くの場合,母数に直接対応する標本統計量が推定量として使われます.つまり,今回だったら標本の比率を推定量として使うわけです.
もし母数が平均だったら,標本の平均を使います.他にも相関係数なんかも標本の相関係数をそのまま推定量として使うことができます.
推定量の期待値が,母数の値に一致する場合,その推定量は「不偏性がある」と言えるという話は第6回や第7回で解説した通りですが,不偏性があるとより推定量として相応しくなります.なので分散の推定量としては標本分散ではなくて不偏分散を使う方がベターです.
同様に,平均や比率も不偏性があることが知られています.標本平均に不偏性があることは第7回で解説している通りです.
Aさんに投票したら1, Bさんに投票したら0と考えると,比率は平均と同じ計算により求めることができます.このことから「比率は平均の特別なケース」と言えますよね?なので,平均も不偏性があるなら比率にも同様に不偏性があると言えるわけです.
今回は仮に,Aさんの票が0.6(60%.つまりAさんの票が600票)(=標本比率)だったとしましょう!

3.信頼区間の設定
1000票の結果を見たら標本比率(Aさんの獲得票率)が0.6(60%)だったからと言って,その背後にある10万人の票の比率も0.6だとは限らないですよね?むしろそうでないだろうと思うほうが自然です.ピッタリと合うことはないはずです.
なので区間を設けましょう.「〇〇%で△△〜□□の間だ!」とすればいいわけです.例えば「95%の確度で母集団の比率は0.56~0.64だろう!」という感じです.「0.6(60%)だ!」と言えればいいんですが,そこまで確かなことは言えないですからね.なのである程度幅をとるわけです.
この区間の事を信頼区間(confidence interval)と言います.よくCIと表すので覚えておきましょう.例えば「95%信頼区間で〜」なんて使い方をします.
そして,ここで設定するのは「どれくらいの確かさ」です.先の例では「95%」の部分です.これが「いやいや,95%じゃ足りないよ,99%くらいの精度で言ってくれ」ということであれば信頼区間は「99%」をとるわけです.そしたらおそらく「母集団の比率は95%なら0.56~0.64だろうと言えるけど,99%だとしたら0.5〜0.7」という感じで範囲がすこし大きくなるはずですよね?幅を大きくとればそれだけ真の母集団の比率がその区間に入っている可能性が高くなるわけですから.
いまいちここで説明している「95%」や「99%」が理解できないかもしれませんが,区間推定のステップを全て説明した後にもっと理解できていると思います.なのでご心配なく!
ではどのように信頼区間を設定すればいいのでしょうか?それは「推定に求める正確さ」次第です.なのでこれは場合によってまちまちです.
ただ,一般的に用いられる信頼区間はほとんどが95%です.「100回中5回間違えるというのはあまり起こらないだろう」というのが一般的な感覚としてあるからです.時々99%信頼区間も使われますが,本講座でも95%信頼区間を扱っていきます.
4. 推定量の標本分布を考える
さて,標本が設定されて,推定量も計算されたなら,今度は標本分布を考える必要があります.(標本分布ってなんだっけ,,という人は第18回を参照してください)

今回標本比率(推定量)は0.6(60%)と算出されました.でもこの値って,たまたま今回の1000票だったからこの値だっただけで,別の1000票だったらまた別の値が計算されますよね?
そこで重要になるのが標本比率の標本分布です.標本分布というのは,標本統計量が従う確率分布のことでした(第18回参照).つまり,今回得られた標本比率0.6というのがたまたま得られた奇跡的な値なのか,よく得られる値なのかが標本分布から分ります.
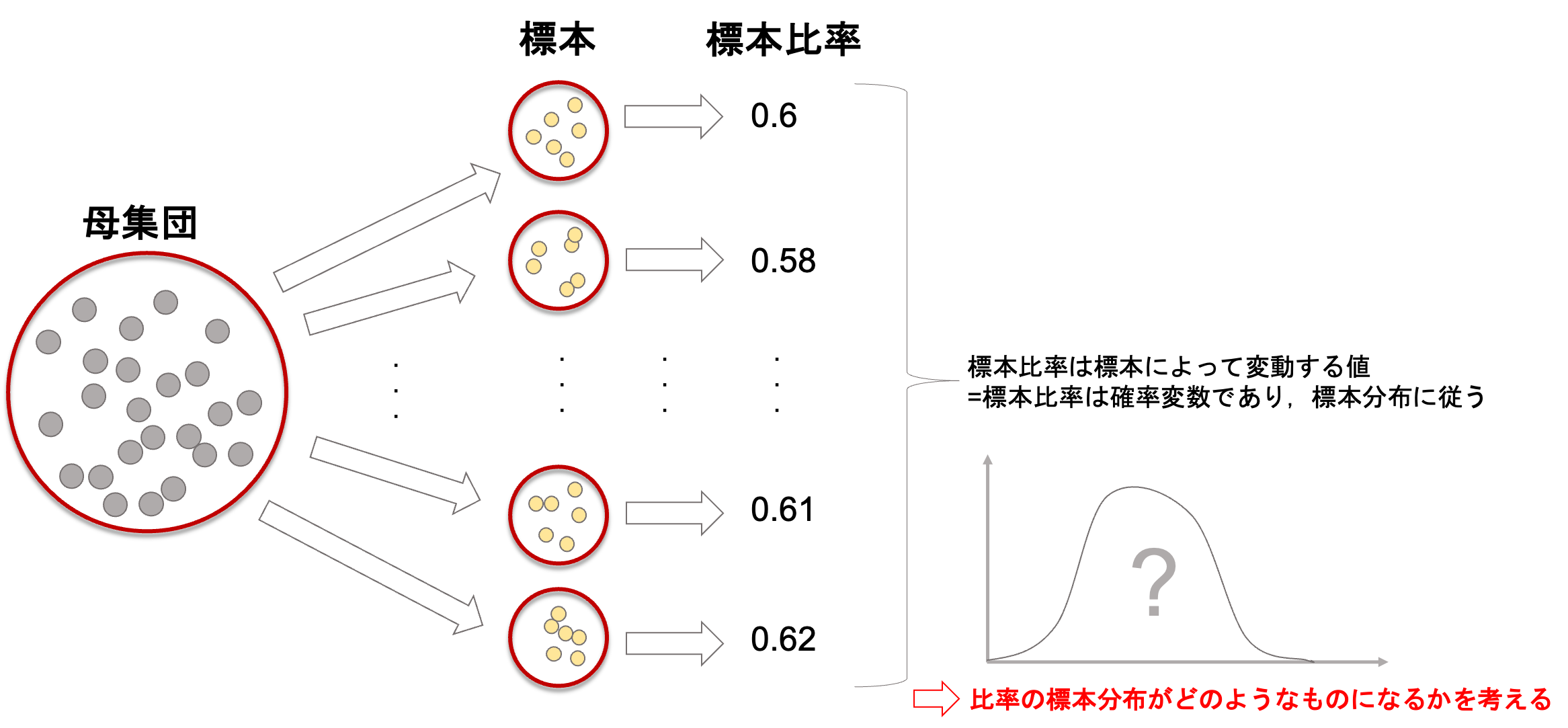
じゃぁどうやって標本分布を得ることができるのか?それは母集団の真の値から作成することができます.

その通り,母集団の真の値がわからないから区間推定をしようとしているのに,区間推定をするのに母集団の真の値が必要というニワトリと卵状態なわけです.
そこで登場するのが”標本比率”なわけですが,まずは母集団の真の比率(ここでは仮に\(p\)としましょう)を使って標本分布がどのようなものになるのか考えてみましょう.
比率の標本分布というのはどういうものになるでしょう?実はこれは二項分布になります.

二項分布については第19回で解説していますが,二項分布というのはどういう確率分布だったかというと,
「1回の観察である事象が起こる確率を\(p\)とします.この観察(や試行)を\(n\)回行った時に,その事象が起こる回数(\(x\))が従う確率分布です.(\(x\)が確率変数です)」
「1回の観察である事象が起こる確率」というのは今回対象としている”比率”と同じですよね?10万票の中から1票をランダムに抽出し,その票がAさんの票である確率は,正に母集団の比率\(p\)と一致するはずです.
「この観察(や試行)を\(n\)回行った時」というのはつまり10万票の中から1000票(=n票)抽出するのと同意ですよね?
つまり二項定理の文は,以下のように言い換えることができます.
「母集団のAさんの票の比率を\(p\)とします.この母集団から無作為に\(n\)票を抽出した時に,Aさんの票数\(x\)が従う確率分布」
Aさんの票数\(x\)がわかれば比率(\(x/n\))がわかるので,Aさんの票数\(x\)が従う確率分布(=二項分布)がわかれば必然的に標本分布が分ります.
そして,第22回に述べたように二項分布の平均は\(np\),分散は\(npq\)(\(q=1-p\))であることがわかっていて,さらにいうとnが十分大きいとき,二項分布は正規分布に近似できるんでした.このあたりが「?」な人は↓の記事を復習しましょう.
(前に学習した内容がいろんなところで活きてきます.是非随時復習しながら講座を読み進めてください!)
したがって,比率\(x/n\)の標本分布は平均\(p\),標準偏差\(\sqrt{pq/n}\)の正規分布で近似することができます.

そして,この標本分布において,95%の確率でとりうる値の区間を考えます.つまり,今回の標本で得られた0.6という値を元に,平均\(p\)が95%の確率でとりうる値を標本分布から算出するのです.
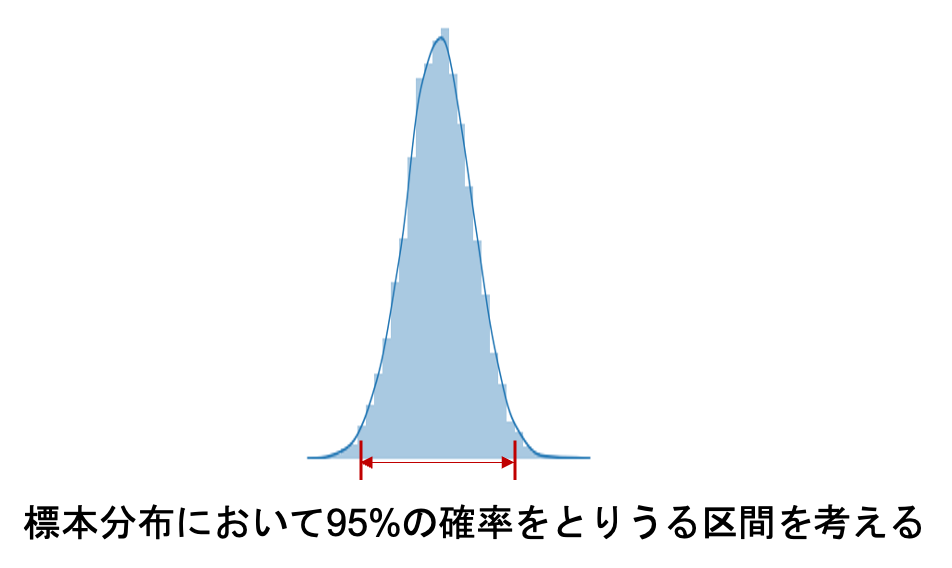
正規分布のまま計算をしてもいいんですが,標準化をした方が分りやすいので,標準化して\(z\)得点を考えましょう.(標準化については第9回を参照してください.標準化は平均を引いて標準偏差で割るんでしたね)
$$z=\frac{x/n-p}{\sqrt{pq/n}}$$
この\(z\)は平均0, 分散1の標準正規分布に従います. この分布を使って,次のステップで信頼区間をもとに母数\(p\)がとりうる値の範囲を算出します.
5. その信頼区間(確からしさ)がとりうる値を標本分布から算出する
この\(z\)というのは,比率\(x/n\)の標準化した標本分布です.例えばこの標本分布において95%でとりうる値の区間を調べれば,95%の確率で\(p\)がとりうる値の区間を計算することができます.
標準正規分布では,-1.96〜1.96の区間で確率が95%になるという話を第8回でしましたね.(1.96という数字は統計学の理論上よく使う数字なので覚えておきましょう!このように標準化をすることで簡単に値を出すことができるのです)
つまり,
$$-1.96<\frac{x/n-p}{\sqrt{pq/n}}<1.96$$
という式に対して\(p\)について解いていけば,母集団の比率\(p\)が95%の確からしさでとりうる値の区間というのが分ります.
これは\(x=600, n=1000, q=1-p\)を代入して解きます.
この数式は最終的に二次不等式の形になり,その解\(p_1\)と\(p_2\)(\(p_1 < p2\))が95%信頼区間で母数(母集団の比率)がとりうる値になります.
計算自体は通常,統計ソフト(SPSSやR,Pythonなど)を使ってやればいいので,通常この数式を自力で解ける必要はありません.
今回の講座は「Pythonで学ぶ」ということでPythonを使ってこの区間推定をやってみたいと思います!具体的にコードを書いて答えが出せると,より今回の説明を理解できると思います.
では,実際に10万票から1000票の標本比率0.6を元に95%信頼区間で母数(比率)を区間推定すると,どのような値になるのでしょうか??Pythonを使ってやってみましょう!
Pythonを使って区間推定をやってみる
それではいつも通りPythonのコードを書いてみましょう!
区間推定は,scipyライブラリのstatsモジュールを使って計算することができます.
今までの記事で,例えば二項分布なら scipy.stats.binorm (第19回),正規分布なら scipy.stats.norm (第22回)を使って任意の確率分布を作ってきました.
区間推定は,それらの確率分布に対して .interval() を呼ぶことによって計算することができます.
今回は,二項分布( scipy.stats.binorm )を使って区間推定をやってみればOKですね.(nが大きければ正規分布に近似されますが,実装する時は正規分布ではなく二項分布を使った方が間違いないかと思います.)
scipy.stats.binorm.interval() の関数に以下の3つの引数を渡しますalpha: 信頼区間(95%なら0.95)
n: 標本の大きさ(試行回数.今回なら1000)
p: 標本比率(60%なら0.6)
|
1 |
stats.binom.interval(0.95, n=1000, p=0.6) |
|
1 |
(570.0, 630.0) |
これだけです.簡単ですね.Pythonに限らず統計ソフトはコードを一行書けば全部やってくれるものがほとんどなので,理論を理解してなくても使えてしまうんですよね.でも理論をちゃんとわかってないと,間違った確率分布を使ってしまったり計算結果を正しく使えないので注意しましょう!
結果をみると570と630という二つの数字がtupleで返ってきました.これは,「何度も1000票の標本を無作為抽出した場合,95%はAさんの票が570票~630票である」ということです.
これはつまり,「母集団の比率は0.57(57%)〜0.63(63%)の間にあることが95%確かである」ということですね.
95%信頼区間とはどういうことなのか?(95%の確からしさとは)
95%信頼区間というのは,「繰り返し区間推定をしたとき,95%の確率で真の母数がその区間にあること」です.
つまり,100回標本を無作為抽出して同様に区間推定をしたら,約95回は真の母数をその区間に含んでいるということです.
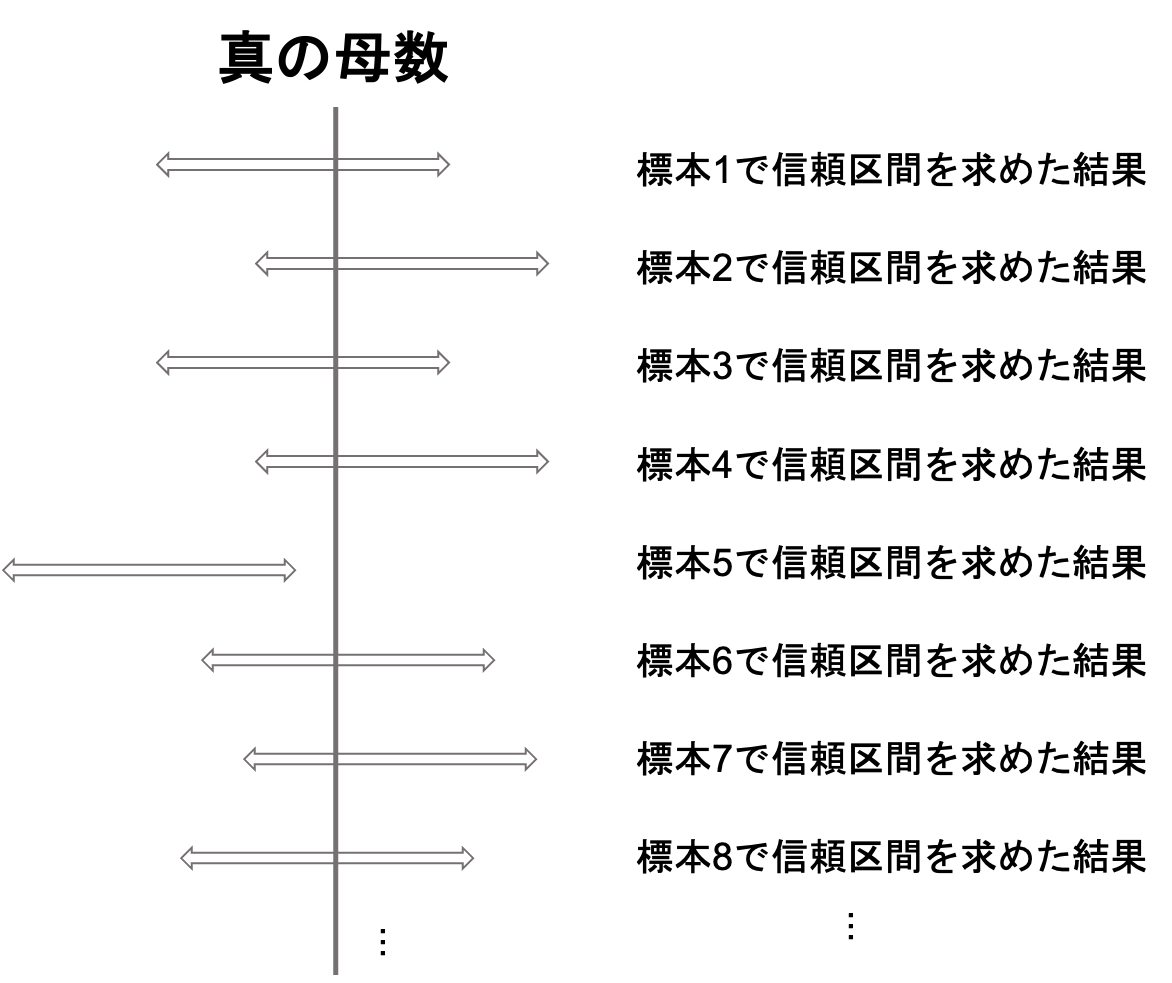
今回の標本から95%信頼区間で区間推定をした結果「母集団の比率は0.57(57%)〜0.63(63%)の間にあることが95%確かである」ことが言えましたが,
これをまた別の1000票で区間推定をしたら例えば0.56~0.62のように,標本比率の変動により少し値がずれるはずです.また別の1000票だったら,,,と,何度も標本を取って区間推定をしたら95%は正しく推定できてますよ,というのが95%信頼区間の意味です.なので,今回の結果である0.57~0.63というのは,5%の確率で間違ってるかもしれないということですね.
「95%の”確率”で母集団の比率は0.57(57%)〜0.63(63%)の間にある」という言い方をすると少し語弊がある可能性がでるので注意しましょう.母集団の真の比率は確率的に変動する値ではなく,固定の値です.なのであたかも母集団の比率が確率変数であるかのように言うのは(厳密に言うと)正しくありません.今回確率的に変動するのは,母集団の真の比率ではなく,区間である0.57(57%)〜0.63(63%)です.これは標本の変動によって変わってきます.なので,「”母集団の比率は0.57(57%)〜0.63(63%)の間にある”という結果が95%の確率で正しい」と言った方が正確です.
今回は1000票のみで信頼区間を出しましたが,それでも95%の信頼区間で0.57~0.63という比率を出すことができました.この信頼区間を例えば99.99%とすると,0.539〜0.66となります(上記のpythonのコードでalpha引数に0.9999を渡してください).
つまり,この時点でAさんは当選確実だと言えると思います.(実際の選挙速報では他の要素も考慮しているはずですが,基本的な考え方はこの信頼区間を応用しています.)
まとめ
長くなってしまいましたが,今回の記事で学習した内容をおさらいしてみましょう!
- 比率の区間推定は身近なところで使われている
- 標本は無作為抽出が理想.すでに標本がある場合は無理な母集団を設定しないこと
- 推定量に使う統計量は,推定したい母数と一致するのが一般的
- 母集団の比率の推定量は標本比率
- 標本比率の標本分布は二項分布になる(十分に標本が大きい場合は正規分布に近似できる)
- 標準化することで,95%の区間の値(-1.96 ~ 1.96)を簡単に取得できる
- stats.<確率分布>.interval()を使うことで簡単に区間推定を算出できる
- 95%信頼区間というのは,「区間推定した結果が95%の確率で合っている」ということである(「母数が95%の確率でその区間にある」という言い方は厳密にいうと正しくない)
今回の記事では実践的な統計の問題に取り組みました.今回の記事だけでも今まで学習した色々な統計の知識を使ってきました.
今後も色々と過去に学習した内容が出てきますので適宜アヤシイと思うところは復習しながら進めていきましょう!
次回は比率と同じくらい(むしろそれ以上??)よくでてくる「平均」の区間推定をやっていきたいと思います!
それでは!
(追記)次回の記事書きました!