超重要！標準化と偏差値ってなに？？z得点とT得点【統計学入門⑨】

こんにちは，米国データサイエンティストのかめ(@usdatascientist)です．

（追記）全16時間の統計学動画講座を公開しました！☆4.8の超高評価をいただいている講座です．こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください．

前回の記事では最も重要な散布度である「標準偏差」を使って，あるデータが分布のどの辺りに位置しているか検討をつけるやり方を紹介しました．

今回の記事ではもう１つ重要な標準偏差の使い方を紹介します．

前回の記事の最後にもいいましたが，平均と標準偏差を使うことで，異なるデータ群間のデータを比較することができます．

どういうことかというと，例えばある中学校で実施したテストと，隣の中学校で実施したテストをそのテストの点数だけみて，どちらの成績が良かったかを比較することはできません．が，平均と標準偏差を使ってそれぞれの中学校の中でどの位置にいるかを計算することによって，テストの成績を相対的に比較することができます．

「え？そんなことできるの？」って思うかもしれませんが，これを応用したのが「偏差値」です．

今回の内容も，今後説明する統計学の理論構成に非常に重要な内容になってますので，ちゃんと押さえておきましょう！

z得点に変換することで，異なるデータ群間で比較可能になる

z得点，，，なんだかかっこいい名前ですね．

前回の記事の通り，平均値から標準偏差の何倍だけは離れているかによってそのデータの位置が大体分かるんでした．

これはつまり，たとえデータ群が違っていても(上の例でいうと中学校が違っていても)，あるデータがそのデータ群の平均点から標準偏差の何倍離れているのかという値を使えば他のデータ群のデータと比較できそうですよね？

例えば，ある中学校Aにいる山田くんの英語のテスト40点と，隣の中学校Bの田中くんの英語テスト60点は，このテストの数字だけではどちらが英語が得意なのか比較することはできません．(もしかしたら中学校Aの英語テストが難しすぎて，山田くんは中学校Aではトップクラスだったかもしれません．)

これを山田くんと田中くんがそれぞれの中学校で「平均値から標準偏差の何倍離れているのか」を計算すれば，少なくともお互い自分の中学校でどのレベルなのかが分かるので，それを比較しよう！ということです．

結論からいうと，これは以下の式で求めることができ，この値をz得点(z-score)と言います．(よく$z$を使って表すので覚えておきましょう)

$$z=\frac{x-\bar{x}}{s}$$

いつも通り，$\bar{x}$は平均，$s$は標準偏差です．

これはなにをしているかというと，データの平均を0，標準偏差(分散)を1に変換しているんですね．これを標準化(standardize)すると言います．

標準化は非常に重要な変換で，データサイエンスではめちゃくちゃよく使います．(扱う値は基本全て標準化して扱うと思っておいてもいいくらい)

本当にこの変換で平均が0, 標準偏差が1になるのか，Pythonで確認してみましょう！

import numpy as np
data = [0, 10, 20, 25, 27, 30, 43, 56, 68, 70]
mean = np.mean(data)
std = np.std(data)
#標準化
z = (data - mean) / std
print('standardized data(z): {}'.format(z))
print('mean: {:.2f}'.format(np.mean(z)))
print('std: {}'.format(np.std(z)))

import numpy as np

data = [0, 10, 20, 25, 27, 30, 43, 56, 68, 70]

mean = np.mean(data)

std = np.std(data)

#標準化

z = (data - mean) / std

print('standardized data(z): {}'.format(z))

print('mean: {:.2f}'.format(np.mean(z)))

print('std: {}'.format(np.std(z)))

standardized data(z): [-1.54799532 -1.10444365 -0.66089199 -0.43911615 -0.35040582 -0.21734032
  0.35927685  0.93589402  1.46815602  1.55686636]
mean: 0.00
std: 1.0

standardized data(z): [-1.54799532 -1.10444365 -0.66089199 -0.43911615 -0.35040582 -0.21734032

0.35927685 0.93589402 1.46815602 1.55686636]

mean: 0.00

std: 1.0

ちゃんと平均0, 標準偏差1になっているのが分かると思います．

もしPythonはよくわからない！っていう方は，先にこちらのブログ講座と動画講座でPythonを一通り勉強しておくことを強くお勧めします．自分でコードを書きながら統計学を学ぶことで，統計の理論が身についていきます．数式や文章を眺めているだけだと，統計学や機械学習の習得はなかなか難しいので．

さて，この標準化ですが，データサイエンスでは本当によく使うのでそれ用の関数が当然用意されています．

今回はPythonで機械学習をするのによく使うscikit-learnというライブラリの preprocessing というモジュールにある StandardScaler を使って標準化してみたいと思います！

標準化は，機械学習でもほんっっっとによく使います．標準化しないでデータをそのまま扱えないケースが多いんですよ．さっきの例で，山田くんと田中くんのテストの点数をそのまま比べられないのと同じように，機械学習でなにかモデルを学習させるときには，データの前処理(preprocessing)で標準化することが多いです．(なので preprocessing モジュールに入っているんですね！)

scikit-learnは import sklearn でインポートすることができます．

from sklearn.preprocessing import StandardScaler
data = np.array([0, 10, 20, 25, 27, 30, 43, 56, 68, 70])
print('data shape: {}'.format(data.shape))
data = np.expand_dims(data, axis=-1)
print('reshaped data shape: {}'.format(data.shape))
# インスタンス作成
scaler = StandardScaler()
# fit_transformの引数にはrank2のnumpy arrayである必要がある
scaled = scaler.fit_transform(data)
print(scaled)

from sklearn.preprocessing import StandardScaler

data = np.array([0, 10, 20, 25, 27, 30, 43, 56, 68, 70])

print('data shape: {}'.format(data.shape))

data = np.expand_dims(data, axis=-1)

print('reshaped data shape: {}'.format(data.shape))

# インスタンス作成

scaler = StandardScaler()

# fit_transformの引数にはrank2のnumpy arrayである必要がある

scaled = scaler.fit_transform(data)

print(scaled)

data shape: (10,)
reshaped data shape: (10, 1)
[[-1.54799532]
 [-1.10444365]
 [-0.66089199]
 [-0.43911615]
 [-0.35040582]
 [-0.21734032]
 [ 0.35927685]
 [ 0.93589402]
 [ 1.46815602]
 [ 1.55686636]]

data shape: (10,)

reshaped data shape: (10, 1)

[[-1.54799532]

[-1.10444365]

[-0.66089199]

[-0.43911615]

[-0.35040582]

[-0.21734032]

[ 0.35927685]

[ 0.93589402]

[ 1.46815602]

[ 1.55686636]]

上の例と比べてみましょう．標準化された値が同じであることが分かると思います．

さて，今回は sklearn.preprocessing.StandardScaler を使いましたが，これはクラスと呼ばれるもので，オブジェクト指向の書き方をします．(前にmatplotlibでも似たようなことをしましたね)

(オブジェクト指向については以下のの動画講座でかなり詳しく解説をしているので勉強したい人は是非受講してください．☆4.8の超高評価でPythonの重要な用法を全て一通り学べます．)

【決定版】Python入門動画講座を公開しました【超高評価でベストセラー】

scaler = StandardScaler() とすると，StandardScalerクラスを基に scaler というインスタンスを生成することができます．
オブジェクト指向が慣れていないと理解しがたいところかもしれませんが，簡単にいうと，このStandardScalerというクラスには，標準化する機能が書いてある設計図があって，その設計図から今回は scaler というモノ(インスタンス)を作ったわけです．当然，このscalerには標準化する機能があって，それを .fit_transform() 関数で実行しています．

まぁコードを読めばそんなに難しくないとは思いますが，慣れましょう．

.fit_transform() で，引数に入れたndarrayを標準化します．この時， .fit_tranform() はrank=2のndarrayを受け取るので，事前に np.expand_dims() でrank=2にしておきます．(この辺りが「？」な人はこちらを参考にしてください．)

まぁこのあたりは，適宜レファレンスを見ながら進めていけばいいです．覚えるのではなく，エラーを出してrankを2にすることに気付ければそれでいいのです． sklearn.preprocessing.StandardScaler はよく使うので，このモジュール自体は覚えておきましょう

偏差値はz得点の派生系

偏差値(T-score)というのは「平均50,　標準偏差10」に標準化した値です．

なんとなく偏差値70がかなりトップクラスで，偏差値50が平均レベルっていうイメージありましたよね？

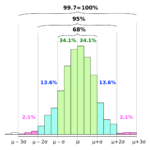
前回の記事で説明したとおり，95%のデータが平均±2*標準偏差に収まるので，偏差値70はおそらくトップ2.5%レベルだろうというのが分かると思います．

偏差値80~100って聞いたことないですよね？これも平均±3*標準偏差に全体が収まることを考えると納得できると思います．

偏差値を求めるには，先ほどのz得点に10を掛けて50を足せばOKです．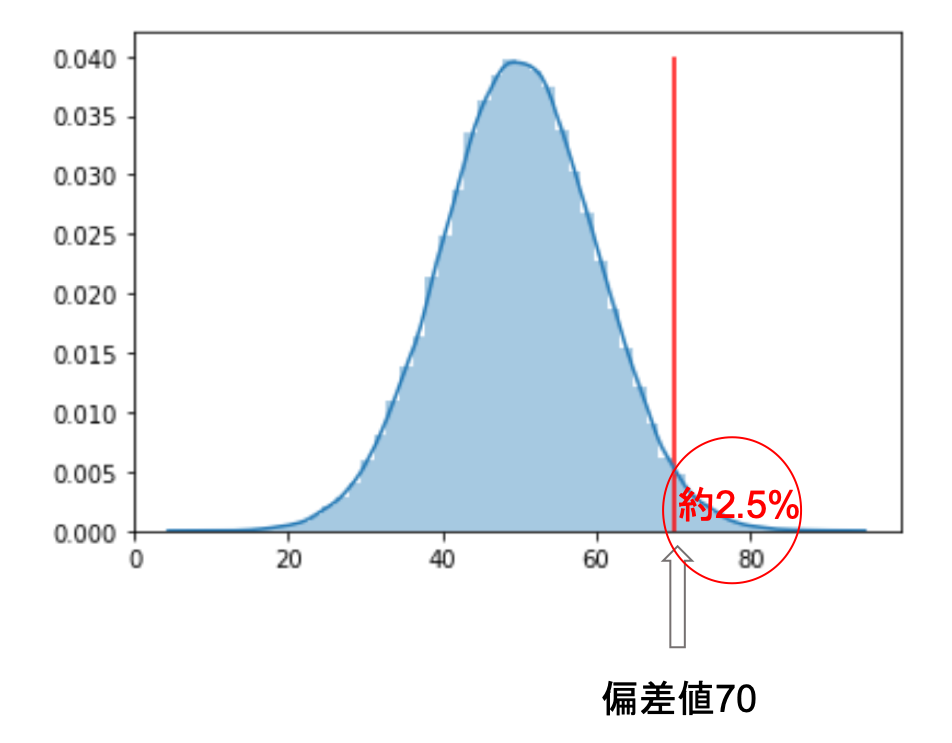

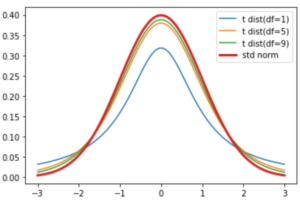
ちなみに，約2.5%になるのは左側(偏差値30以下)も約2.5%で足して約5%ということになります．上の図は以下のコードで描画しました．標準正規分布は平均0, 標準偏差1の正規分布なので，標準正規分布の”標準”というのは，標準化された正規分布であることが分かると思います．(なので，今回は標準正規分布からランダムに値を取得する np.random.randn() 関数を使っています．詳しくはこちら)

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
samples = np.random.randn(100000)
tscore = samples*10 + 50
sns.distplot(tscore)
plt.vlines(70, 0,0.04, 'r')