t分布を超わかりやすく解説(t分布で区間推定！)【統計学入門26】

こんにちは，米国データサイエンティストのかめ(@usdatascientist)です．

データサイエンス入門:統計編第26回です．

（追記）全16時間の統計学動画講座を公開しました！☆4.8の超高評価をいただいている講座です．こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください．

前回の記事で平均の区間推定をやったんですが，今回の記事では平均の区間推定の時にでてくるt分布(student’s t distribution)について解説をしていきます．

t分布，，，単語だけは知ってるけど今まで避けて通ってきました！

という人も多いと思います笑

でもこのt分布は統計学の理論上重要な確率分布になるので，今回の記事でしっかり押さえておきましょう！

1 t分布ってなに？？
2 t分布を見てみよう！
3 t分布を使って平均値の区間推定をしてみよう！
4 t分布を使うのか正規分布を使うのか
5 まとめ

t分布ってなに？？

結論からいうと「平均$\bar{x}$の標本分布において，母集団の標準偏差$\sigma$の代わりに標本標準偏差$s’$を用いた場合の標準化後の平均$\bar{x}$が従う確率分布」です．

前回の記事で平均の標本分布は，平均$\mu$, 分散$\frac{\sigma^2}{n}$の正規分布になるんでした．(※母集団の平均を$\mu$および母集団の標準偏差$\sigma$とする)

これを標準化(第9回参照)した

$$z=\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n}}}$$

を考えます．$z$は標準正規分布に従うことから，(第8回参照)

$$-1.96<\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n}}}<1.96$$

として区間推定をしていたんでした．

でもこの式，母集団の標準偏差$\sigma$を使ってます．

通常これは未知の値です．(母集団の平均$\mu$がわからないから推定しようとしているのに，標準偏差$\sigma$がわかってるなんてことはないですからね)

この母集団の標準偏差$\sigma$の代わりとして標本標準偏差$s’$を使っていたんでした．標本標準偏差$s’$は不偏分散$s’^2$の平方根であることに注意しましょう！

$$s’^2=\frac{1}{n-1}\sum{(x_i-\bar{x})^2}$$

$n$ではなくて$n-1$で割っていることに注意してください．$n-1$で割る理由は第7回で詳しく解説しています

つまり，平均の区間推定をする際に$\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n}}}$ではなくて$\frac{\bar{x}-\mu}{\frac{s’}{\sqrt{n}}}$が従う確率分布を考える必要があります．この分布をt分布と呼びます

$$t=\frac{\bar{x}-\mu}{\frac{s’}{\sqrt{n}}}$$

つまり，標準正規分布の代わりになるものがt分布だということですね！

t分布を見てみよう！

数式ばっかで疲れたよ〜

では，実際にt分布がどのような分布になっているか見てみましょう！標準正規分布は平均0, 分散1の正規分布ということで，パラメータはなく一意に定まる確率分布でした．

t分布は，$n-1$というパラメータによって形状が変わります．これは，不偏分散が$n-1$で割っているところからもわかるように，$n-1$がt分布の唯一のパラメータということになります．

(この$n-1$を自由度(degree of freedom)と言います．)

それでは，statsモジュールの stats.t を使って実際にどのような分布になるのか見てみましょう！( .pdf() については第21回や第22回でも出ましたね .pdf はprobability density functionの略で，入力した引数に対する確率密度関数の結果を返してくれます．)

import numpy
import matplotlib.pyplot as plt
from scipy import stats
%matplotlib inline

x = np.linspace(-3, 3, 100)
for df in range(1, 6):
    t = stats.t.pdf(x, df)
    plt.plot(x, t, label=f"df={df}")
plt.legend()

import numpy

import matplotlib.pyplot as plt

from scipy import stats

%matplotlib inline

x = np.linspace(-3, 3, 100)

for df in range(1, 6):

t = stats.t.pdf(x, df)

plt.plot(x, t, label=f"df={df}")

plt.legend()

stats.t.pdf() には x と df (自由度)を引数として入れます．今回は自由度でどれだけ形が変わるのかわかるように， df に 1 ~ 5 を入れて描画してみました．

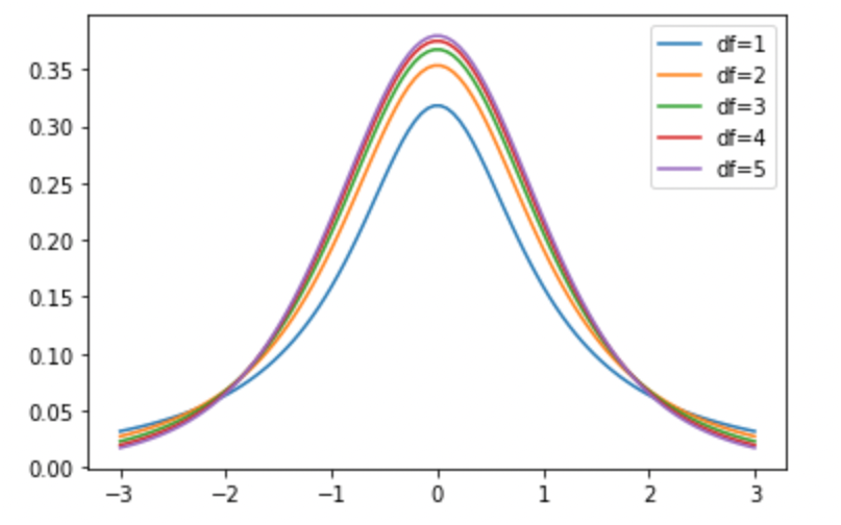
形は(標準)正規分布に似ていてベル型です．自由度が小さいと裾野が長く，自由度が大きくなるにつれ徐々に中心の確率が高く裾野が短くなっているのがわかります．

標準正規分布と比べてみましょう．標準正規分布は stats.norm.pdf(x, loc=0, scale=1) を使えばOKです．

x = np.linspace(-3, 3, 100)
z = stats.norm.pdf(x, loc=0, scale=1)
for df in range(1, 10, 4):
    t = stats.t.pdf(x, df)
    plt.plot(x, t, label=f"t dist(df={df})")
plt.plot(x, z, label='std norm', linewidth=3)
plt.legend()

x = np.linspace(-3, 3, 100)

z = stats.norm.pdf(x, loc=0, scale=1)

for df in range(1, 10, 4):

t = stats.t.pdf(x, df)

plt.plot(x, t, label=f"t dist(df={df})")

plt.plot(x, z, label='std norm', linewidth=3)

plt.legend()

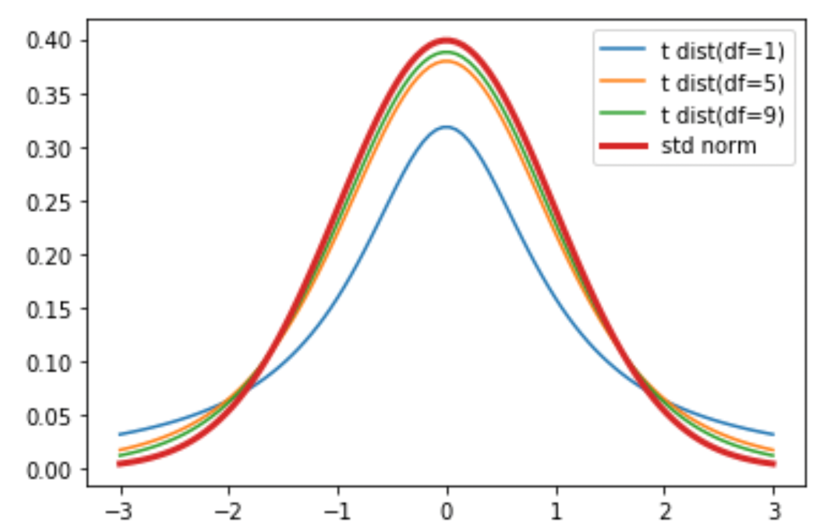
太い赤い線で描かれているのが標準正規分布です．自由度を上げていくと，標準正規分布に近似していくのがわかると思います．

これはつまり「大標本であればt分布を使わなくても標準正規分布で考えてOKだよね」ということですね．

自由度が小さいt分布は裾野が長くなっていますが，これは95%をとりうる区間が広くなることを意味しています．

標準正規分布における95%信頼区間と，自由度1のt分布における95%信頼区間の値をみてみましょう！

これらは， .interval() で調べればよさそうですね！( .interval() については前回の記事と前々回の記事で出てきています．)

標準正規分布はいままでやってきた通り，当然-1.96~1.96となります．

x = np.linspace(-3, 3, 100)
left, right = stats.norm.interval(0.95, loc=0, scale=1)
z = stats.norm.pdf(x, loc=0, scale=1)
plt.plot(x, z)
plt.axvline(left, c='r')
plt.axvline(right, c='r')
print(left, right)

x = np.linspace(-3, 3, 100)

left, right = stats.norm.interval(0.95, loc=0, scale=1)

z = stats.norm.pdf(x, loc=0, scale=1)

plt.plot(x, z)

plt.axvline(left, c='r')

plt.axvline(right, c='r')

print(left, right)

-1.959963984540054 1.959963984540054

1	-1.959963984540054 1.959963984540054

これに比べ自由度2のt分布は

x = np.linspace(-5, 5, 100)
left, right = stats.t.interval(0.95, df=2)
t = stats.t.pdf(x, df=2)
plt.plot(x, t)
plt.axvline(left, c='r')
plt.axvline(right, c='r')
print(left, right)

x = np.linspace(-5, 5, 100)

left, right = stats.t.interval(0.95, df=2)

t = stats.t.pdf(x, df=2)

plt.plot(x, t)

plt.axvline(left, c='r')

plt.axvline(right, c='r')

print(left, right)

-4.302652729911275 4.302652729911275

1	-4.302652729911275 4.302652729911275

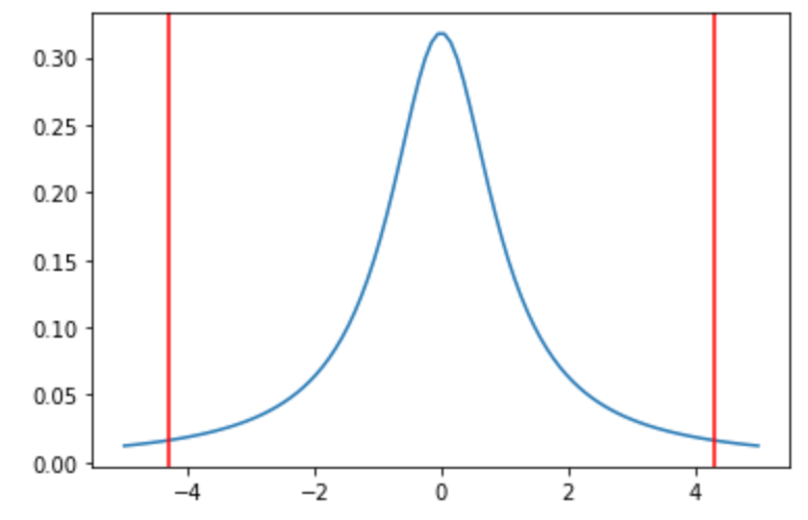
かなり範囲が広いですよね？？

これは自由度2, つまり n=3 という標本が非常に少ないケースでは，それだけ95%の信頼区間の値の幅が大きくなるということです．(自由度を大きくすると，裾野が短くなり中央の確率が上がっていくので，95%の面積を計算するとx軸の値の幅が小さくなるイメージです．)

標本を大きくするとそれだけ推定した際の区間が狭くなるのは，イメージつきやすいと思います．

↓の例は自由度2(赤)と自由度10(緑)のt分布とその95%区間です．自由度が大きくなると95%区間が狭まってるのがわかると思います．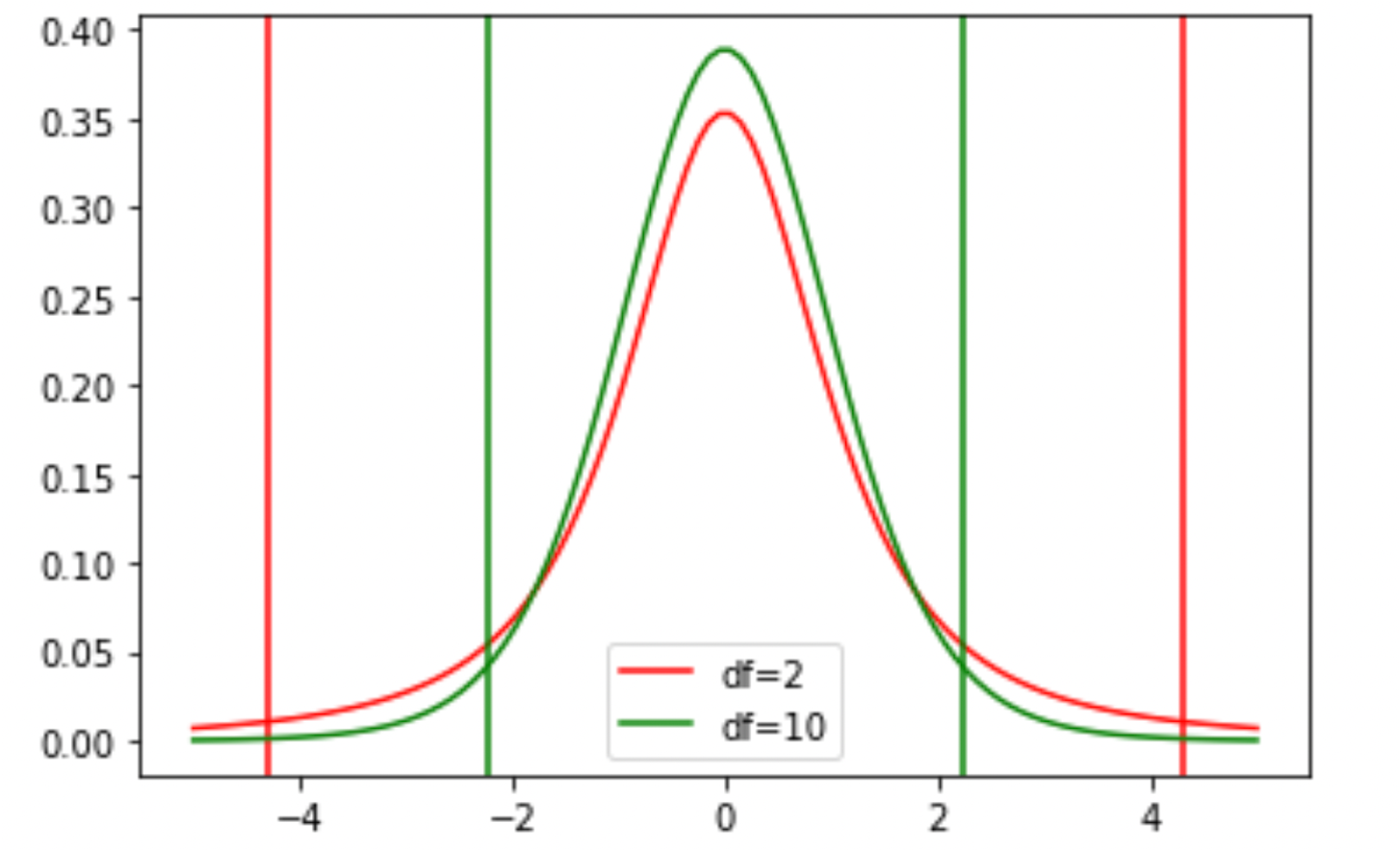

つまりこれは，「平均$\bar{x}$の標本分布において母集団の標準偏差$\sigma$の代わりに標本標準偏差$s’$を用いた場合，推定する区間を広く取る必要がある」ことを意味します．

でも，標本の大きさ$n$を大きくしたら標本標準偏差$s’$は母集団の標準偏差$\sigma$に限りなく近くなると考えられるので，それによる影響も少なくなっていくということですね！

t分布を使って平均値の区間推定をしてみよう！

前回と同じ例で，正規分布の代わりにt分布を使って平均値の区間推定をしてみましょう！

前回と同じく，US Household Income Statisticsのデータセットを使って米国内の地域別の世帯収入の平均値のデータを見ていきたいと思います．(各レコードは，”地域別の収入平均”になっていることに注意しましょう．)

まず前回同様，csvのデータをロードして母集団の平均値をみてみましょう．(この辺りはデータサイエンスのためのPython講座第11回に詳しく書いているので参考にしてください！)

import numpy as np
import pandas as pd

df = pd.read_csv('kaggle_income.csv', encoding="ISO-8859-1")
print(df['Mean'].mean())

import numpy as np

import pandas as pd

df = pd.read_csv('kaggle_income.csv', encoding="ISO-8859-1")

print(df['Mean'].mean())

66703.98604193568

1	66703.98604193568

約$66704であることがわかります．(今回は np.mean() ではなくてSeriesの .mean() を使ってみました．)

次に標本を作ります．今回も1000件をランダム抽出して標本平均を見てみましょう．

n=1000
sample_df = df.sample(n=n)
print(sample_df['Mean'].mean())

n=1000

sample_df = df.sample(n=n)

print(sample_df['Mean'].mean())

67102.57

67102.57

約$67103とでました．これは母集団の平均とはすこし異なりますね．(この数字は標本変動によりみなさんの実際の結果とは異なることに注意してください)

では，t分布を使って95%信頼区間を出してみましょう．これをやるには今まで通り stats.t.interval() を使えばOKです．このメソッドにalpha=0.95, loc=$\bar{x}$, scale=$\frac{s’}{\sqrt{n}}$, df=n-1を入れていきます．（前回の stats.norm.interval() の引数にdfを追加しただけですね）

from scipy import stats
sample_mean = sample_df['Mean'].mean()
sample_std = stats.tstd(sample_df['Mean'])
stats.t.interval(alpha=0.95, loc=sample_mean, scale=sample_std/np.sqrt(n), df=n-1)

from scipy import stats

sample_mean = sample_df['Mean'].mean()

sample_std = stats.tstd(sample_df['Mean'])

stats.t.interval(alpha=0.95, loc=sample_mean, scale=sample_std/np.sqrt(n), df=n-1)

(65189.2895147609, 69015.8504852391)

1	(65189.2895147609, 69015.8504852391)

t分布で区間推定をした結果「95%の確からしさで母集団の平均は$65189〜$69016の間にある」ことがわかりました．実際に母集団の平均は$67103なので今回の推定は当たっていることになります．(今回は不偏分散$s’^2$ではなくて標本標準偏差$s’$を stats.std() を使って計算してみました．ここでは n-1 で割った不偏分散の平方根の標準偏差を使うことに注意しましょう.例えば np.std() を使うと n-1 ではなくて n で割った時の標準偏差が計算されてしまうので， np.std() を使いたい場合は np.std(ddof=1) としてください)

では，t分布ではなく前回同様正規分布を使った場合の区間推定はどうなるのでしょうか？正規分布の区間推定は stats.norm.interval() を使えばOKです．(これは前回の記事でやった通りですね)

stats.norm.interval(alpha=0.95, loc=sample_mean, scale=sample_std/np.sqrt(n))

1	stats.norm.interval(alpha=0.95, loc=sample_mean, scale=sample_std/np.sqrt(n))

(65191.60755148405, 69013.53244851597)

1	(65191.60755148405, 69013.53244851597)

結果をみると，t分布の区間よりほんの少し狭くなってるのがわかると思います．これは，自由度999(1000-1)のt分布はほんの少しだけ正規分布より裾野が長いので，その分t分布では95%の区間が長くなっているわけです．

t分布を使うのか正規分布を使うのか

じゃぁ，t分布の結果と正規分布の結果，どっちが正しいの？

これはもちろん，近似を使わないt分布が正しいと言えます．

なので，もしPythonなどの統計ツールを使う場合はt分布を使って推定するのが◎です．

ただし，実際には多くの人が正規分布を使っています．標本の数が多ければt分布は標準正規分布に限りなく近くなる上に，計算上簡単になるからです．

個人的には，ある程度標本が大きければ(n>30くらい)正規分布でもいいと思います．(もちろんPythonのように労力が同じであればt分布のほうがベターかなと思いますが，そこまで気にする問題ではないと思います．)

まとめ

今回はt分布の解説とt分布を使った平均の区間推定を行いました．

t分布は統計(のみならず機械学習でも！！)の理論上さまざまなところで出てくるので是非今回の記事でt分布のイメージを掴んでおきましょう！

t分布は，平均$\bar{x}$の標本分布において，母集団の標準偏差$\sigma$の代わりに標本標準偏差$s’$を用いた場合の標準化後の平均$\bar{x}$が従う確率分布
t分布は自由度n-1を唯一のパラメータとする確率分布
自由度を大きくすると徐々に標準正規分布に近づく
t分布は標準正規分布に比べ裾野が長くなる(つまり標準正規分布と同じ区間だととりうる確率が低くなる．言い換えると同じ確率で区間をとったとき，t分布の方が区間が長くなる)
t分布を使った区間推定は stats.t.interval() に alpha (信頼係数), loc (標本平均), scale (標本平均の標準偏差), df (自由度)を渡すことで計算できる
標本が十分に大きければt分布でも標準正規分布でも結果はほとんど変わらない．