ポワソン分布を完全解説！正規分布や二項分布との関係は？【統計学入門20】

こんにちは，米国データサイエンティストのかめ(@usdatascientist)です．

Pythonで学ぶデータサイエンス入門：統計編第20回です! (もう20回か．．．統計学は文章が長くなるので記事数も多くなりそう．)

（追記）全16時間の統計学動画講座を公開しました！☆4.8の超高評価をいただいている講座です．こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください．

前回は最も基本的な確率分布である二項分布について紹介しました．今回の記事では二項分布を発展させた確率分布であるポワソン分布を紹介していきたいと思います！

端的にいうと，

ポワソン分布は「ある時間内に平均$\mu$回起こる事象がその時間内に$x$回起こる確率」

を分布で表したものになります．

言葉で表しても全然意味がわからないと思うので，これから超わかりやすく解説していきます！実世界にて直で使える素晴らしいツールなので是非押さえておきましょう！

1 ポワソン分布は二項分布の極限である
2 ポワソン分布をPythonを使って求めてみる
3 まとめ

ポワソン分布は二項分布の極限である

ポワソン分布は，数ある確率分布の中でもとりわけ有名で，現実問題にもよく応用される確率分布です．

例えば，1日に平均10回の交通事故が起こるとしましょう．今日交通事故が一回も起きない確率や，20回起きる確率をこのポワソン分布を使うことで求めることができます．

他にも例えば，平均100個に1個の割合で発生する不良品を200個ずつ箱に梱包したとき，1箱に不良品が入っていない確率や，5個入っている確率なんかを求めることができます．

ね？かなり実践的でしょ？

これを二項分布を基に考えてみましょう．

二項分布は，$n$回ある試行した時にある事象が確率$p$で起こるとして，その事象が実際に起こる回数$x$が従う確率分布でしたね.（詳しくは前回の記事参照）

ポワソン分布は，二項分布の$np$を一定にして，$n$を無限大に，$p$を限りなく小さくした極限で表すことができます．ここで，$np$を$\mu$と表記します．($\mu$ではなく$\lambda$を用いることも多いんですが，のちに紹介するscipyライブラリの実装に合わせて$\mu$を使います．)

どういうことかというと，例えば1日に平均5回起こる交通事故の例を考えてみましょう．

こんな風に，1日の時間軸に交通事故のタイミングをプロットしてみます．

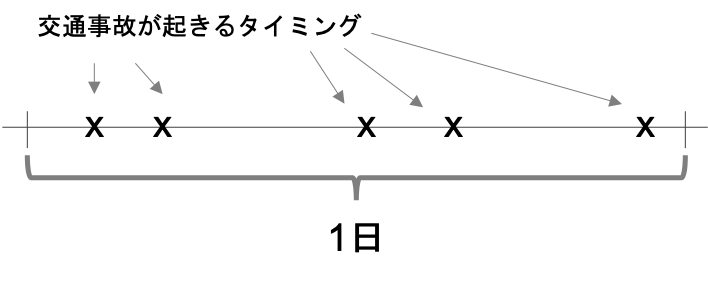
これを以下のように1日を非常に細かい単位に区切る，この区切った細かい一つ一つに対して「交通事故が起きた」「交通事故が起きてない」の二つの事象を割り当てることができます．

どういうことか．もう少しわかりやすく説明をすると，

例えば1日を1秒単位で区切ってみます．そうすると1日は24x60x60=86400秒なので1日を86400個に区切ったことになります．

この各1秒の間に「交通事故が起きた」「交通事故が起きていない」の二つの事象を割り当てることを考えると，これは二項分布で表すことができます．交通事故が起こる確率を$p$とし，1日に86400(=$n$)回試行して5(=$x$)回実際に交通事故が起きたと考えましょう

ここで，各1秒の間に交通事故が起こる確率(=$p$)は限りなく小さいですよね？

1日に5回起きるということは86400秒のうち5回しか起きないので，ある1秒に「交通事故が起きた」という事象を観察する確率は低いはずです．

交通事故は同時には起きないことを想定しています．「１秒間に二回起きてもおかしくないでしょ？」と思う人は，1秒ではなく0.001秒など，もっと細かく刻んでみてください．そうするとさらにその刻んだ間隔で交通事故を観察する確率はさらに小さくなります．

これは二項分布における$n$を無限大に，$p$を限りなく0にしたケースだと言えます．ここで，$\mu=np$とし，この$\mu$が一定になるように$n$を大きく，$p$を小さくしていくことを考えます．．

そうすると，ポワソン分布(Poisson Distribution)と呼ばれる離散確率分布になります．証明は省きますが，一応数式だけ載せておきますね．

$$P(x)=\frac{\mu^xe^{-\mu}}{x!}$$

このポワソン分布を使って，「ある時間内に平均$\mu$回起こる事象がその時間内に$x$回起こる確率」を求めることができます．

ポワソン分布はよく「時間」に対して使われますが，もちろん「時間」以外にも使えます．

先ほどあげた例以外にも，例えば１ページにタイプミスをする回数なんかもポワソン分布を使って求めることができます．

注意
よく「時間」が使われるのは，限りなく小さく区切ることができて，確率$p$ を限りなく0にすることができるからです．基本的には「”めったにおきない事象”を扱うときはポワソン分布が向いている」と思っておきましょう！

そしてこの$\mu$が大きくなると，正規分布に近づいていきます．これについてはまた次回の記事で紹介したいと思います！

ポワソン分布をPythonを使って求めてみる

前回の記事同様，今回も scipy.stats モジュールを使ってポワソン分布を使ってみましょう！

ポワソン分布は poisson を使えばOKです．

前回の記事では .rvs() 関数を使って，確率変数の値をサンプリングしましたが，今回は .pmf() 関数を使ってポワソン分布の描画をしたいと思います．

pmfはProbability Mass Function(確率質量関数)の略です．確率質量関数は，離散型確率変数が取る確率を対応させた関数のことで，連続型確率変数の確率密度関数(Probability Density Function:PDF)と対比関係にあるものです．

.pmf() 関数に mu 引数に$mu$, k 引数に回数を入れれば，その確率を求めることができます．

例えば，10分間に平均5回鳴るコールセンターで，1時間に40回電話が鳴る確率は$\mu=5\times\frac{60}{10}=30$，$k=40$とすればOKです．

$\mu$の求め方は，求めたい確率の単位時間(今回なら1時間)における平均の回数なので，今回は10分に平均5回ということは1時間に平均30回なので$\mu=30$です．

kとは何か
離散確率分布では，xは離散的な値を取るので，「確率変数$x$が$k$($k$=0, 1, 2,…, $k$)の時」という風に考えることができます．その場合，数式では$P(x=k)$のように表しますが，本ブログでは特に気にせず$P(x)$と表記してます)

それでは求めてみましょう．数式通りに計算した場合と比較して，値が同じであることを確認します．

from scipy.stats import poisson
import math
import numpy as np
mu = 30
k = 40
p1 = poisson.pmf(k=k, mu=mu)
#ポワソンの式を普通に求めてみる
p2 = (mu**k * np.e**(-mu))/math.factorial(k)
print(p1, p2)

from scipy.stats import poisson

import math

import numpy as np

mu = 30

k = 40

p1 = poisson.pmf(k=k, mu=mu)

#ポワソンの式を普通に求めてみる

p2 = (mu**k * np.e**(-mu))/math.factorial(k)

print(p1, p2)

0.013943463479967897 0.013943463479967761

1	0.013943463479967897 0.013943463479967761

scipy.stats.poisson を使ってケースと普通に数式通りに計算した値が同じになっているのがわかると思います．

0.0139…ということは，1.4%くらいしかないということです．これは大きいのでしょうか？

横軸にk=0, 1, 2, …., 50としてそれぞれのポワソン分布で得られた確率変数をplotしてみましょう．

import matplotlib.pyplot as plt
%matplotlib inline
x = np.arange(51)
plt.plot(x, poisson.pmf(k=x, mu=mu), 'bo')
plt.vlines(x, 0, poisson.pmf(k=x, mu=mu))
plt.xlabel("Nom. of calls wihtin a hour")
plt.ylabel("probability")

import matplotlib.pyplot as plt

%matplotlib inline

x = np.arange(51)

plt.plot(x, poisson.pmf(k=x, mu=mu), 'bo')

plt.vlines(x, 0, poisson.pmf(k=x, mu=mu))

plt.xlabel("Nom. of calls wihtin a hour")

plt.ylabel("probability")

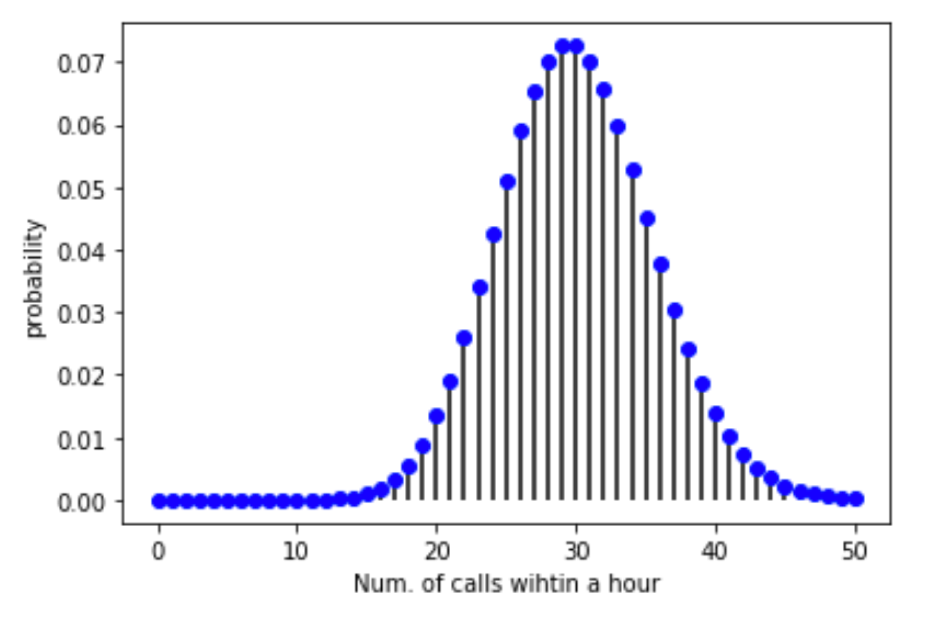
離散確率分布なので， plt.plot() の際に点と点を線で結ぶことはせず，今回は plt.vlines() を使ってx軸から点まで線を引きました．このあたりのPythonがあやしい人はこちらの記事を参考にしてください．また，「データサイエンスのためのPython動画講座」ではデータの可視化についてかなり詳しく扱っていますのでまだ受講していないかたは是非受講してください．

【公開初日で受講生1000人超え！】データサイエンスのためのPython動画講座を公開しました【全23時間…!!】

さて，先のplotをみると，一番確率が高いのが(当然)1時間に30回電話が鳴る時で，それでも確率は7%ちょいです．

この確率は“ちょうどその回数”電話が鳴るということなので，そこまで高くはならないんですね．

ポワソン分布のplotですが，なんだか正規分布に似てませんか？ mu の値を変えてplotしてみてください． mu を大きくしていくと正規分布の形に近くなっていくのがわかると思います．

以下のように．muにいくつか異なる値を入れたときのそれぞれのポワソン分布がどのような形になるのか見てみましょう

x = np.arange(20)
mu_list = [1, 3, 5, 10]
for idx, mu in enumerate(mu_list):
    plt.plot(x, poisson.pmf(k=x, mu=mu), 'o-', label='mu={}'.format(mu))
plt.legend()
plt.xlabel("Num. of calls wihtin a hour")
plt.ylabel("probability")

x = np.arange(20)

mu_list = [1, 3, 5, 10]

for idx, mu in enumerate(mu_list):

plt.plot(x, poisson.pmf(k=x, mu=mu), 'o-', label='mu={}'.format(mu))

plt.legend()

plt.xlabel("Num. of calls wihtin a hour")

plt.ylabel("probability")

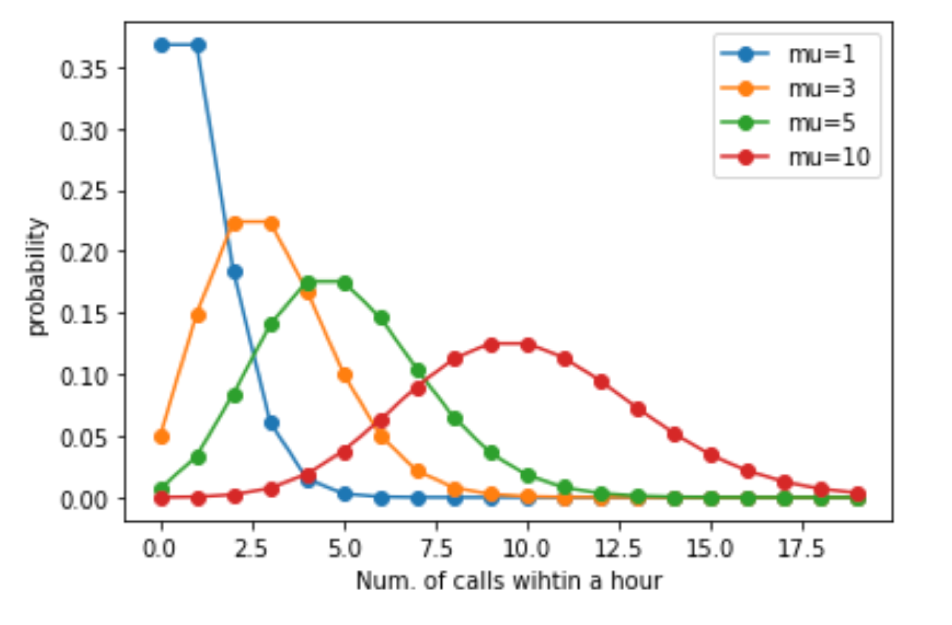
※わかりやすいように各点を線で結んでいますが，実際には離散的な値を取る離散分布であることに注意しましょう

まとめ

今回はポワソン分布を紹介しました．

ポワソン分布は実世界の問題によく適用される確率分布である．
ポワソン分布は二項定理の極限により定義される．$\mu=np$を一定にし，$n$を無限大に，$p$を限りなく小さくする．
ポワソン分布は「ある時間内に平均$\mu$回起こる事象がその時間内に$x$回起こる確率」を表している．(必ずしも「時間」である必要はない)
ポワソン分布を扱うには scipy.stats.poisson を使う
確率質量関数(PMF: Probability Mass Function)は，離散型確率変数が対応する確率を表した関数で，連続型確率変数における確率密度関数(PDF: Probability Density Function)との対比で覚えておく．
.pmf(k=, mu=) 関数を使って単位時間あたり平均 mu 回起こる事象が k 回観察される確率をポワソン分布から求める．