(追記)全16時間の統計学動画講座を公開しました!☆4.8の超高評価をいただいている講座です.こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください.
統計編も第10回まで来ました.まだまだ終わる気配はありません.
簡単に今までの流れを説明すると,第1回で記述統計と推測統計の話をし,今まで記述統計の指標を説明してきました.
代表値として平均(第2回),中央値と最頻値(第3回),散布度として範囲とIQRやQD(第4回),平均偏差からの分散および標準偏差(第5回),不偏分散(第6回)を紹介しました.(ここまででも結構盛り沢山でしたね)
これらは,1つの変数についての記述統計でしたよね?

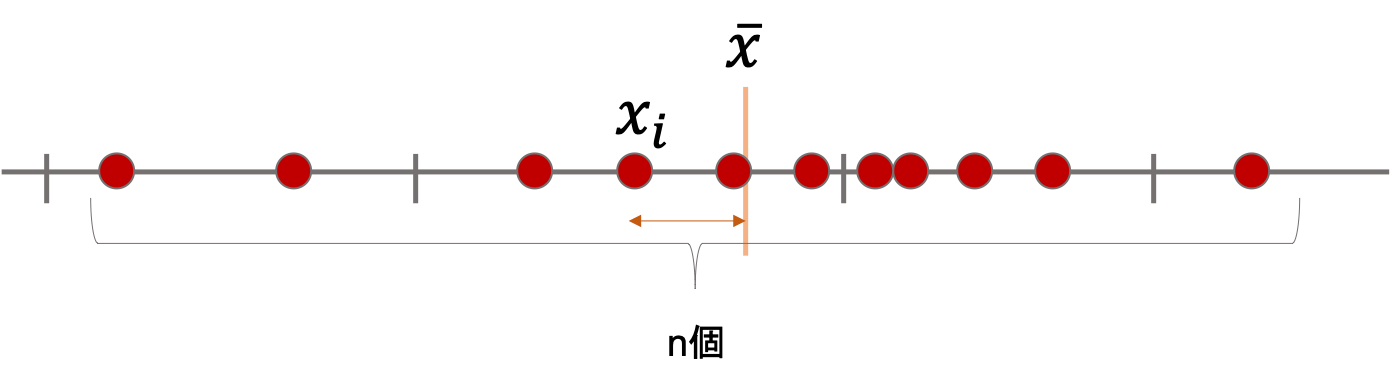
例えば,あるクラスでの英語の点数や,あるグループの身長など,1種類の変数についての平均や分散を議論していました.
↓こんな感じ

でも,実際のデータサイエンスでは当然,変数が1つだけということはあまりなく,複数の変数を扱うことになります.(例えば,体重と身長と年齢なら3つの変数ですね)
今回は,2変数における記述統計の指標である共分散について解説していきたいと思います!
2変数の関係といえば,「データサイエンスのためのPython講座」の第26回で扱った「相関」がすぐ頭に浮かぶと思います.相関は日常的にも使う単語なのでわかりやすいと思うんですが,この”相関を説明するのに“共分散”というものを使うので,今回の記事ではまずは共分散を解説します.”共分散”は馴染みのない響きで初学者がつまずくポイントでもあります.が,共分散はなんら難しくないので,是非今回の記事で覚えちゃってください!
目次
共分散は分散の2変数バージョン
“共分散”(covariance)という言葉ですが,”共”(co)と”分散”(variance)の2つの単語からできています.
“共”というのは,”共に”の”共”であることから,”2つのもの”を想定します.
“分散”は今まで扱っていた散布度の分散ですね.つまり,共分散は分散の2変数バージョンだと思っていただければいいです.
まずは普通の分散についておさらいしてみましょう.
$$s^2=\frac{1}{n}\sum^{n}_{i=1}{(x_i-\bar{x})^2}$$
上の式はこのようにして書くこともできますね.
$$s^2=\frac{1}{n}\sum^{n}_{i=1}{(x_i-\bar{x})(x_i-\bar{x})}$$
さて,もしこのデータが\(x\)のみならず\(y\)という変数を持っていたら...?
例えばこのデータは体重だけでなく,身長の値も持っていたら?当然以下のような図になると思います.
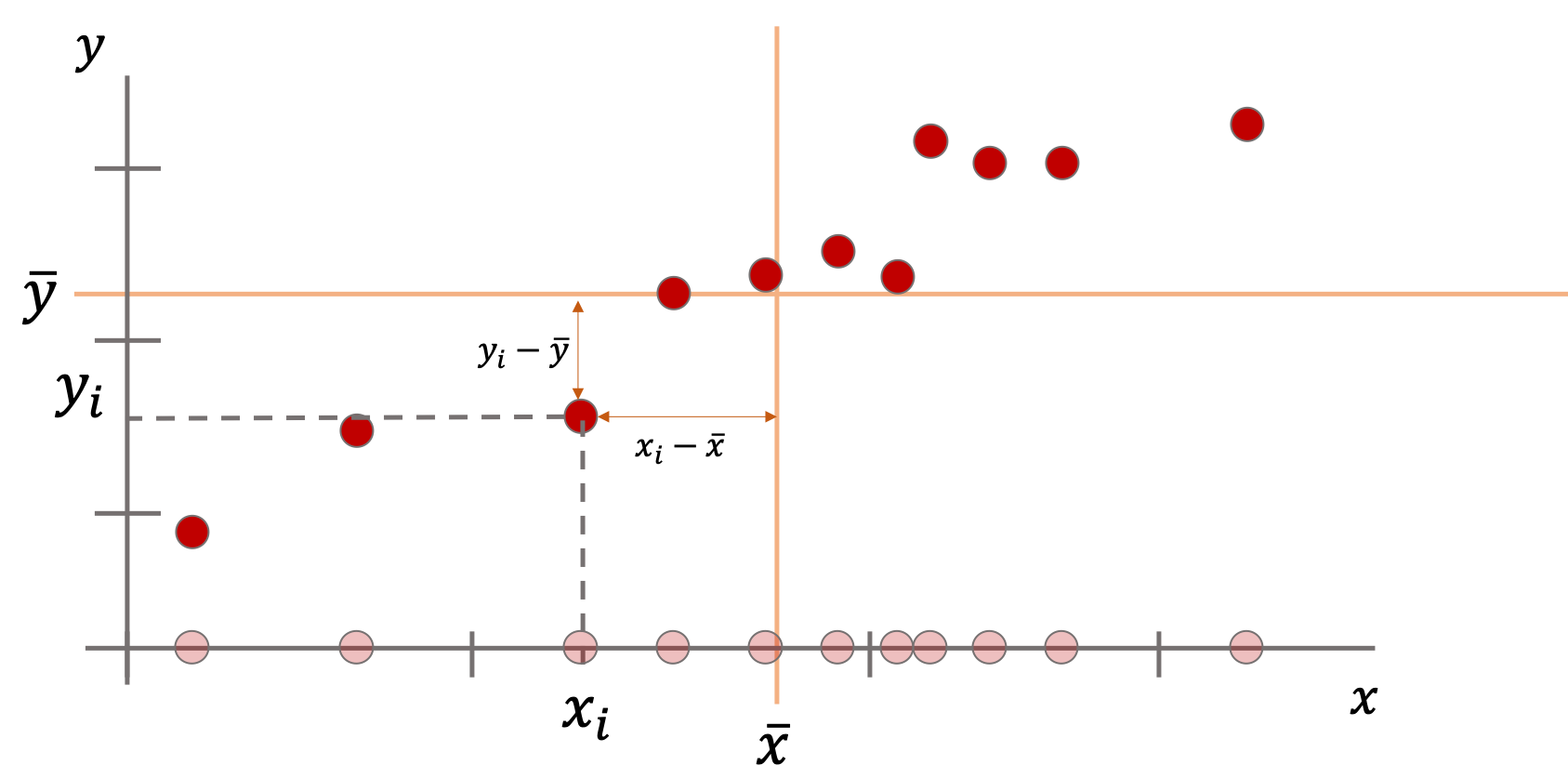
ここで,1変数の時は1つの平均(\(\bar{x}\))からの偏差だけをみていましたが,2つの変数(\(x, y\))があるので平均からの偏差も2種類(\((x_i-\bar{x}\))と\((y_i-\bar{y})\))あることがわかると思います.
これらそれぞれの偏差(\(x_i-\bar{x}\))と\((y_i-\bar{y}\))を掛けた値の平均を共分散(covariance)と呼び,通常\(s_{xy}\)であらわします.
$$s_{xy}=\frac{1}{n}\sum^{n}_{i=1}{(x_i-\bar{x})(y_i-\bar{y})}$$
共分散の定義だけみると「???」って感じですが,上述した普通の分散の式と,上記の2変数の図を見ればスッと入ってくるのではないでしょうか?
共分散は2変数の相関関係の指標

これが一番の疑問ですよね.なんとなーく分散の式から共分散を説明したけど,結局なんなの?と疑問を持ったと思います.
共分散は簡単にいうと,「2変数の相関関係を表すのに使われる指標」です.

いいえ.散らばりを表す指標はそれぞれの軸の”分散”を見ればOKです.以下の図をみてみてください.
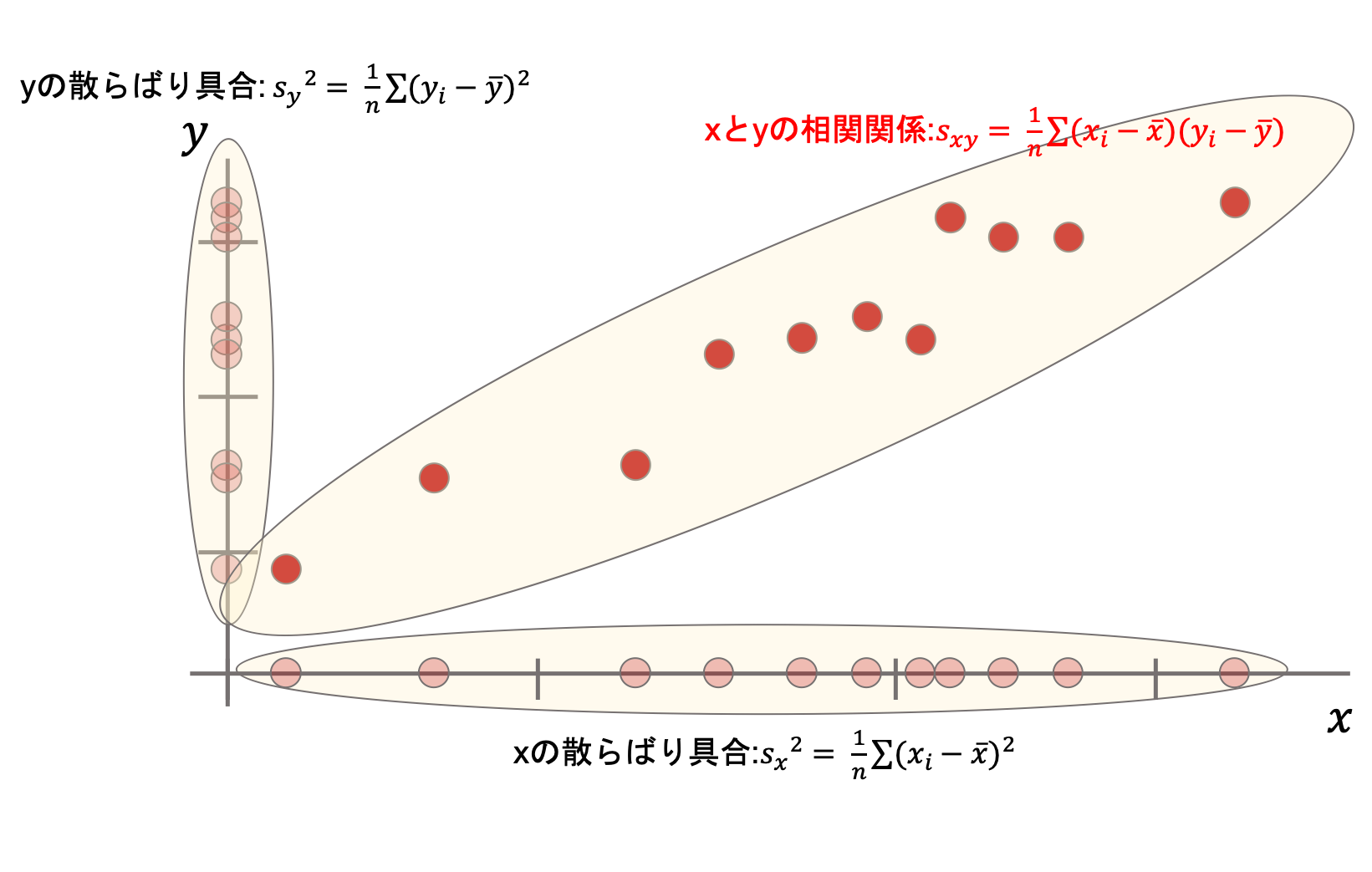
「どれくらい散らばっているか」は\(x\)と\(y\)の分散(\(s_x^2\)と\(s_y^2\))からそれぞれの軸での散らばり具合がわかります.
共分散でわかることは,「xとyがどういう関係にあるか」です.もう少し具体的にいうと「どういう相関関係にあるか」です.
例えば身長が高い人ほど体重が大きいとか,英語の点数が高い人ほど国語の点数が高いなどの傾向がある場合,これらの変数間は相関関係にあると言えます.(相関については「データサイエンスのためのPython講座」の第26回でも扱いました.)
日常的に使う単語なのでイメージしやすいと思います.
正の相関と負の相関と無相関
相関には正の相関と負の相関があります.ある値が大きいほどもう片方の値も大きい傾向にあるものは正の相関.逆にある値が大きいほどもう片方の値は小さい傾向にあるものは負の相関です.そして,ある値の大小ともう片方の値の大小が関係ないものは無相関と言います.
正の相関では共分散は正,負の相関では共分散は負,無相関では共分散は0になります.
ここで,\((x_i-\bar{x})(y_i-\bar{y})\)がどういう時に正になり,どういう時に負になるか考えてみましょう.
負になる場合は,\((x_i-\bar{x})\)か\((y_i-\bar{y})\)が負の時.つまり,\(x_i\)が\(\bar{x}\)よりも小さくて\(y_i\)が\(\bar{y}\)よりも大きい時,もしくはその逆です.正になる時は\((x_i-\bar{x})\)と\((y_i-\bar{y})\)が両方とも正の時もしくは負の時です.
これは先ほどの図の例でいうと,以下のように色分けすることができますね.
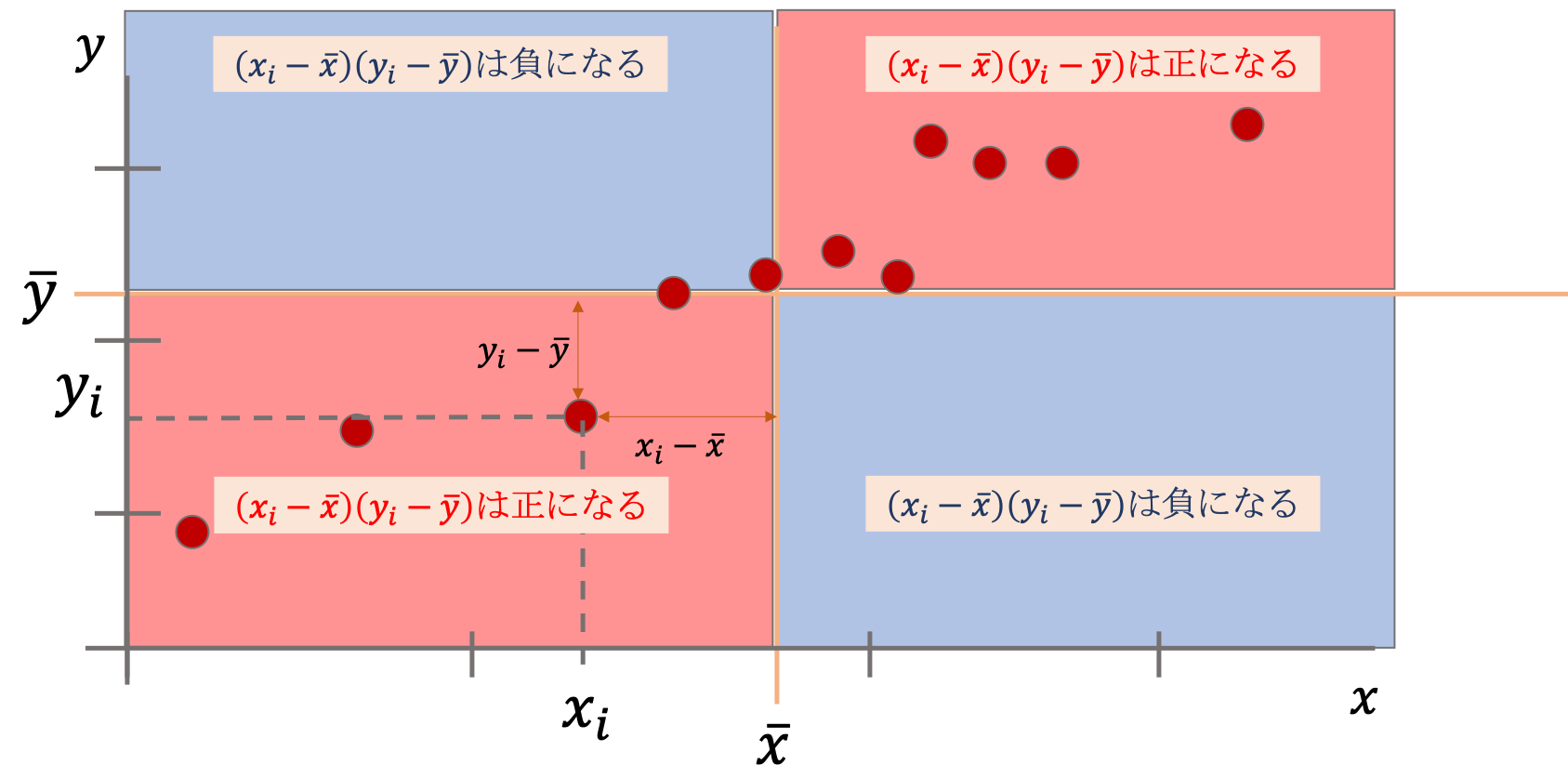
そして,共分散はこの\((x_i-\bar{x})(y_i-\bar{y})\)を全ての値において足し合わせていくのです.そして,最終的に上図の赤の部分が大きくなれば正,青の部分が大きくなれば負となることがわかると思います.
簡単ですよね!
では無相関の場合どうなるか?無相関ということはつまり,上の図で赤の部分と青の部分に同じだけデータが分布していることになり,\((x_i-\bar{x})(y_i-\bar{y})\)を全ての値において足し合わせるとプラスマイナス”0″となることがイメージできると思います.
無相関のときは共分散は0になります.
共分散が0だからといって必ずしも無相関とはならないことに注意してください.例えばデータが円状に分布する場合,共分散は0になる場合がありますが,「相関がない」とは言えませんよね?
この辺りはまた改めて取り上げたいと思います.
以上のことからも,共分散はまさに2変数間の相関関係を表していることがわかったと思います!
共分散がわかると,相関係数の式を解説することができます.次回は相関の強さを表すのに使用する相関係数について解説していきます!
Pythonで共分散を求めてみよう
NumPyやPandasの .cov() 関数を使って共分散を求めることができます.
今回はこんなデータでみてみましょう.(今までの図のデータに近い値です.)
|
1 2 3 4 5 6 7 8 9 10 |
import numpy as np import matplotlib.pyplot as plt import seaborn as sns %matplotlib inline weight = np.array([42, 46, 53, 56, 58, 61, 62, 63, 65, 67, 73]) height = np.array([138, 150, 152, 163, 164, 167, 165, 182, 180, 180, 183]) sns.scatterplot(weight, height) plt.xlabel('weight') plt.ylabel('height') |
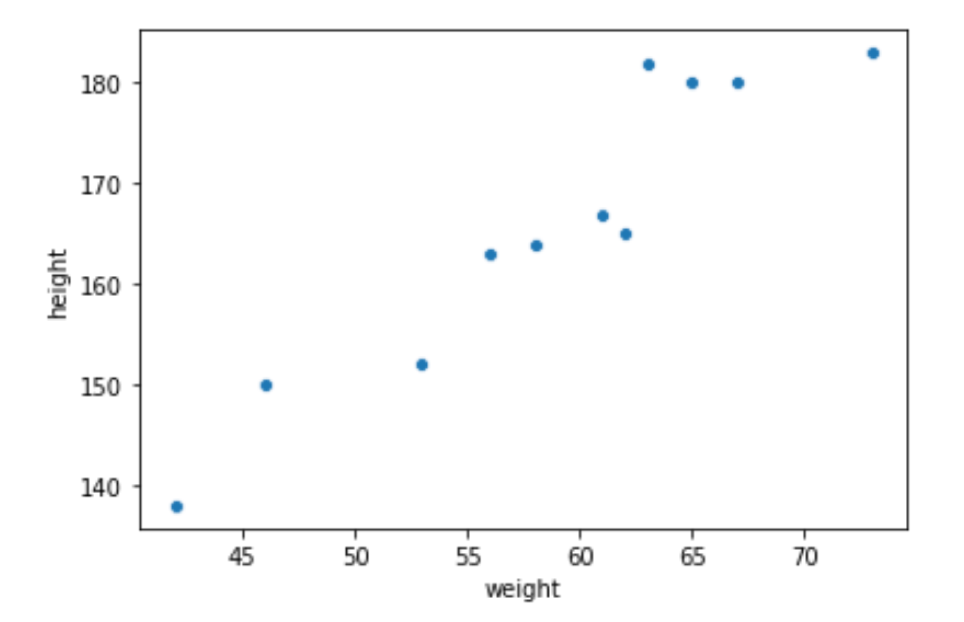
(データの可視化はデータサイエンスを学習する上で欠かせません.この辺りのライブラリの使い方に詳しくない方はこちらの回以降を進めてください.また,動画講座ではかなり詳しく&応用的なデータの可視化を扱っています.是非受講ください.)
さて,まずは np.cov() を使って共分散を求めてみましょう.
|
1 |
np.cov(weight, height) |
|
1 2 |
array([[ 82.81818182, 127.54545455], [127.54545455, 218.76363636]]) |
すると,おやおや,なにやら行列が返ってきましたね・・・
これは,分散共分散行列(variance-covariance matrix)(単に共分散行列とも)と呼ばれるものです.何も難しいことはありません.たとえば今回のweight, hightのような変数を仮に\(x_1\), \(x_2\), \(x_3\), .., \(x_i\)としましょう.
その時,共分散行列は以下のようになります.(第\(ii\)成分が\(s_i^2\), 第\(ij\)成分が\(s_{ij}\))
$$\left[ \begin{array}{rrrrr}
s_1^2 & s_{12} & \cdots & s_{1i}
\\ s_{21} & s_2^2 & \cdots & s_{2i}
\\ \cdot & \cdot & \cdots & \cdot
\\ s_{i1} & s_{i2} & \cdots & s_i^2
\end{array} \right]$$
また,NumPyでは共分散と分散が,分母がn-1になっている不偏共分散と不偏分散がデフォルトで返ってきます.なので,今回のweightとheightの例で返ってきた行列は以下のように読むことができます↓

つまり,分散と共分散が1つの行列であらわせれているので,分散共分散行列というんですね!
不偏推定量ではなく,ただたんに標本共分散と標本分散を算出したい場合は, bias=True を引数に渡してあげればOKです.
|
1 |
np.cov(weight, height, bias=True) |
|
1 2 |
array([[ 75.2892562 , 115.95041322], [115.95041322, 198.87603306]]) |
この場合,nで割っているので値が少し小さくなっていますね!このあたりの不偏推定量の説明はこちらの記事で詳しく解説しているので参考にしてください.
Pandasでも同様に以下のようにして分散共分散行列を求めることができます.
|
1 2 3 |
import pandas as pd df = pd.DataFrame({'weight':weight, 'height':height}) df |
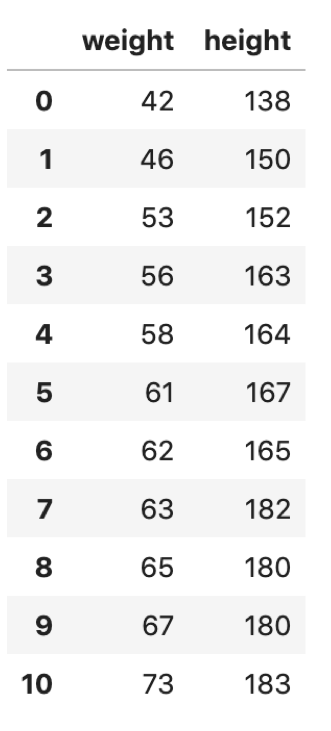
|
1 |
df.cov() |
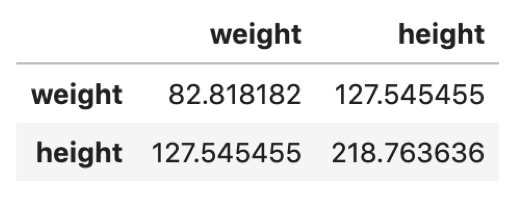
結果はDataFrameで返ってきます.DataFrameの方が俄然見やすいですね!このように,複数の変数が入ってくるとNumPyを使うよりDataFrameを使った方が圧倒的に扱いやすいです.今回は2つの変数でしたが,これが3つ4つと増えていくと,NumPyだと見にくいのでDataFrameを使っていきましょう!
DataFrameの .cov() もn-1で割った不偏分散と不偏共分散が返ってきます.
分散共分散行列は色々と使う場面があるのですが,今回の記事ではあくまでも「相関係数の導入に必要な共分散」として紹介するに留めます.
また今後の記事で詳しく分散共分散行列を扱いたいと思います.
まとめ
今回は2変数の記述統計として,2変数間の相関関係を表す共分散について紹介しました.
あまり馴染みのない名前なので初学者の人はこの辺りで統計が嫌になってしまうんですが,なにも難しくないことがわかったと思います.
- 共分散は分散の式の2変数バージョン(と考えると式も覚えやすい)
- 共分散は散らばり具合を表すのではなくて,2変数間の相関関係の指標として使われる.
- 2変数間の共分散は,その変数間に正の相関があるときは正,負の相関があるときは負,無相関の場合は0となる.
- 分散共分散行列は,各変数の分散と各変数間の共分散を行列で表したもの.
- np.cov() や df.cov() を使うことで,分散共分散行列を求めることができる.
- np.cov() や df.cov() はn-1で割った不偏共分散と不偏分散を返す.
今回の記事で,共分散についてはなんとなくわかっていただけたと思います.
冒頭にも触れた通り,共分散は相関関係の強さを表すのによく使われる相関係数を求めるのに使います.
正の相関の時に共分散が正になり,負の相関の時に負になり,無相関の時に0になるというのはわかりましたが,はたしてどのようにして相関の強さなどを求めればいいのでしょうか?
先ほどweightとheightの例で共分散が115.9とか127.5(不偏)という数字が出ましたが,これは一体どういう意味をなすのか?
その問いの答えとなるのが,次に説明する相関係数という指標です.
次回は,この共分散を使って相関係数という相関において一番重要な指標を解説していきます!
それでは!
(追記)次回書きました!