Pythonで平均値差の検定(t検定)をやってみる(等分散/非等分散)【統計学入門33】

こんにちは，米国データサイエンティストのかめ(@usdatascientist)です．

（追記）全16時間の統計学動画講座を公開しました！☆4.8の超高評価をいただいている講座です．こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください．

統計学入門第33回です．今回は前回の記事で紹介した平均値差の検定(t検定)を，Pythonで行ってみたいと思います！

理論知ってたって，使えなかったら意味ないですからね〜

今回もいつも通り，statsモジュールを使ってやっていきます．

それではやっていきましょう！

タイタニックデータを使ってt検定をやってみよう！

より実践的なコードを書いていきたいので，実際のデータセットを使ってt検定をやっていきます．

今回使うデータは，本ブログで何度も登場しているタイタニック号のデータセットです

タイタニック号のデータセットを使うにはKaggleへのアカウント作成が必要です．Kaggleのアカウント作成とデータセットのDLについては「データサイエンスのためのPython講座」の第11回を参考にしてください．

今回はタイタニック号の train.csv を使ってt検定をしていきます．

わかりやすいように， train.csv を titanic_train.csv に名前を変えてPythonコードからアクセスできるフォルダに移動させてください．(この辺りも第11回を参考にしてください)

まずはcsvファイルのデータをDataFrameに読み込む

これも本ブログで学習している方にとっては簡単かと思います．pandasの read_csv() を使ってDataFrameにロードしましょう．(このあたりの操作も「データサイエンスのためのPython講座」の第11回を参考にしてください．)

もし，Pythonの使い方やデータサイエンスに必要なPythonのライブラリの使い方がまだわかってないという方は是非僕のPython動画講座とデータサイエンスのためのPython動画講座を受講ください．

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
%matplotlib inline

df = pd.read_csv('titanic_train.csv')
df.head()

import numpy as np

import pandas as pd

import matplotlib.pyplot as plt

from scipy import stats

%matplotlib inline

df = pd.read_csv('titanic_train.csv')

df.head()

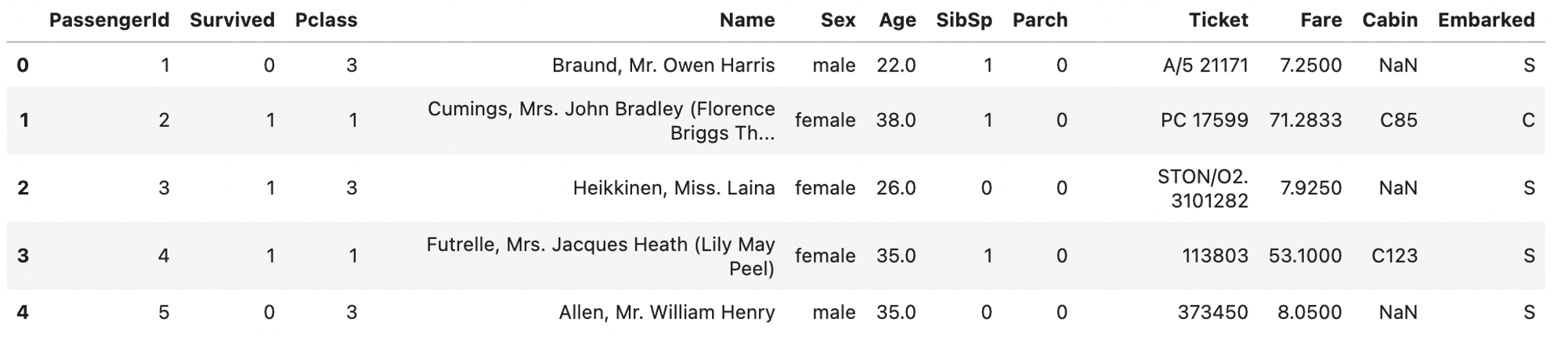
本データセットは，タイタニック号の乗客(train.csvは891人分)のプロファイル(年齢や性別，チケット代やクラスなど)や生死(Survived=0 or 1)の情報が入っています．

今回は，生存者と非生存者に分けて，それぞれの年齢の平均値に差があるのかを検定してみます．

おそらく生存者の方が平均年齢が低いのではないかなと予想します．(子供や若い人を優先して救命ボートに乗せていたと予想します．)

なので，「きっと生存者の方が若いよね？」という狙いのもと，「両者に差はない」という帰無仮説を立てるわけですね

両グループの平均値を見てみよう！

pd.read_csv() でcsvファイルを読み込んだら，いつも通り .describe() メソッドでそれぞれの統計値を見てみましょう．( .describe() についてはこちらの記事で紹介しています．)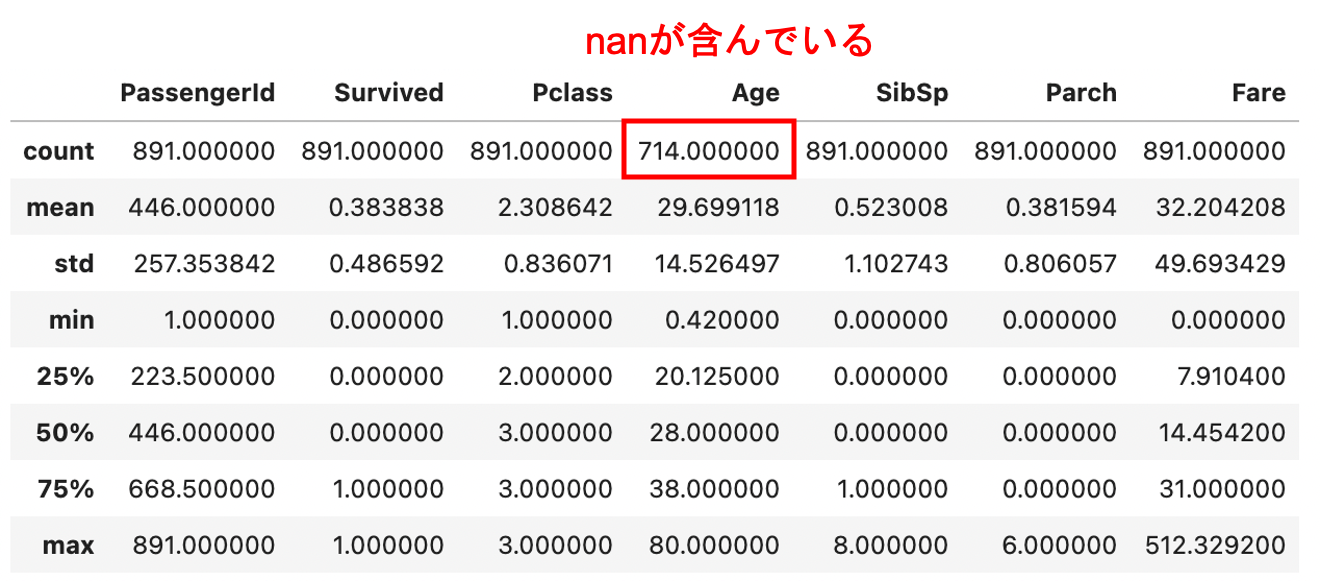

Ageのカウントを見ると，714レコードしかありません(他のカラムのcountは714より多いです．)

これは，nan(Not A Number: つまり空白)を含んでいることが原因です(これについてもこちらの記事で紹介しましたね．)

つまりいくつかの乗客はAgeの情報を持っていないということです．(このような値のことを欠損値と呼びます．Pandasでの欠損値の処理についてはこちらの記事に書いています．)

欠損値をどう扱うかは色々とやり方があるんですが，今回はひとまずnanのレコードを除外して検定します．

nanを含むレコードを除外するには .dropna() を実行すればOKです．.dropna()についてはこちらの記事でも紹介しています．

df = df.dropna()

1	df = df.dropna()

それでは，生存者とそうでない人のグループに分けましょう．これは，フィルタ処理をすればOKですね．

ages1 = df[df['Survived']==1]['Age']
ages2 = df[df['Survived']==0]['Age']

1 2	ages1 = df[df['Survived']==1]['Age'] ages2 = df[df['Survived']==0]['Age']

この辺りの処理がわからない方は是非データサイエンスのPython動画講座を受講ください．(コード一つ一つを調べるより，一度体系的に学習した方が早いです．)

それぞれの平均値を見てみると

print(ages1.mean(), ages2.mean())

1	print(ages1.mean(), ages2.mean())

32.905853658536586 41.35

1	32.905853658536586 41.35

となり，生存者の方が平均値が10歳ほど若いことがわかります．ふむふむ，予想通りですね！！

でも，これに対して「いやいや，そんなのたまたま今回取ってきた714名のデータがそうだっただけで，タイタニック号全体の乗客を調べたらそうはならないよ！」という人がいたとします(どんな状況w)

そういう人たちに対して，平均値差の検定結果を見せつけてやりましょう．

statsモジュールのttest_ind()を使ってt検定を行う

Pythonを使ってのt検定はやはりめちゃくちゃ簡単です．

statsモジュールのttest_ind()という関数があるのでそれを使います．indというのは，independentという意味で，独立した2群の平均値差の検定の場合にこの関数を使います．

今回の例は，二つのグループに対応はありません．（それぞれの値が同じ人の値でもないですしね．）なので独立した2群の平均値差を実行すればOKです．

ttest_ind()の引数として主には以下の４つを覚えておきましょう．

a, b: それぞれの標本の実際のデータをリストやnumpy arrayにしたもの
equal_var: booleanで，二つの母集団の分散が等しいとすればTrue，そうでなければFalse.デフォルトはTrueで，Falseの場合はウェルチのt検定というより高度な検定が実行される．
alternative: 両側検定だったら "two-sided" ,片側検定の場合は "less" か "greater" を指定する．対立仮説を「引数aの平均値<引数bの平均値」とするなら "less" , 「引数aの平均値>引数bの平均値」とするなら "greater" ． alternative 引数は，versionが1.6.0以上である必要があります．引数をセットできない人は pip install --upgrade scipy などでアップデートしてみましょう

さて，それでは早速やってみましょう！

今回は「生存者グループの方が平均年齢が低いはず」というのを狙って検定をするので，対立仮説は「生存者の平均年齢<非生存者の平均年齢」とし，片側検定をすればOKです．（そのため，ttest_ind()の alternative 引数には "less" を指定すればOKです．）

stats.ttest_ind(ages1, ages2, alternative='less')

1	stats.ttest_ind(ages1, ages2, alternative='less')

Ttest_indResult(statistic=-3.53435125095576, pvalue=0.0002594751653940836)

1	Ttest_indResult(statistic=-3.53435125095576, pvalue=0.0002594751653940836)

戻り値は二つ．検定統計量tの値とp値が返ってきます．(p値については第28回で説明してますね)

今回の結果はt=-3.53,p=0.00026です．p値はかなり低いですね．有意水準を5%とするとp値は<0.05なので，余裕で帰無仮説「生存者と非生存者で年齢の平均値に差はない」を棄却でき，対立仮説「生存者の平均年齢<非生存者の平均年齢」を成立させることができます．

Python使えばめちゃくちゃ簡単じゃん．．．

実際に検定統計量を計算してみる

前回の記事に書いた大標本の場合の正規分布に近似した検定統計量z

$$z=\frac{\bar{x}_1-\bar{x}_2}{\sqrt{\frac{{{s’}_1}^2}{n_1}+\frac{{{s’}_2}^2}{n_2}}}$$

および

小標本の場合の検定統計量t

$$t=\frac{\bar{x}_1-\bar{x}_2-(\mu_1-\mu_2)}{\sqrt{\frac{(n_1-1){{s’}_1}^2+(n_2-1){{s’}_2}^2}{n_1+n_2-2}}\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}=\frac{\bar{x}_1-\bar{x}_2-(\mu_1-\mu_2)}{\hat{\sigma}}$$

をそれぞれ計算してみましょう．

n1 = len(ages1)
n2 = len(ages2)
mean1 = ages1.mean()
mean2 = ages2.mean()
var1 = stats.tvar(ages1)
var2 = stats.tvar(ages2)
# 標準正規分布のzの式
z = (mean1 - mean2) / np.sqrt(var1/n1 + var2/n2)
print(f'z: {z}')
# t分布のtの式
t = (mean1 - mean2) / (np.sqrt(((n1-1)*var1 + (n2-1)*var2)/(n1 + n2 -2)) * np.sqrt(1/n1 + 1/n2))
print(f't: {t}')

n1 = len(ages1)

n2 = len(ages2)

mean1 = ages1.mean()

mean2 = ages2.mean()

var1 = stats.tvar(ages1)

var2 = stats.tvar(ages2)

# 標準正規分布のzの式

z = (mean1 - mean2) / np.sqrt(var1/n1 + var2/n2)

print(f'z: {z}')

# t分布のtの式

t = (mean1 - mean2) / (np.sqrt(((n1-1)*var1 + (n2-1)*var2)/(n1 + n2 -2)) * np.sqrt(1/n1 + 1/n2))

print(f't: {t}')

z: -3.4671799996491983
t: -3.5343512509557606

1 2	z: -3.4671799996491983 t: -3.5343512509557606

不偏分散は stats.tvar() を使えばいいんでしたね．(第5回参照)(z値とt値には少し差がありますね．これについてはまた後ほど述べます)

t値の値をみると，先ほどの ttest_ind() で計算した統計量と同じ値になっているのがわかると思います．

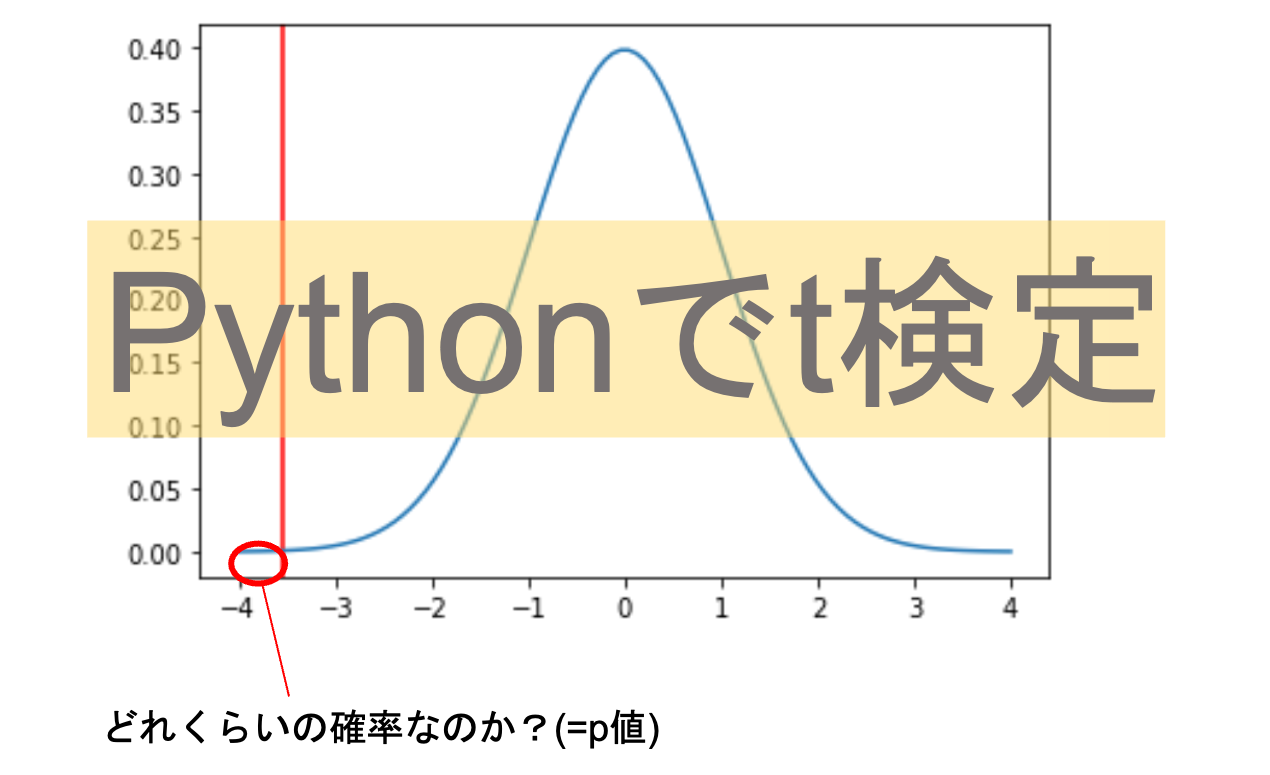
このt値の確率分布は，自由度$n_1+n_2-2$のt分布です．つまりこのt値が自由度$n_1+n_2-2$のt分布において，どれくらいの確率で得られる値なのかがp値になるわけです．

ttest_ind() の結果，p値は0.00026となっていますが，実際に自由度$n_1+n_2-2$のt分布において，このt値がどれくらいの確率で得られるかを stats.t を使ってみてみましょう．

x = np.linspace(-4, 4, 100)
y = stats.t.pdf(x, df=n1+n2-2)
plt.axvline(t, c='r')
plt.plot(x, y)

x = np.linspace(-4, 4, 100)

y = stats.t.pdf(x, df=n1+n2-2)

plt.axvline(t, c='r')

plt.plot(x, y)

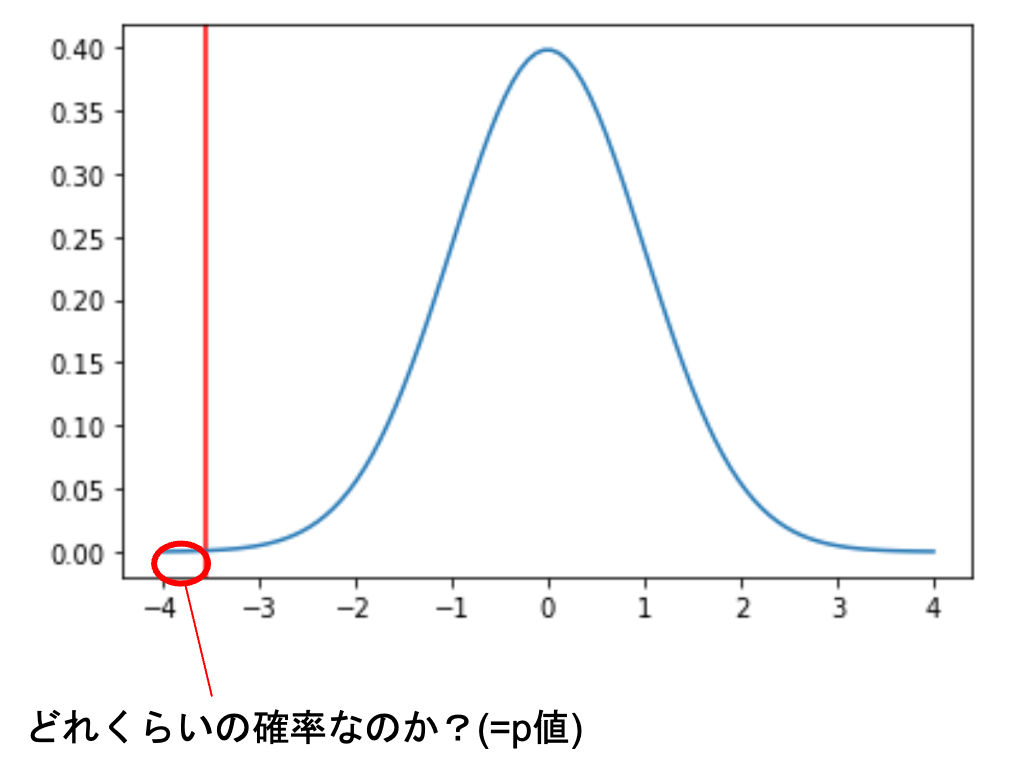
これには， .cdf() というメソッドを使って求めることができます．CDFというのは，Cumulative Density Functionの略で，日本語では累積分布関数と言います．

“cumulative”(累積)という単語から想像できるように，指定した値(x軸)におけるその確率密度の累積の値（つまり確率関数の下の面積=確率）を計算する関数です．

stats.t.cdf(t, n1+n2-2)

1	stats.t.cdf(t, n1+n2-2)

0.0002594751653940836

1	0.0002594751653940836

この値はttest_ind()の結果のp値と同じであることがわかります．

このことからも，ttest_ind()がt値を計算していて，自由度$n_1+n_2-2$のt分布におけるp値を計算しているのがわかるかと思います．

２つの母集団が等分散性を持たない場合

t検定は，小標本の場合二つの母集団の分散が等しいと仮定しています．

補足
分散が等しいことを「等分散である」や「等分散性」といったりし，逆に分散が等しいと言えない場合，「非等分散」や「分散の不均一性」と言ったりします．

今回の生存者と非生存者の年齢の分散は等しいといえるの？

今回は，２つの母集団が等分散であると仮定してt検定をしましたが，本当に等しいと言えるのでしょうか？まずはそこを確認する必要はないのでしょうか？

母集団の分散が等しいかをみるのは難しそうですが，少なくとも両標本の分散を確認することはできるはず！ということで見てみると(不偏分散( stats.tvar() )は先ほど計算済みですね)

print(var1, var2)

1	print(var1, var2)

221.71546053578567 247.73135593220334

1	221.71546053578567 247.73135593220334

生存者の年齢の不偏分散は約222，非生存者の不偏分散は約247と，んー，同じとは言えなさそうな気もしますね．

実は，等分散性を検定することもできます．これについてはまた次回の記事で書いていこうと思います．

なので，t検定を行う前に等分散性の検定をして，等分散性が言えたらt検定をして，言えなかったらウェルチのt検定（等分散ではなかった場合のt検定）をするというのが一般的です．

補足
最近では，等分散性の検定をせずに，分散がどうであろうとウェルチのt検定をするという人も多いです．このあたりについては，また機会があったら記事にしたいと思います．

等分散でなければttest_ind()の equal_var 引数を False にすればいいんだね！

その通り！そうするとウェルチのt検定という，非等分散をもつ可能性がある２つの標本におけるt検定を実行してくれます．(理論の説明についてはまた機会があったら記事にしたいと思います．)

stats.ttest_ind(ages1, ages2, alternative='less', equal_var=False)

1	stats.ttest_ind(ages1, ages2, alternative='less', equal_var=False)

Ttest_indResult(statistic=-3.4671799996491983, pvalue=0.00037406721468806855)

1	Ttest_indResult(statistic=-3.4671799996491983, pvalue=0.00037406721468806855)

すると，検定統計量の値が-3.467, p値が0.00037という結果になりました．

この検定統計量は，先ほど計算した「大標本の場合の正規分布に近似した場合の検定統計量z」と同じですね．

これは，標本が大きければそもそも非等分散でも検定統計量zを求めればいいということに一致します．今回のケースは標本のサイズが714ということで十分多く，ウェルチのt検定を実行すると，等分散性を考慮することなく正規分布に近似できたので結果検定統計量zと一致したわけです．

小標本で２つの母集団が正規分布ではなさそうな場合

今回の例は大標本のケースなので，中心極限定理(第25回)により母集団が正規分布でなくても問題なく検定統計量の標本分布は標準正規分布に近似できます．(前回の記事参照)

しかし，小標本の場合，t検定を行うには等分散性および母集団が正規分布である必要があります．

もし母集団が正規分布と言えなかったら，t検定を行って正しく検定をすることはできません．これはウェルチのt検定も同様です．

その場合，また別の検定が必要になってきます．これについてはまた別途記事を書いていこうかと思います．(統計学習入門後編にでもしようかな・・・)

補足
大体25~30個ほど標本がとれれば，大標本として標準正規分布を使って検定することができると言われています．

まとめ

Pythonでt検定をするには stats.ttest_ind() を使用する
等分散性が言えない場合は， equai_var=False としウェルチのt検定を行う
大標本であれば，検定統計量tでなく検定統計量zを使えばいいので（特に等分散性が言えない場合は） equai_var=Falseとし，普通のt検定ではなくウェルチのt検定を行えばOK
.cdf() メソッドを使って累積分布関数(CDF)の値を取得することができる．

つまり，大標本であれば等分散性は意識する必要なく， equal_var=False としてウェルチのt検定を行ってよいということ(結果，統計検定量zになる)．小標本であれば，等分散性の検定(次回説明)をしてからt検定を行うか， equal_var=False としてウェルチのt検定を行えばOKです．

次回は二つの母集団が同じ分散なのかどうかを検定する，等分散性の検定の解説をしていきます！

それでは！

追記)次回の記事書きました