相関係数をわかりやすく解説【統計学入門11】

（追記）全16時間の統計学動画講座を公開しました！☆4.8の超高評価をいただいている講座です．こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください．

Pythonで学ぶデータサイエンス入門：統計編第11回です．

前回の記事で２変数間の相関関係を表す指標として共分散を紹介しました．

共分散を見て，１つ疑問に思いませんでしたか？共分散は「２変数間の相関関係を表す指標であり，正の相関があれば正，負の相関があれば負，無相関であれば0になる」のはわかったけれども，計算した共分散の値をどう解釈していいか，悩みますよね？

前回の記事で計算したweightとheightの共分散が115っていわれて，それが高いのか低いのか，相関が強いのか弱いのかわかりません．

そもそもweightとheightは[kg]と[cm]で単位も違くて標準化もしてません．

共分散が取りうる値をある値の範囲を“標準化”することができたら，その値を使って比較することができますよね？

そこででてくるのが相関係数と呼ばれるものです．こちらの記事でも取り上げましたが，今回の記事できちんと解説したいと思います．

まずは共分散の取りうる値を考えてみましょう！

相関関係が最大のとき，変数は直線に並ぶ

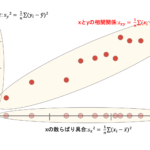
ある２つの変数間の相関関係が最大になるケースを考えましょう．

相関関係が最大ということは，片方の値が決まれば必然的にもう片方の値が決まるということです．以下のようにデータが一直線にならんだとき，完全な正の相関があると言えます．このとき，共分散は最大になります．

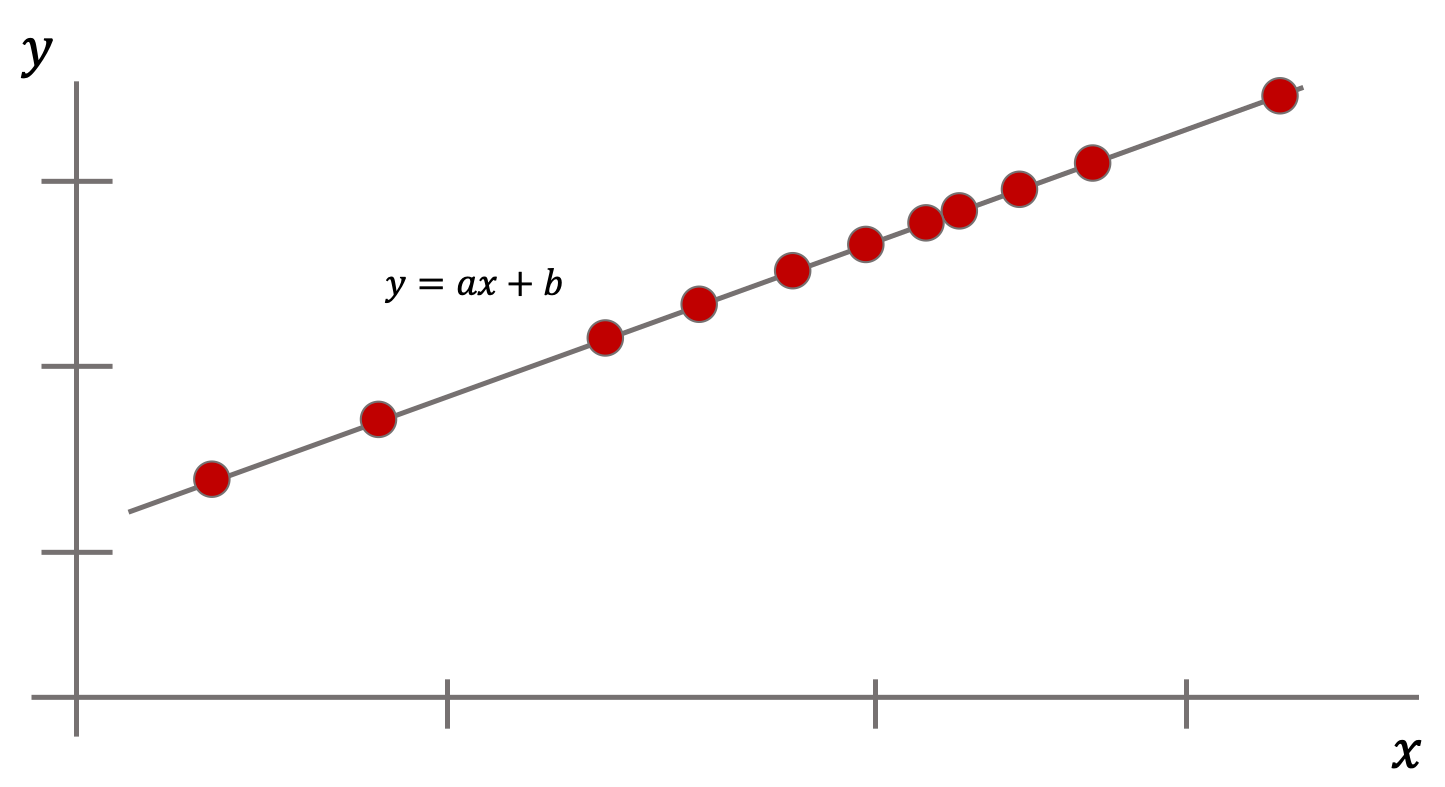
さて，完全な正の相関があるとき，共分散はどのような値をとるのかみてみましょう．仮に上図の直線が\(y=ax+b\)とすると，共分散の式はどのようになるでしょうか？

ここで，\(y\)は\(x\)から\(y=ax+b\)という線形変換されているわけですが，このように線形変換された場合，標準偏差\(s_y\)は\(as_x\)となります．全ての値がa倍されたら標準偏差もa倍されるわけです．ただの平行移動(\(y=ax+b\)の\(b\)の部分)は，標準偏差には影響しません．全ての値に+bされたとしても，値のばらつき具合は変わらないですもんね？

つまり，上記の式\(as_x^2\)は\(\frac{s_y}{s_x}s_x^2=s_xs_y\)となり,完全な正の相関のとき，

$$s_{xy}=s_xs_y$$

となることがわかると思います．

これと同様に完全な負の相関の時，仮に直線の式を\(y=-ax+b\)とすると\(a\)が負になることから

$$s_{xy}=-s_xs_y$$

となることがわかると思います．

つまり，共分散\(s_{xy}\)は\(-s_xs_y\)から\(s_xs_y\)の値を取るということですね！

$$-s_xs_y\leq s_{xy}\leq s_xs_y$$

これが相関係数だ！

$$-s_xs_y\leq s_{xy}\leq s_xs_y$$

これだと値の尺度によって共分散の取りうる値がまちまちなので，共分散同士で値を比較するのは難しい．

そこで，それぞれの辺に\(\frac{1}{s_xs_y}\)を掛けて取りうる値を-1〜1にします．

$$-1\leq\frac{s_{xy}}{s_xs_y}\leq1$$

この\(\frac{s_{xy}}{s_xs_y}\)こそが相関係数(correlation coefficient)と呼ばれる指標です．共分散で問題だった「とりうる値が値の尺度によってまちまち」という問題を解決した，相関関係を表すのに最も使われる指標です！

相関係数は-1から1までの値を取り，完全な正の相関のときに1, 完全な負の相関のときに-1になり，無相関のときに0になります．

一般に相関係数は\(r\)を用いて表され，変数xとyの相関係数は

$$r=\frac{s_{xy}}{s_xs_y}$$

となります．

Pythonで相関係数を求めてみよう！

それでは，いつものようにPythonを使って相関係数を求めてみましょう！

まずはNumPyの .corrcoef() 関数を使って相関係数を求めます．

前回の記事と同じndarrayを例にしています．

おや，，，？今回も行列が返ってきましたね． corrcoef() 関数は，相関行列(correlation matrix)というものを返します．

相関行列についてはこちらの記事でも紹介しましたね．読み方は以下のようになります．

同じ値同士の相関係数は当然1になるのと，変数を入れ替えてもその変数間の相関係数は同じなので，相関行列は対角成分が1の対称行列になるんですね！

実際の業務では，Pandasを使って相関行列(相関表)を作ることがほとんどなので，そのやり方をもう一度おさらいしておきましょう(「データサイエンスのためのPython講座」の第26回でやりましたね)

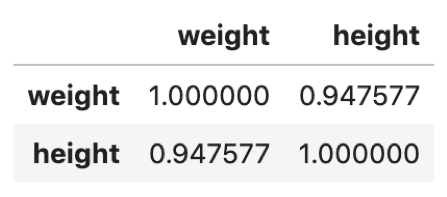
第26回で紹介した通り，Heatmapと組み合わせることが多いので復習も兼ねて紹介しておきます．(もちろん，変数が２つしかない場合はHeatmapは不要ですが，実際の業務ではもっと多くの変数間の相関をみることになるので)

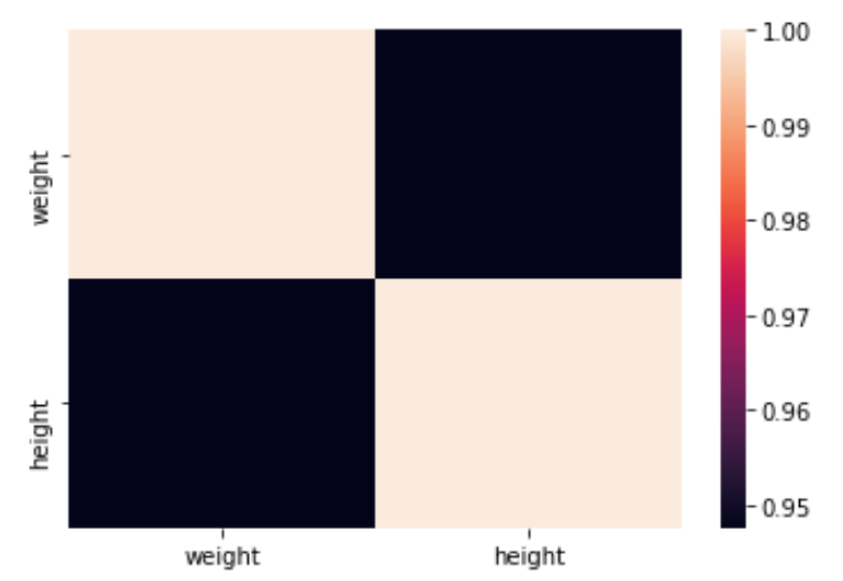
こんな感じですね．データサイエンスに必要なPythonの知識がない！っていう人は，是非こちらの動画講座で学習してください．23時間以上もの動画講座で，星4.7という超高評価講座になってますので，絶対に有益なはず．

【公開初日で受講生1000人超え！】データサイエンスのためのPython動画講座を公開しました【全23時間…!!】

まとめ

今回は相関関係の強さを表す最も重要な指標となる“相関係数”を紹介しました．

• 相関係数は-1から1の値をとるもので，変数間の相関の強さを表すのに最も使われる指標
• 相関係数は「変数間の共分散を各変数の標準偏差の積で割った値」で，すなわち\(\frac{s_{xy}}{s_xs_y}\)で定義され，\(r\)で表すのが一般的
• 相関行列(相関表)は各変数間の相関を表示したもの．対角成分が1の対称行列になる．
• NumPyの .corrcoef() やPandasの .corr() 関数では相関行列が返ってくる．

前回の共分散の説明と合わせて見ていただければ，きちんと理解できたのではないでしょうか？

実際に相関係数を見る機会は多いです．特にこちらの記事で紹介したように，ひとまず変数同士の相関係数をバーっとみたりします．

例えば機械学習でなにかモデルを学習させる場合，変数間の相関が高いものは片方の変数を学習から外したりします．(この辺りはまた機械学習の講座で解説します)

定義はわかったけどいまいち扱いがわからない，という人も多いと思います．次回はもっと「相関係数」について詳しく見ていきたいと思います！

それでは！

(追記)次回の記事書きました！相関係数の押さえておくべき３点について書きました．こちらも非常に重要な内容になってきますので，きちんと押さえておきましょう！

これだけは知っておいた方がいい相関係数のポイント3つ【統計学入門12】