これだけは知っておいた方がいい相関係数のポイント3つ【統計学入門12】

こんにちは，米国データサイエンティストのかめ(@usdatascientist)です．

（追記）全16時間の統計学動画講座を公開しました！☆4.8の超高評価をいただいている講座です．こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください．

Pythonで学ぶデータサイエンス入門：統計編第12回です．

今回も前回に引き続き相関係数について書いていきます．

相関係数は，変数間の相関関係の強さを表す指標として使えるという話は前回の記事でしました．

今回はこの相関係数のポイント(というか注意点?)を3つ挙げ，それぞれ解説していきたいと思います．

強い相関，弱い相関の基準(相関係数がいくつなら強い相関だと言えるの？)
相関係数だけをみるのは危険？散布図も合わせて見ておこう
相関関係と因果関係は区別して考えよう

それでは，１つずつ見ていきましょう！！今回の記事の内容は今後データサイエンスをする上で非常に重要かつ基本的な考え方になるので，是非きちんと押さえておきましょう！

知っておくと便利．相関の大小の基準

相関係数は-1~1に収まるので標準化されていて確かに使いやすいんですが，

それでもまだ，相関係数がいくつだったら強い相関なのか，いまいち説明していませんでした．

結論からいうと，これに明確な基準はありません．さらにいうと，その基準はデータの種類や分野によっても変わってくると思います．

えーでもなにか参考になる値はあるでしょ！？

という人のために，一般的に言われている基準値をここでは紹介します．

だいたい相関係数(の絶対値)が0.7を超えたら相関は強いと言っていいでしょう．0.2を下回るようなら相関はほぼないと思っていいと思います．

これらの値が，散布図でみるとどれくらいなのかPythonを使って表示してみましょう！

まずは任意の相関係数に対してランダムなデータセットを生成するプログラムを書きます．↓な感じで作ることができます．

import numpy as np
def generate_values(r=0.5, num=1000):
    
    # 値を標準正規分布からランダムで作成
    a = np.random.randn(num)
    # 誤差項1 'a'に誤差項1を加えたものをxとする
    e1 = np.random.randn(num)
    # 誤差項2　'a'に誤差項2を加えたものをyとする
    e2 = np.random.randn(num)
    # 相関係数が負の場合，負の平方根になってしまうので，xの式を負にする
    if r < 0:
        r = -r
        x = -np.sqrt(r)*a - np.sqrt(1-r)*e1
    else:
        x = np.sqrt(r)*a + np.sqrt(1-r)*e1
    y = np.sqrt(r)*a + np.sqrt(1-r)*e2
    # 相関行列からxとyの相関係数を取得
    actual_r = np.corrcoef(x, y)[0][1]
    
    return x, y, actual_r

import numpy as np

def generate_values(r=0.5, num=1000):

# 値を標準正規分布からランダムで作成

a = np.random.randn(num)

# 誤差項1 'a'に誤差項1を加えたものをxとする

e1 = np.random.randn(num)

# 誤差項2　'a'に誤差項2を加えたものをyとする

e2 = np.random.randn(num)

# 相関係数が負の場合，負の平方根になってしまうので，xの式を負にする

if r < 0:

r = -r

x = -np.sqrt(r)*a - np.sqrt(1-r)*e1

else:

x = np.sqrt(r)*a + np.sqrt(1-r)*e1

y = np.sqrt(r)*a + np.sqrt(1-r)*e2

# 相関行列からxとyの相関係数を取得

actual_r = np.corrcoef(x, y)[0][1]

return x, y, actual_r

np.random.randn() はこちらの記事でやりましたね．標準正規分布から値をランダムに生成する関数です． np.sqrt() は平方根をとります．

なぜ np.sqrt(r)*a + np.sqrt(1-r)*e1 のような式で生成できるのかについては，ここでは説明しません．実際の業務でこのような任意の相関係数からランダムな値を生成することなんてない(と思う)ので，このようなプログラムを書くこともないと思います．

ここでは”参考までに”コードを公開するに留め，興味がある人は各自考えてみてください！

さて，実際に実行して以下のようにして散布図を描画してみましょう

import matplotlib.pyplot as plt
%matplotlib inline
x, y ,actual_r = generate_values()
plt.scatter(x, y, alpha=0.3)
plt.title('r={:0.2f}'.format(actual_r))

import matplotlib.pyplot as plt

%matplotlib inline

x, y ,actual_r = generate_values()

plt.scatter(x, y, alpha=0.3)

plt.title('r={:0.2f}'.format(actual_r))

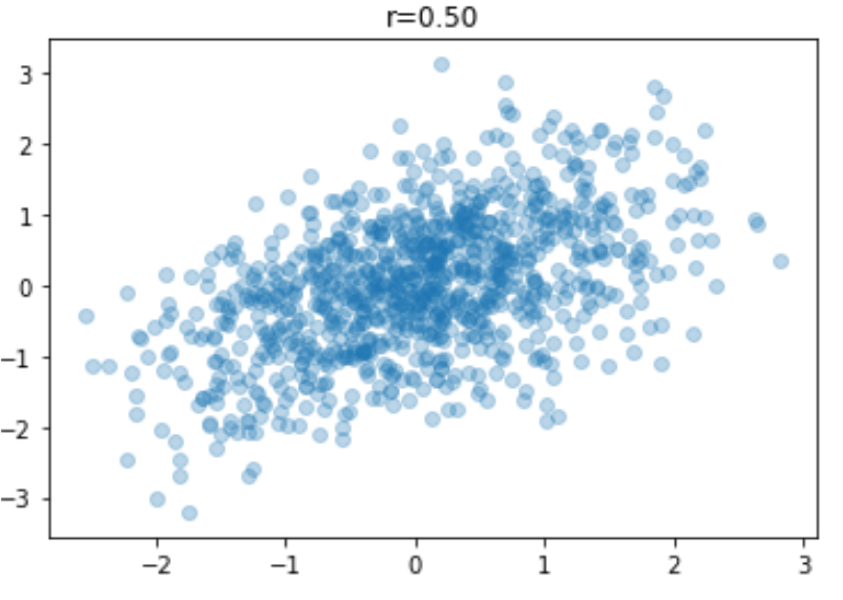
値はランダムで生成されるので，必ずしも実際の相関係数が0.5になるわけではないので注意してください．

では，この関数を使って相関係数が-1から1までのケースを一気に表示してみましょう！これをやるには以下のようにコードを書けばOKです．

# -1から1の相関係数の散布図を0.1単位で表示したい(計21個)

# 7x3の図を表示する(計21個なので)
rows = 5
cols = 5
figsize = (10, 10)
fig, ax = plt.subplots(rows, cols, figsize=figsize)
for idx, r in enumerate(np.arange(-1, 1.1, 0.1)):
    # 各plotのどこに配置するかを計算
    row_i = idx//cols 
    col_i = idx%cols
    #相関係数に対してランダムな値を計算
    x, y, actual_r = generate_values(r=r)
    #生成したランダム値から実際の相関係数を表示
    title = 'r={:.2f}'.format(actual_r)
    ax[row_i, col_i].set_title(title)
    ax[row_i, col_i].scatter(x, y, alpha=0.3, s=1)
# タイトルや軸が重なってしまうのを防ぐ
fig.tight_layout()

# -1から1の相関係数の散布図を0.1単位で表示したい(計21個)

# 7x3の図を表示する(計21個なので)

rows = 5

cols = 5

figsize = (10, 10)

fig, ax = plt.subplots(rows, cols, figsize=figsize)

for idx, r in enumerate(np.arange(-1, 1.1, 0.1)):

# 各plotのどこに配置するかを計算

row_i = idx//cols

col_i = idx%cols

#相関係数に対してランダムな値を計算

x, y, actual_r = generate_values(r=r)

#生成したランダム値から実際の相関係数を表示

title = 'r={:.2f}'.format(actual_r)

ax[row_i, col_i].set_title(title)

ax[row_i, col_i].scatter(x, y, alpha=0.3, s=1)

# タイトルや軸が重なってしまうのを防ぐ

fig.tight_layout()

先ほどの任意の相関係数に対してランダムな値を生成するコードは重要ではありませんが，このように複数のplotをfor文で描画するのは非常に重要です．書けるようにしておきましょう！データサイエンスの現場では本当によく使うコードなので押さえておきたいところです．

この辺りは大人気の動画講座の応用編でめちゃくちゃ詳しく解説しています．こちらの動画講座を受講いただければこういうコードを簡単に書けるようになると思うので，是非受講ください．

【公開初日で受講生1000人超え！】データサイエンスのためのPython動画講座を公開しました【全23時間…!!】

さて，上の図をみると，なんとなくですが相関係数が0.7くらいから，散布図が明らかに群になって傾いている感じがわかると思います．逆に相関係数が0の時と0.2の時を見比べてみてください．あまり違いは無いようにも思えますよね？なので0.2以下はほぼ相関なしといっても良さそうです．

相関係数だけをみるのは危険？散布図も合わせて見ておこう

先ほど，相関係数に合わせた散布図をみたんですが，気になる変数間の相関を見る場合はなるべく散布図を見るようにしましょう！相関係数は，少しの外れ値や異常値によってその値が大きく変わりがちです．例えば前回までの記事のweightとheightの例をみてみましょう．

１つだけ外れ値を追加して相関係数を計算してみます

import numpy as np
weight = np.array([42, 46, 53, 56, 58, 61, 62, 63, 65, 67, 73])
height = np.array([138, 150, 152, 163, 164, 167, 165, 182, 180, 180, 183])
#外れ値追加前
r = np.corrcoef(weight, height)[0][1]
print('r={:.2f} (before adding outlier)'.format(r))
#外れ値追加
weight = np.append(weight, 70)
height = np.append(height, 0)
r = np.corrcoef(weight, height)[0][1]
print('r={:.2f} (after adding outlier)'.format(r))
plt.scatter(weight, height)
plt.xlabel('weight')
plt.ylabel('height')

import numpy as np

weight = np.array([42, 46, 53, 56, 58, 61, 62, 63, 65, 67, 73])

height = np.array([138, 150, 152, 163, 164, 167, 165, 182, 180, 180, 183])

#外れ値追加前

r = np.corrcoef(weight, height)[0][1]

print('r={:.2f} (before adding outlier)'.format(r))

#外れ値追加

weight = np.append(weight, 70)

height = np.append(height, 0)

r = np.corrcoef(weight, height)[0][1]

print('r={:.2f} (after adding outlier)'.format(r))

plt.scatter(weight, height)

plt.xlabel('weight')

plt.ylabel('height')

r=0.95 (before adding outlier)
r=-0.09 (after adding outlier)

1 2	r=0.95 (before adding outlier) r=-0.09 (after adding outlier)

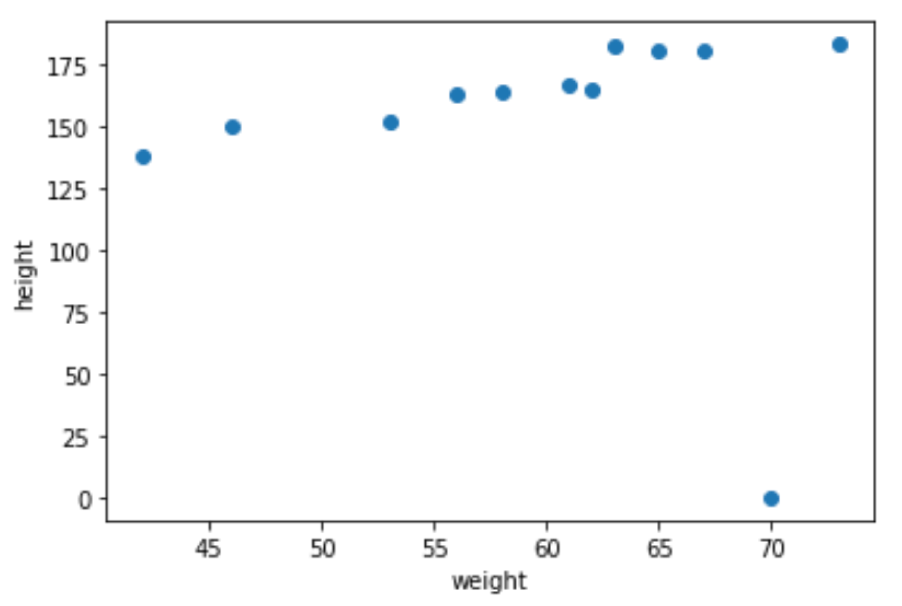
外れ値が１つあるだけで，かなり強い正の相関(r=0.95)が，無相関(r=-0.09)になってしまいました．

このように，少数の外れ値のせいで相関係数が間違った値になることが多いので注意です．なるべく散布図をみて，外れ値などがないかを確認するといいですね◎

外れ値の定義をどうするか
外れ値や異常値の特定には，ドメイン知識(そのデータの分野や背景知識)が必要になってきます．
例えば今回のケースでは「体重が0なんておかしい」というのがドメイン知識があれば分かるわけですね．よってこの値は，機器の異常だったりデータ収集時の人為的エラーだったり，データ処理によるなにかのエラーだったりというのが予想できるわけです．

相関関係と因果関係は区別して考えよう

よくある誤解が，相関関係を因果関係と勘違いしてしまうこと．

例えば今回のweight(体重)とheight(身長)のデータには強い相関関係がありました．これは一体なにを意味しているのでしょうか？

それは「身長が高い人ほど，体重が大きい傾向にある」という集団に対しての特性であることに注意しましょう．(このデータがある特定のデータの体重と身長の推移ではないと仮定します．)

つまり，「身長が高くなると，体重も大きくなる」ということを言っているわけではないんです．

さらにいうと，「身長が高いから，体重が大きい」というわけでもないんですね．これは，体重と身長を逆にして言うとわかると思います．

「体重が大きい人ほど身長が高い傾向にある」とは言えますが，「体重が大きくなると，身長も大きくなる」はずもなく，「体重が大きくなると，身長も高くなる」わけないですよね？

もし，一個目の「身長が高くなると，体重も大きくなる」ことを示したいのであれば，なにか身長を高くする操作をし，それに応じた体重の推移を個々のデータに対して観察する必要があります．

二個目の「身長が高いから，体重が大きい」というのは因果関係ですが，これはデータから証拠づけることは極めて難しいです．たとえある個人の身長と体重の時系列データを観察していったとしても，体重の増加を身長の増加だと原因づけることはできないことはイメージできると思います．ある時期に暴食して体重を増やしているだけかもしれませんよね．

もし，因果関係を決定づけるための実験をしたいのであれば，他の変数も考慮していく必要がありますし，実際に因果関係を明らかにするのは難しく，推論していくことになります．(このあたりはまた詳しく記事を書きたいと思います．)

とにかくここで重要なのは「相関関係は集合に対しての傾向を述べているだけでに留まり，個々のデータでの因果関係を述べるものではない」ということです．これはよくある誤解なので覚えておきましょう！

まとめ

今回は相関係数のポイントを３つ挙げました．どれもデータサイエンスにおいて非常に重要になってくるので，押さえておきましょう！

相関係数は0.7を超えると強い相関で，0.2以下はほぼ相関なし
相関係数だけをみるのは危険なので，できるだけ散布図も合わせて確認する
相関関係はあくまでも集団における傾向であって因果関係を示すものではない

今後も統計学の理論を学習するにあたって”相関係数”は非常に重要な役割を担ってくるので是非押さえておきましょう．

また，統計学を学習する際には是非Pythonで実装しながら学習しましょう！自分でコードを書くことで身につきますし，実際の現場でもすぐに役に立ちます．Pythonが不安な人は本ブログの講座や動画講座で学習してください．また，初学者の人は変な癖が着く前にプロによるコードレビューを受けておくことを強くお勧めします，

コミュニティDataScienceHubでは，毎週Pythonの課題を出していて，自由にコードレビューを受けたり，他の人が指摘されている点や他の人のコードを見ることができます．こんな機会はなかなかないと思うので，是非ご活用ください！