等分散性の検定(F検定)をわかりやすく解説【統計学入門34】

（追記）全16時間の統計学動画講座を公開しました！☆4.8の超高評価をいただいている講座です．こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください．

統計学入門第34回です．今回の記事でPythonで学ぶデータサイエンス入門:統計編は一旦終わりにしようと思います．(次回の記事で総集編を書いて締めます)

といっても，まだまだデータサイエンティストなら知っておきたい統計の知識はたくさんあります．分散分析やノンパラメトリック検定，他の分散の検定(ルビーン検定やバートレット検定)や因子分析，検定力分析など，統計学は本当に奥が深いです．これ以外にもベイズ統計ももう一つ大きな統計の分野です．

なので，今回の連載は超入門編ということで本記事で一旦締め，後日（需要があれば．．．）中級編(後編?)として続きを書いていきます！

二つの母集団の分散が等しいのかを検定する

今まで比率差の検定，連関の検定，平均値差の検定，を見てきましたが，「分散が等しいのかどうか」というのを検定することもできます．このような検定を等分散性の検定と呼んだりします．

一見「分散の検定なんて，何に使うの？分散なんてみんな興味ないでしょ！」と思うかもしれませんが，小標本の平均値差の検定(t検定)では二つの母集団の分散が等しいことを前提に理論を構築していました(第32回参照)．

なので，分散の検定はt検定の前段階で使われることが多いです．(他にも等分散を前提にしている分析がありますが，まだ扱っていないので気にしなくてOK)

等分散性の検定には色々なものがありますが，今回は2つの母集団の分散の検定に特化した，F検定というものを紹介します．

F検定は，今までのZ検定やt検定と同様，検定統計量がF分布という確率分布に従います．

F分布は色々な表し方があるが故に多くの方が混乱し，難しく思われがちですが，そんなに難しいものではないので今回の記事で理解しちゃいましょう！！

F分布は二つの分散の比率

F検定では分散の比率を見ます．分散の比率を見て，その比率がどれくらいの確率で起こりうるのかで帰無仮説を採択or棄却していきます．

今回も具体例はPythonのコードの時に紹介するとして，まずは記号で理論の説明をしていきます．

第32回同様，ある二つの母集団(平均がそれぞれ\(\mu_1, \mu_2\), 分散が\({\sigma_1}^2, {\sigma_2}^2\)とします)からそれぞれ標本(\(n_1\)個と\(n_2\)個)を取ってきて，それぞれの標本の平均を\(\bar{x}_1, \bar{x}_2\), 不偏分散を\({s’_1}^2\),\({s’_2}^2\)とします．

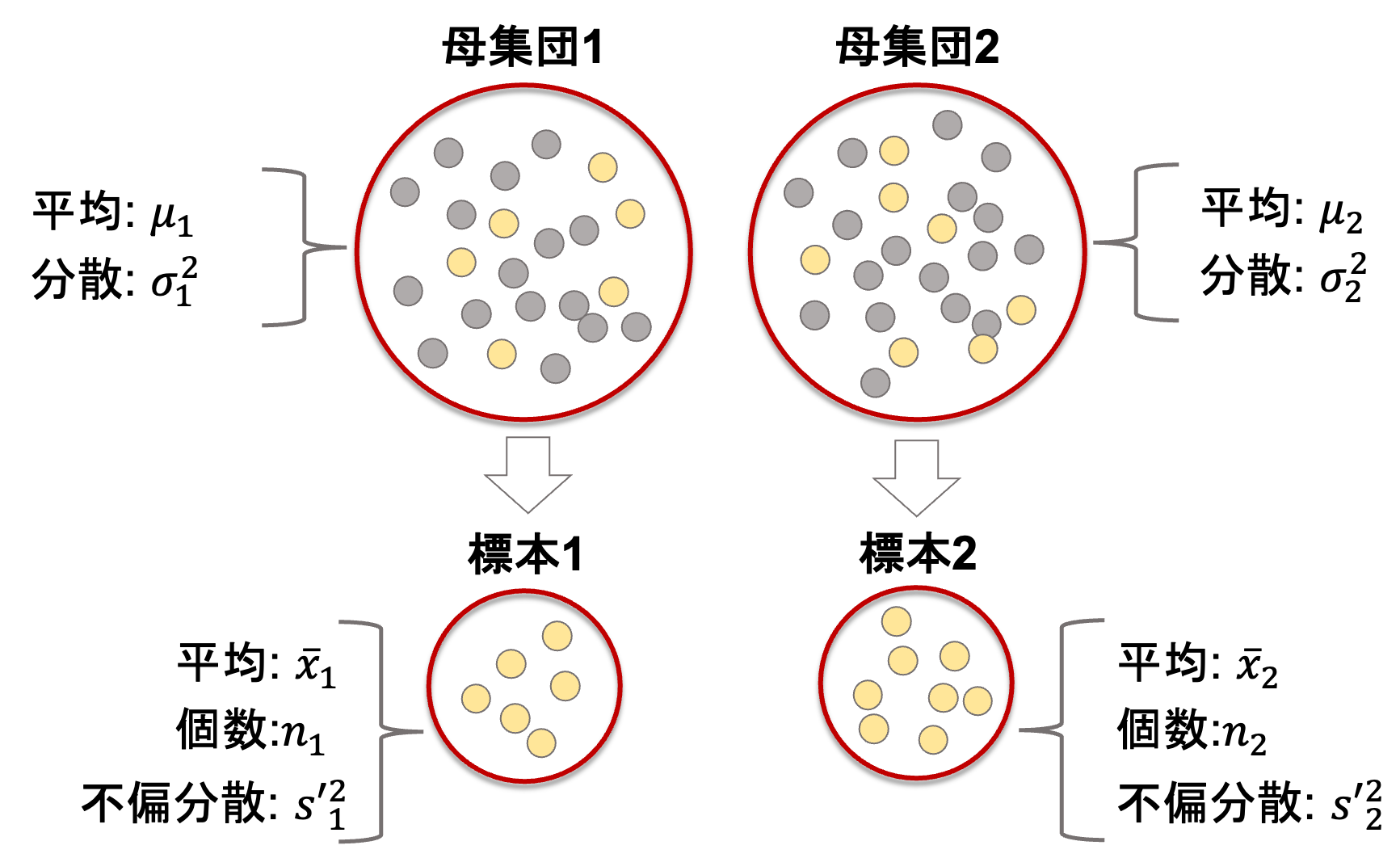
これも今まで通りですね．

ここで，二つの標本の不偏分散の比は，やはり一つの確率変数になります．(通常，大きい方を分子に置きます．)

$$F=\frac{{s’_1}^2}{{s’_2}^2}$$

この「不偏分散の比」が従う確率分布をF分布と呼びます．Fは，イギリスの統計学者のロナルド・フィッシャーからきてます．

めちゃくちゃ簡単じゃん！

そうなんです．めちゃくちゃ簡単なんですが，F分布は\(\chi^2\)を用いた表し方をよくし，そちらの方が多用されます．そして，F分布にも自由度があり，上の式では，自由度\(n_1-1\)および\(n_2-1\)のF分布に従うことになります．

それではまず，\(\chi^2\)を使った式について説明していきます．\(\chi^2\)については第31回で「\((観測度数-期待度数)^2/期待度数\)の総和値」として解説していますが，母集団が平均\(\mu\)，分散\(\sigma^2\)の正規分布から値をn個(\(x_1, x_2,…,x_n\))取り出した時，\(\chi^2\)を以下のように表すことができます．

$$\chi^2=\sum^{n}_{i=1}\frac{(x_i-\bar{x})^2}{\sigma^2}$$

「\((観測度数-期待度数)^2/期待度数\)の総和値」という式と見比べても，そこまで違いはないかと思いますが，こちらの式も重要なので見慣れておきましょう．

ここで不偏分散\(s’^2=\frac{1}{n-1}\sum^{n}_{i=1}(x_i-\bar{x})^2\)(第5回参照)を使って書き換えると，

$$\chi^2=\sum^{n}_{i=1}\frac{(x_i-\bar{x})^2}{\sigma^2}=\frac{(n-1)s’^2}{\sigma^2}$$

と表すことができます．これは自由度\(n-1\)の\(\chi^2\)分布となります．

さて，先ほどの\(F=\frac{{s’_1}^2}{{s’_2}^2}\)ですが，\(\chi^2=\frac{(n-1)s’^2}{\sigma^2}\)から

$$F=\frac{\frac{1}{n_1-1}\chi^2_1\sigma^2_1}{\frac{1}{n_2-1}\chi^2_2\sigma^2_2}$$

と表すことができ，それぞれの母分散は等しい(\(\sigma^2_1=\sigma^2_2\))という帰無仮説を考慮すると，

$$F=\frac{\frac{1}{n_1-1}\chi^2_1}{\frac{1}{n_2-1}\chi^2_2}$$

となります．

この式からも，F分布の自由度が\(n_1-1\)および\(n_2-1\)になるのがわかると思います．自由度が二つあることに違和感があるかもしれませんが，F値は二つの標本の組み合わせで成り立つ値であり，それぞれの標本がそれぞれの自由度を持っていて，その組み合わせによって分布の形が変わると思えば納得できるのではないでしょうか？

F分布を見てみよう！

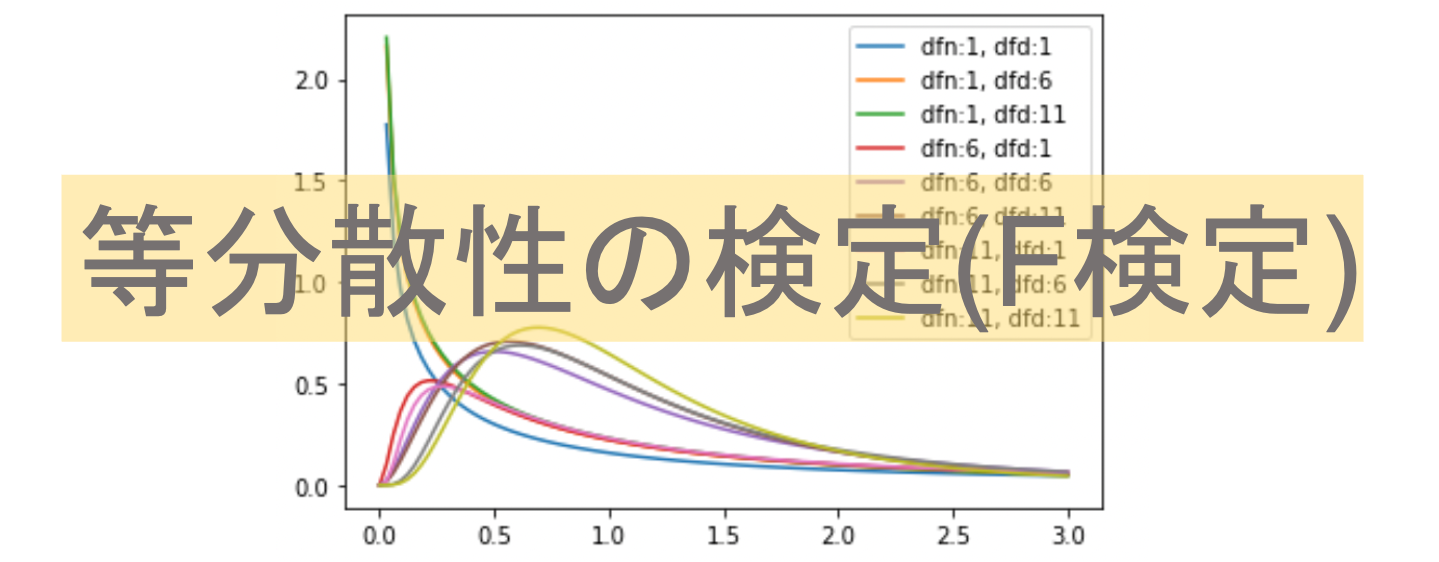
さて，いつも通りF分布を見てみましょう！今回もお馴染みのstatsモジュールの stats.f を使います．

それぞれの自由度に色々な値を入れて描画し，F分布がどのような分布になるか見てみます．

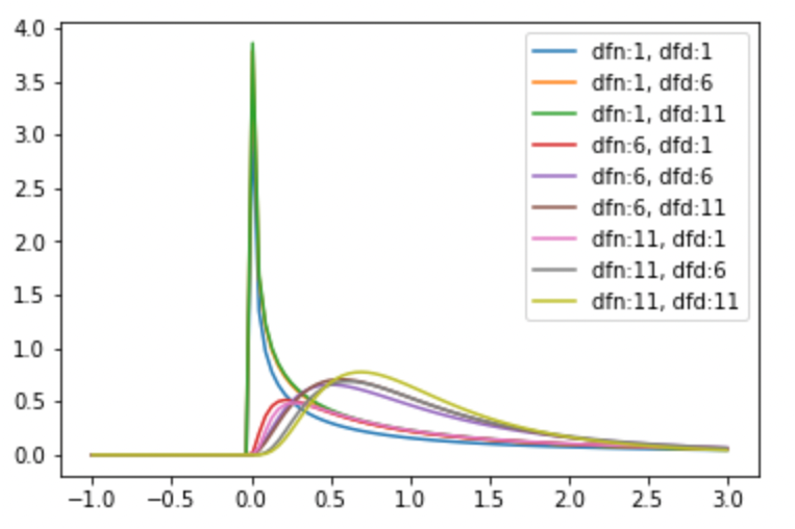
自由度が二つあるので少し複雑に見えますが，それぞれの自由度で様々な形をとることがわかると思います．分散は正の値しか取ることがないので，F分布もx軸の値は全て正の値になっています．

F検定では，F値を計算し，指定した自由度のF分布においてそのF値が棄却域に入るかをみていけばいいわけですね．

PythonでF検定をやってみる

それでは，前回の記事同様にタイタニックデータを使って，生存者および非生存者の年齢の分散が等しいと言えるのかどうかをF値とF分布を使って検定してみましょう．

statsモジュールには簡単にF検定をしてくれる関数が用意されていないので，先ほど紹介した stats.f を使ってやっていきます．

（なお，このやり方は他の検定も同じように使えるので是非押さえておきましょう！）

1.前回の記事を参考にタイタニックデータを用意し，csvファイルからDataFrameにし，空白のデータをdropしておきましょう

2. 生存者，非生存者にグループを分けます．今回は年齢にのみ興味があるので，Age項目だけとりだしてSeriesにします

（この辺りのDataFrameの処理はデータサイエンスのためのPython動画講座で詳しく解説しています．超高評価動画なので，この辺りの処理が不安な方は是非受講ください．）

3. それぞれの標本の大きさ( n1 および n2 )と不偏分散( var1 ,  var2 )，自由度( dfn , dfd )を求めます (今回は var2 の方が大きくなるので， dfn には age2 の自由度を入れます．)

4. F値を計算します　(今回は var2 の方が大きいので var2 を分子にします．)

分子に大きい方の分散を置くので，必ずF値は1以上になります

5. 計算したF値がF分布でどれくらいの確率で起こりうるのかを計算する．

これには .cdf() を使えばOKです． .cdf() は前回の記事でも使いましたね．Cumulative Density Functionの略で，日本語では累積分布関数と言います．

この0.699という数字は，左からF値(1.117)まで累積した面積（＝F分布からF値を取り出した時，1.117以下の値になる確率）です

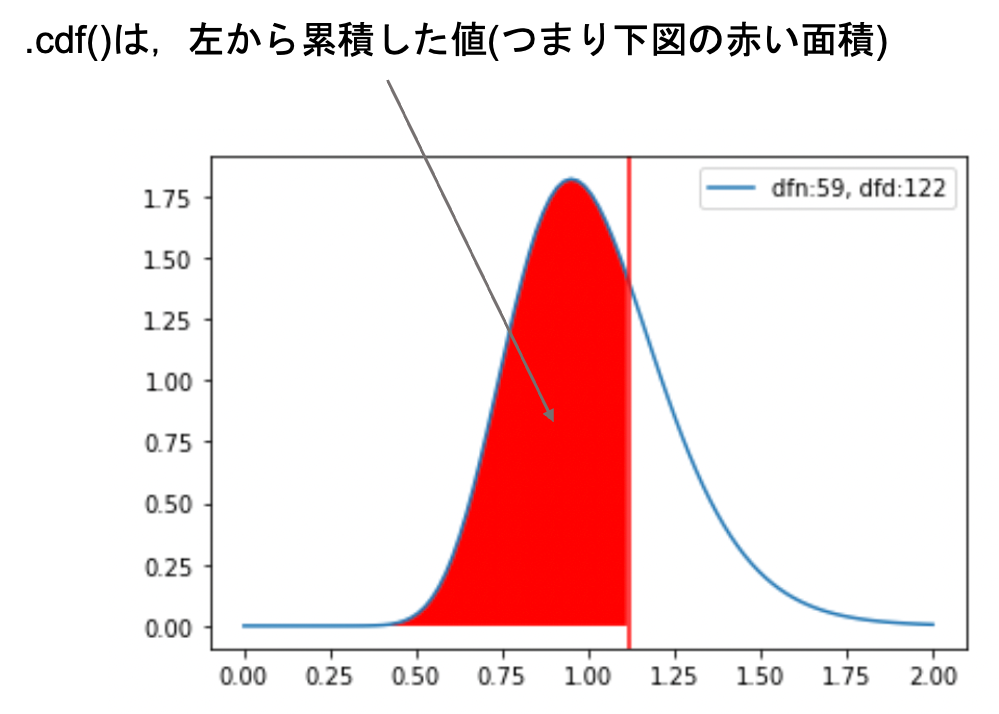
今回は分子に大きい方の分散を置いているので，F値は必ず1以上になります．なので今回求めたいp値はF値よりも右側の面積になります．(例えばF値が2などの大きい値であれば，右側の面積が<.05になり帰無仮説を棄却できることからもイメージできるかと思います．)

なので，今回求めたいp値は

となり，例えば有意水準を5%とするとp>.05なので「分散が等しい」という帰無仮説は棄却できず，「分散が異なるとは言えない」という結果になります．

※「分散が同じである」と結論付けることはできないことに注意しましょう

F検定は母集団が正規分布であることを前提にしている

F検定は，母集団が正規分布である標本同士についてのみ有効です．これは，先述の\(\chi^2=\sum^{n}_{i=1}\frac{(x_i-\bar{x})^2}{\sigma^2}\)の式が母集団が正規分布のときという条件付きであったことからもわかります．

つまり，F検定の前に「正規分布の標本なのか？」ということを評価する必要があります．これは分布をみたり検定したりして評価していきます．

検定の種類に「正規性の検定」というものがあり，色々種類があります．この辺りも今後の統計学講座後編に扱っていきたいと思います．

今回はひとまず正規性の検定の一つ，シャピロ=ウィルク検定というものをやってみます． stats.shapiro() 関数で簡単に行うことができますが，詳細な理論は今後詳しく述べていきます．