決定係数R2を超わかりやすく解説【統計学入門16】

こんにちは，米国データサイエンティストのかめ(@usdatascientist)です．

Pythonで学ぶデータサイエンス入門：統計編第16回です．

（追記）全16時間の統計学動画講座を公開しました！☆4.8の超高評価をいただいている講座です．こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください．

前回までの記事で線形回帰についてみてきました．

今回の記事では，回帰分析において非常に重要となる決定係数という指標について解説していきます．

決定係数は統計学のみならず機械学習においても非常に重要な指標ですが，きちんと理解している方はかなり少ない気がします．

論文等にもよく載せる指標ですが，統計ツールを使ってパパッと出してなんとなく載せているという人もいるのではないでしょうか？

今回はそんな「決定係数」を超超わかりやすく解説していきます！

え？「決定係数ってなに？？」

大丈夫，そんな人でも全部理解できるように解説します！

決定係数とは？？

決定係数は，一言で言うと「説明変数がどれだけ目的変数の値を説明(決定)しているかの指標」です．

全く意味がわからないので帰って寝ます．

待って，帰らないでええ！！

難しく聞こえるかもしれませんが，全然難しくないし，この指標は非常に重要なのでちゃんと理解していきましょう！

(前回までで使っていた体重と身長の例でいうと)例えば体重50kgの人と体重60kgの人がいたとします．

この2人の体重の差って，身長の差がどれだけ関係しているのか，言い換えれば身長がどれだけ説明しているのかを考えましょう．

もし２人の身長が同じなら身長は関係ないですが，もし体重50kgの人の身長が165cmで，体重60kgの人の身長が170cmだとしたら，2人の体重の差の一部は身長の差によるものだと言えそうです．

違う例でもう一度説明します．

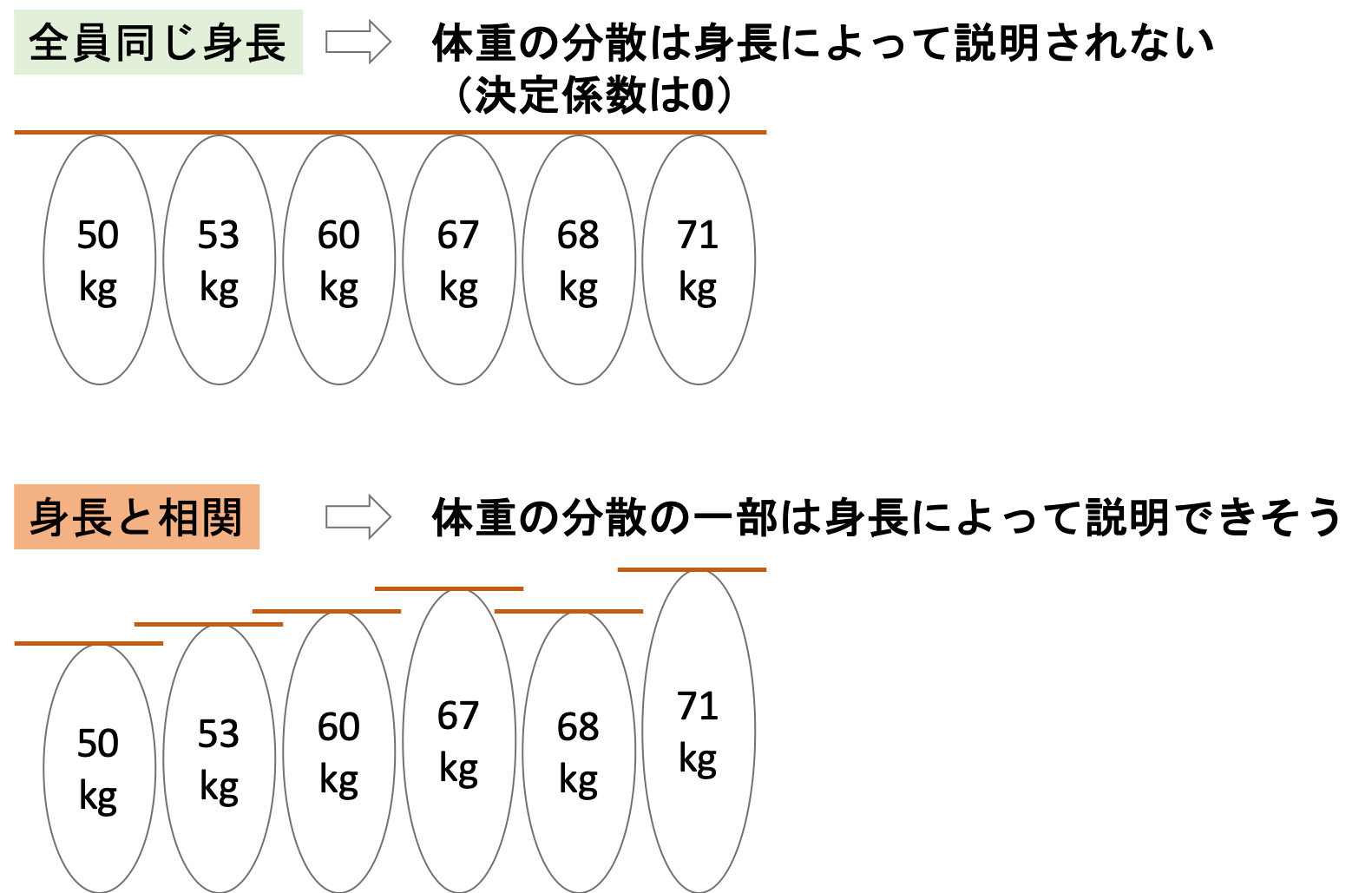
例えば体重50kg, 53kg, 60kg, 67kg, 68kg, 71kgの人たちがいたとしましょう．

この体重のばらつきを身長がどれだけ説明しているのか？というのが決定係数の意味するところです．

んーちょっとまだよくわからない．．．

例えば全員が同じ身長だったら・・・・？

身長が体重のばらつきを一切説明していないことになります(後述しますが，この場合決定係数は０になります．)

一方体重が大きい人の方が身長が高い場合，体重のばらつきの一部は身長によるものだと言えそうですよね？

つまり，「$y$の分散は，$x$によってどれだけ説明(決定)されるか」というのことです．

決定係数の定義

今まで通り，身長を$x$体重を$y$とします．n人の身長と体重のデータがあったとして，身長のことは気にせず，単純に体重の分散を計算すると以下のようになりますよね?（分散についてはこちらの記事をご確認ください．）

$$s_y^2=\frac{1}{n}\sum^{n}_{i=1}{(y_i-\bar{y})^2}$$

つまり単純に体重の平均$\bar{y}$からの偏差の平方和をとっているだけです．

しかし，この$s_y^2$の一部は，きっと身長$x$の差異によるものですよね？その割合が決定係数と呼ばれる指標です．

では，この$s_y^2$のうち身長$x$によってどれくらいの割合で説明されるかを知るにはどうすればいいでしょうか？

これを知るには，「身長$x$によって”説明されない”体重$y$の分散」を考えて，それを$s_y^2$から引けばよさそうです．

では，「身長$x$によって”説明されない”体重$x$の分散」を求めることを考えてみましょう．

これを求めるには，「同じ身長の人たちでどれだけ体重がばらつくか」を考えれば良さそうですよね？

例えば全てのデータのうち，身長160cmのデータだけを集めて，その中の体重の分散を考えます．

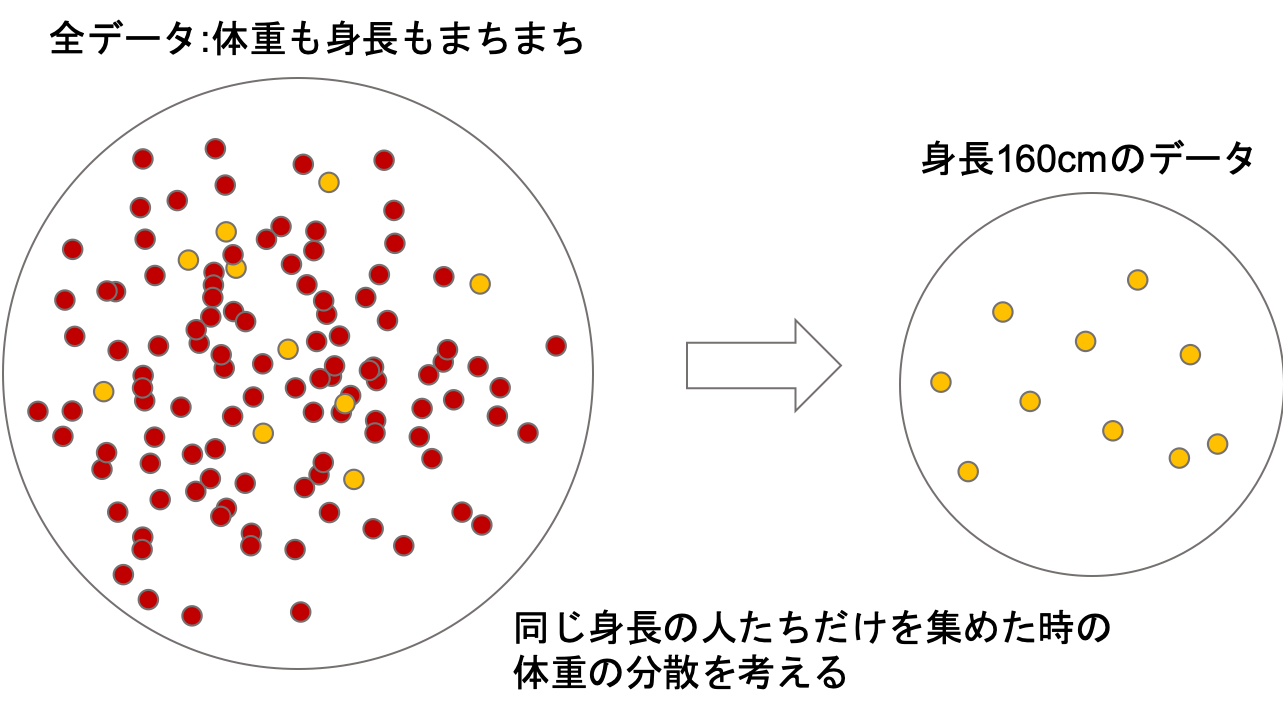
身長160cmの人たちだけのグループの体重の分散は，もとのデータの体重の分散$s_y^2$よりかは小さくなりますよね？(様々な身長の人たちの体重より，同じ身長の人たちの体重の方がばらつきは小さい)

そしてこのグループの体重の分散は，身長にはよらないものと考えることができます(だってみんな同じ身長だからね！)

これを応用して，身長が同じ人たちの間での分散を考えるために以下の式で定義される$s_{y\cdot x}$を考えます．

$$s_{y\cdot x}=\frac{1}{n}\sum^{n}_{i=1}{(y_i-\bar{y}_{x_i})^2}$$

$\bar{y}_{x_i}$は，身長$x_i$における平均体重です．つまり，$i$番目の人の体重の偏差を，全ての人の体重の平均$\bar{y}$からではなく，その人と同じ身長の人の平均的な体重$\bar{y}_{x_i}$からの偏差を求めているわけです．

ちょっとややこしく思えるかもしれませんが，この式を覚える必要はないです．重要なのは，$s_{y\cdot x}$は体重の分散のうち身長によって説明されない部分だということです．

第13回の記事で，回帰直線は条件付き平均だという話をしました．これは，$x=x_i$において計算される$y=a+bx_i$の値は，$x=x_i$における$y$の平均値ということです．

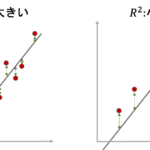
つまり，身長$x_i$における平均体重$\bar{y}_{x_i}$は，回帰直線で計算される$y=a+bx_i$のことなんですね．これがわかれば，以下の図が理解できるのではないでしょうか？

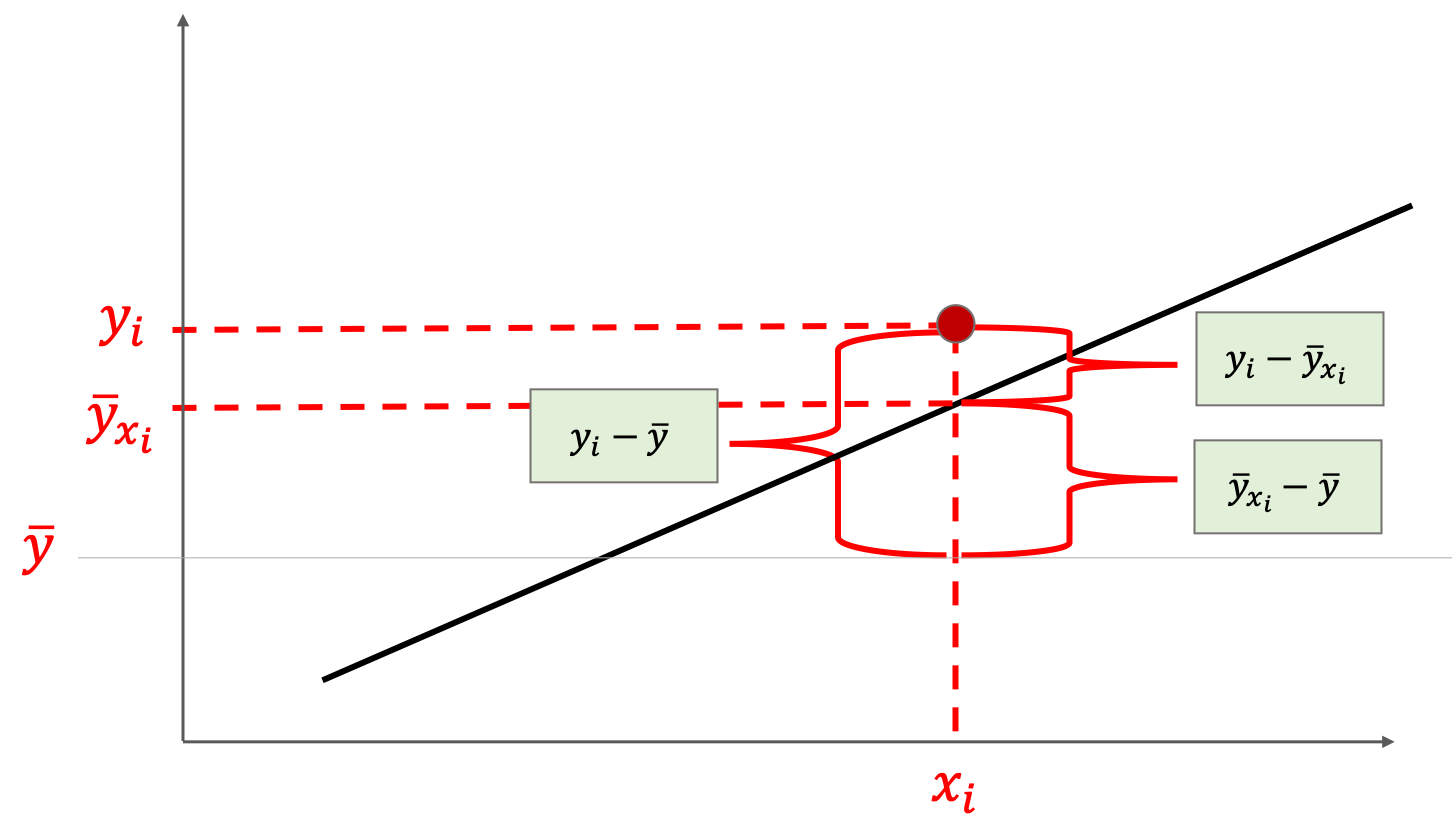
こちらの図は，$x$から$y$を予測する回帰直線です．不要な箇所は全てはしょってます．

丸ポチの赤い点$(x_i, y_i)$が実際に観察されたデータの一つです．この$y_i$の偏差$y_i-\bar{y}$は，$\bar{y}_{x_i}-\bar{y}$と$y_i-\bar{y}_{x_i}$に分けることができますよね？

前者の$\bar{y}_{x_i}-\bar{y}$は回帰直線で計算された$y$の値の$\bar{y}$からの偏差です．つまりこれは「$x=x_i$における平均的な$y$の値の偏差」だといえます．

身長と体重の例を使って噛み砕いて言うと，「身長が$x_i$の人たちの平均的な体重$\bar{y}_{x_i}$の偏差」です．この部分は「偏差$y_i-\bar{y}$のうち身長によって説明できる部分」と言えます．

もう一度上の図の赤い点$x_i, y_i$を見てください．$y_i$は$\bar{y}_{x_i}$よりもう少し上に位置しています．

これは「この人の身長における平均的な体重よりも少しばかり体重が重い」ことを意味しています．この平均的な体重との差($y_i-\bar{y}_{x_i})$は「身長によって説明できない部分」と言えます．

イメージでいうと，ある人(身長160cm, 体重60kg)が「自分の体重が重いのは，そりゃ身長があるからですよ」と言うのに対して，「いやいや，あなたの身長の平均的な体重は50kgなので，残りの10kgは身長では説明できない部分ですよ．」と言えるわけですね．

以上を踏まえると↓が理解できるのではないでしょうか？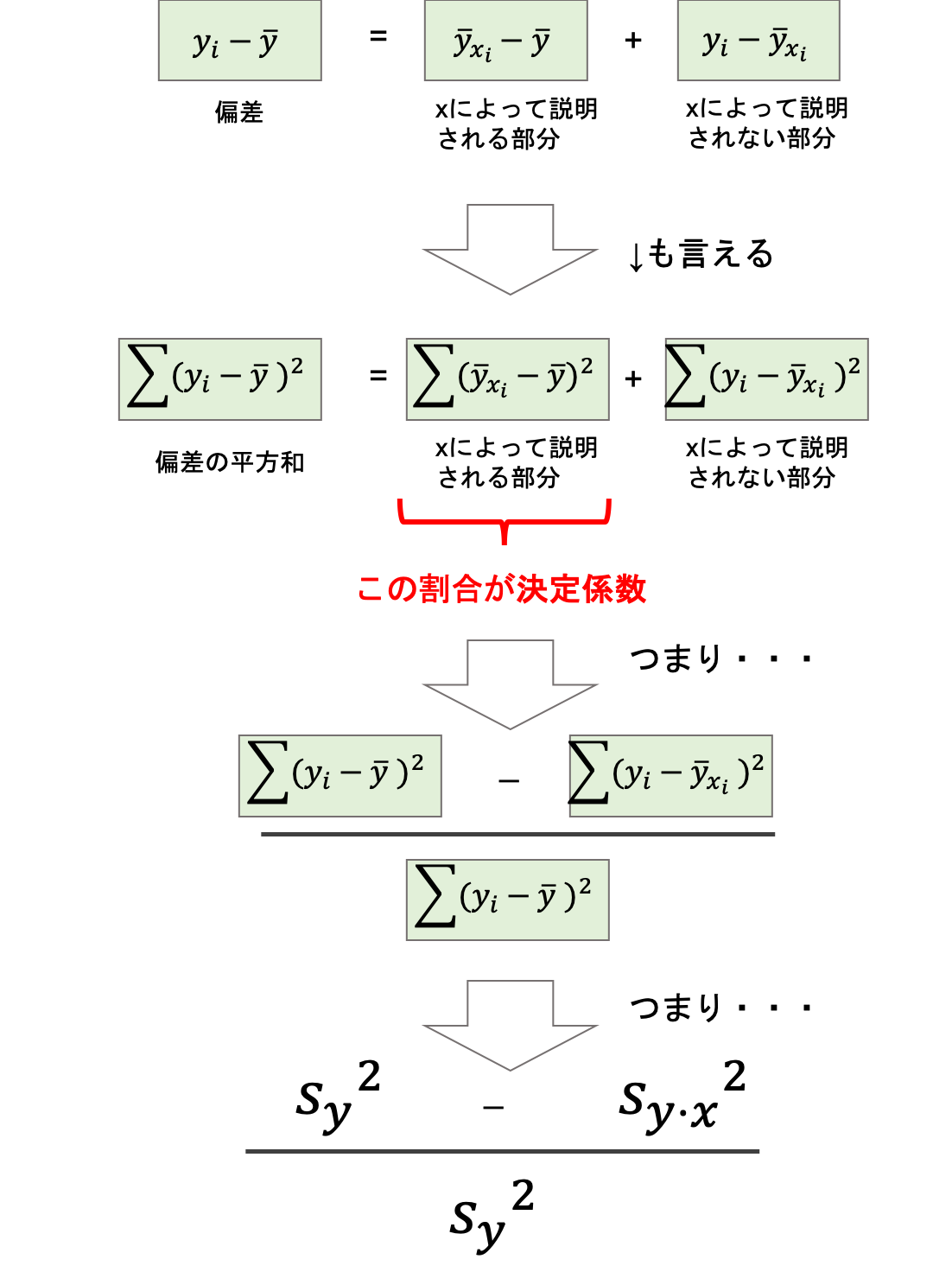

証明は(重要ではないので)飛ばしますが，とにかく上の図での偏差の分解が分散の分解に繋がるところを意識しておきましょう．

以上から，「$y$の分散のうち$x$によって説明される割合い」は以下のように定義でき,これを決定係数(coefficient of determination)といい通常$R^2$(R squared)で表します．

$$R^2=\frac{s_y^2-s_{y\cdot x}^2}{s_y^2}=1-\frac{s_{y\cdot x}^2}{s_y^2}$$

回帰直線が最小二乗法によって求められた場合，この$R$は相関係数$r$と一致します．これは非常に重要なことなので覚えておきましょう！

$R^2$=0ということは，上記の式から$s_{y\cdot x}^2=s_y^2$ということです．つまりこれは，xがまったくyを説明(決定)していないと言うことになります．

一方$R^2$=1というのは，$s_{y\cdot x}^2$が0ということで，つまり先ほどの回帰直線の図で全ての$i$で$y_i-\bar{y}_{x_i}$が0ということになり全てのデータが回帰直線上に位置している(完全な正の相関がある)ということです．この場合$x$が完全に$y$を決定していると言えます．