データサイエンス入門の機械学習編第17回です.(講座全体の説明と目次はこちら)
追記)機械学習超入門動画講座を公開しました!動画で効率よく学習をしたい人はこちら(現在割引クーポン配布中です)
今回の記事では,前回の記事で紹介したロジスティック回帰を多クラス分類に適用する方法を紹介します.
ロジスティック回帰の理論は,基本的に2クラスの分類です.多クラス(=目的変数が3つ以上の値を取りうるケース)分類の場合は少し工夫が必要です.
実際の業務では2クラスよりも多クラス分類の方が圧倒的に多いと思うので,今回の記事でしっかり学んでいきましょう!
目次
ロジスティック回帰を多クラス分類に応用するための二つの方法
通常のロジスティック回帰は2クラス分類(2値分類: binary classification)にしか対応していないため,多クラス分類に応用するには工夫が必要です.
やり方は二つあります.
- One vs Rest (OvR)
- 多項ロジスティック回帰(Multinomial logistic regression)
One vs Restは,一つのクラスとそれ以外の全クラスの2値分類器をクラスの数だけ作って最終的に多クラス分類にするやり方です.
多項ロジスティック回帰は,多クラス用に損失関数を書き換えたものでOvRとは異なり直接多クラスに対しての予測結果を計算するやり方です.

...だと思うので,一つ一つ丁寧に解説していくので是非読んでってください!笑
この二つをごっちゃにしている人が多い印象で,なんとなーくロジスティック回帰を多クラスに使ってる人が多いと思います.
が,実は二つやり方があって,それぞれモデルの精度も異なってくるのでちゃんと区別できるようにしましょう!
One vs Rest (OvR)
One vs Restは,ロジスティック回帰のみならず他の2値分類のアルゴリズムを多クラス応用する際にも使える,機械学習の一般的な多クラス応用のやり方です.One vs Allとも言ったりします.
以下を例にしてみましょう.色(赤,青,黄)を分類するモデルを構築することを考えます.これは3クラス分類になるので,多クラス分類ですね.
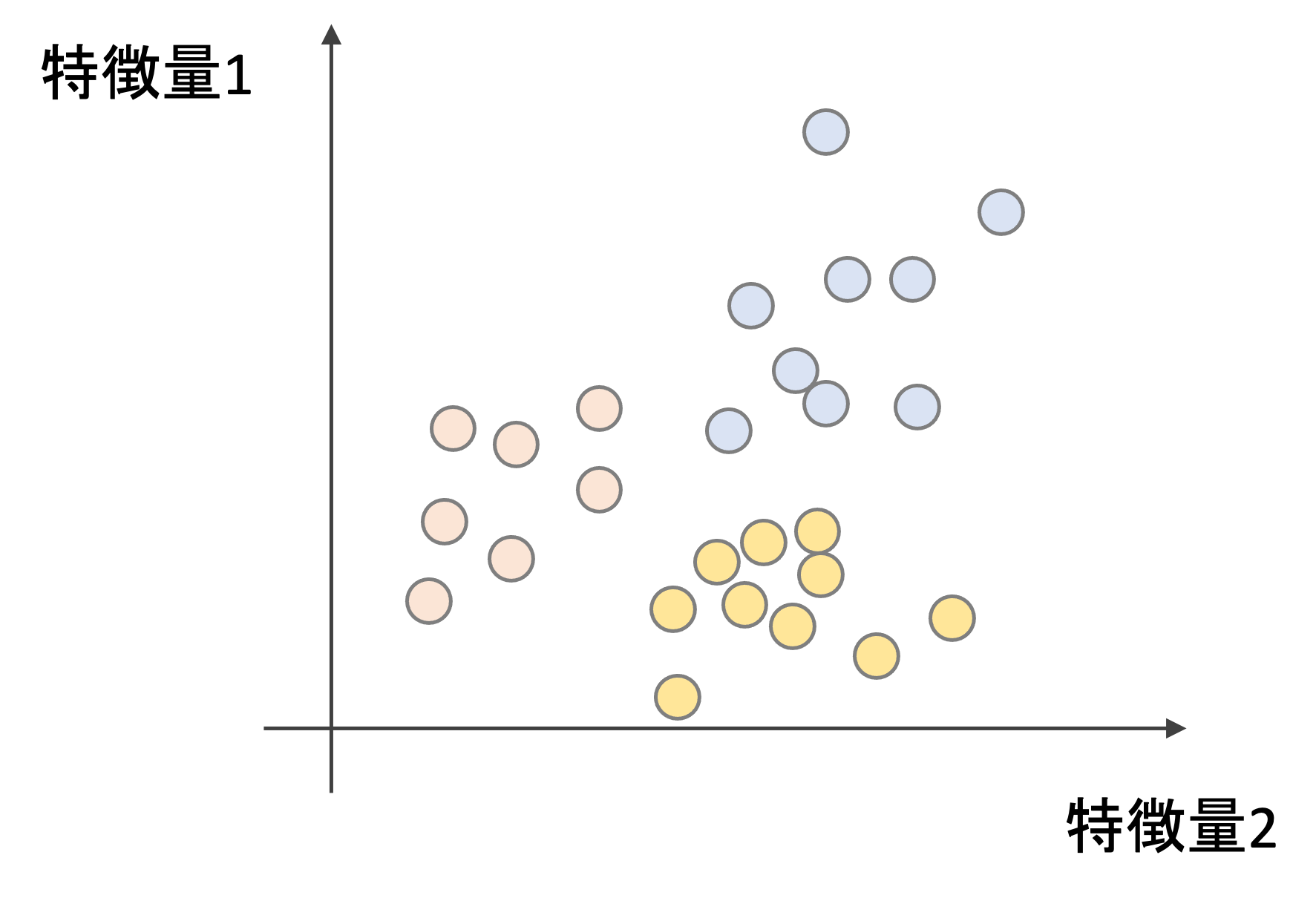
何かの2つの特徴量があって,それによって色を分類できると思ってください.適当です.例なんで!笑
One vs Restでは,以下の三つの分類器を作ります.
- 赤 vs その他(青,黄)を分類する分類器
- 青 vs その他(赤, 黄)を分類する分類器
- 黄 vs その他(赤,青)を分類する分類器
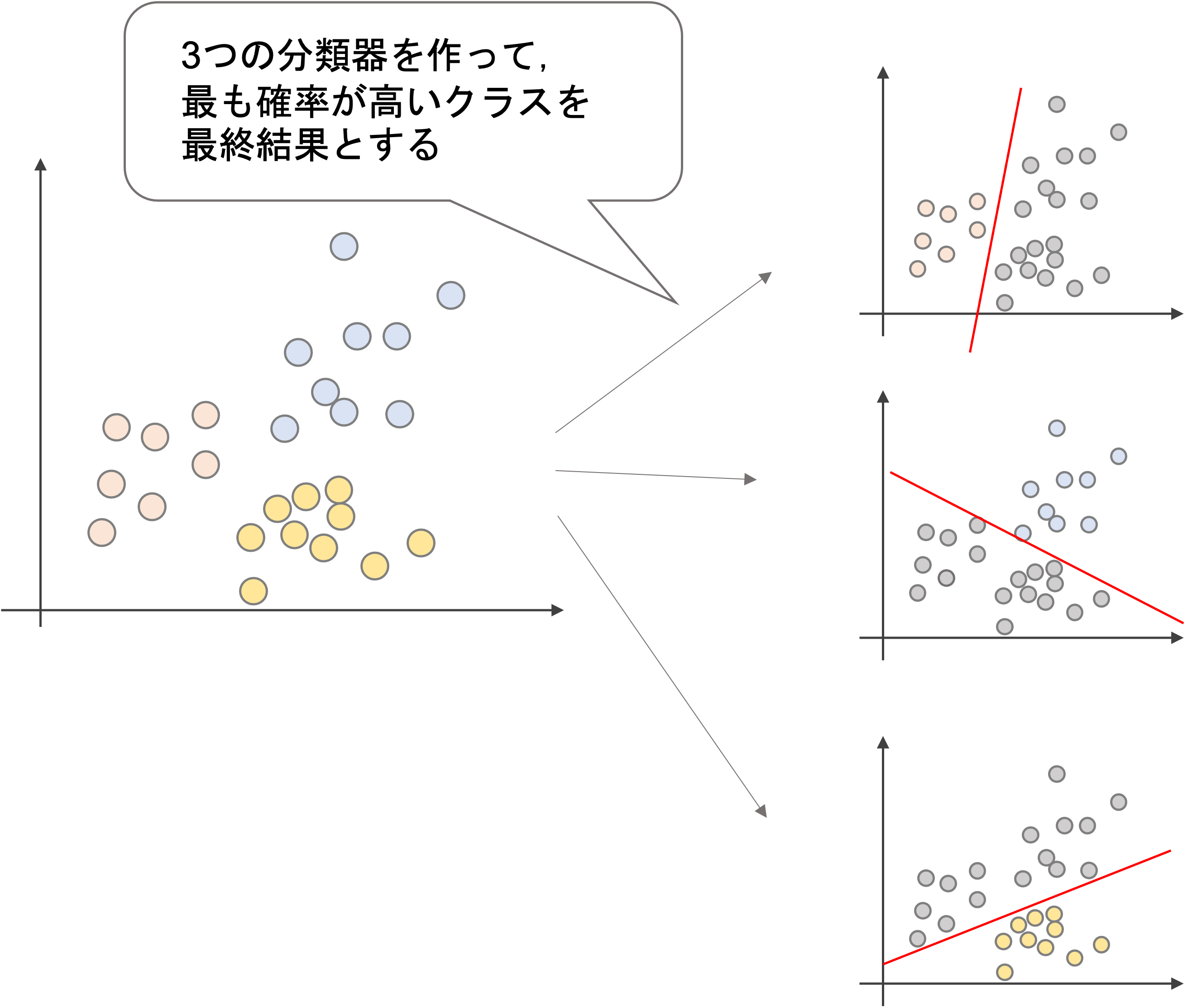
まさにOne vs Rest (一つのクラスとそれ以外のクラス)のモデルを作っていくわけですね!この三つの分類器の結果のうち最も高い確率のクラスを予測結果とします.
めちゃくちゃシンプルですよね?
この方法は現在でもよく使われる手法であり,2値分類のアルゴリズムを多クラス分類に応用する方法として最も一般的なやり方だと思います.が,データ数が多かったり,学習に高いリソースを使用するアルゴリズムでは,クラスの数分分類器を作る必要がでるので,そういった場合多くのコンピュータのリソースを消費することを覚えておきましょう
多項ロジスティック回帰(Multinomial logistic regression)
多項ロジスティック回帰(Multinomial logistic regression)は,本来2値分類用であるロジスティック回帰の損失関数を多クラスにも適用できるように変更したバージョンです.特に区別せず「ロジスティック回帰」と呼ぶことが多い印象ですが,厳密には多クラス分類の場合はこのような名前がついています.

$$L(\theta)=\frac{1}{m}\sum^{m}_{i=1}Cost(p(x_i), y_i)=-\frac{1}{m}\sum^{m}_{i=1}y_ilog(p(x_i))+(1-y_i)log(1-p(x_i))$$
式を見てわかるように,前回の記事で紹介したlog loss (交差エントロピー)の損失関数の式は2クラスの時にしか使えないので,多クラス用に損失関数を少し工夫する必要があります.
目的変数のエンコーディング
2値分類の場合は,単純に目的変数を0/1と変換してシグモイド関数を適用していました.
が,3つ以上のクラスの場合はどうしましょうか.0/1/2/…と数字を単純に連番で割り振ることはできません.これは前回の記事でも話したように,質的変数を量的変数のように扱うことはできないからですね.(例えば赤,青,黄の3クラス分類をするとして,それぞれ0, 1, 2と数値を割り当てたとしても,青(1)が黄(2)の半分の値というわけではないので,数値として扱うことはできません)
ここで出てくるのがone hot エンコーディングです.
例えば赤,青,黄の3クラス分類では,以下のようにエンコーディングします.
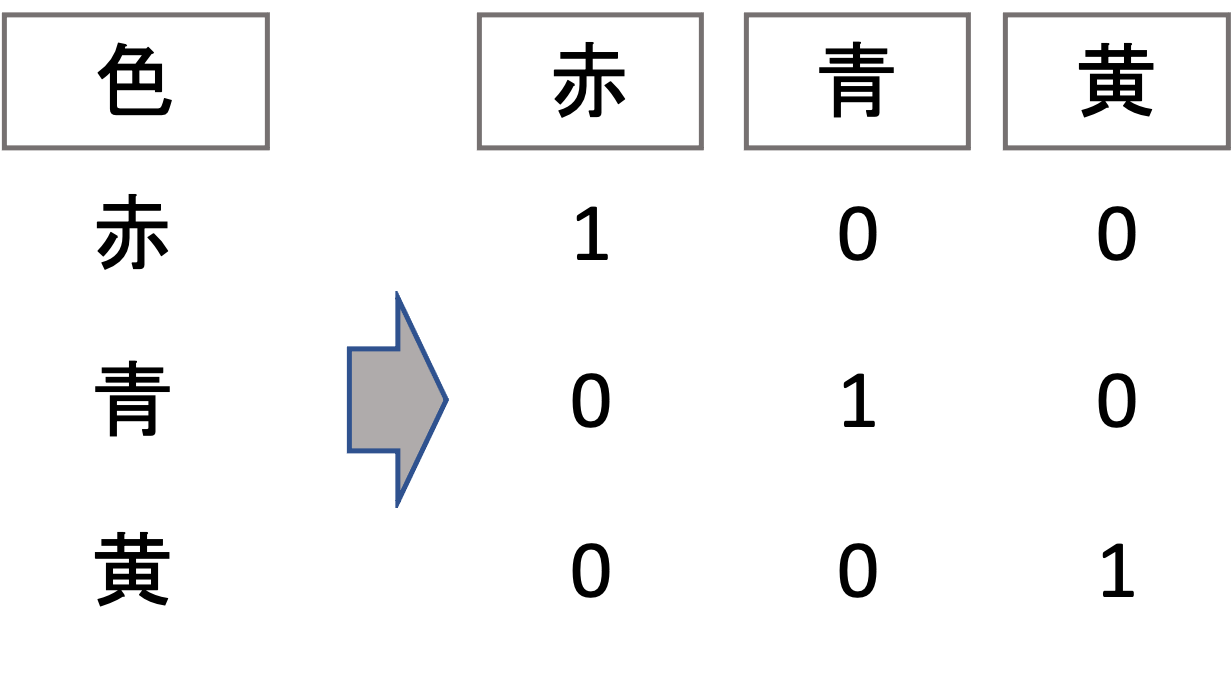
今回は説明変数ではなく目的変数のエンコーディングなので,ダミー変数トラップを意識する必要はありません.
数式で表す場合,以下のように定義できます.
\begin{equation}
t_{ik}=\left\{
\begin{aligned}
1 \qquad\text{if}\:y_i=k\\
0 \qquad\text{if}\:y_i\neq k\\
\end{aligned}
\right.
\end{equation}
ソフトマックス関数
2クラス分類ではシグモイド関数を使っていましたが,多クラス分類ではソフトマックス関数(softmax function)というのを使います.
ソフトマックス関数は,シグモイド関数の多クラスバージョンだと思ってください.
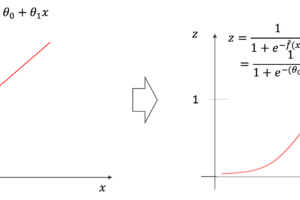
前回の記事で紹介したシグモイド関数は以下の式でした.
$$z=\frac{1}{1+e^{-x}}$$
この\(z\)の値を,2値分類の片方のクラスに属する確率として使っていたのでした.
実際には2つのクラスがあるので,片方は\(z\),もう片方は\(1-z\)ですね.
この式を\(x=x_1-x_2\)とし,\(x_1\)の\(x_2\)からの差分を入力と考えてみましょう.式を変形すると
$$z=\frac{1}{1+e^{-(x_1-x_2)}}=\frac{1}{1+\frac{e^{x_2}}{e^{x_1}}}=\frac{e^{x_1}}{e^{x_1}+e^{x_2}}$$
のようになります.これは\(x_1\)に対しての確率と見ることができ,逆に\(x_2\)に対しての確率は\(1-z\)なので
$$1-z=1-\frac{e^{x_1}}{e^{x_1}+e^{x_2}}=\frac{e^{x_1}+e^{x_2}}{e^{x_1}+e^{x_2}}-\frac{e^{x_1}}{e^{x_1}+e^{x_2}}=\frac{e^{x_2}}{e^{x_1}+e^{x_2}}$$
となるのがわかります.つまり,前回の記事で紹介したシグモイドは,\(x_2=0\)とした形だと思ってください(式の意味は変わりません.)
これを,クラス数が増えていくと以下のように一般化できると思います.これがソフトマックス関数です.
$$p_k(x)=\frac{e^{x_k}}{e^{x_1}+e^{x_2}+\cdots+e^{x_K}}=\frac{e^{x_k}}{\sum_{k=1}^{K}e^{x_i}}$$
ただし\(K\)はクラス数です.この式を各クラス毎に計算し足し合わせたら1になるのがわかると思います.このことから,この値を各クラスの確率として扱うことができます.(そのため\(x\)に対してのクラス\(k\)の確率\(p_k(x)\)としています.)
実際の多項ロジスティック回帰では,\(x_k\)は線形回帰モデルの出力結果なので,\(\theta^k_0+\theta_1^kx\)の形をとります.(特徴量が複数ある場合も同様ですが,シンプルにするため今回は特徴量一つのケースで書いてます)
$$p_k(x)=\frac{e^{\theta^k_0+\theta_1^kx}}{\sum_{k=1}^{K}e^{\theta^k_0+\theta_1^kx}}$$
ソフトマックスの式をいきなり見ると「???」になってしまいますが,このようにシグモイド関数を一般化した形だと思えばピンとくるのではないでしょうか?
ソフトマックス関数は機械学習では頻出の関数です.深層学習でもよく出てくるので,是非この機会に覚えてしまいましょう!
ソフトマックス関数を使えば,どのような値でも,最終的に確率の形になることを意識しておいてください.
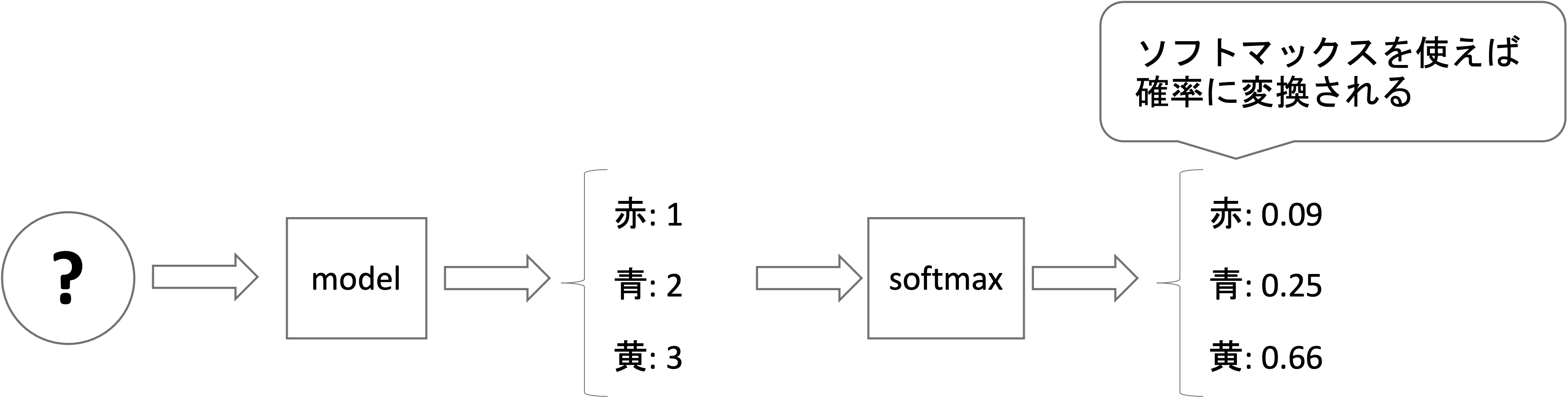
単純にそれぞれの割合を計算するのではなく,指数関数(\(e^x\))をとって確率にしています.この辺りはシグモイド関数も同じでしたね.
多項ロジスティック回帰の損失関数
さて,いよいよ多項ロジスティック回帰の損失関数をみていきましょう!
2値分類の時の損失関数は,正解クラスに対する確率の値のlogarithmの負の値を損失としていました.
\begin{equation}
Cost(p(x_i), y_i)=\left\{
\begin{aligned}
-log(p(x_i)) & \qquad\text{if}\:y_i=1\\
-log(1-p(x_i)) & \qquad\text{if}\:y_i=0\\
\end{aligned}
\right.
\end{equation}
例えば,本当は正解がラベル1のデータを0の確率0.3, 1の確率0.7としたら,シンプルに損失は\(-log(0.7)\)でしたね.
これを単純に複数のクラスに拡張してあげればOKです.
例えば,正解が”赤”のデータに対して赤,青,黄の確率をそれぞれ0.5 0.3, 0.2と出力した場合,損失は\(-log(0.5)\)になります.他のラベル(クラス)の確率は損失には入ってきません.非常にシンプルですね!

これを式で表すと以下のようになります.交差エントロピーの多クラスバージョンです.(前回の記事に合わせて今回は平均をとります.合計でもOKですよ.)
$$L(\theta)=-\frac{1}{m}\sum^{m}_{i=1}\sum^{K}_{k=1}t_{ik}logp_k(x_i)$$
ただし,\(i\)は\(i\)番目のデータで総数を\(m\), クラス数は\(K\)とし,\(p_k(x_i)\)は「\(i\)番目のデータ\(x_i\)の\(k\)番目のクラスである確率」を表しています.
また,\(\theta=\theta^1_0, \cdots, \theta^K_0, \theta^1_1, \cdots, \theta^K_1\)で,特徴量が複数ある場合も同様に\(\theta^1_2, \cdots, \theta^K_2\))のように追加されていくと思ってください.
\(t_{ik}\)は同じく\(i\)番目のデータにおいて,正解ラベルが\(k\)であれば1, それ以外では0になる値です.先程のone-hot エンコーディングをした正解ラベルです.
つまり,正解クラス以外のクラスに対する確率は\(t_{ik}=0\)により損失にはカウントされないということですね!
式は一見複雑そうに見えますが,やってることは普通のことですね.
さて,今度はこの損失関数が最小になるパラメータ\(\theta\)を計算すればいいんですが,これも解析的に求めることはできないので最適化問題として解いていきます.
損失関数の偏微分
先程の\(L(\theta)\)を\(\theta\)で偏微分していきます.実際の\(\theta\)は\(\theta=\theta^1_0, \cdots, \theta^K_0, \theta^1_1, \cdots, \theta^K_1\)と複数あることに注意してください!(式が見にくくなるのでこのようにしています)
この偏微分は,そこまで難しくはないのですがやはり長くなるので本講座では割愛します・・・
偏微分の結果は以下のようになります.
$$\frac{\partial L(\theta)}{\partial\theta^k_0}=\frac{1}{m}\sum^{m}_{i=1}(p_k(x_i)-t_{ik})$$
$$\frac{\partial L(\theta)}{\partial\theta^k_1}=\frac{1}{m}\sum^{m}_{i=1}(p_k(x_i)-t_{ik})x_i$$

そうなんです!\(x_i\)は\(x_i\)は\(i\)番目の特徴量\(\theta^k_1\)に対応する\(x\)です.もし特徴量が複数ある場合も同様です.
この形はどこかで見たことありますよね?2値分類のロジスティック回帰の損失関数の偏微分と比べてみましょう.
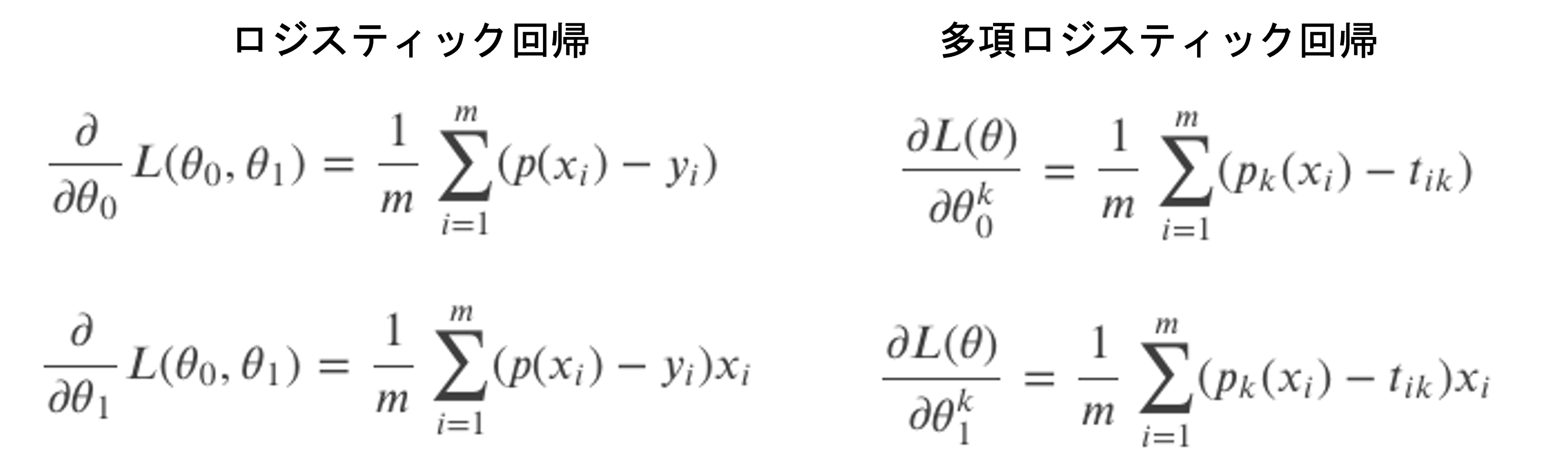
多クラス用に記述が変わっている箇所がありますが,結果は同じ形をしているのがわかります.
この式を使って,あとは他のアルゴリズム同様にパラメータ\(\theta\)を更新していくことになります.(式は前回の記事を参考にしてください)
ようは,全体的に2値分類用の式を全部多クラス用に応用したって感じです.あまり難しく考えなくてOK!!
今回の記事はこれで終わりにします.式の導入を飛ばしてもかなり長くなってしまいましたね(汗
次回の記事ではPythonでロジスティック回帰のモデルを学習するやり方を紹介します!
まとめ
今回はロジスティック回帰を多クラス分類に応用するやり方を紹介しました.
- やり方は大きく二つ.One vs Restと多項ロジスティック回帰
- One vs Rest (OvR): それぞれのクラス毎に,そのクラスvs他の全クラスを分類する分類器を作成し,それらの分類器で最も確率が高いクラスに分類する
- 多項ロジスティック回帰: 2値分類専用だったロジスティック回帰を多クラスに応用する
- 目的変数をone-hot エンコーディングする
- シグモイド関数の一般形であるソフトマックス関数を使用する
- 多クラス用の交差エントロピーを損失関数とする
- 損失関数を\(\theta\)で偏微分し,パラメータを最適化問題で最適解を解く
次回の記事ではPythonで実際のデータに対してロジスティック回帰を使ってクラス分類するやり方を紹介します.
式だけ眺めてもいまいちピンとこないかもしれませんが,実際にデータに対して分類器を作って予測結果などを見れば,なんとなく理解できてくると思います!
それでは!
追記)次回の記事書きました!