サポートベクターマシンを図でやさしく理解する(理論+実装)【機械学習入門34】

機械学習入門講座第34回です．(講座全体の説明と目次はこちら)

今回の記事からは，サポートベクターマシンという機械学習のアルゴリズムを紹介します．

サポートベクターマシンは，1990年代に人気を博した機械学習アルゴリズムですが，その精度の高さからも今でもよく使われるアルゴリズムです．

機械学習をかじった人は聞いたことくらいはあると思います．

理論が少し難しいアルゴリズムですが，重要なところだけをかいつまんでわかりやすく解説するので是非この機会に理解して使えるようにしましょう！

SVM(Support Vector Machine: サポートベクターマシン)とは？

サポートベクターマシン(Support Vector Machine)は，SVMと略していうことが多いので，本講座ではSVMと呼ぶようにします．

SVMは，分類と回帰どちらにも使える機械学習アルゴリズムです．登場当時は非常に精度が高かったので，深層学習の登場までは最強のアルゴリズムとして君臨(?)してました．今でもよく使われることがあるアルゴリズムです．

本記事では分類器を例に解説をしていきます．

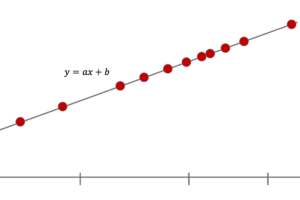
まず，以下のようなデータでの２クラスの分類問題について考えましょう．

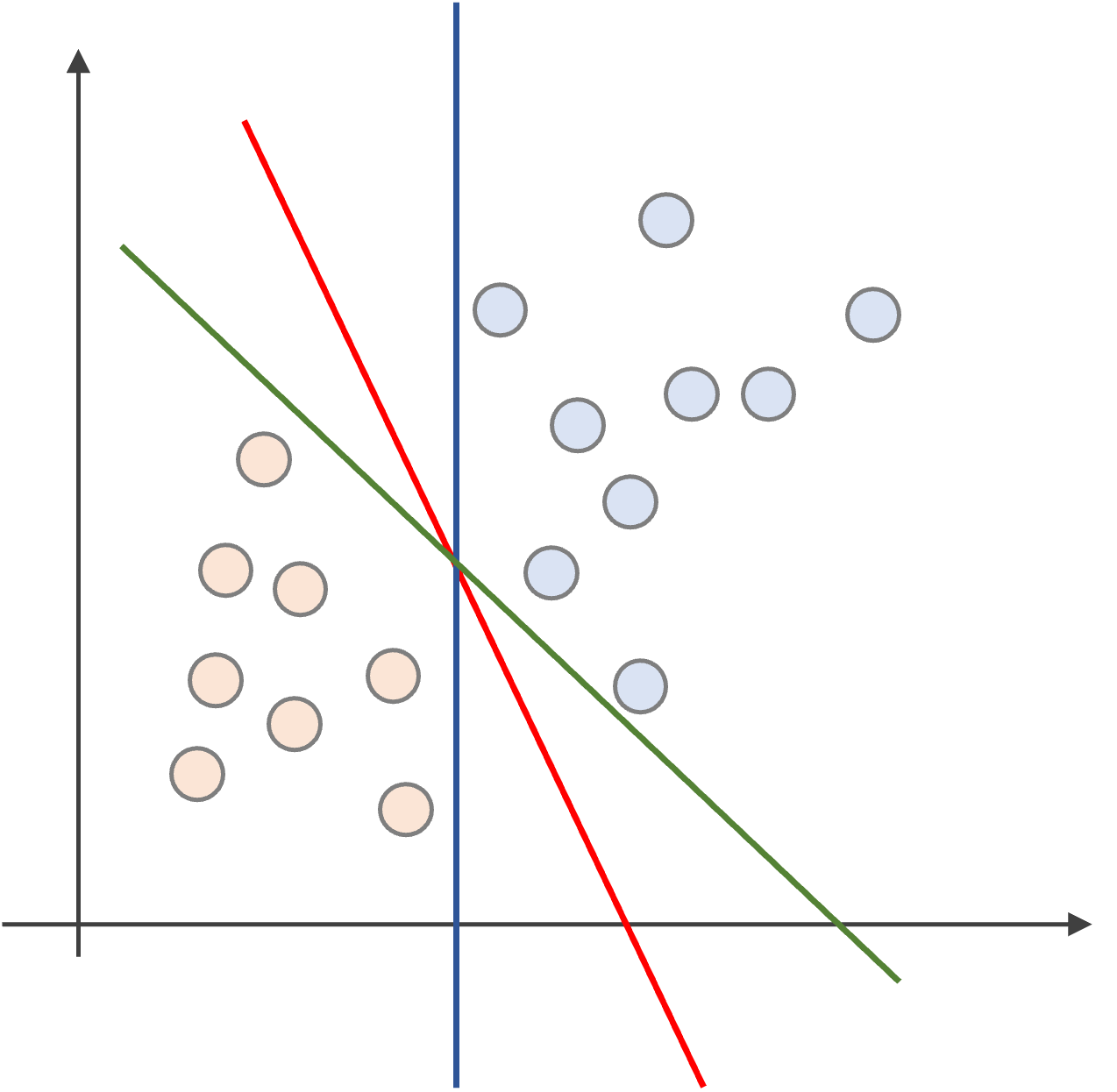
赤と青の二つのデータを分離する直線は無数に考えられますが，上記には３つの例(緑，赤，青)を記しています．

この三つの例では，明らかに赤が良さそうですよね？

緑や青の線だと，データにすれすれすぎて，新たなデータに対してうまく識別できなさそうですよね．

一方，赤の線は直近のデータからある程度余裕を持って線を引いています．

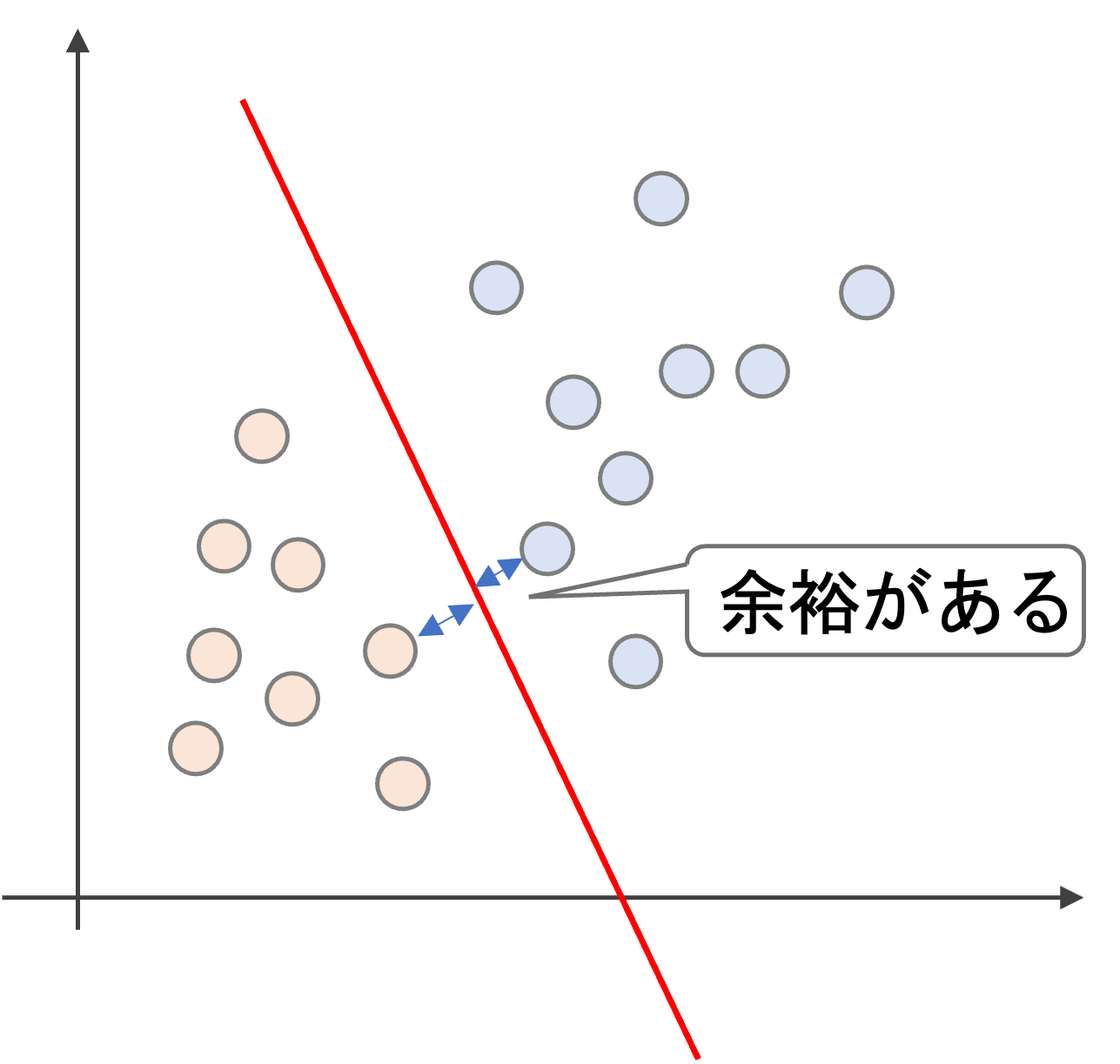
SVMは，

決定境界線は，余裕をもって引いた方が良さそう

というある意味当たり前な直感を利用します．

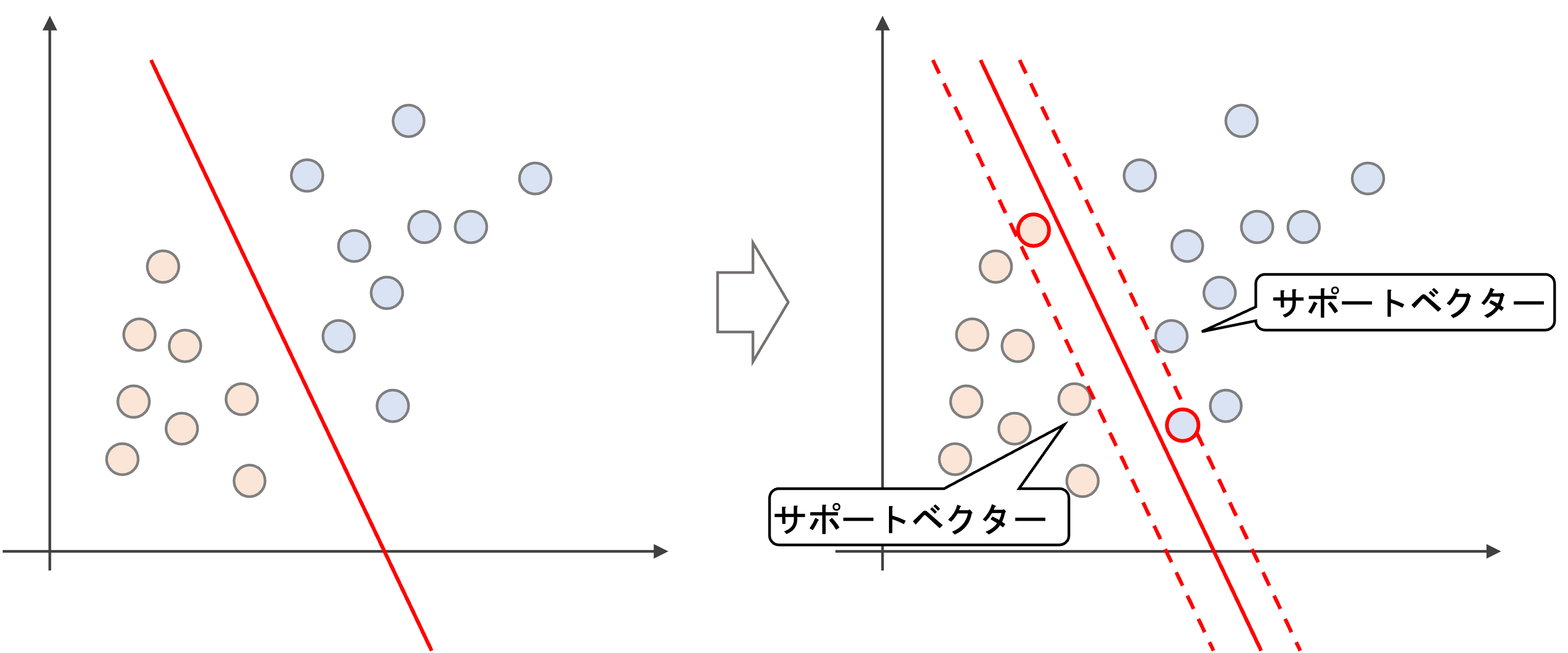
決定境界線から(“今回の例では”)直近のデータをサポートベクター(Support Vector)と呼び，サポートベクターから決定境界までの距離をマージン(margin)といいます．(常に”直近のデータ”がサポートベクターになるとは限りません．これについては後述します)

つまり，SVMではサポートベクターから最大限マージンを取るように決定境界をとります．

ハードマージンとソフトマージン

先ほどの例のように，はっきりとクラス分類するマージンをハードマージンといい，ある程度誤分類を許容するマージンをソフトマージンと言います．

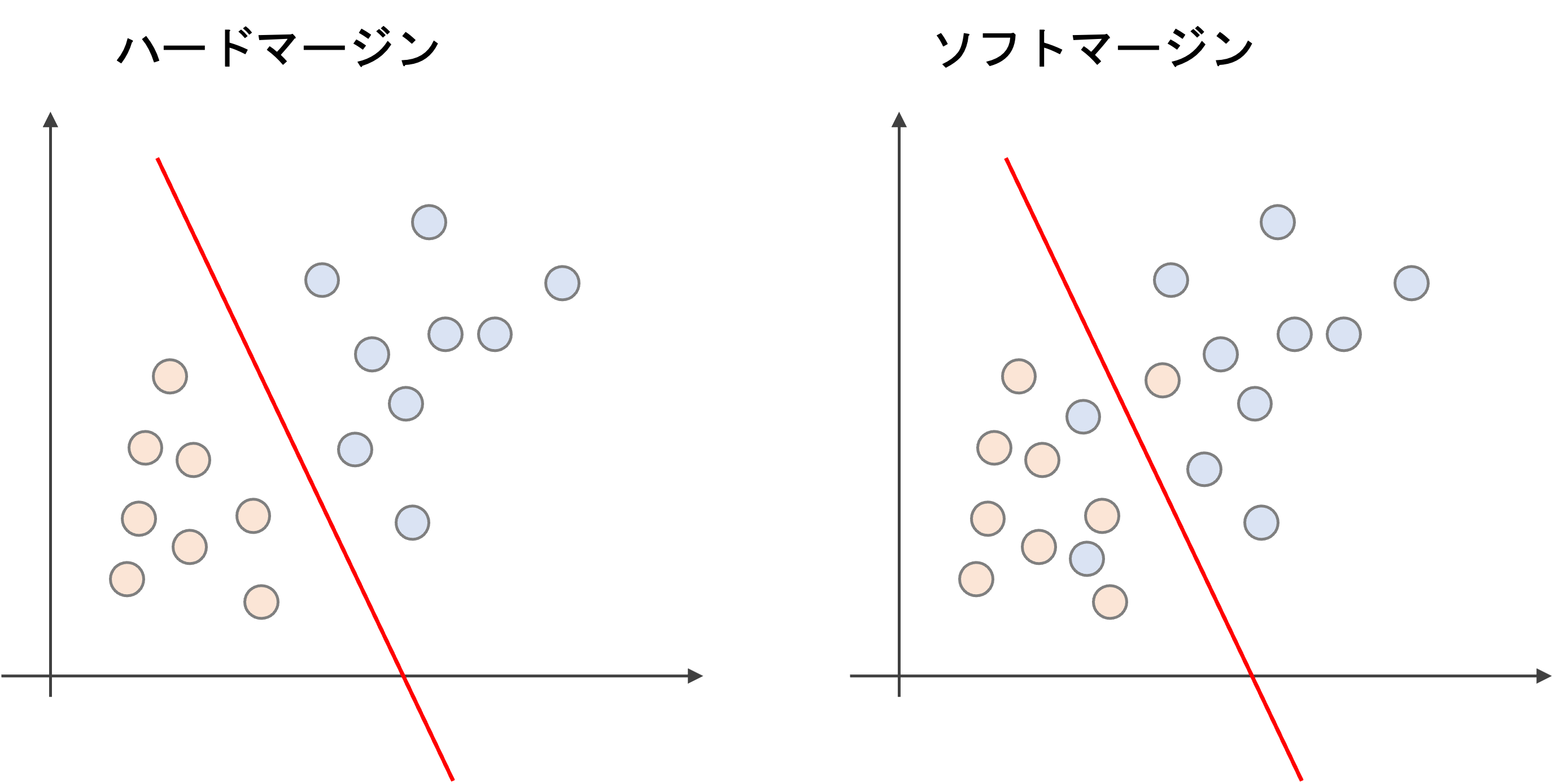
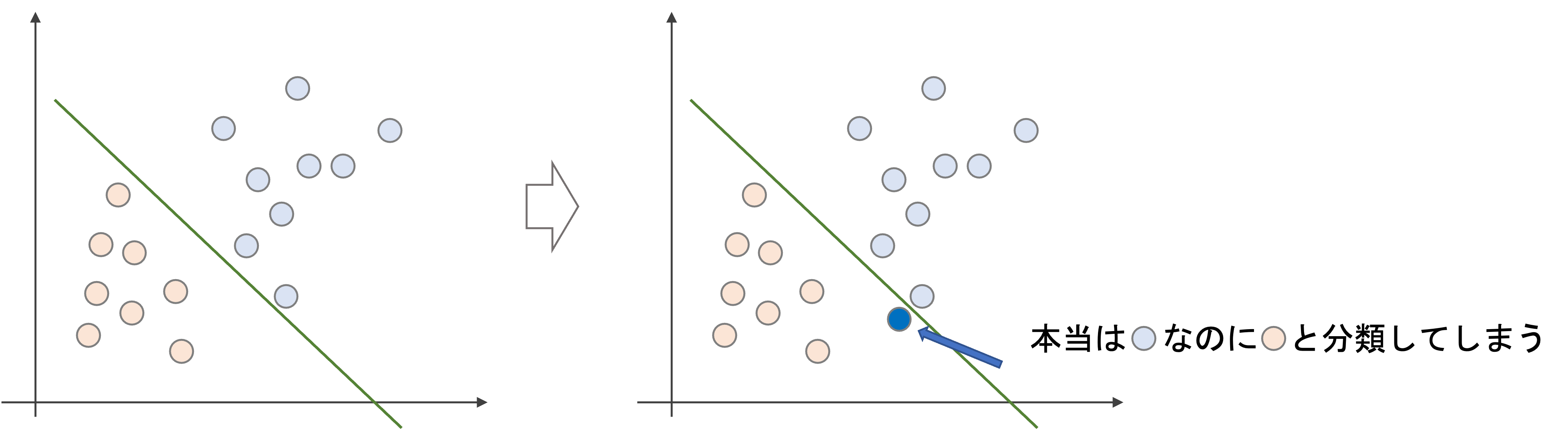
ハードマージンは，はっきりとクラス分類をしようとします．一見良さそうなんですが，実は問題があります．

ハードマージンでは，以下のように外れ値一つで境界が大きく変わってしまいます．これは過学習状態であり，bias-varianceでいうとhigh variance状態になってしまい，汎化性能が高いとは言えません

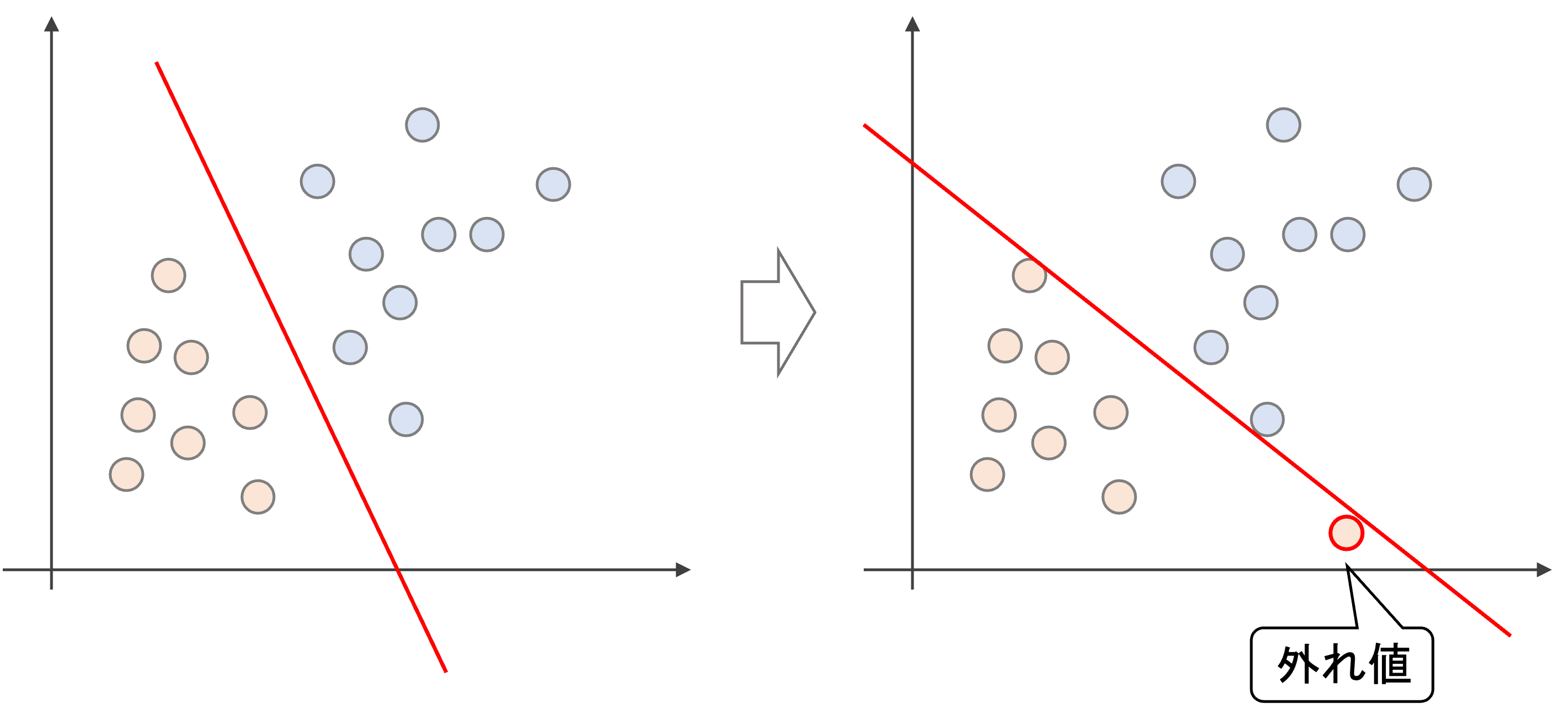
一方，ある程度誤分類を許容するソフトマージンでは，外れ値一つで大きく決定境界が変わることなく，ロバスト性が増します．

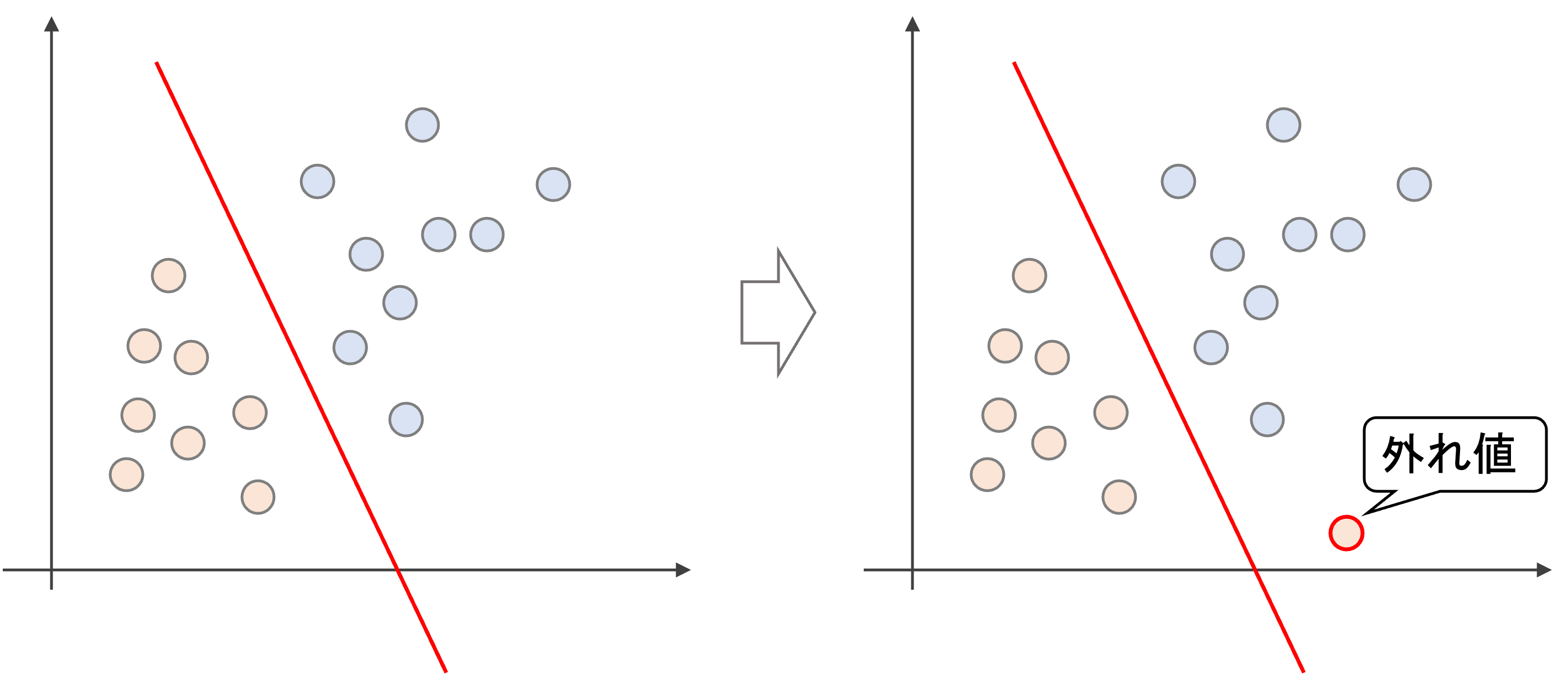
さらにいうと，マージンの中にデータが入り込むことも許容します．

その場合は，より決定境界に近いデータがサポートベクターになるんじゃないの？

そういうわけではないんです．サポートベクターはあくまでもSVMで決定境界を定める過程で決まる物であって，必ずしも決定境界から直近のデータというわけではありません．

SVMでは，マージンを最大化しつつ，誤分類を減らしていくという最適化問題を解いていきます．

マージンの最大はマージンの逆数の最小だと考えると，以下のような最適化を考えることにになります．(まずは厳密な式ではなくイメージのための式をお見せします)

$$min\lbrace\frac{1}{M}+C\sum^{m}_{i=1}\xi_i\rbrace$$

ただし\(M\)はマージン，\(\xi_i\)は\(i\)番目のデータがマージンを侵した具合(つまり残差)を表す変数だと思ってください．また，学習データの総数を\(m\)としています．パラメータ\(C\)を調整することで，どれだけ誤分類を許すかが決まります．

\(C\)が大きいと，\(\xi\)は小さくないといけないので，たくさん誤分類することができなくなります．逆に\(C\)が小さいと，比較的誤分類を許容するようになります．

SVMの損失関数

それでは，実際の損失関数を見てみたいと思います．先ほどの

$$\frac{1}{M}+C\sum^{m}_{i=1}\xi_i$$

という式をもう少し詳しくみてみます．(いきなりこの式をみても，いまいちピンとこないと思うので・・・)

超平面(hyperplane)

まず，超平面というものを理解しましょう．”超”とかついててなんだか難しそうですが，全くそんなことはありません．

超平面(hyperplane)は，2次元空間上の”直線”や3次元空間上における2次元の”平面”を多次元に一般化したものです．

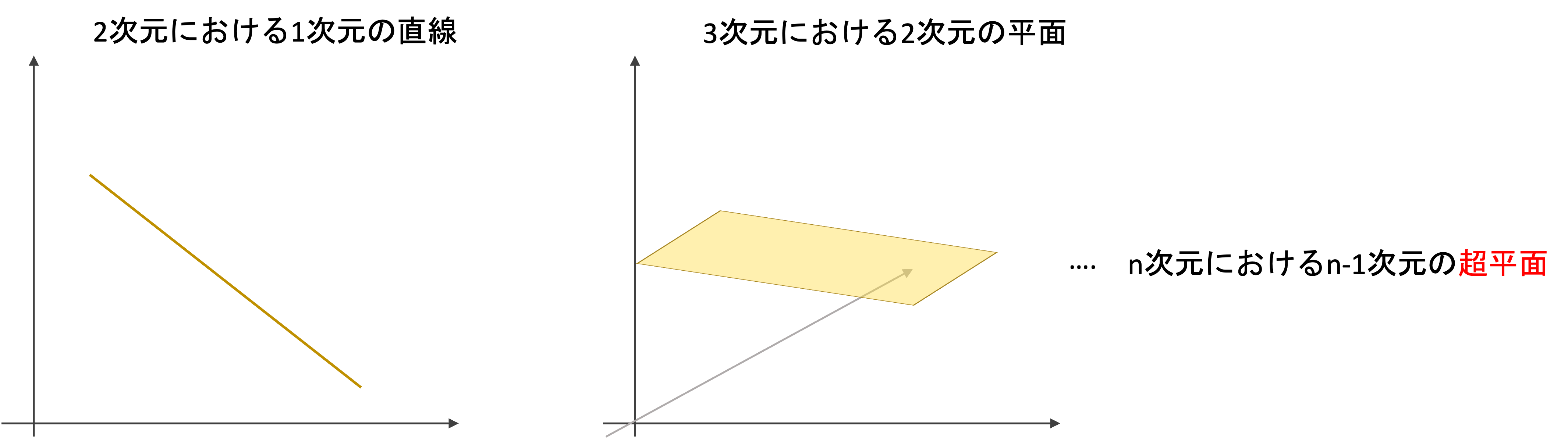
4次元にも同様に3次元の平坦な空間を作れるはずです．しかし，それを”平面”というと語弊があります．そこで，n次元空間内の平坦なn-1次元の集合を超平面と呼びます．ただ呼び方を一般化しただけで，何も難しくありません

一般的な線形分類器の決定境界は，超平面になることがわかると思います．

この超平面の式は第一回で解説している通り，\(\theta_0+\theta_1x_1+\theta_2x_2+\dots+\theta_nx_n=0\)になります．\(x_0=1\)とすると\(\theta_0x_0+\theta_1x_1+\theta_2x_2+\dots+\theta_nx_n=0\)とすることができ，ベクトルで表記すると\(\theta^T\mathbf{x}=0\)と書くことができます．

つまり，未知のデータ\(\mathbf{x}\)に対して\(\theta^T\mathbf{x}\)を計算し，この結果が<0か>0で分類するわけです．

マージン(margin)

SVMでは，サポートベクトルと呼ばれるデータから超平面までの距離をマージン(margin)と呼び，それを最大化することを目的とするんでした．

ここで，ある点\((x_0, y_0)\)から直線\(ax+by+c=0\)までの距離\(d\)は

$$d=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}$$

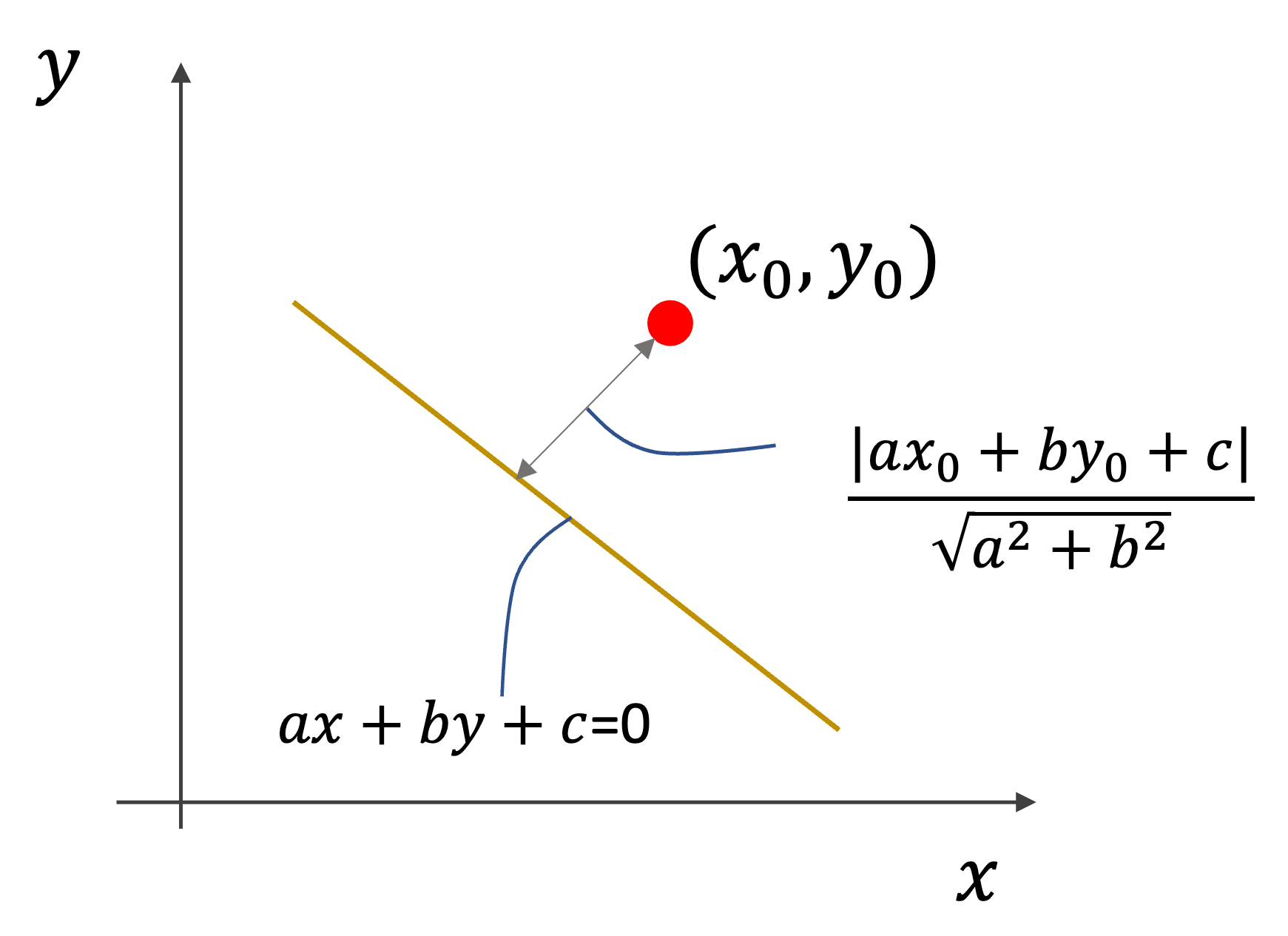
で表されるので，あるデータ\(\mathbf{x}\)から超平面までの距離は同様に

$$d=\frac{|\theta_0+\theta_1x_1+\dots+\theta_nx_n|}{\sqrt{\theta_1^2+\theta_2^2+\dots+\theta_n^2}}$$

であることがわかります．

この距離がマージンとなり，これを最大化するということは，分母である\(\sqrt{\theta_1^2+\theta_2^2+\dots+\theta_n^2}\)を最小化すればいいわけですね．

ここで，数式をシンプルに記述するため，\(\theta_0=0\)としバイアス項を無視します．(バイアス項がある場合は，\(\theta=\theta_1, \theta_2, \dots, \theta_n\)と一つずらせばいいだけです．)また，平方根は扱いにくいので二乗の形にします．

するとこのマージンの最小化は以下のような式に置き換えることができます．

$$min\sum^n_{j=1}\theta_j^2$$

ただし特徴量の数を\(n\)とします．これが「マージンを最大化する」を数式化したものです．

ヒンジ損失

先ほど，「未知のデータ\(\mathbf{x}\)に対して\(\theta^T\mathbf{x}\)を計算し，この結果が<0か>0で分類する」

と言いましたが，SVMではマージンを取ることを考慮し，損失を計算する際に\(\theta^T\mathbf{x}\)が<-1(y=0の時)や>1(y=1の時)の時は損失が0になるようにし，それ以外の場合は線形に損失を増やすということをします．

ん？どういうこと？？

わかるように説明しますね．

第16回で解説したロジスティック回帰の損失関数で紹介したlog lossを思い出してください．

$$-y_ilog\frac{1}{1+e^{-\theta^T\mathbf{x_i}}}-(1-y_i)log(1-\frac{1}{1+e^{-\theta^T\mathbf{x_i}}})$$

これはつまり，以下の二つの損失関数を組み合わせているんでしたね

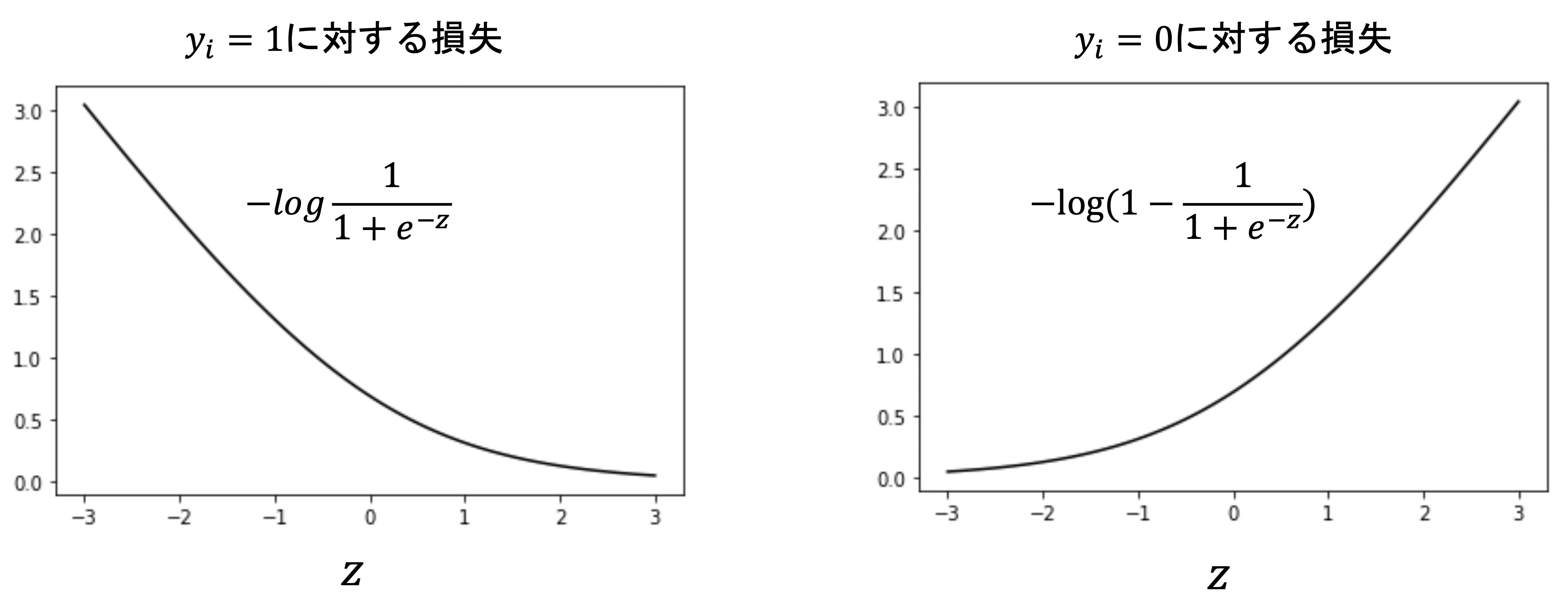
正解ラベルが1であれば，右側の項が0になり上図の左側の損失になり，一方正解ラベルが0であれば，左側の項が0になり上図の右側の損失になるんでしたね．

これを以下の赤線のように近似したのがヒンジ損失(hinge loss)です．

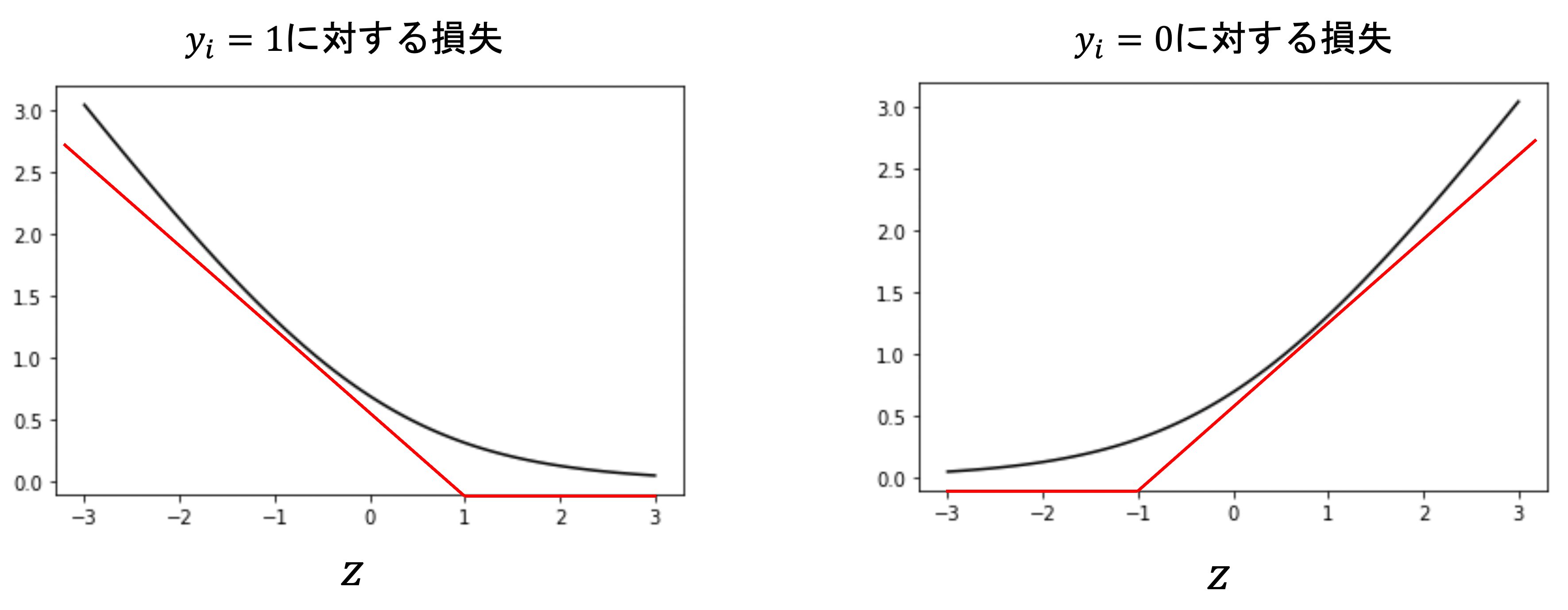
正解ラベルが1のデータにおいては，\(z>1\)(つまり\(\theta^T\mathbf{x_i}>1\))であれば損失0となり，一方正解ラベルが0のデータでは，\(z<-1\)(つまり\(\theta^T\mathbf{x_i}<-1\))であれば損失0となります．

傾きについてはあまり重要じゃないので気にしないでください．このように近似することで，より高速に損失を計算できるようにしています．

このような損失をヒンジ損失(hinge loss)といいます．名前は覚えなくてもいいです．SVMの損失にしか使われないといってもいいくらいなので，さほど重要ではありません．

ポイントは，SVMでは\(\theta^T\mathbf{x_i}\)の結果が，正解ラベルによって<1や>-1で損失が生まれるということです．

つまり，ハードマージンの例では”全て”の\(\mathbf{x_i}\)に対して以下を制約として，\(\sum^n_{j=1}\theta_j^2\)を最小化することを目指します．(ハードマージンでは，マージン内にデータが来ることや誤分類のデータを想定していないため)

$$\theta^T\mathbf{x_i}>1\quad \text{if} \; y_i=1$$

$$\theta^T\mathbf{x_i}<-1\quad \text{if} \; y_i=0$$

ソフトマージン

実際問題では，綺麗に線形分離できないケースがほとんどであり，またそれを目指すと過学習になってしまい結果的に汎化性能が低くなります．

そのため，SVMではマージンの中にデータが入ったり，誤分類することを許容するソフトマージンを採用するのでしたね．

変数\(\xi_i\)を導入して，上記の制約を以下のように緩めます．

$$\theta^T\mathbf{x_i}>1-\xi_i\quad \text{if} \; y_i=1$$

$$\theta^T\mathbf{x_i}<-(1-\xi_i)\quad \text{if} \; y_i=0$$

この\(\xi_i\)と\(\sum^n_{j=1}\theta_j^2\)を組み合わせたのが最終的な損失関数になります．(この損失関数の最適化問題の解き方については，本講座では割愛します．)

$$\sum^n_{j=1}\theta_j^2+C\sum^{m}_{i=i}\xi_i$$

ここで，Cは誤差の正則化項のパラメータであり，モデル構築時に試行錯誤して最適な値を模索する形になります．

ここまでの理論構築が難しく感じる人は，無理して今すぐ理解する必要はありません．

今後SVMを実際に使う時に，もう一度読み返して徐々に理解していきましょう！

カーネルトリック(kernel trick)

さて，今までの理論は全て”線形分離”することを前提に考えていましたが，SVMは”非線形分離”が可能なアルゴリズムです．

これは，カーネルトリック(kernel trick)と呼ばれる手法によって実現させています．

第11回で，特徴量を非線形変換し特徴量を高次元空間に変換することで線形モデルを使って予測する方法を紹介しました．

分類器でも同様にすることで，一見線形分離ができなそうなデータも，高次元特徴量を作ることで線形分離させることができます．

以下はイメージですが，仮に1次元の特徴量\(x\)に対しては線形分離できなくても，\(x^2\)という新たな特徴量空間を作り，\(x\)と\(x^2\)の二次元空間に変換することで，線形分離することができる場合があります．

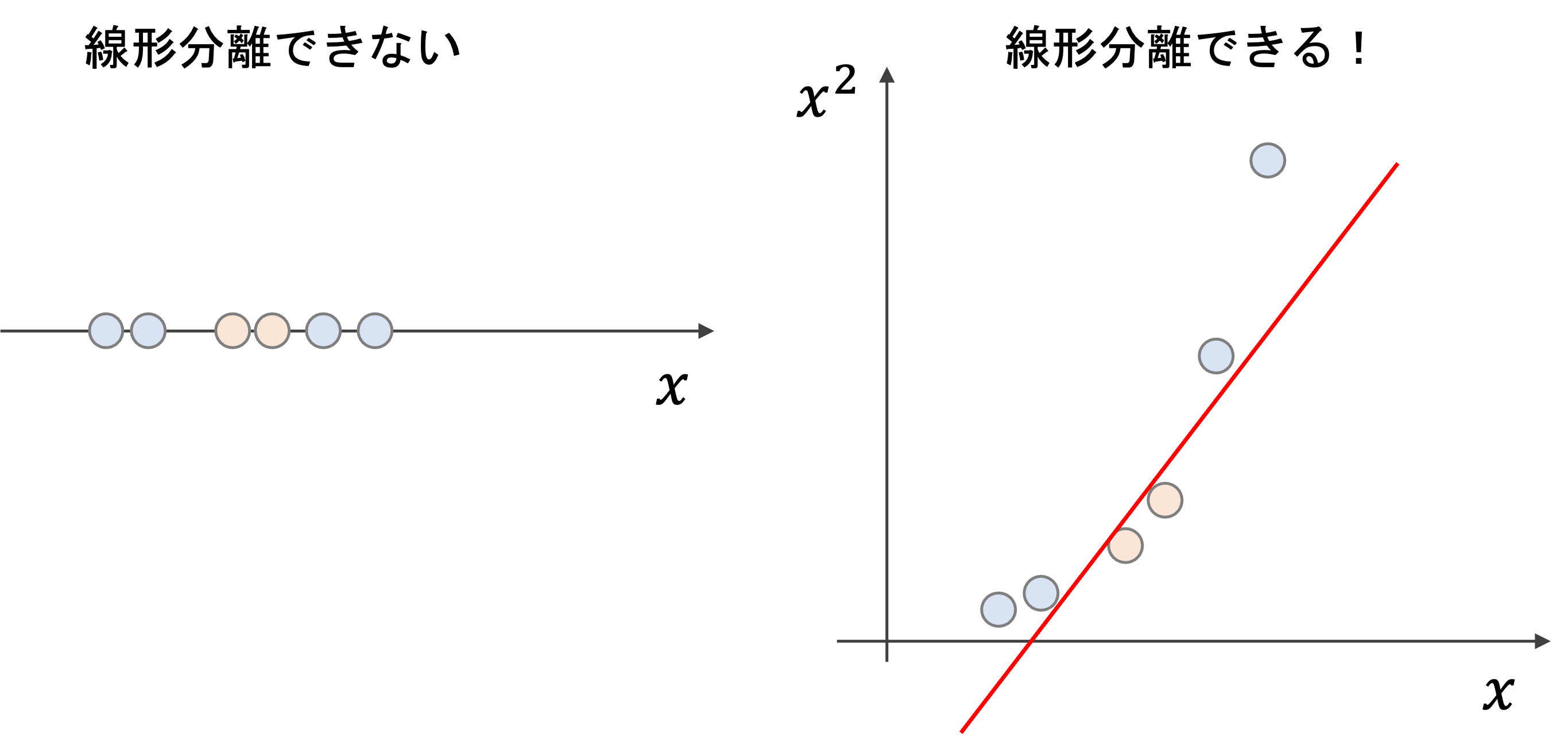
このような変換を写像といいますが，今回の例では\(x\)を\((x, x^2)\)の二次元空間に写像したことになります．一般に，写像する関数を\(\phi(x)=(\phi_1(x), \phi_2(x), \dots, \phi_r(x))\)で表します．

本講座では割愛しましたが，先述したSVMの損失関数を解くうえで，それぞれの学習データ同士の内積\(x_i^Tx_j\)を計算しますが(ただし\(i, j\)は1, 2, …, m)

多次元への変換を行うと，\(\phi(x_i)^T\phi(x_j)\)の計算をする必要がでてきます．

先の例のように，1次元から2次元の変換程度であれば高速にできますが，高次元になると計算量が高くなり計算できなくなってしまいます．

それを解決するのがカーネルトリックです．

\(\phi(x_i)^T\phi(x_j)\)を一つの関数に置き換えることで，計算量を減らします．

$$K(x_i, x_j)=\phi(x_i)^T\phi(x_j)$$

このような\(K(x_i, x_j)\)をカーネル関数といいます．

要は，内積を計算できればいいので，それぞれの変換をしてからそれぞれの内積を計算するのではなく，一発で内積を計算できるようなカーネル関数を使いましょう！ということ

こうすることで，個別の\(\phi(x_i)\)や\(\phi(x_j)\)を計算する必要がなくなり，計算量を抑えることができます．

よく使われるカーネル関数を下に記しておきます．

多項式カーネル

$$K(x_i, x_j)=(x_i^Tx_j+c)^d$$

ガウスカーネル

$$K(x_i, x_j)=exp\lbrace-\frac{||x_i-x_j||^2}{2\sigma^2}\rbrace$$

シグモイドカーネル

$$K(x_i, x_j)=\frac{1}{1+exp(-\gamma x_i^Tx_j)}$$

これらのカーネル関数を使って，SVMのモデルを

$$f(x)=\sum^{m}_{i=1}a_iK(x, x_i)$$

のように，未知のデータ\(x\)に対して全ての学習データ\(x_i\)とのカーネル関数の結果を係数\(a_i\)を使って線形結合した形にします．

式変形を全て記載すると大変なのと，本講座のレベルを超えてしまうので，今回はこういうものだと思ってください．また機会(&要望)があったら，SVMの損失関数の最適化問題の解き方を記事にしたいと思います．

重要なのは，

• SVMはサポートベクターというデータからのマージンを最大化するようにモデルを構築する
• ハードマージンではなくてソフトマージンを採用することで，過学習を防ぐ
• ソフトーマージンではパラメータCを使って，誤差の許容をコントロールする
• 特徴量を高次元空間に変換することで非線形に対応するが，その際にカーネルトリックを使うことで計算量を減らしている

この辺りがわかっていれば，あとはライブラリを使ってSVMでモデルを構築することができるでしょう！！

PythonでSVMを構築する

それでは，PythonでSVMを構築してみましょう．今回は本講座で何度も出てきているirisデータセットを使って３クラス分類器を作ります．

データ準備

今回はsklearn.datasetsを使ってirisデータセットをloadします．

するとNumPy Array形式でXとyが取得できます．yは0, 1, 2のラベルのリストになってます．

これをhold-out法で学習データとテストデータに分割しましょう

SVMでは事前に標準化しておくことが推奨されます．また，今回は描画できるようにするためにPCAを実行します．PCAを実行する前に標準化が必要です．

PCAを実行します．今回は2次元で描画できるようにしたいので， n_components=2 を指定します．

モデル学習

SVMには， sklearn.svm.SVC クラスを使います．使い方は今まで扱ってきたscikit-learnの他のモデルと同じです．（ちなみに，回帰には skleawrn.svm.SVR を使います．）

他のモデル同様，インスタンス生成時にパラメータを指定します．ここではよく使うパラメータについて簡単に解説しておきます！

• C : 誤差の正則化項の係数．デフォルトは1
• kernel : 使用するカーネル関数を 'linear' , 'poly' , 'rbf' , 'sigmoid' , 'precomputed' から選択.デフォルトは 'rbf'
  • 'linear' : \(x_i^Tx_j\)
  • 'poly' : \(\gamma(x_i^Tx_j+r)^d\)
  • 'rbf' (Radial Basis Function): \(exp(-\gamma||x_i-x_j||^2)\)
  • 'sigmoid' : \(tanh(\gamma x_i^Tx_j+r)\)
  • 'precomputed' を指定した場合は自分で X を変換して .fit させます
• degree : 'poly' を選択したときのdegree \(d\). デフォルトは3
• gamma : 'poly' , 'rbf' , 'sigmoid' の係数\(\gamma\). 'scale' (デフォルト)を指定すると\(\frac{1}{n\times Var(X)}\). 'auto' を指定すると\(\frac{1}{n}\)(ただし\(n\)は特徴量の数)

今回は kernel='linear' を指定してモデルを作ります．

予測と評価

他のモデルと同じように， .predict() や .predict_proba() で予測値を出すことができます．

サポートベクトルの可視化

では，実際にどのデータがサポートベクトルとして使われたのかを見てみましょう．

やたらと多いように思いますが，これらはマージン内に侵しているデータや，誤分類しているデータも含みます．

このままだとわかりにくので，決定境界とともに可視化してみましょう！

以下のようにSVMが作る決定境界と，学習データおよびサポートベクトルを描画します．

コードの詳細な説明は本記事では割愛しますが，パラメータ名を見れば簡単に理解できると思います．

なお，モデルの決定境界を描画するには sklearn.inspection.DecisionBoundaryDisplay.from_estimator 関数が便利です．version 1.1から利用可能なので，古いバージョンのscikit-learnを使っている場合は最新版に更新してください．( pip install --upgrade scikit-learn で更新できます．jupyterで実行する場合は % をつけましょう)

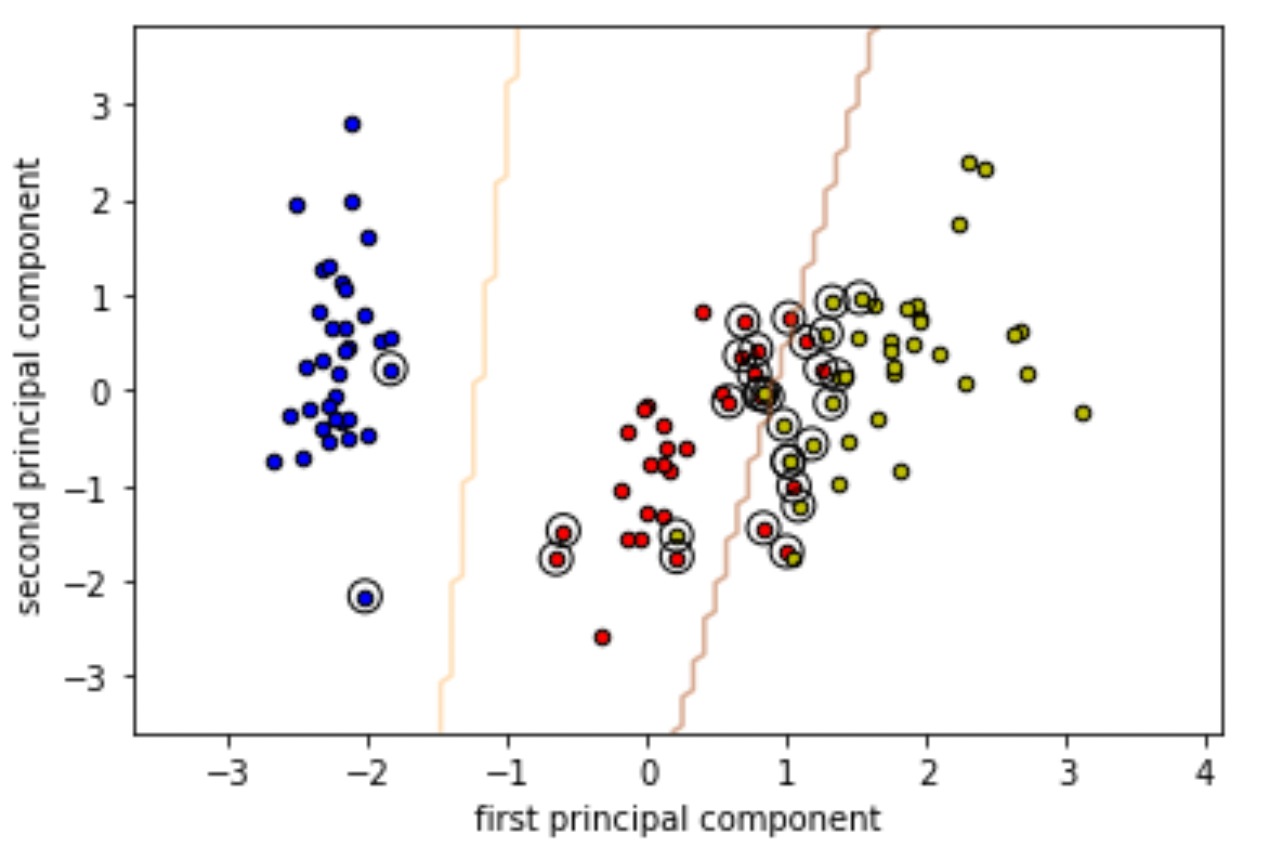
境界線の周りのデータ及び，誤分類しているデータがサポートベクトルになっているのがわかると思います．

コードがよくわからない人は，とりあえずコピペしましょう笑

描画のコードがよくわからない！という方は是非↓の講座でPythonのライブラリの学習をしてください．☆4.8でUdemyで最も評価が高い講座になっています．

【公開初日で受講生1000人超え！】データサイエンスのためのPython動画講座を公開しました【全23時間…!!】

これを使って，パラメータを色々と変更したらSVMの決定境界やサポートベクターがどうなるのかをみてみてください．

例えばパラメータCを大きくすると，マージンが小さくなりサポートベクターの数が減っていくのがわかると思います．

また，kernelや他のパラメータを変更したらどのように決定境界が変化していくのかがわかります．

興味がある人はやってみてください！

まとめ

今回もかなり長くなってしまいましたが，まとめです．

今回はSVM(サポートベクターマシン)について解説しました．

• SVMは単体のモデルではかなり精度が高く一時は一世を風靡したほど．今でもよく使用される
• SVMはサポートベクターと決定境界の間(マージン)を最大化する
• マージンの中にデータが入ったり，誤分類することを想定するソフトマージンを採用することで，線形分離できないデータセットにも対応し，過学習を避ける
• 誤差の正則化項の係数Cを調整することで，マージンの幅を調整する
• 特徴量空間を高次元空間にすることで非線形の決定境界を作り，非線形なモデルを構築できるようにしている
• 高次元の特徴量空間への変換の際に，カーネル関数を使うことで高速に最適化問題を解けるようにしている(カーネルトリック)

SVMについてはまだまだ話したいことはたくさんあるのですが，記事が長くなってしまうので，本講座では本当に重要な内容のみを厳選しました．

なので本記事で書いた内容は“SVMを使うなら全て知っておくべき内容”です．

是非何度も読み返して理解できるようにしましょう！

それでは！

次回(最終回)の記事書きました！！　次回は最適なモデルとそのハイパーパラメータを見つける方法を紹介します

最適な機械学習モデルを探索する(Pipeline+Grid Search)【機械学習入門35】