多項式特徴量で線形を超える！【機械学習入門11】

こんにちは，米国データサイエンティストのかめ(@usdatascientist)です．

データサイエンス入門の機械学習編第11回です！(講座全体の説明と目次はこちら)

追記)機械学習超入門動画講座を公開しました！動画で効率よく学習をしたい人はこちら(現在割引クーポン配布中です)

今回の記事では，多項式特徴量というものを紹介します．

今までの記事では全て線形モデルを使って解説をしていましたが，線形モデルは解釈がしやすい分「線形」という制約があるため精度に限界があります．

多項式特徴量というものを使って，線形モデルを簡単に非線形にすることができます．できる幅が広がるのでしっかり押さえておきましょう！

1 線形モデルの限界
2 多項式特徴量(多項式回帰)
3 Pythonで多項式回帰を実装する
4 交互作用項について
5 まとめ

線形モデルの限界

下の図をみてください．

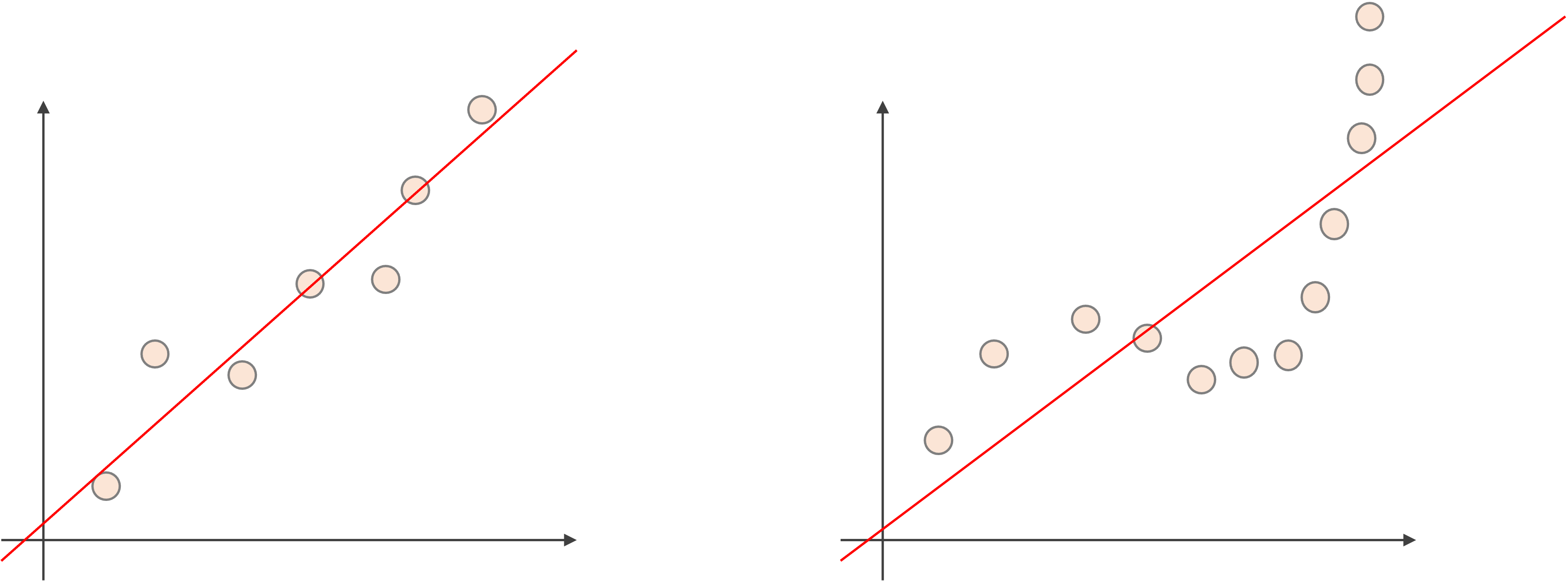
左図のように，データの分布がある程度線形であれば線形モデルを使ってそこそこ精度の高いモデルを構築することができますが，右図のように明らかに線形関係がみられないようなデータでは，どんなに頑張って線形モデルを構築しても精度の高いモデルを構築するのは不可能です．(だってそもそも線形じゃないんだからね！)

実際の問題では，真の$f(x)$が線形($f(X)=\theta_0+\theta_1X_1+\theta_2X_2+\cdots+\theta_nX_n$)であるほうが珍しいので，「まさか線形のはずはない」と考えるのが普通でしょう．

では，どのようなモデルを仮定するのか？

これには色々とありますが，大きく分けて以下の二つです

非線形アルゴリズムを使う
特徴量を非線形変換する

非線形アルゴリズムには色々な種類があります，今後の記事で紹介予定のKNNやSVM，深層学習のモデルなんかはいずれも非線形アルゴリズムです．

これらについては今後の記事で詳しく紹介していきます．

もっと簡単にできる「特徴量を非線形変換する」やり方のうちの一つが「多項式特徴量」です．

多項式特徴量(多項式回帰)

多項式特徴量(Polynomial Features)はその名の通り，特徴量を多項式にします．例えば$X_1$を$X_1^2$にしたり$X_1^3$にします．

多項式回帰(Polynomial Regression)なんて呼び方もしますが，使用するモデルは以下です．

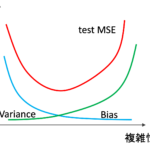
$$y_i=\theta_0+\theta_1x_i+\theta_2x_i^2+\theta_3x_i^3+\cdots+\theta_dx_i^d+\epsilon$$

実際には3を超える$d$を使うことはほとんどないと思います．

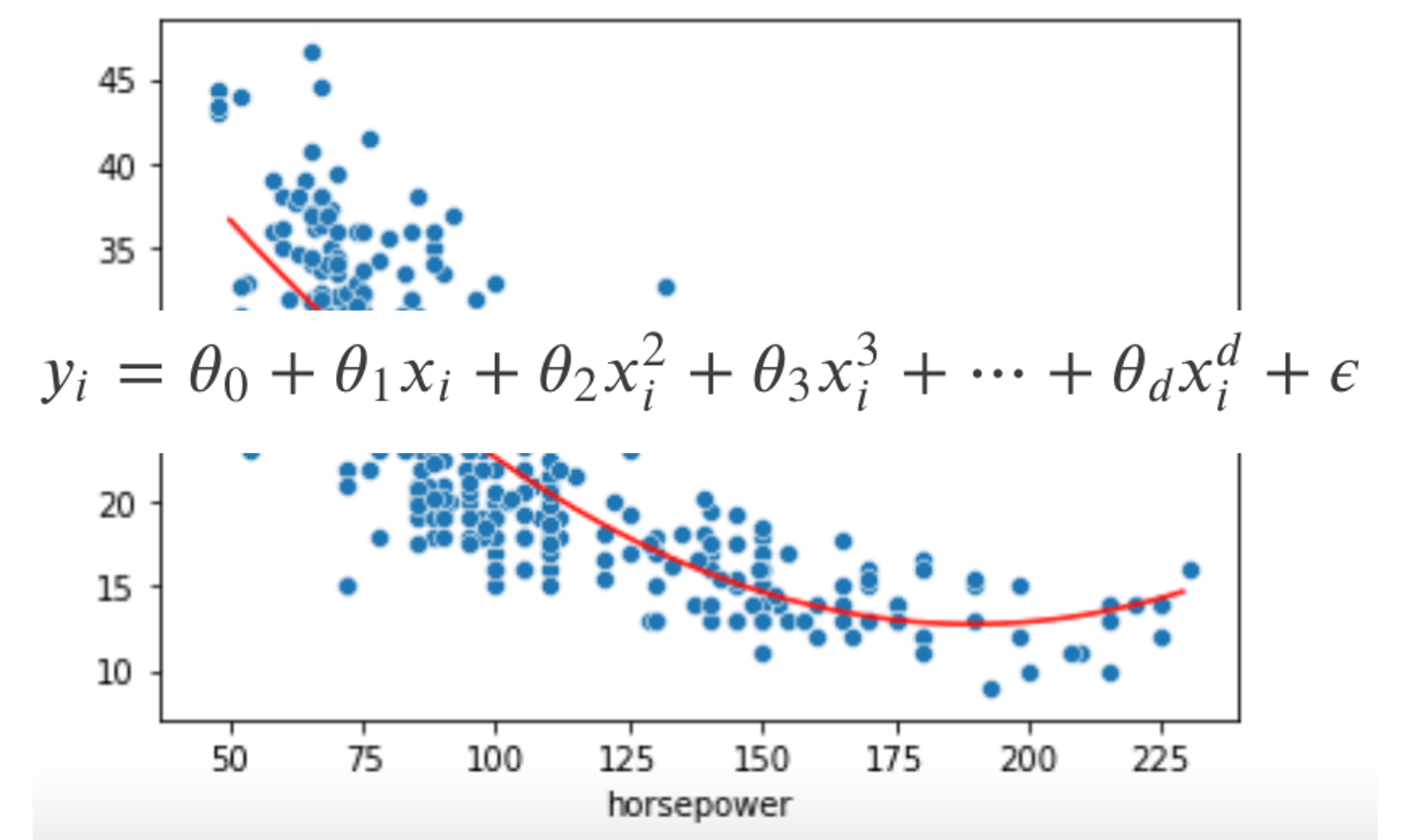
例えば以下は，線形回帰モデルと多項式回帰モデル(d=2)を使った結果です．(後ほどPythonでの実装で実際に描画してみます)

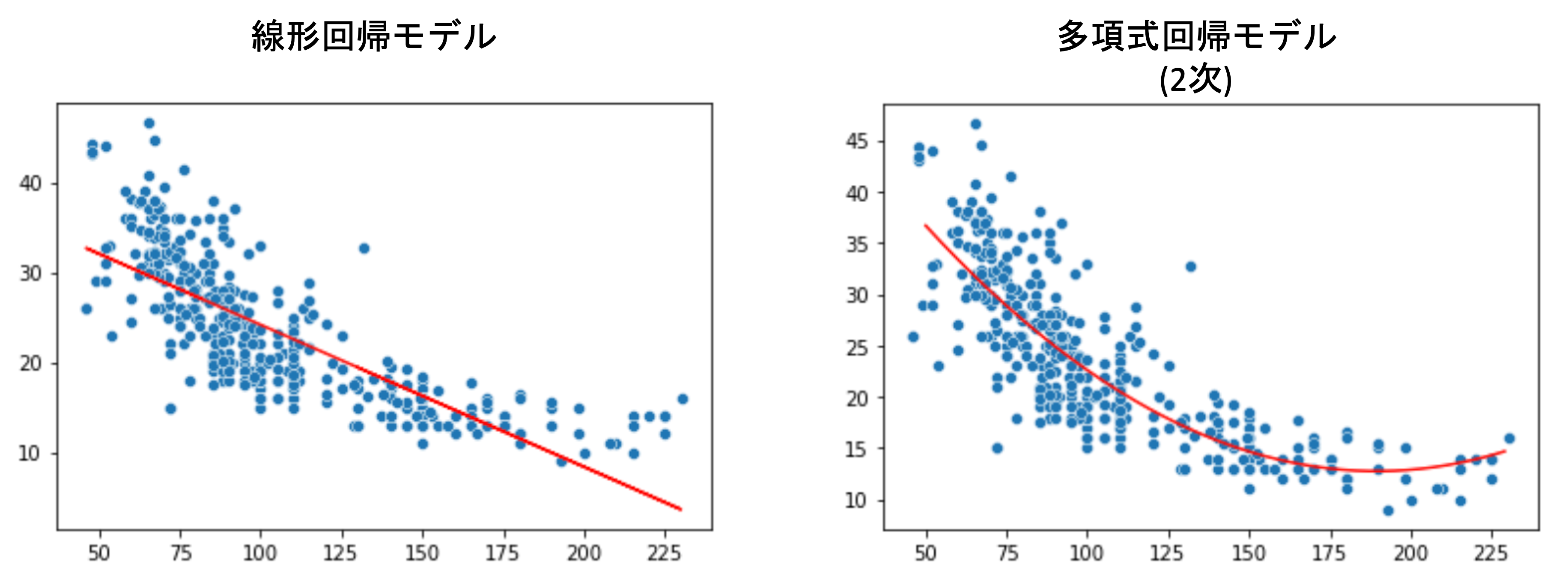
線形ではないデータに対してはぱっと見有効そうであることがわかると思います．

それでは実際にPythonを使って多項式回帰モデルを実装して結果をみてみましょう！

補足
多項式回帰はあくまでも線形モデルであることに注意しましょう.これは，$x$という特徴量と$x^2$という別の新たな特徴量と考えると，これらは線形回帰モデルに適用できることがわかると思います．なので，多項式回帰モデルは結果をplotすると非線形のように見えますが，これを”非線形モデル”と呼ばないことに注意しましょう．（非線形に見えるのは，x軸にもとの$x$を指定しているからです．これを$x$の軸と$x^2$の軸の二つを用意したら，平面になり線形回帰の結果と同じようになりますよね？）

Pythonで多項式回帰を実装する

多項式回帰は，特徴量の変換とみることができるので，処理としては”前処理”の分類に入ります．

scikit-learnには前処理用の preprocessing モジュールが用意されています

多項式回帰は， preprocessing モジュールの中に用意されていて(統計学講座第9回でやった標準化も同じです) PolynomialFeatures クラスを使います．

PolynomialFeatures クラスのインスタンス化時には主に以下の引数を入れます．

degree : 次元. 上述した式の$d$.
interaction_only : 多項式を作った際に，複数の特徴量がある場合$x_1, x_2, x_1x_2, x_1^2, x_2^2$のように交互作用項(これについては後述)も作られるが，Trueにすると交互作用項のみ$x_1, x_2, x_1x_2$が使われる（デフォルトではFalse）
bias : バイアス項を入れる(バイアス項というのは切片に対応する項のこと) (デフォルトではTrue)

インスタンス生成後， .fit_transform() メソッドに元の特徴量 X を入れて新たな特徴量(多項式特徴量)を生成します．この辺りはコードをみて実行して中身を見たほうが早いでしょう！

今回はmpgデータセットを使います．mpgはmiles per gallonの略で，車のスペックとmpgを記録したデータセットです．mpgデータセットを使ってhorsepower(馬力)からmpgを予測するモデルを例にしていきます．

import seaborn as sns
df = sns.load_dataset('mpg')
df.dropna(inplace=True)
X = df['horsepower'].values.reshape(-1, 1)
y = df['mpg'].values

import seaborn as sns

df = sns.load_dataset('mpg')

df.dropna(inplace=True)

X = df['horsepower'].values.reshape(-1, 1)

y = df['mpg'].values

scatter plotを描画してみると

import matplotlib.pyplot as plt
sns.scatterplot(df['horsepower'], df['mpg'])

1 2	import matplotlib.pyplot as plt sns.scatterplot(df['horsepower'], df['mpg'])

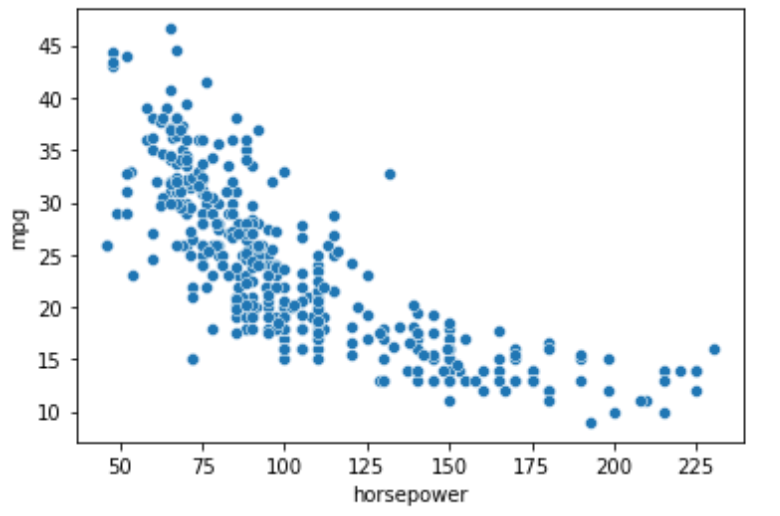
こんな感じで，馬力が大きくなるにつれて燃費が悪くなっているのがわかります．これは当然ですよね．ただ，その関係は単純な線形ではなく，馬力の増加に対して燃費の減少が緩やかになっているのがわかると多います．

こういうデータに対しては，単純な線形回帰ではなく多項式回帰が有効そうです．

PolynomialFeatures クラスを使って多項式特徴量に変換します．今回はd=2でやってみます．

from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(2)
X_poly = poly.fit_transform(X)
X_poly

from sklearn.preprocessing import PolynomialFeatures

poly = PolynomialFeatures(2)

X_poly = poly.fit_transform(X)

X_poly

すると，もとの$x$だけではなくバイアス項と$x^2$ができた状態になっているのがわかります．

それではいつも通り LinearRegression() を使って線形回帰アルゴリズムでモデルを学習しましょう．

from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_poly, y)
model.coef_

from sklearn.linear_model import LinearRegression

model = LinearRegression()

model.fit(X_poly, y)

model.coef_

array([ 0.        , -0.46618963,  0.00123054])

1	array([ 0. , -0.46618963, 0.00123054])

すると，三つの係数が返ってきます．これはそれぞれ，1, $x$, $x^2$に対する係数です．今回はバイアス項も含めた形で .fit() したので，特徴量として学習されてしまいましたが，係数が0になっているので本来のバイアス項の存在により結果的に落とされた形になります．

補足
普通， .fit() に入れる X にはバイアス項を含める必要はありません．なので， PolynomialFeatures() には bias=False を指定してバイアス項を生成しなくていいです．が，バイアス項があったとしても係数が0になるので問題ありません．

それでは，描画をしてみましょう．今回はx軸の値を新たに作り，同様に fit_transform() してから .predict() します．

import numpy as np
# X軸の値作成
x = np.arange(50, 230).reshape(-1, 1)
# .predictの前に同様にfit_transformする必要があることに注意
x_ = poly.fit_transform(x)
pred_ = model.predict(x_)
# 描画
sns.scatterplot(df['horsepower'], df['mpg'])
plt.plot(x, pred_, 'r')

import numpy as np

# X軸の値作成

x = np.arange(50, 230).reshape(-1, 1)

# .predictの前に同様にfit_transformする必要があることに注意

x_ = poly.fit_transform(x)

pred_ = model.predict(x_)

# 描画

sns.scatterplot(df['horsepower'], df['mpg'])

plt.plot(x, pred_, 'r')

補足
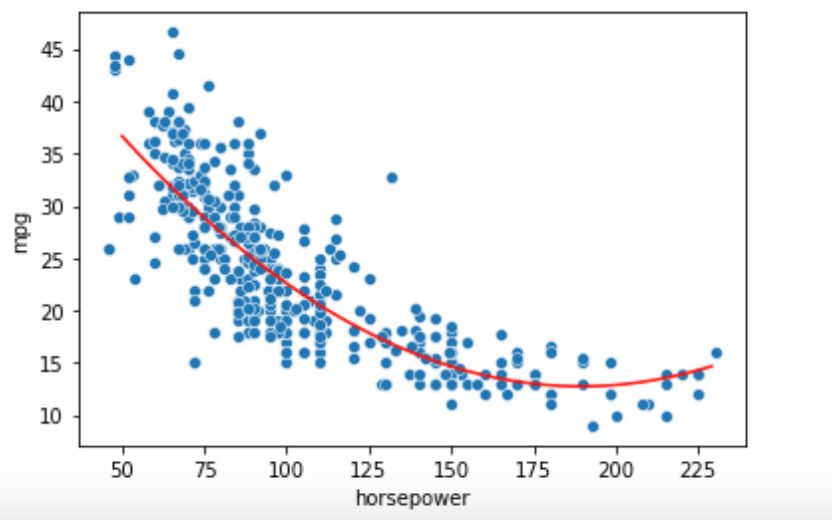
特徴量の変換など，学習時に前処理をした場合はテストデータに対しても同様に前処理をする必要があることに注意しましょう

興味がある人はd=3やそれ以上の場合でやってみてください． PolynomialFeatures()の degree 引数を変えるだけでOKです．

交互作用項について

今回紹介した例では特徴量が一つのみだったので，$y_i=\theta_0+\theta_1x_i+\theta_2x_i^2+\theta_3x_i^3+\cdots+\theta_dx_i^d+\epsilon_i$というモデルを考えましたが，特徴量が複数ある場合(例えば$X_1, X_2$)は

$$y_i=\theta_0+\theta_1X_1+\theta_2X_2+\theta_3X_1^2+\theta_4X_2^2+\theta_5X_1X_2+\epsilon$$

のような形をとることがあります．$X_1X_2$は交互作用項(interaction term)と呼ばれ，単体ではなくて相互に関係のある特徴量とし，多項式特徴量のみならず交互作用項も組み合わせることがあります．

例えばマーケティングをする際に，TV広告への投資と動画配信サイトの広告への投資をそれぞれ単独に行った時の売り上げよりも，これらを組み合わせることで相乗効果によりさらに売り上げが上がるようなデータであれば，交互作用項も有効と考えられます．

本講座では交互作用項についてはここまでとしますが，考え方は多項式特徴量と同じです．また，交互作用項を作る際は例えp値が低くてもそれぞれ単独の特徴量を含む形でモデルを構築するのが普通なのでその辺りは覚えておきましょう．

PolynomialFeatures()クラスではこの交互作用項も含む形で特徴量変換が行われることも頭に入れておくといいです．

まとめ

今回の記事では，特徴量を非線形に変換する方法の一つとして多項式特徴量(多項式回帰)について解説をしました．

特徴量と目的変数が線形の関係にない場合，線形回帰では精度に限界がある
特徴量$x$を$x^2$や$x^3$のように多次元にして線形回帰を行うことを多項式特徴量や多項式回帰という
sklearn.preprocessing.PolynomialFeatures()クラスを使うことで簡単に特徴量を多項式変換することができる(特徴量が複数ある場合は交互作用項も作られる)
特徴量に変換を行なって学習した場合，評価時にもデータに対して同様の変換が必要であることに注意する

多項式特徴量は，気軽に非線形の関係をモデリングできるシンプルな方法でかつ解釈もしやすいのでよく使われます．

普通，多項式特徴量の次元を高くすればするほど，モデルは複雑になり，学習データに対してよくフィットするようになります．

じゃぁどれくらい多次元にするのがいいのか？複雑にしすぎるとなにが起こるのか？

これについては次回の記事で解説したいと思います．機械学習で最も重要な概念の一つである”Bias-Variance Tradeoff”の話になってくるので，必ず次も学習を進めてください！

それでは！

追記)次回の記事書きました．本講座でも最も重要な回のうちの一つです．必ず読んで欲しいです．