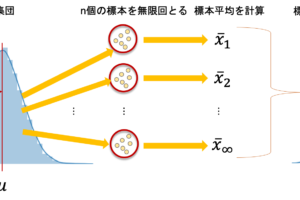
統計講座も第27回まできました.30回は超えますね,確実に
(追記)全16時間の統計学動画講座を公開しました!☆4.8の超高評価をいただいている講座です.こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください.
前回までは推測統計の”推定”について話を進めてきましたが,今回から“検定”を扱っていきます.(推定と検定についてはこちらの記事で概要を書いております)
まず検定について話をする前にこれだけ言わせてください...
“検定”こそが統計学を学ぶ一番のモチベーションであり,統計学理論において最も重要な役割を果たしている分野である
つまり,今までの統計学講座もこの”検定”を学ぶための準備だと思ってください.(それは言い過ぎ?でも,それくらい重要な分野なんです)
じゃぁ,”検定”でどんなことができるのか?そのやり方について今回は詳細に解説していきます.
(今回は理論的な話ばかりになってしまいますが,次回以降実際にPythonを使って検定をやっていくのでお楽しみに!)
検定ってなに?
簡単にいうと「ある物事の想定に対して標本観察によりその想定が矛盾するのかどうかを調べること」です.

具体例で見ていきましょう!
例えばある工場で製品を作っていて,ある一定の確率で不良品が生産されてしまうとしましょう.
この不良品が出てしまう確率を下げるべく,工場の製造過程を変更することを考えます.
この変更が実際に効果があるのかどうかを判断するのに役立つのが”検定”です.
変更前と変更後の製品の標本をとってみて,もし変更後の方が不良品がでる確率が少なければ,「この変更は正解だった」と言え,工場の生産過程を新しくすることができそうです.
仮にそれぞれ100個の製品の標本を取ったとき,変更前の過程で生産された製品100個のうち不良品が5個で,変更後の不良品が4個だったとしましょう.
確かに今回の標本では改善が見られますが,これを見て実際に「よし,工場の生産過程を変えよう!」って思えますか?
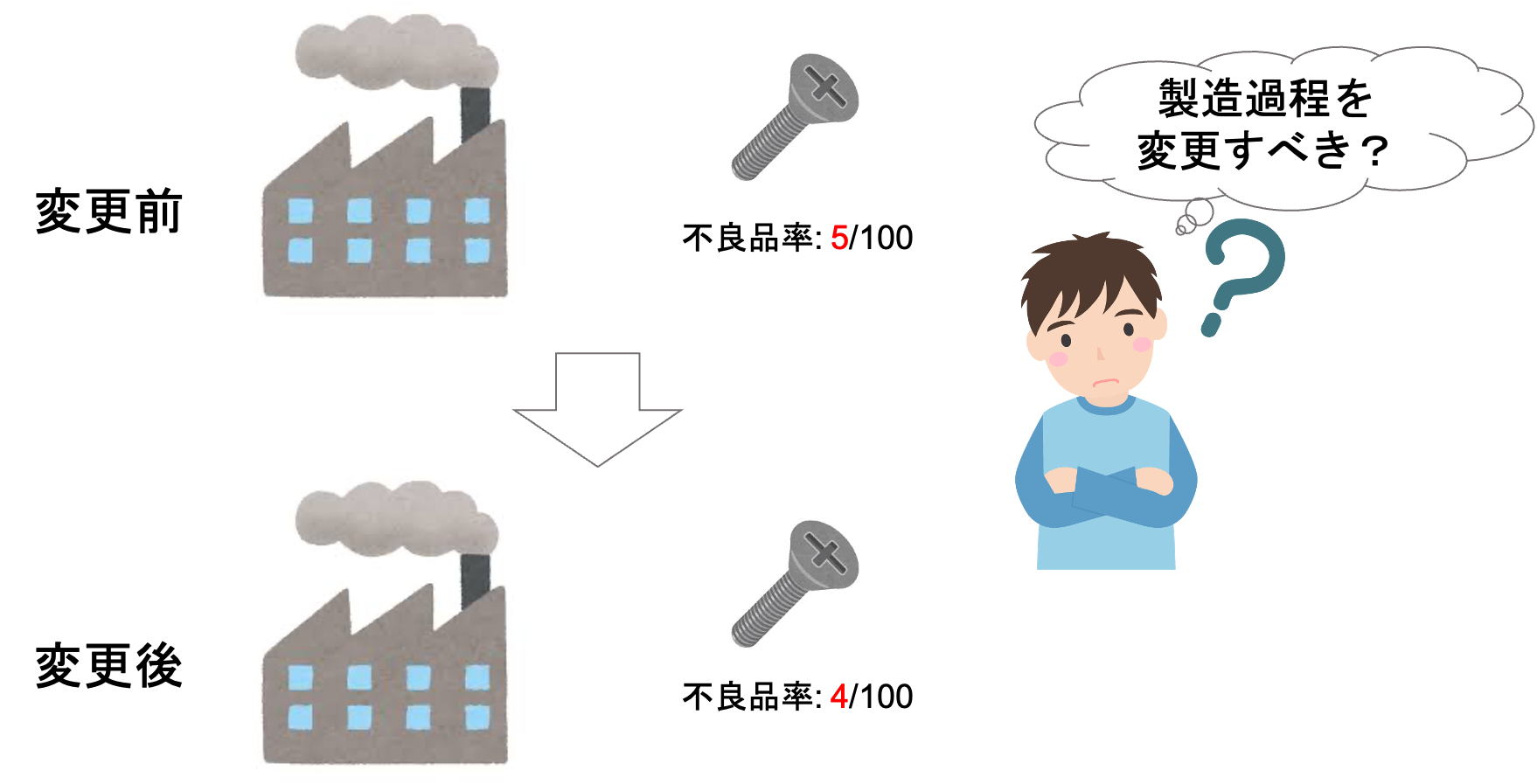
じゃぁこれが変更後の不良品が3個だったら?2個だったら?2個だったら生産過程を新しくしてもよさそうですよね.
このような判断が必要な場面で出てくるのが検定です.つまり検定は意思決定を左右する非常に重要な役割を果たすわけです.
では,どのように検定を使うのか?
まず,「変更前と変更後では不良品が出る確率は変わらない」という「想定」をします.
この想定の元,標本から計算した不良品率(比率ですね!)を見た時にありえない(=想定が正しいとは言い難い)数字が出た場合,「想定が間違ってるんじゃない?」と言えるわけです.つまりこの場合,「変更前と変更後で不良品が出る確率が違う」ということが言えるわけですね.これを応用して,生産過程を変更するかどうかを判断できるわけです.
この想定のことを“仮説”(hypothesis)といい,仮説を使った検定ということで,検定のことを統計的仮説検定と言ったりもします.
もう少し専門用語を交えて,統計的仮説検定の流れを説明していきます!
統計的仮説検定の流れ(帰無仮説と対立仮説)
統計的仮説検定の基本的な流れは
- 仮説を立てる
- 仮説のもと標本観察を行う(標本統計量を計算する)
- 標本観察の結果,仮説が正しいといえるかどうかを調べる
統計的仮説検定のポイントは,「最初に立てた仮説は否定することを想定して立てる」ということ.
つまり,「おそらくこの仮説は間違ってるだろうな〜」と思いながら仮説を立てるわけです.標本観察する際に「この仮説は間違ってるんじゃない?」って言えるようにしたいわけです.
例えば先ほどの例では,「変更前と変更後では不良品が出る確率は変わらない」という仮説を立てたわけですが,心の中では「変更前と変更後では不良品が出る確率が同じなわけないよね??」って思ってるわけです.
最初から否定することを想定して立てている仮説なので,この仮説のことを帰無仮説(null hypothesis)と呼びます.重要な用語なので覚えておきましょう.(無に帰すことがわかってるので帰無仮説…なんとも悲しい仮説ですね)
一方帰無仮説が否定された場合に成立する仮説を対立仮説(alternative hypothesis)と言います.
例えば「変更前と変更後では不良品が出る確率は変わらない」という帰無仮説を標本観察の結果否定した場合,「変更前と変更後では不良品が出る確率は異なる」という新しい仮説が成立します.この仮説が対立仮説です.つまり,心の中で正しいと思っている仮説が対立仮説です.

なので先ほどの手順をもう少し専門用語を用いて言い換えると
1.帰無仮説と対立仮説を立てる
2.帰無仮説のもとで標本観察を行う(標本統計量を計算する)
3.標本観察の結果,帰無仮説を否定できるかどうかを確認する(否定した場合,対立仮説が成立する)

と,思う人も多いかと思いますが,最初から対立仮説を立ててそれを肯定するというのは難しいんです.
今回の例では「変更前と変更後では不良品が出る確率は異なる」ことを言いたいんですが,これって色々なケースが考えられますよね?
「変更前と変更後で不良品率が1%違う」とか「変更前と変更後で不良品率が1.3%違う」とか
無限にケースが存在します.
なのでこれを成立させるにはただ一つ「変更前と変更後では不良品が出る確率が同じ」ということを否定すればOKということになります.
逆にいうと,「変更前と変更後では不良品が出る確率は異なる」のような無限にケースが考えれられるような仮説を帰無仮説にすることもできません.
この辺りは実際に検定をいくつかやって慣れていきましょう!
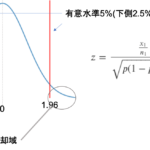
棄却域と有意水準
では,帰無仮説を否定するにはどうすればいいのでしょうか?
これは,帰無仮説が成り立つという想定のもと標本から統計量を計算して,その統計量が帰無仮説が正しいとは言い難い領域(つまり帰無仮説が正しいとすると,その統計量の値が得られる確率が非常に小さい)かどうかを確認し,もしその領域に統計量が入っていれば否定できることになります.
この領域のことを棄却域(regection region)と言います.(反対に,そうではない領域を採択域(acceptance region)と言います.この領域に標本統計量が入る場合は,帰無仮説を否定できないということですね)
そして,帰無仮説を否定することを棄却する言います.
では,どのように棄却域と採択域の境界線を決めるのでしょう?
標本統計量を計算した時に,帰無仮説が成り立つと想定するとどれくらいの確率でその値が得られるかを考えます.
通常は1%や5%を境界として選択します.つまり,その値が1%や5%未満の確率でしか得られない値であれば,帰無仮説を棄却するわけです.
つまり,棄却域に統計量が入る場合は,たまたま起こったのではなく,確率的に棄却できるわけです.
このように,偶然ではなく意味を持って帰無仮説を棄却することができるので,この境界のことを有意水準と言いよく\(\alpha\)で表します.
1%や5%の有意水準を設けた場合,仮に帰無仮説が正しくてたまたま1%や5%の確率で棄却域に入ったとしても,もうそれは意味の有る原因によって棄却しようということで,これを有意(significant)と言ったりします.
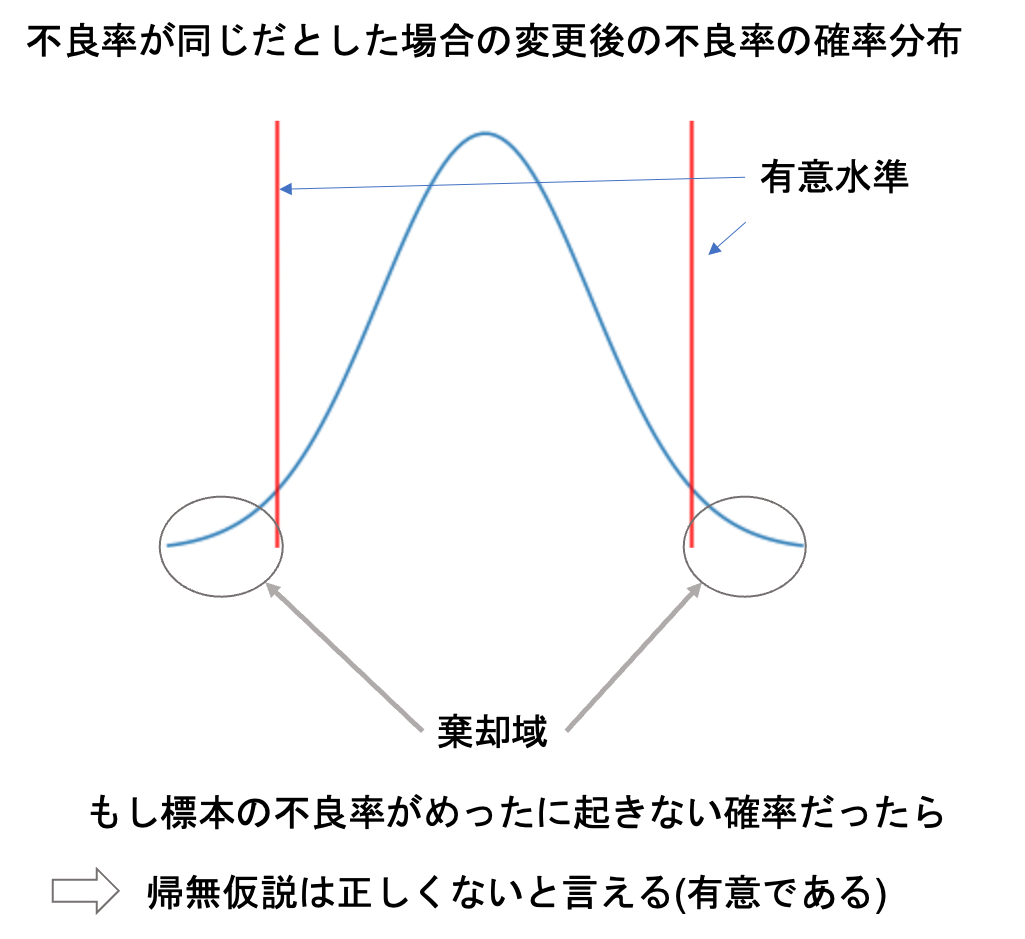
この辺りの用語は今はあまりわからなくてもOK! 今後実際に検定をしていくと分かってくるはず!
なにを検定するのか

検定は色々な種類があるのですが,本講座では有名なものだけ扱っていきます.(「とりあえずこれだけは押さえておけばOKでしょ!」というものだけ紹介!)
1. 比率の差の検定
先ほどの例はまさにこれですね.ある工場の製造過程変更前と後で不良品率(比率)に差があるかを検定によって調べたのでした.
他にも,
- マーケティングのある施策によってダイレクトメールから自社サイトにアクセスする割合は変わったかどうか
- 日本の30代男性の既婚率と米国の30代男性の既婚率とでは差があるのか
などなど,様々な例が考えられます.
2. 連関の検定
カテゴリ変数の相関のことを連関(association)と言います.(相関については第11回あたりで詳しく解説しています)
例えば「Pythonを勉強してる人ほどRを勉強しているのか」などです.
Pythonを勉強しているか否かは2値のカテゴリ変数です.同様に,Rを勉強しているか否かも2値のカテゴリ変数ですよね.
カテゴリ変数の場合は第11回で解説した相関は計算できません.相関ではなく連関とよび,それを計算する手法があります.(今後の講座で扱っていきます.)
この連関の有無を検定によって調べることができます.仮説検定の中でもよく使われる検定です.使用する統計量がカイ二乗(\(\chi^2\))統計量をベースにしているものが多いため,カイ二乗検定と言われたりもします.この辺りは今後の講座で詳しく解説していきます!
3. 平均値差の検定
平均に差があるのかを検定します.比率の差の検定があったら,平均の差の検定もありそうですよね!
例えば
- 工場Aと工場Bの製品の誤差の平均は等しいのか
- 東京都と大阪府の小学生の1日の平均勉強時間は等しいのか
- 試薬Aと試薬Bで効果は等しいのか
などです.
平均値差の検定にはt分布を用いるので,t検定(Student’s t-test)とも呼ばれます.こちらもよくビジネスやサイエンスの現場で本当によく使う検定です.(t分布については前回の記事で詳しく解説してます.)
(また講座で詳しくやりますが,)t検定はそれぞれの群の分散が正しいことを前提にしています.
なので,場合によっては「分散が正しいと言えるのか」という検定をあらかじめ行う必要があったりします.(分散が異なる場合は高度な検定手法が必要になりますが,本講座では扱いません.)
4. 分散の検定
二つの母集団の分散が異なっているかどうかを検定します.

統計学の理論では「二つの母集団の分散が正しいことを仮定する」ケースが多いです.先ほどのt検定もその一つです.
比率の検定,連関の検定,平気値差の検定ほど出番はないかもしれませんが,分散の検定も学習しておく基本的な検定の一つなので,今回の講座で扱っていきたいと思います!
まとめ
今回の記事では,統計的仮説検定の流れと用語,種類について解説をしました.
- 統計的に正しい判断をするために検定が利用される.検定は統計学で最も重要な分野の一つ.
- 統計的仮説検定では,仮説を立てて,その仮説が正しいという仮定のもとで標本統計量を計算して,その仮説が正しいといえるかどうかを統計的に判断する
- 最初に立てる仮定は否定することを前提にし.これを帰無仮説と呼ぶ.一方帰無仮説が否定されて成立される仮説を対立仮説と呼ぶ
- 統計量を計算し,それが帰無仮説の仮定のもと1%や5%(有意水準)の確率でしか起こり得ないものであればこれはたまたまではなく”有意”であるとし,帰無仮説を否定(棄却)する
- 検定には色々な種類があるが,有名なものだと比率差の検定,連関の検定,平均値差の検定,分散の検定がある.
検定は統計学の山場です.
今までの統計学の理論は全てこの”統計的仮説検定”を行うためのものと言っても過言ではありません.
これから詳細に解説していくので,しっかり学習していきましょう!
追記)次回書きました!