(追記)全16時間の統計学動画講座を公開しました!☆4.8の超高評価をいただいている講座です.こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください.
統計学講座も第29回まできました.
今回は検定における第1種の誤りと,第2種の誤りについて解説したいと思います.

統計学お得意の難しそうな用語ですが,言ってることは全然難しくないのでサクッとやっていきましょう!
この辺りの話がわかると,より詳細に「仮説検定で何がわかるのか」を理解できるようになり,正しく検定を使うことができるでしょう.
目次
第1種の誤りと第2種の誤りってなに?
前回の記事で,実際に比率の差の検定をしてみました.前回の検定では,帰無仮説が採択され「二つの母集団の比率の差に有意差はなかった」という結果になりました.
この検定自体が間違えているケースを考えてみましょう.仮説検定において事実とは異なる結果が出てしまう(つまり”誤り”)ことも当然あり得ますよね?
仮説検定が誤るケースは,以下の二通りです.これをそれぞれ第一種の誤り(type one error)と第2種の誤り(type two error)と呼びます.
第1種の誤り:帰無仮説が正しいのにも関わらず,検定の結果帰無仮説を棄却してしまう誤り
第2種の誤り:帰無仮説が正しくないにも関わらず,検定の結果帰無仮説を採択してしまう誤り

具体例で考えてみましょう.
前回の例同様「ある工場で生産する製品の不良品率を下げるために,生産過程に変更を加えます.変更前と変更後で不良品率が下がったかどうかを仮説検定する」ケースを考えてみましょう.
この場合,帰無仮説は「変更前と変更後で不良品率は変わらない」であり,これを棄却することをねらって仮説検定をしていくんでした.
不良品率が下がったことを確認したいので,対立仮説は「変更後の不良品率は変更前より低い」とし,片側検定をすればいいことになります.(この辺りが「?」な人は前回の記事をもう一度読みましょう!)
さて,前回は検定の結果帰無仮説を採択しました.つまり「変更前と変更後で不良品率が下がったとは言えない(つまり,不良品率に違いがあるとは言えない=有意差はなかった)」という結果だったわけです.
でも,もしかしたら本当は今回の生産過程の変更により不良品率が下がってるかもしれません.たまたま今回の標本だと,有意差がでなかっただけかもしれませんよね?
これが第2種の誤りです.本当は有意差があるのにないと判断されてしまうケースです.
そして,もう一つのケース,つまり本当は今回の生産過程の変更によって不良品率は変わらないのに,有意差が出てしまい帰無仮説を棄却してしまう誤りを第1種の誤り言います.
以下の様に表にするとわかりやすいです.
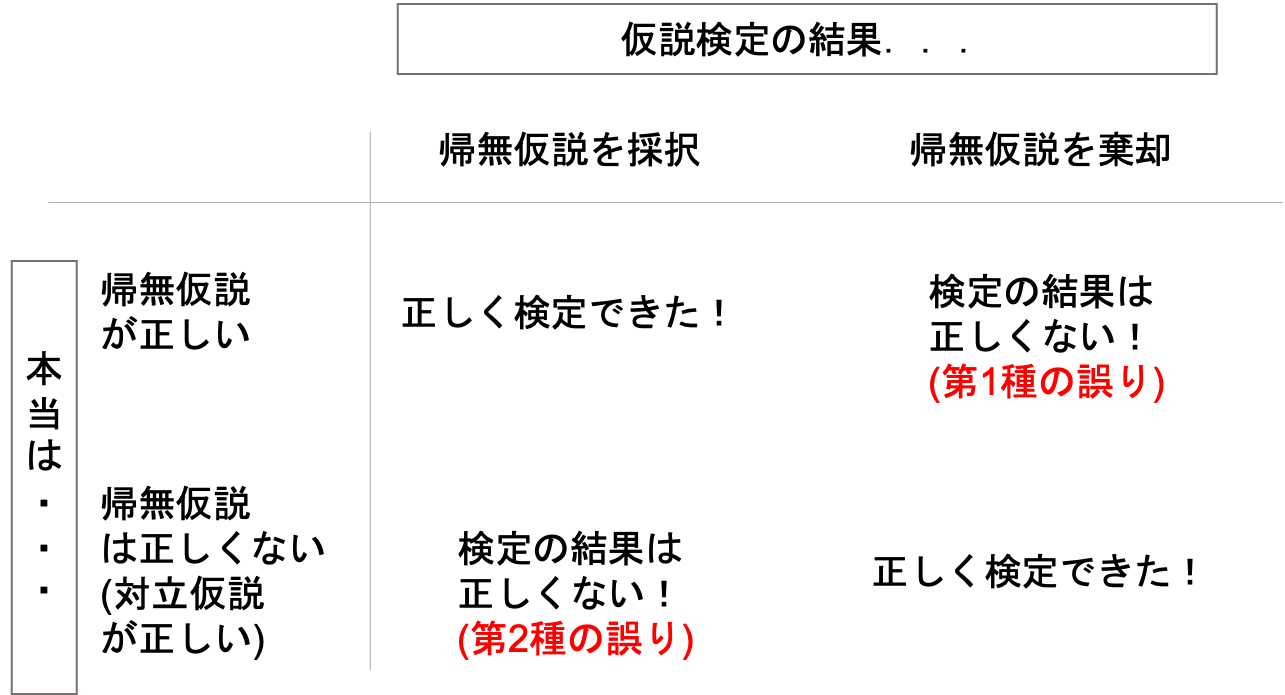

無理して覚える必要はないのですが,実は,簡単(!?)に覚える方法があります.
覚え方(どっちがどっち?)
第1種の誤りと第2種の誤りの覚え方を解説する前に,第1種の誤りの”確率”について説明します.
検定をする上で,これらの誤りがどれくらいの確率で起こるのかを知ることは重要ですよね?
まず,第1種の誤り(つまり,本当は帰無仮説は正しいのに誤って棄却してしまう)が起こる確率はどれくらいでしょうか?
「帰無仮説は正しい」という状況は固定して考えてください.「帰無仮説が正しいのかどうか」というのは確率的に変動するものではありません.
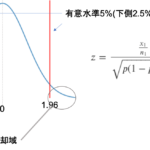
帰無仮説を棄却してしまう確率というのは,有意水準と等しいことがわかると思います.例えば有意水準を5%に設定すると,標本から得られた推定量が5%未満の確率で得られる様な稀な値であれば帰無仮説を棄却するわけですから,そのまま有意水準の値が帰無仮説を棄却してしまう確率であることがわかると思います.
有意水準を\(\alpha\)で表すことは第27回で紹介した通りです.そして,第1種の誤りの確率も\(\alpha\)で表します.(有意水準=第1種の誤りの確率ですからね!)
そしてこれは,「あ(a)わてて棄却する\(\alpha\)」と覚えましょう.
仮説検定は,帰無仮説を棄却することを最初から“狙って”行うものです.つまり,検定をする際には「帰無仮説を棄却したい,棄却できるだろう」と思いながらやるわけです.
なので,実際には帰無仮説が正しいのに“あわてて”有意差があると判断して帰無仮説を棄却してしまうのが第1種の誤り(=\(\alpha\))だとイメージできると思います.
そして,第2種の誤りを\(\beta\)と言います.第1種が\(\alpha\), 第2種が\(\beta\)なので,順番通りでわかりやすいですね.
\(\alpha\)と\(\beta\)はトレードオフ

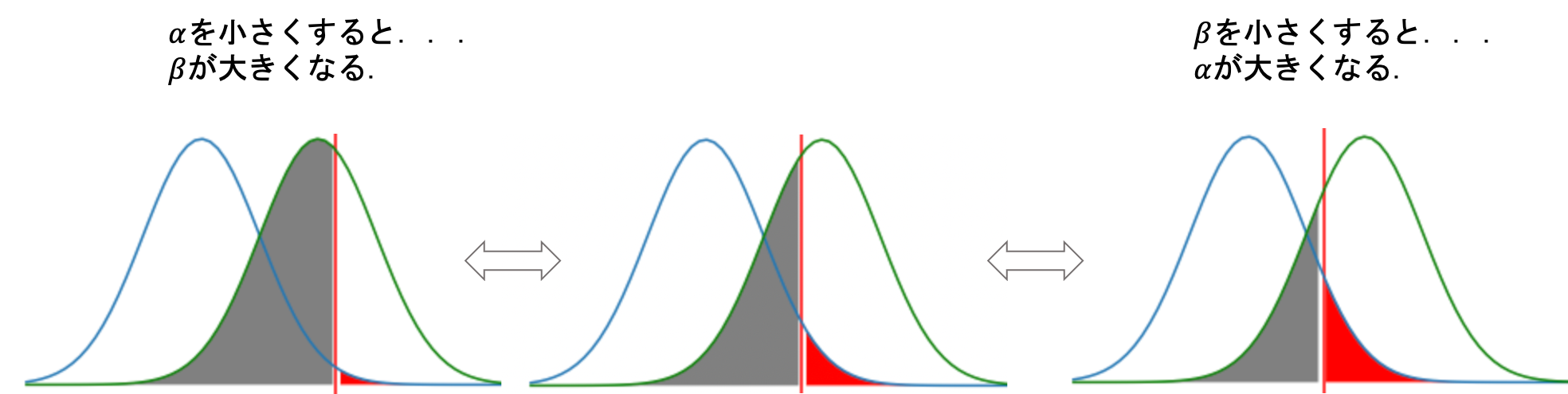
その通り.その通りなんですが,実は\(\alpha\)を小さくしようとすると\(\beta\)が大きくなり,\(\beta\)を小さくしようとすると,やはり\(\alpha\)が大きくなってしまい,\(\alpha\)と\(\beta\)を同時に小さくすることはできないんです.
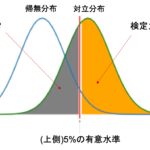
これを視覚的に理解するために,帰無仮説が正しい場合の検定統計量(例えば前回の比率の差の検定でいう\(z\))の分布(=帰無分布)と対立仮説が正しい場合の検定統計量の分布(=対立分布)を使って説明します.
まずは帰無分布について見てみましょう
通常帰無仮説が正しいという仮定で検定統計量を計算し,その分布で有意水準未満であれば帰無仮説を棄却していたので,帰無分布というのはまさに通常の検定の手順で確認する検定統計量の分布ですね.
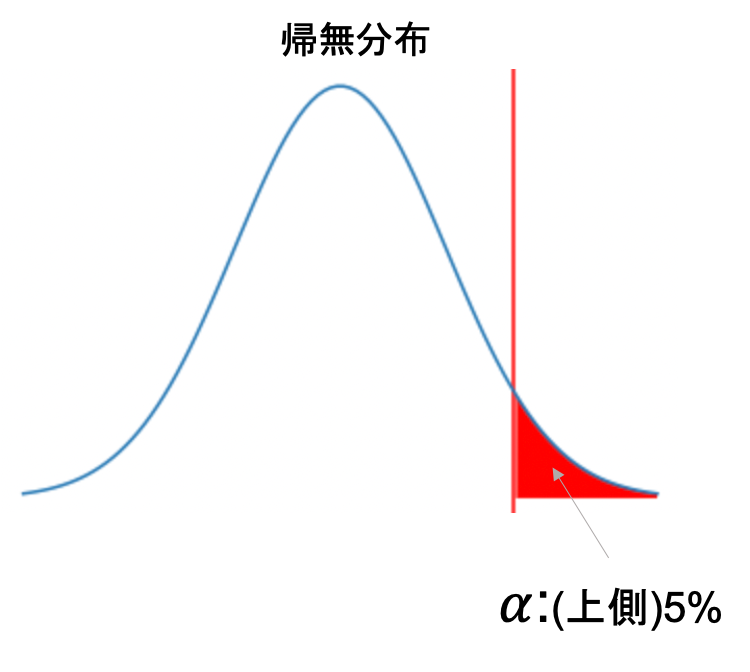
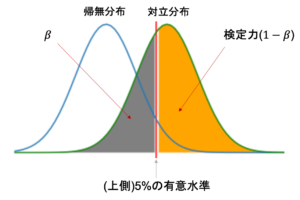
前回の比率の差の検定の際も,帰無分布をみて例えば上側5%の有意水準を棄却域に設定していたんでした.この有意水準がそのまま第1種の誤りの確率になります.(上図は片側検定で有意水準上側5%の例)
ここに,対立分布を描画してみます.対立分布は対立仮説が正しい場合の統計検定量の分布です.対立分布は「差がある」ことを想定しているので,帰無分布よりすこし差がある(ずらした)分布になるはずです.(↓こんな感じ)
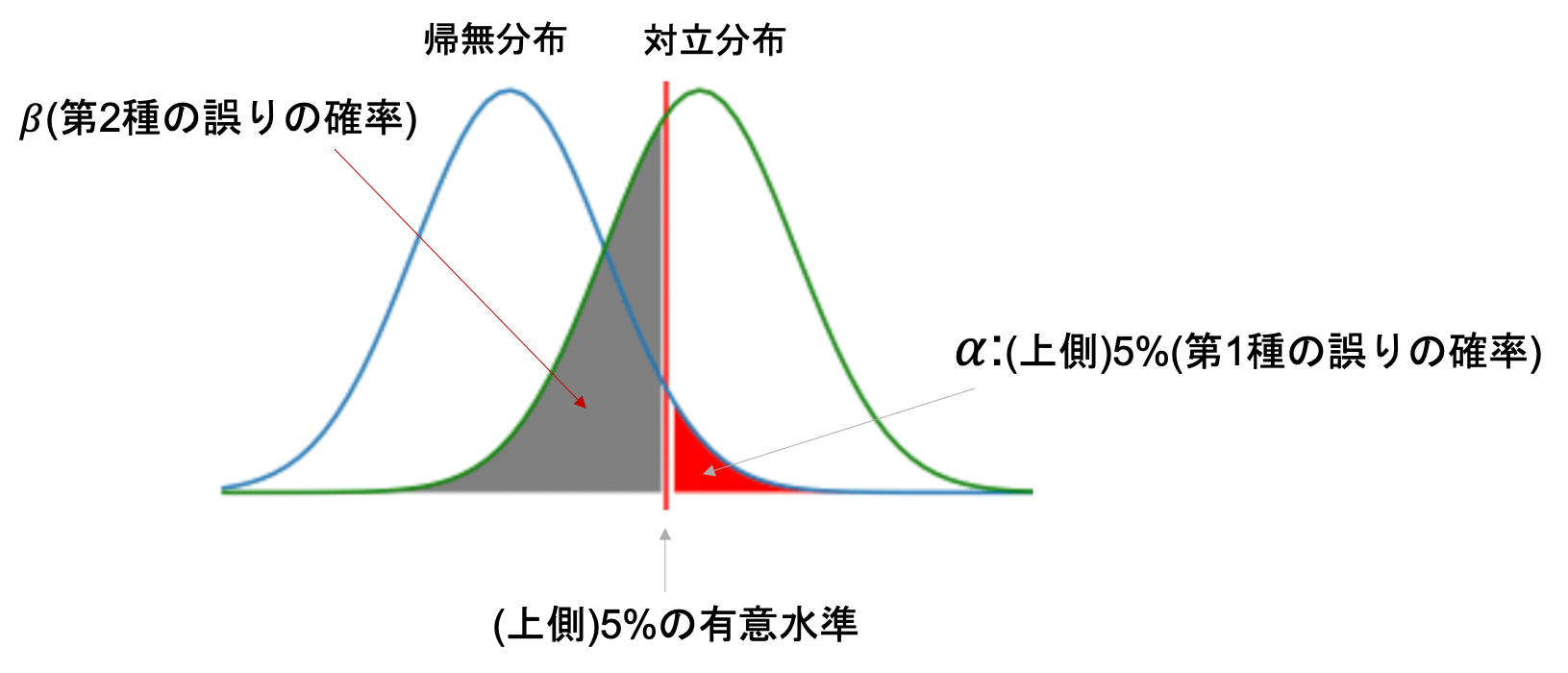
上の図の灰色の部分が第2種の誤りの確率になります.つまり,本当は対立仮説が正しいのに帰無仮説の棄却域(上図の赤の部分)に入らなかったので帰無仮説を採択してしまう確率ですね.
この図をみると,\(\alpha\)を小さくしようとすると\(\beta\)が大きくなり,\(\alpha\)を大きくすると\(\beta\)が小さくなるのは簡単にイメージできると思います.

ここでは,もう一つ別の指標「どれだけ正しく帰無仮説を棄却し,対立仮説を成立できるか」について考えてみましょう.
つまり,対立仮説が正しい状態で,どれだけきちんと帰無仮説を棄却できるのかということです.検定をする際には常に帰無仮説を棄却することを狙っているわけですから,「どれだけ正しく帰無仮説を棄却し,対立仮説を成立できるか」というのが検定をする上で鍵になるはずです.
この指標のことを検定力(power)と言います.検出力と言ったりもします.
検定力を理解することは検定を行う上で重要になってきます.非常に重要な指標だと言えるので,次回の記事で詳しく解説していこうと思います!
まとめ
今回は仮説検定における第1種の誤りと第2種の誤りについて解説をしました.
- 第1種の誤り:帰無仮説が正しいのにも関わらず,検定の結果帰無仮説を棄却してしまう誤り
- 第2種の誤り:帰無仮説が正しくないにも関わらず,検定の結果帰無仮説を採択してしまう誤り
- 第1種の誤りの確率は有意水準に等しく,同様に\(\alpha\)という
- 第2種の誤りの確率を\(\beta\)という
- 「あ(a)わてて棄却する\(\alpha\)」と覚えるといい
- \(\alpha\)と\(\beta\)はトレードオフの関係にあり,同時に下げることはできない
今回の記事は,検定力への導入の意味合いもあります.
次回の記事で検定力について解説をしていきます.非常に重要な指標なのでしっかり押させておきましょう!
それでは!
追記)次回の記事を書きました