ついにこの統計学講座も第30回まできました.ここまで読んでいる人(どれくらいいるかな笑)は,かなり統計リテラシーがついているかと思います.
今回は前回の記事の続きで,検定力(power)について詳しく解説していきます!
(追記)全16時間の統計学動画講座を公開しました!☆4.8の超高評価をいただいている講座です.こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください.
目次
検定力とは?
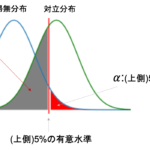
第1種の誤り(\(\alpha\))と第2種の誤り(\(\beta\))がトレードオフの関係にあって,同時に下げることができないことを前回の記事で解説しました.(以下再掲)(青線が帰無分布,緑線が対立分布です)
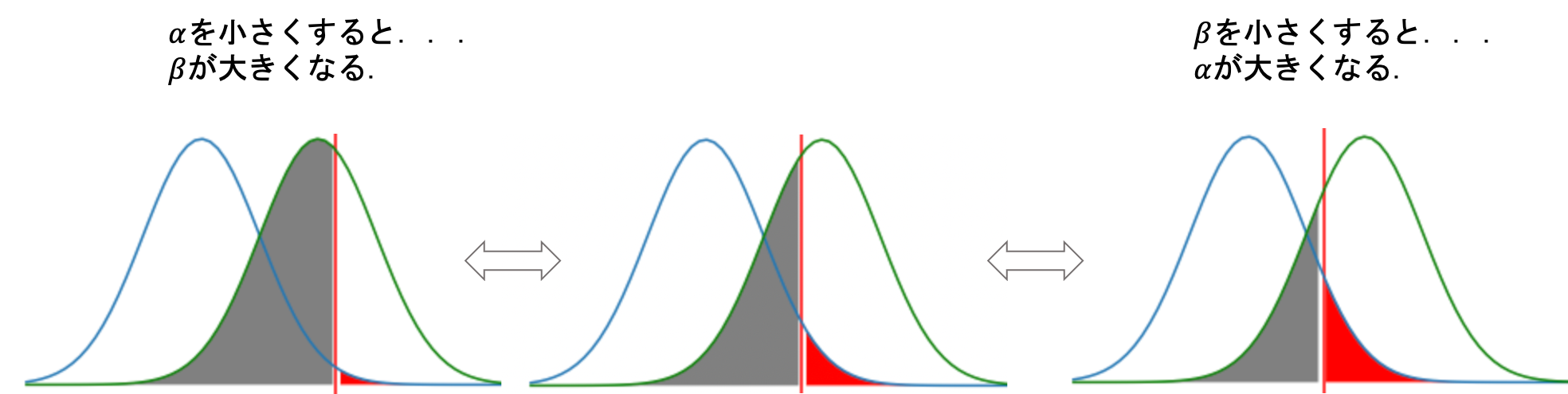
今回の記事では,もう一つ別の指標「どれだけ正しく帰無仮説を棄却し,対立仮説を成立できるか」について考えてみましょう.
仮説検定は,「帰無仮説を棄却して対立仮説を成立することを狙っている」ので,それをどれだけ正しくできるのかというのが鍵になるのはわかると思います.
この指標のことを検定力(power)と言います.(検出力と言ったりもします)
検定力は,対立仮説が正しい場合に帰無仮説を棄却する確率なので,帰無分布と対立分布の図でいうと以下のオレンジ色の部分になります.つまり,\(1-\beta\)になることがわかると思います.
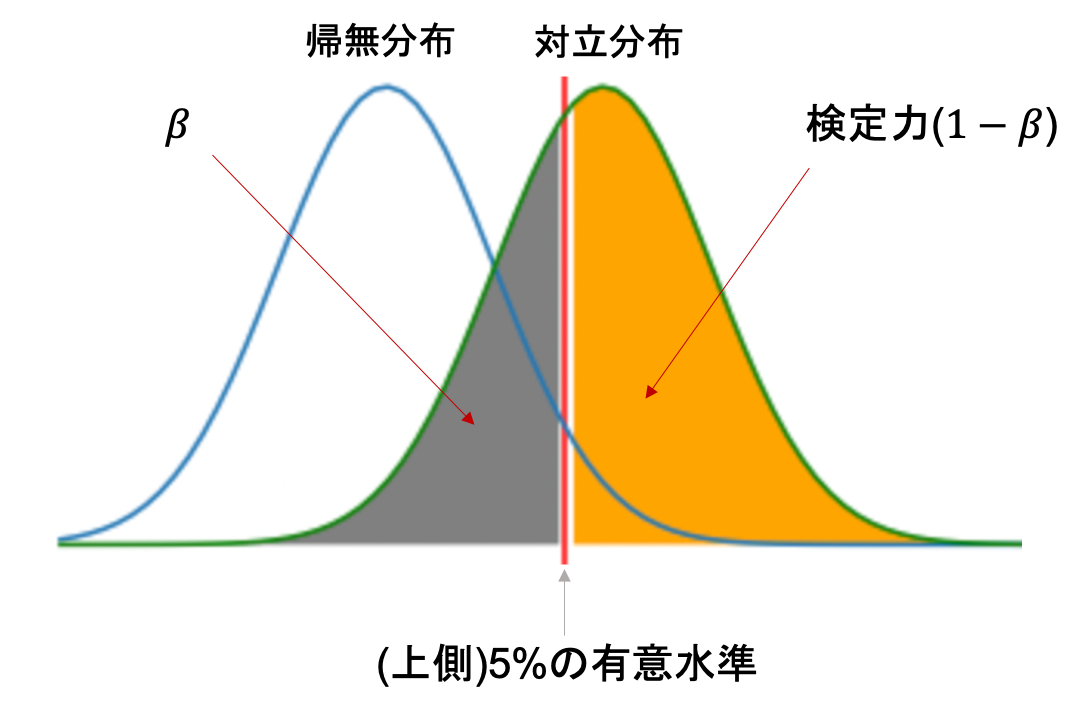
表でいうと以下の部分です.
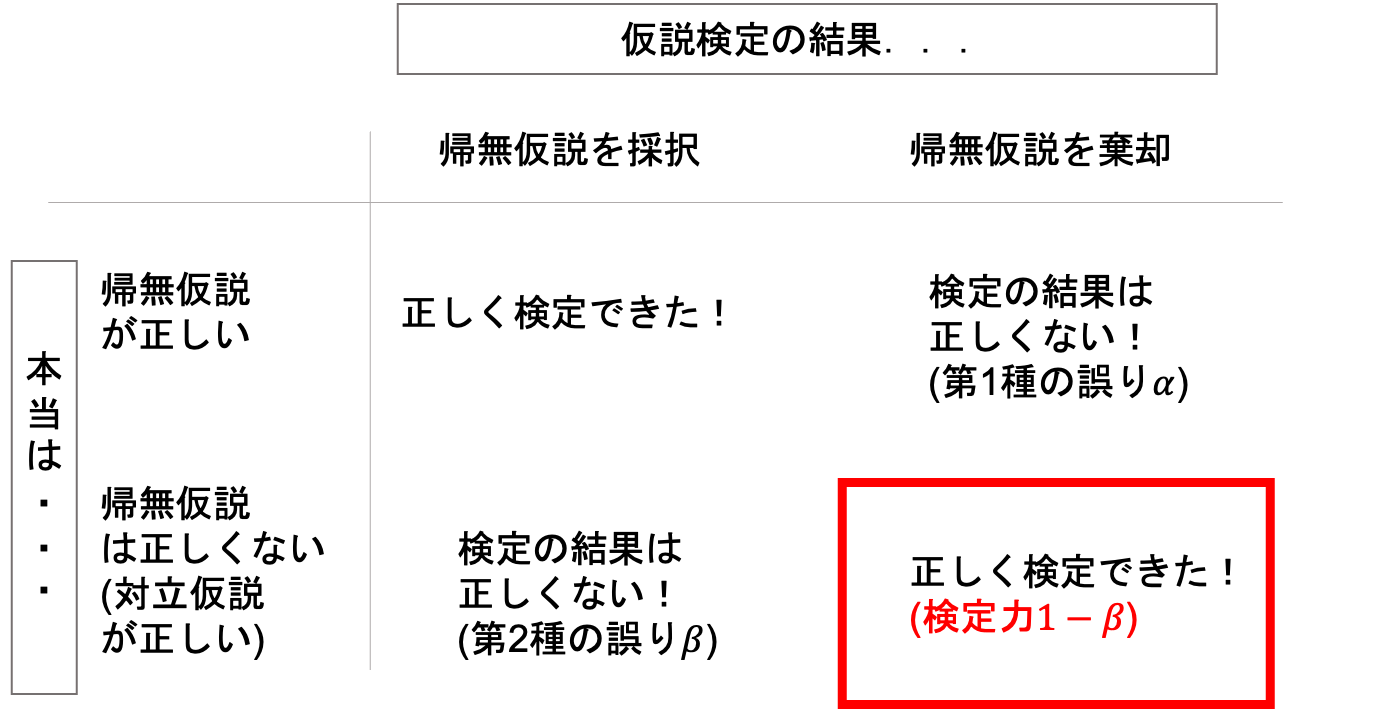
検定する際には帰無仮説を棄却することを狙っているので,この検定力が高い方が都合がよくなるわけです.(しかし,高すぎるのも問題です.この辺りも含め,今回の記事で解説していきます.)
では,この検定力が高いというのは,どういう時なのか?大きく三つあります.
1.有意水準が高い
2.サンプルサイズ(標本の大きさ)が大きい
3.帰無分布と対立仮説が離れている
それぞれみていきましょう!
検定力を高くするには?高すぎるといけない理由
まず第一に,有意水準を高く設定すると検定力も高くなります.図で見ると一発ですね.有意水準を高くするということは,それだけ帰無仮説を棄却する確率が上がるわけですから,対立仮説が成立する確率が上がります.(青線が帰無分布,緑線が対立分布です)
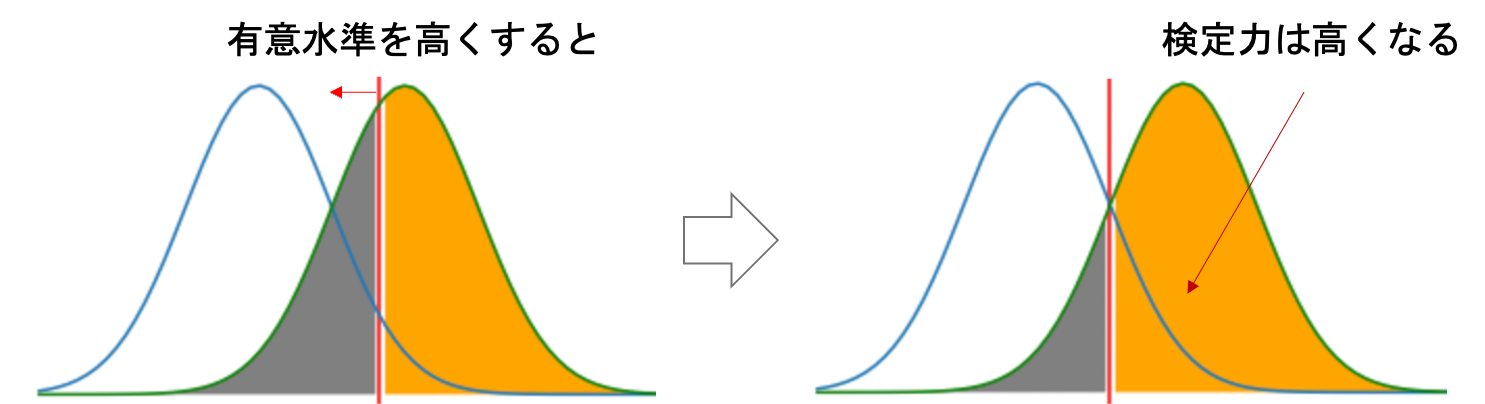
しかし,有意水準を高くすると出来レース的な結果になってしまうので,普通有意水準を意図的に高い数字を設定することはありません.
一般的に有意水準には5%か1%を使うので,それよりも高い水準を使うというのはそれだけ帰無仮説を意図的に棄却しやすくしているとされ,受け入れられるものではありません.
なので,有意水準\(\alpha\)を固定したうえで,どのように検定力を高められるかを考えてみましょう.
次に,サンプルサイズとの関係を見てみます.
サンプルサイズを大きくすると,帰無仮説を棄却できる可能性が高くなるのはイメージできると思います.
例えば前々回の例で,変更前後の不良品率が,標本100個のうちそれぞれ4%と5%であるのと,標本を1万個とって不良品率がそれぞれ4%と5%とでは信頼度が違いますよね?
これは図で見ても明らかです.サンプルサイズが大きくなるということは,標本分布の分散が小さくなるということです.つまり,帰無分布や対立分布が細く尖るイメージですね!なぜ分散が小さくなるかは第7回を参照してください.
つまりこういうこと↓(青線が帰無分布,緑線が対立分布です)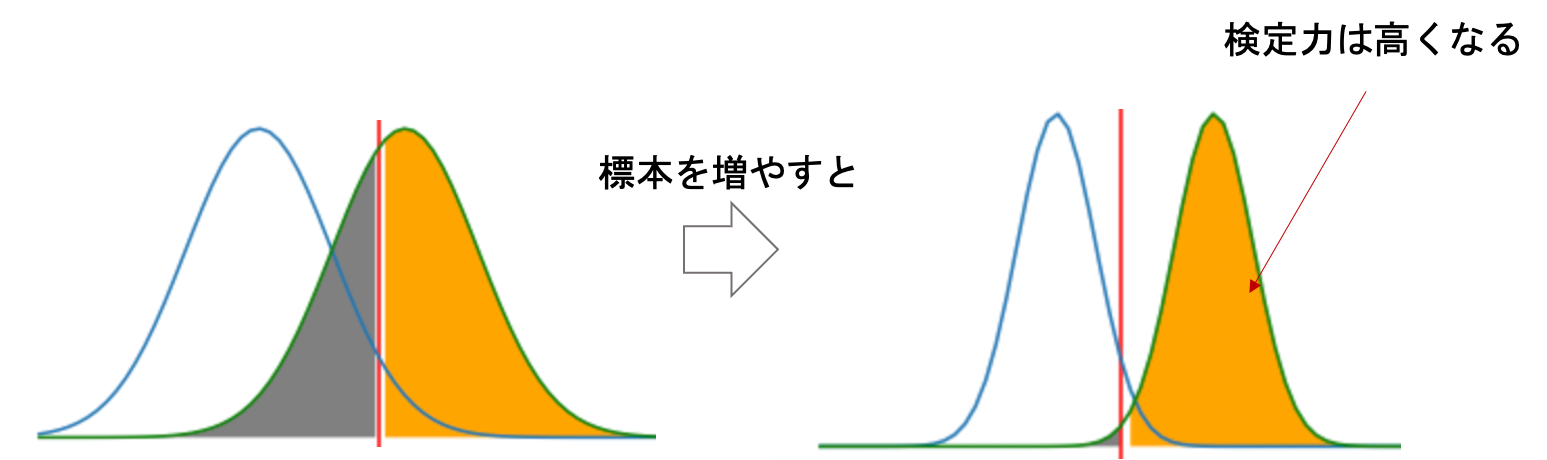
この時,有意水準は変わっていないところに留意してください.(今回の図では上側5%)

と思う人が多いんですが,これには注意が必要です.
検定力が高すぎると,微妙な差でも有意差ありと判断されてしまうからです.(青線が帰無分布,緑線が対立分布です)
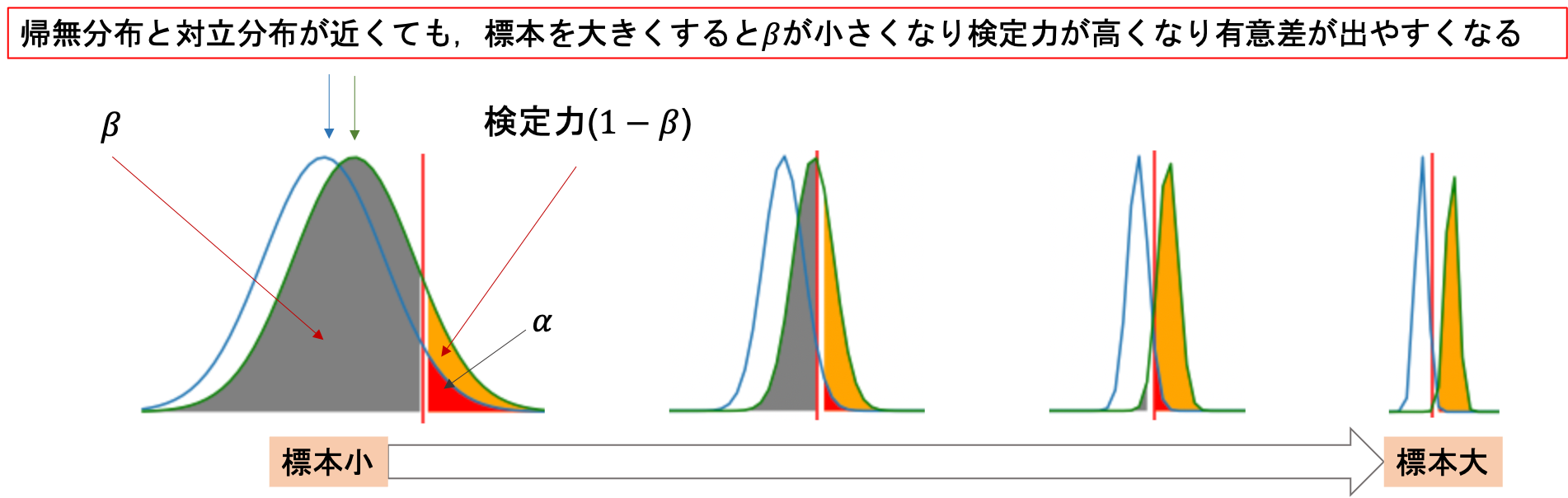

まぁ確かにこれだけだと実際にある微妙な差を検出できて良いように聞こえるんですが,実際の検定の際に大標本で検定をして,微妙な差を検知して「有意差あり」と言われてもしっくりこないですよね?それってサンプルサイズが大きすぎるから,微妙な差を拾ってませんか?ってなるわけです.
最近はビッグデータでの解析が当たり前になってきたので,かなりの大標本で検定をすることが可能になってきています.例えば数万件の標本同士の平均をみて,「ほらね,有意差ありでしょ?」と言われても,もはやそれは検定の意味を成していない場合があります.数万件も標本があれば,微妙な差でも「有意差あり」と判断されてしまうからです.
さらに言うと,それだけの標本からデータを得られたのなら,母集団の差の検定をせずとも今あるデータを使って有意義な分析ができそうです.もはやそんな標本に対して差の検定をするまでもなく,実際のデータの分布と値を見れば良いケースがほとんどです.「何でもかんでも検定をしてp値を出す」というのはナンセンスです.
「サンプルサイズを大きくすると,本当は差がないのに有意差がでてしまう」というのは間違えです.「本当は差がないのに有意差がでてしまう確率」は\(\alpha\)であり,これは標本の大きさに寄りません.ただ現実問題,本当に差があるのかわからない状況で検定を行う上に,本当に差がない母集団同士を検定することは滅多にないです.多かれ少なかれ,少しは差があるケースがほとんどです.(前々回の例でも,工場の生産過程を変えたなら不良品率は全く一緒にはならないよね?という期待があります.).つまり,検定をする際には暗黙的にある程度差があるだろうけど,それって有意なの?というのを確かめたいわけです.(本来「程度差」を検定するものではないのでおかしな話ですが).そこでサンプルサイズが大きいと,小さな差があったとしても有意差と出てしまうので「検定の結果があまり参考にならなくなってしまう」恐れがあるわけです.これが検定力が高すぎるといけない理由です.

多くの参考書では,Cohenが提唱した0.8という数字が適切な検定力だとしています.なので,0.8になる様にサンプルサイズを調整するのが一般的です.
しかし,検定力を決める要因としてもう一つ「二つの母集団の差がどれくらいあるのか」という指標があります.つまり「帰無分布と対立分布がどれくらい離れているか」ということです.この指標のことを効果量(effect size)と呼びます.(検出したい差(効果)の量ということですね)
厳密には効果量は「標準化された平均値差」です. 帰無分布や対立分布は,通常標準化された検定統計量の分布であり,実際の母集団の分布を表しているわけではないので注意です.
帰無分布と対立分布が離れていれば当然検定力があがるのはイメージできると思います.明らかに差がある母集団を検定するのは,差が微小な母集団を検定するよりも簡単に帰無仮説を棄却できますからね.(青線が帰無分布,緑線が対立分布です)
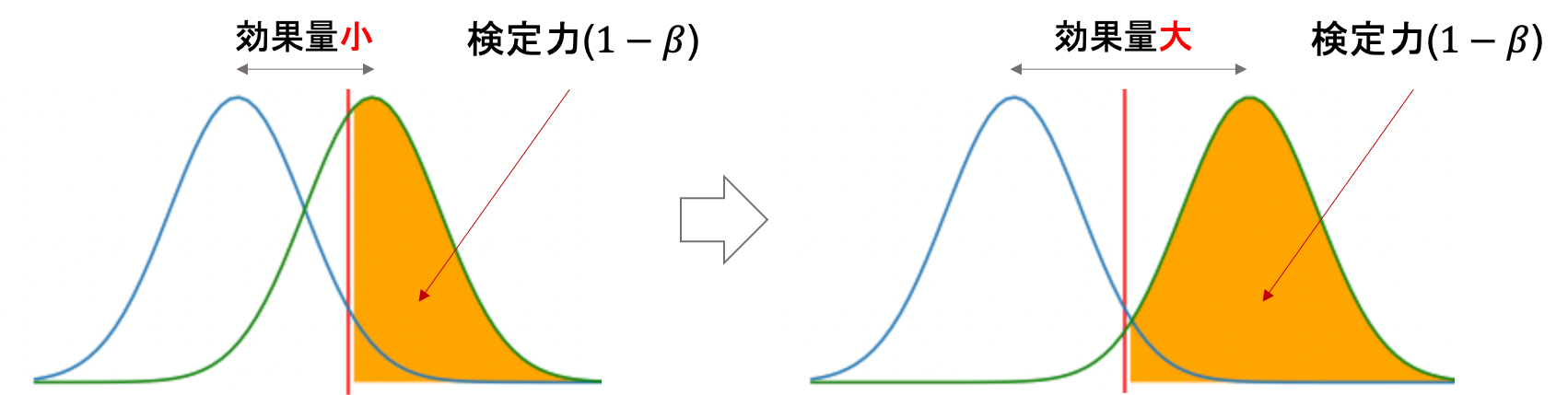

そうなんです.そもそも母集団に差があるといえるかを検定しているのに,母集団の差がどれくらいあるかなんて当然わかりませんし,検定力を上げるために操作できるものでもありません.
じゃぁどうするのか?通常,過去のデータや経験から定めます.効果量の求め方や決め方については,また詳しく記事を書いていこうと思います.
つまり,p値だけでは検定の結果報告としては不十分で,有意水準と効果量と検定力とサンプルサイズをそれぞれ提示して初めてその検定の意義があります.普通は有意水準は固定でサンプルサイズは表記しますが,それに加えて効果量と検定力についても明記させる論文も多いです.
つまり,検定力を決める要因として有意水準,サンプルサイズ,効果量があるわけですね.
そして検定力は0.8を目指し,有意水準は通常5%(もしくは1%)とし,効果量は過去のデータ等から計算して求めるので,検定時に設定できるものはサンプルサイズのみです.
つまり,有意水準5%であらかじめ得られた効果量を元に,検定力が0.8になるように標本の大きさを決める必要があるということです.
では,実際にどのように標本の大きさを決めていくのか?これを行う分析のことを検定力分析(power analysis)と呼びます.これについては,また別の記事で解説をしていこうと思います.
今回はひとまず,検定力について押さえておきましょう!
まとめ
今回は検定を行う上で鍵となる検定力について解説をしました.
- 検定力とは「正しく帰無仮説を棄却し,対立仮説を成立できる確率」のことで第2種の誤りを\(\beta\)とすると,\(1-\beta\)で表される
- 検定しようとしている標準化された2つの母集団の差を効果量と呼ぶ
- 検定力を決める要因として,有意水準,サンプルサイズ,効果量がある
- 検定力は高ければいいわけではなく,通常0.8を確保することが推奨されている
- 効果量は,過去のデータや経験から仮定した値を使う
- 有意水準を固定し効果量を決めた後に,検定力がある値(主には0.8)を確保できるようにサンプルサイズを決めていく(検定力分析)
サンプルサイズの決め方や検定力分析の詳しい内容については,また別の記事に書いていく予定です.
検定力と効果量については今後の検定でも時折触れていきますので,今回の記事はその導入ということで!
次回以降は他の検定(連関の検定や平均値差の検定,分散の検定等)について触れていきます.
それでは!
追記)次回の記事を書きました!