Pythonで学ぶデータサイエンス入門:統計編第18回です.
(追記)全16時間の統計学動画講座を公開しました!☆4.8の超高評価をいただいている講座です.こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください.
前回までの記事では統計学の”記述統計”という分野に焦点を当ててきました.
統計学で使う様々な指標をみてきたわけですが,今回の記事からは統計学のもう一つの分野である”推測統計”を扱っていこうと思います.
この推測統計がわかるようになると,手元にあるデータ(標本)を使ってそのデータの裏にある,そのデータを生み出したデータ(つまり母集団)の特性を(統計的に)知ることができます.これは現代において多くの人が統計学を学習する理由でもあります.
例えばある製品の耐久性を調べるのに落下実験を行うとします.当然製造した全ての製品に対して落下実験を行うことはできないので,例えば100個だけランダムにとってきて,その100個に対して実験をして製品の耐久性を推測する必要があります.
他にも,自社製品のユーザ満足度を測るのに全員のユーザからフィードバックをもらうことは不可能なので,一部のユーザからのフィードバックをもらい,それに基づいてユーザ全体の満足度を推測する必要があります.
これらを例えば異なる手法間(異なる工場で生産した製品の耐久性や,アップデート前後の自社サービスのユーザ満足度など)で比較したいときがあると思います.
こういうときには母集団から一部の標本を取ってきて,その標本を調べることで母集団の特性を推測することが有効なわけです.
というわけで,今回の記事から統計学の真髄とも言える”推測統計”に入っていくわけですが,推測統計を学ぶ上で欠かせないのが“確率”の考え方です.
だって母集団から取ってきた標本は確率的に変動するからね!運が悪ければ母集団とは似ても似つかない標本を取ってきてしまうわけです.
先の例でいうと,「落下実験を行った100個全部がたまたま不良品だった」なんて可能性も0ではないわけです.
今回は統計学を学ぶ上で欠かせない”確率変数”と”確率分布”を解説していきます.多分,統計学を勉強した人でもイマイチ理解できてない人多いんじゃないかなぁと思うので,超わかりやすく理解できるように解説するので付いてきてください!
確率変数や確率分布という単語は,今後の統計学講座でも多用します.今回の記事で押さえておきましょう!
目次
確率変数とは?
こちらの記事でも少し紹介しましたが,改めて確率変数(random variable)について解説をします.
確率変数って,名前がごつくてとっつきにくそうなんですが,何も難しいものじゃありません.
確率変数は「値が確率的に変動するような変数」だと思えばOKです.
例えば「サイコロを振ったときに出る目」は確率変数です.サイコロを振って出る目は「1~6」の値で,それぞれ出る確率は1/6です.
このようにとりうる値にそれぞれ確率が対応しています.少し難しく思えるかもしれませんが,確率的に変動する事象について考えるときに確率変数の概念があると議論がしやすくなるので便利なのです.
そして統計学を学ぶ上で重要なのは,標本統計量も確率変数だということです.

標本統計量は,母集団の特性を推測するのに使用する標本の特性値です.例えば平均とか分散とか標準偏差とかです.今ままでの講座の内容で扱ってきた指標ですね.
母集団からランダムに標本を取ってきたとき,標本統計量の値って当然確率的に変わりますよね?
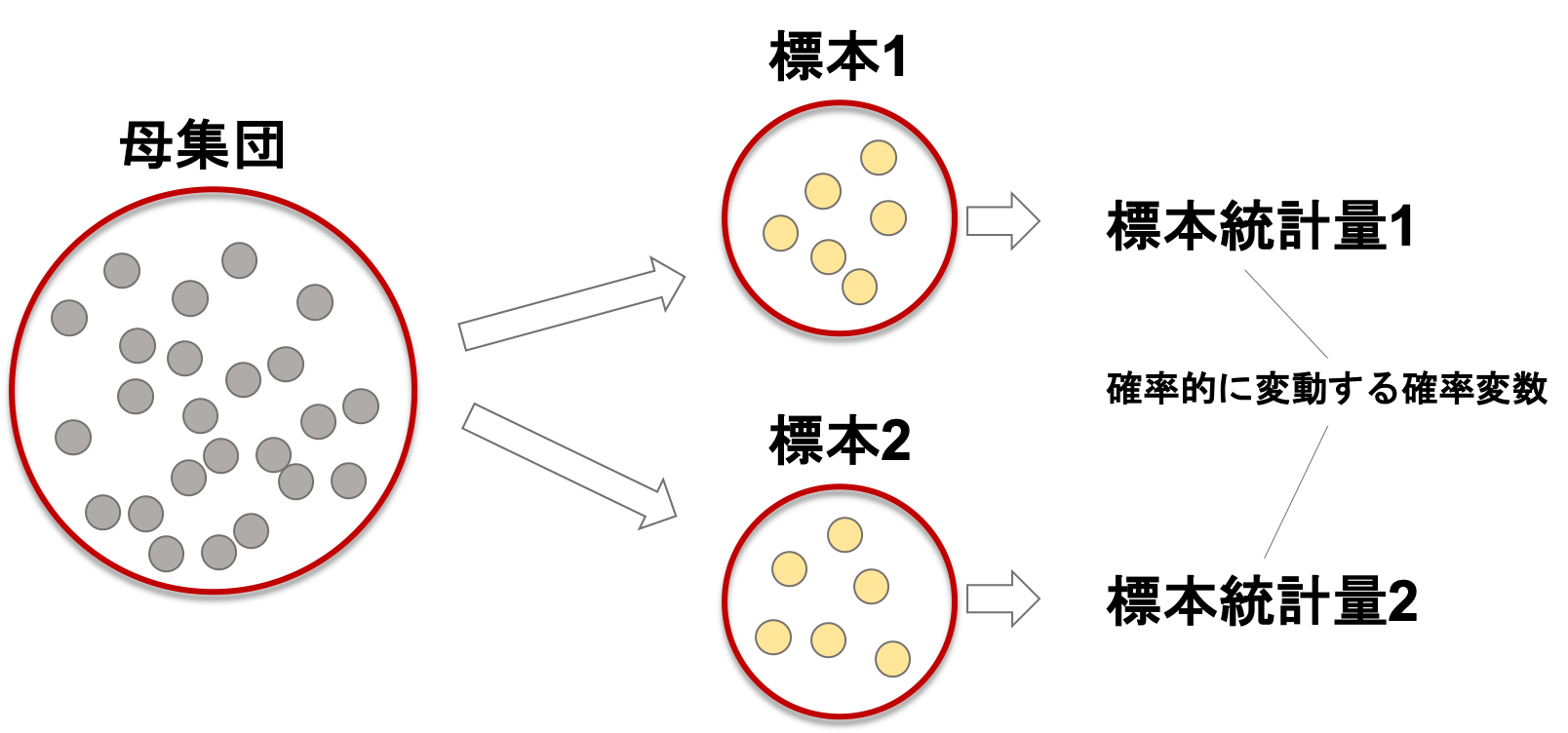
例えば日本の成人男性が母集団で,そこから仮にランダムに何名かの成人男性を標本をとして2回取ってきたとしましょう.
仮に全国の成人男性の平均身長が172cmだとします.この2つの標本の身長平均(標本平均)は,当然172cmにぴったり一致するわけはありません.それぞれの標本の標本平均も異なるでしょう.
しかし,標本平均が母平均の172cmから大きく外れる可能性は低く,例えば160cmとか180cmになる可能性よりも170cm前後になる可能性の方が高いです.
つまり,標本平均は確率的に変動するといえます.
標本統計量は確率的に変動する確率変数だという考え方は非常に重要なので押さえておきましょう!!
確率分布とは?
確率分布(probability distribution)は,簡単にいうと確率変数の値とそれに対応する確率を表した分布です.
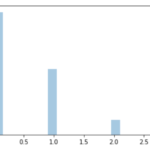
どういうことかというと,先ほどのサイコロの例を取ってみます.
サイコロのでる目は1~6で,それぞれ1/6の確率で出るので以下のように分布を書くことができます.
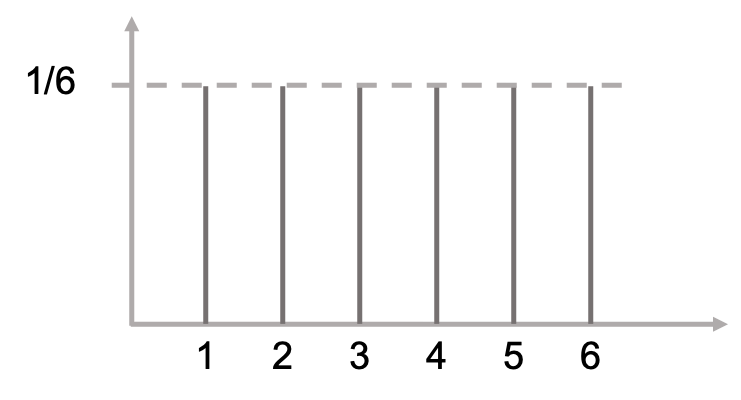
何も難しい話ではないですね.(ちなみに,このように各値に一定の確率が分布している確率分布を一様分布(uniform distribution)と呼ぶので覚えておきましょう.)
さて,サイコロの目のように飛び飛びの値,つまり離散的な値の場合,確率変数を離散型確率変数といいます.一方,連続的な値をとる場合の確率変数を連続型確率変数といい,その場合の確率分布は例えば以下のような曲線を描きます.
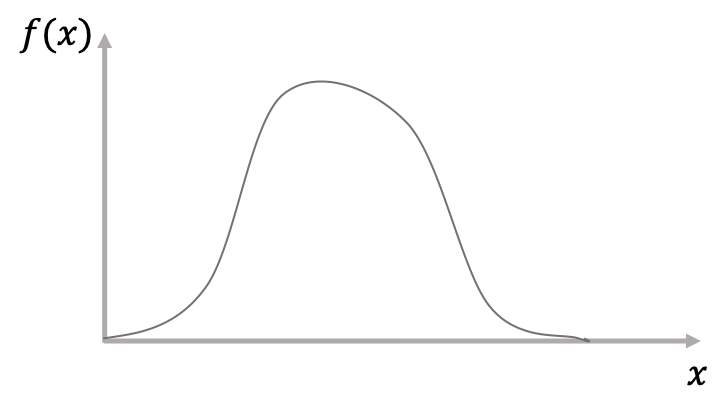
これは,確率変数\(x\)に対応する確率の分布を表しているものですが,これは,確率変数\(x\)に対してある関数を描画しているとも言えます.
この関数のことを確率密度関数(probability density function)といい,よく確率密度と呼びます.
非常に重要な単語なので覚えて欲しいのですが,確率密度関数については後ほど説明をします.
さて,先ほどの例で出した日本の成人男性の身長の標本平均をみてみましょう.「標本統計量は確率変数」ということは,「標本統計量はある確率分布に従っている」と言えますよね?
標本統計量が従う確率分布を,その統計量の標本分布(sampling distribution)と言います.これ,超超重要なのでしっかり押さえておきましょう.
これは,取ってきた複数の標本から計算した複数の標本統計量の分布ではないことに注意してください.
例えば,先ほどの例で日本の成人男性(平均身長172cm)からいくつか標本を取ってきて,それぞれの標本で平均身長を計算したとしましょう.例えば5つ標本を作って計算したら,手元にあるのは5つの標本平均です.
この標本平均が仮に168cm, 170cm, 171cm, 172cm, 175cmだったとします.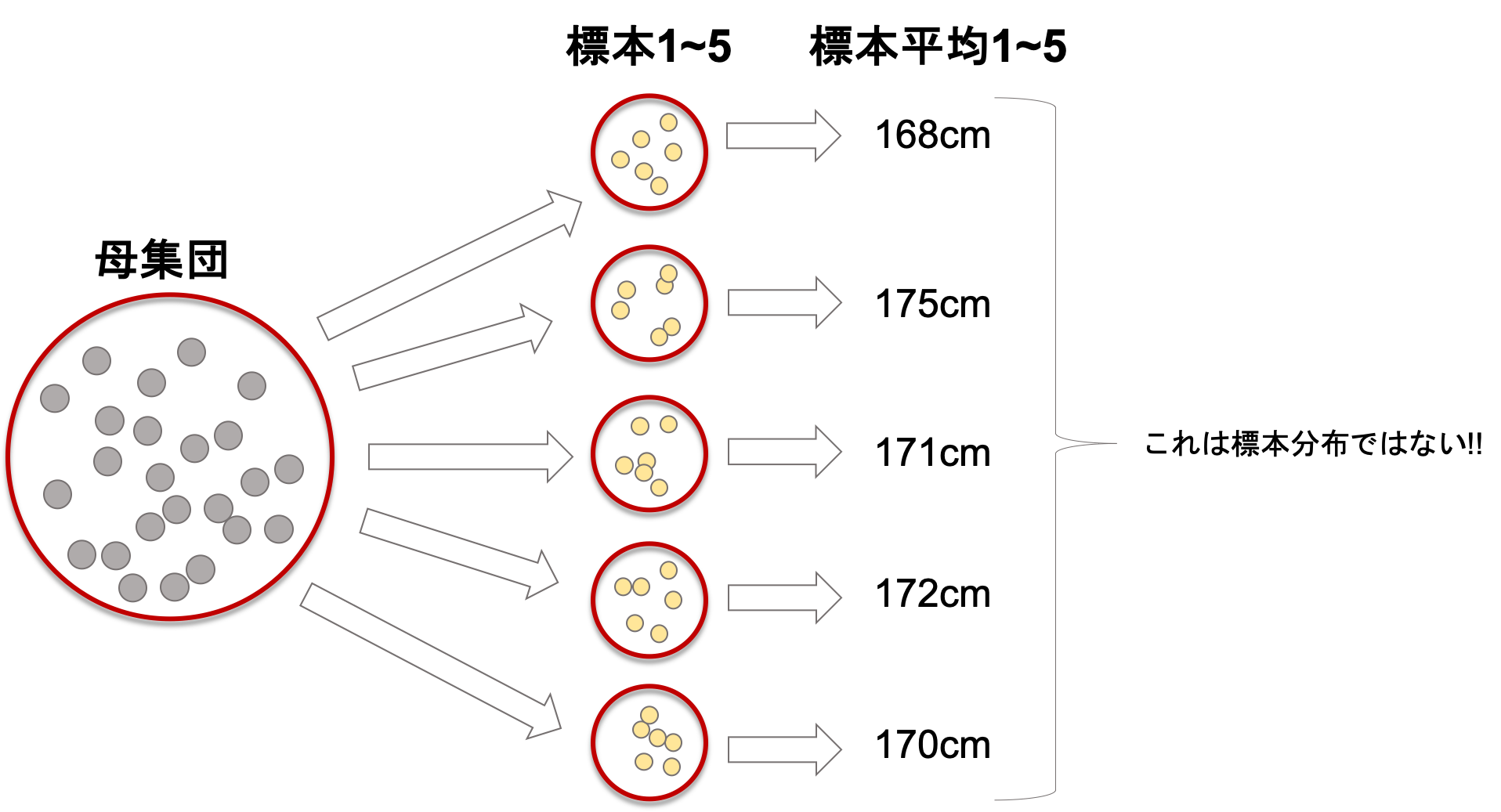
これらの値を「標本分布」と呼ぶわけではないです.
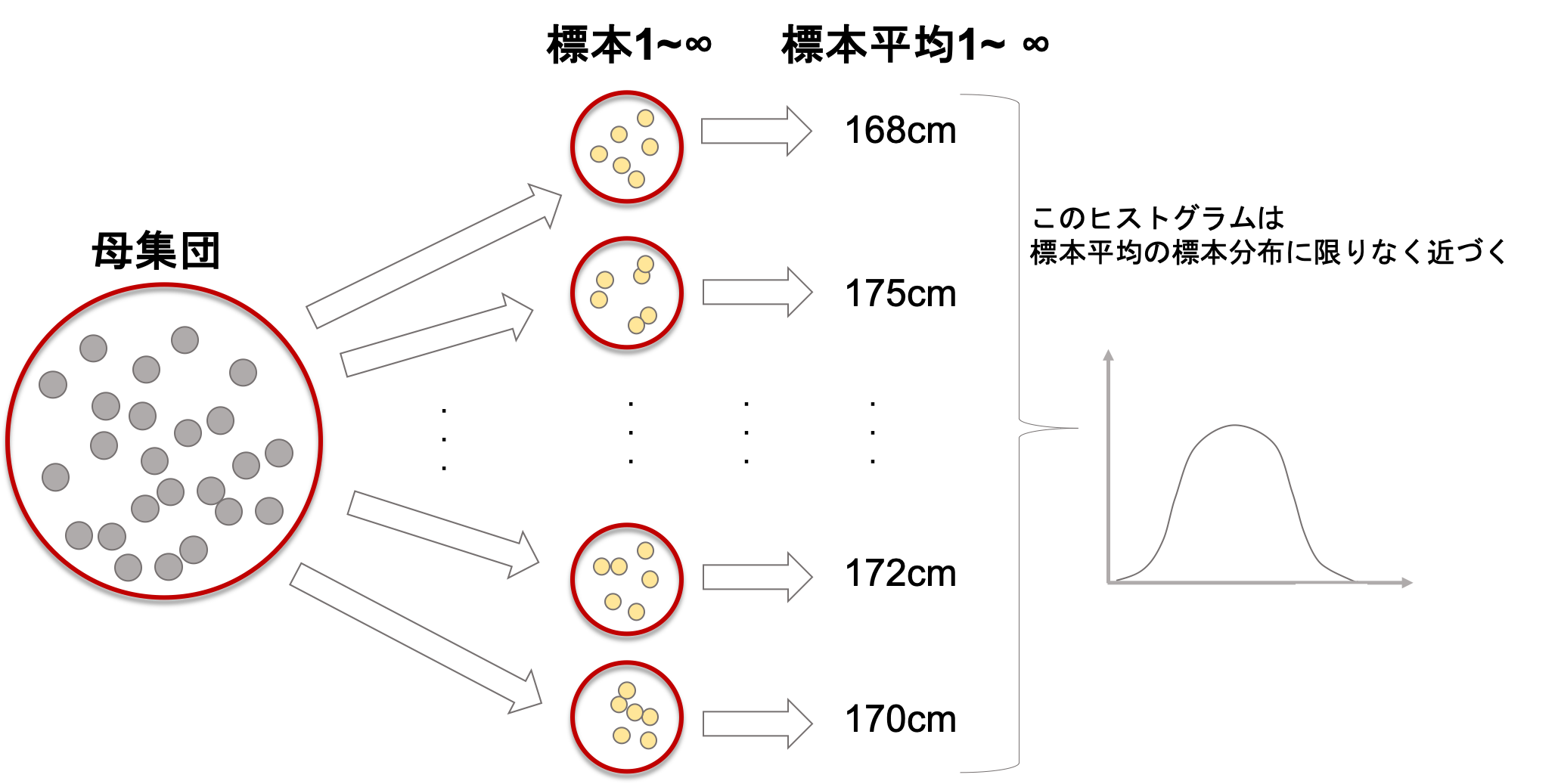
標本分布というのは,標本統計量(今回なら標本平均)が従う確率分布であって,目に見えるものではありません.
もし仮に標本を無限回取ってきて,無限個の標本統計量の(厳密には”正規化した”)ヒストグラムを取った場合は限りなくその統計量の標本分布に近くなります.
この辺りは結構誤解しやすいところなので押さえておきましょう!
確率密度関数から確率を計算する
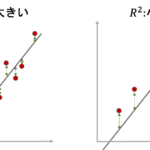
連続確率変数の確率分布において,確率変数がある区間の値をとる確率は,確率分布が表す曲線の面積になります.
図でいうとこんな感じ↓
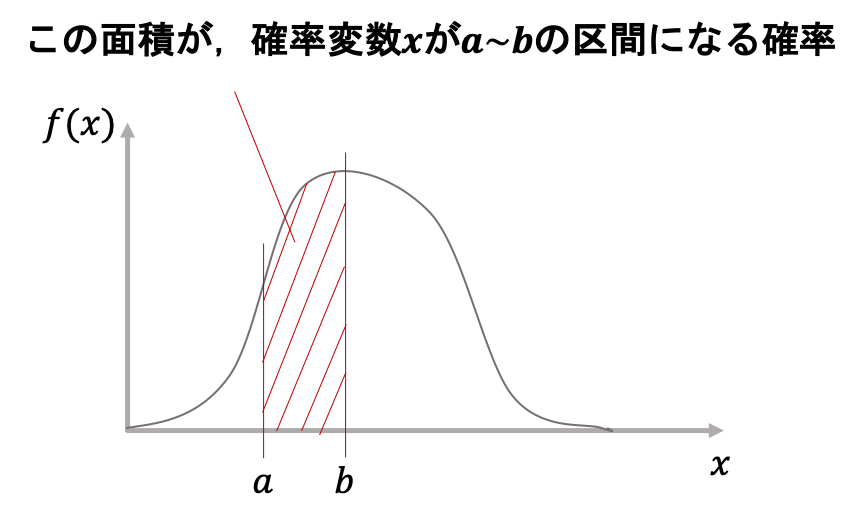
高校数学を覚えている人は,確率密度関数\(f(x)\)を\(a\)から\(b\)の区間で積分した値が上図の赤い斜線で表された面積になるというのがわかると思います.
これは逆に,確率変数\(x\)がある一つの値になる確率が0だということを意味しています.
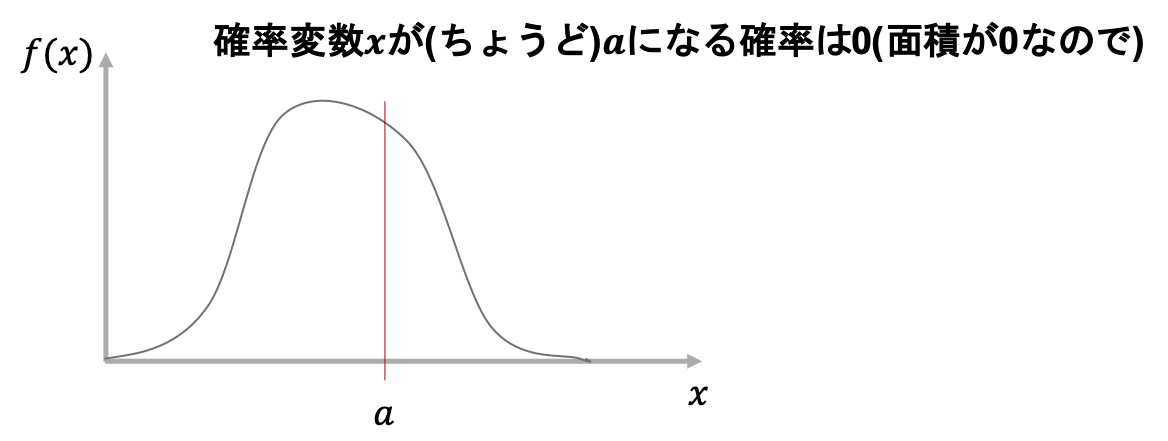
どういうことかというと,例えば日本の成人男性をランダムに1人取ってきて,その人の身長がちょうど170cmである確率は0だということです.
身長は”長さ”なので,連続値です.なので,ぴったし170.00000・・・cmの人なんていないですよね?笑(ちょっと屁理屈っぽいけども)
一方,「170cm~171cmの間」というふうに“区間”で考えれば,確率密度関数の面積は0(確率0%)ではなくなり,値を持つことになります.
ただ,通常身長に限らず,一般的にはデータを保存するときにある程度のところで値を区切ってしまうので(身長ならmm単位まで等),「170cmちょうど」 のデータというのはありますよね.これは連続変数を便宜的に離散変数に変換して扱っているにすぎません.
このように,確率分布の曲線の面積が確率になることから,この曲線の関数を「確率“密度”(関数)」と呼んでいるんですね.
人口密度から人口を計算するように,確率密度から確率を計算できるわけです.
また,通常確率密度関数の全面積は,確率変数が全値をとりうる確率になるので1(100%)となります.
まとめ
今回は推測統計の内容に先駆け,確率変数,確率分布,標本分布,確率密度について解説をしました.
この辺りは普段聞きなれない上に,用語が似ているのでごっちゃにしやすいところなので気をつけましょう.
また,統計学を学習する上で非常に重要な用語なのでしっかり押さえておくといいです.
コミュニティ”DataScienceHub”では,統計学に関する質問なども受け付けております.独学に限界を感じたら是非のぞいてみてください!同じ目的をもった多くの同志が所属しています.(現在450名程度の方々に所属いただいています!)
- 確率変数は,それぞれの取りうる値に確率が対応していて,値が確率的に変動する変数
- 確率分布は,確率変数のそれぞれの値とそれに対応する確率を表したもの.確率変数の分布
- 標本統計量は確率的に変動する確率変数である
- 標本統計量の確率分布を標本分布という(ただたんに,いくつかの標本から計算した統計量の分布ではないことに注意)
- 連続確率変数における確率分布を表す関数を確率密度関数という
- ある区間における確率密度関数が描く曲線の下部分の面積は,確率変数がその区間の値をとりうる確率を表す.
今回は説明が長くなってしまい,Pythonの出番がなかった...orz
次回以降さまざまな確率分布を紹介していこうと思います!
それでは!
追記)次回書きました!様々な確率分布の基礎となる”二項分布”について解説しています!この記事を読めば確率分布についてかなり理解が深まると思います.