Pythonで学ぶデータサイエンス入門:統計編第19回です.
(追記)全16時間の統計学動画講座を公開しました!☆4.8の超高評価をいただいている講座です.こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください.
前回は確率変数や確率分布を紹介しました.
今回から数回に分けて様々な確率分布を紹介していきます.
今回の記事ではその中でも最も基本かつ重要な確率分布である”二項分布”をみていきます.
もう今回の内容をちゃんと理解できたら,確率分布は全然怖くないっす.
でもその前に,もう一度確率分布と確率変数についておさらいをします.まだいまいち理解してない!っていう人もいると思うので・・・!
目次
確率分布は”データ生成装置”だと考えよう
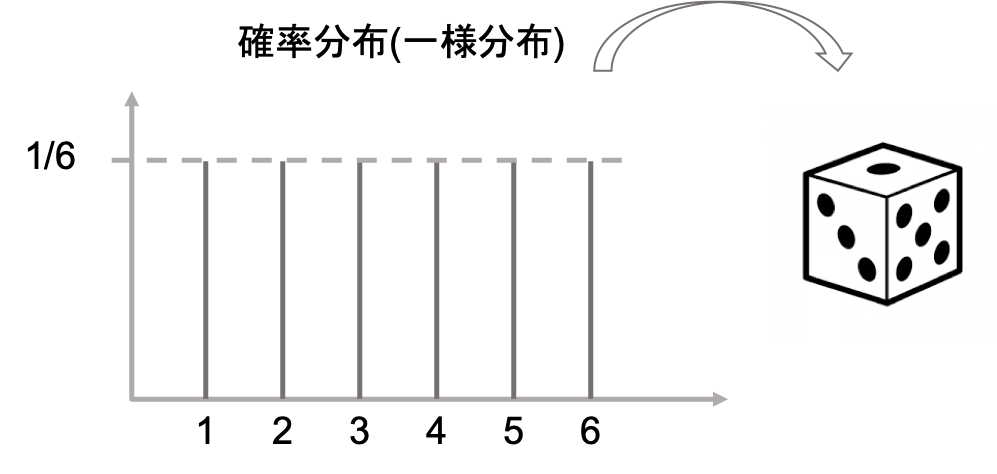
前回の記事同様,サイコロの例をとってみましょう.一つのサイコロを投げて出る目は1〜6になり,それぞれの値がでる確率は1/6です.
この例の確率分布は”一様分布”と呼ばれる確率分布ですが,この(サイコロの例の)一様分布は,1~6の値をそれぞれ1/6の確率で出力できる分布だと考えましょう.
つまり,「サイコロを投げてでた目」というのは.「ある一様分布から生成された値」だということが言えます.
この考え方は確率分布と確率変数を理解するのに非常にわかりやすい考え方なので,理解してください.
そしてこの確率分布は,いくつか決められた”型”があります.
どういう確率分布か(つまりどういう型か)がわかれば,どれくらいの確率でどういう値をとるのかがわかるのです.
これって超便利ですよね?サイコロが上記の確率分布に従うことがわかれば,別に1000回サイコロを振って「どうやら各値1/6の確率でとるらしい」なんて経験的に知る必要はないわけです.
例えば10分に平均3回電話が鳴るコールセンターで,直近10分回に5回鳴る確率はどれくらいか?とか,平均して100個に1個の不良品が発生する生産ラインにて,その製品を1000個単位で箱に梱包した場合1つの箱に1個も不良品が入っていない確率はどれくらいか?とかそういうことがわかるわけです.
ある事象が従う確率分布がわかると,理論的に“これくらいの確率で起こる”というのが言えるようになります.
これってすごい便利ですよね?現実の問題に直結して役に立つのが確率分布なんです!理論的に確率がわかるのは本当に強力です.
今回の記事では様々な確率分布の基本とも言える”二項分布”について紹介していきます.
二項分布は確率分布の祖
確率分布には色々なものが存在するんですが,そのほとんどが今から説明する二項分布からの派生です.(二項分布を基本に少し考え方を変えたり制約をつけたりって感じですね)
二項分布は「1回の観察である事象が起こる確率を\(p\)とします.この観察(や試行)を\(n\)回行った時に,その事象が起こる回数(\(x\))が従う確率分布です.(\(x\)が確率変数です)」

ですよね,具体例をあげてみましょう.
例えばサイコロを3回投げ,2が\(x\)回出る確率を考えてみましょう!この例だと,先ほどの文言は
- 1回の観察→1回サイコロを振る
- ある事象が起こる確率→2がでる確率(つまり1/6)
- \(n\)回行う→3回行う
- \(x\)回起こる→\(x\)回2が出る
という風に対応します.
3回投げているので,2が出る回数は当然0回〜3回です.
それぞれの確率を求めてみましょう.
| 0回 | 1回 | 2回 | 3回 |
| \((\frac{5}{6})^3=\frac{125}{216}\) | \(3(\frac{1}{6})(\frac{5}{6})^2=\frac{75}{216}\) | \(3(\frac{1}{6})^2(\frac{5}{6})=\frac{15}{216}\) | \((\frac{1}{6})^3=\frac{1}{216}\) |
という具合になります.0回と3回は問題ないと思います.2が一回も出ない確率が\(\frac{5}{6}\)でそれが3回続くので\((\frac{5}{6})^3=\frac{125}{216}\)ですね.3回とも2が出るというケースも同じ考え方で,2が出る確率\(\frac{1}{6}\)が3回続くので\((\frac{1}{6})^3=\frac{1}{216}\)です.
2が1回もしくは2回出るパターンは,並び替えの考えが入ってくるので,3を掛けています.例えば2が1回でるパターンは↓
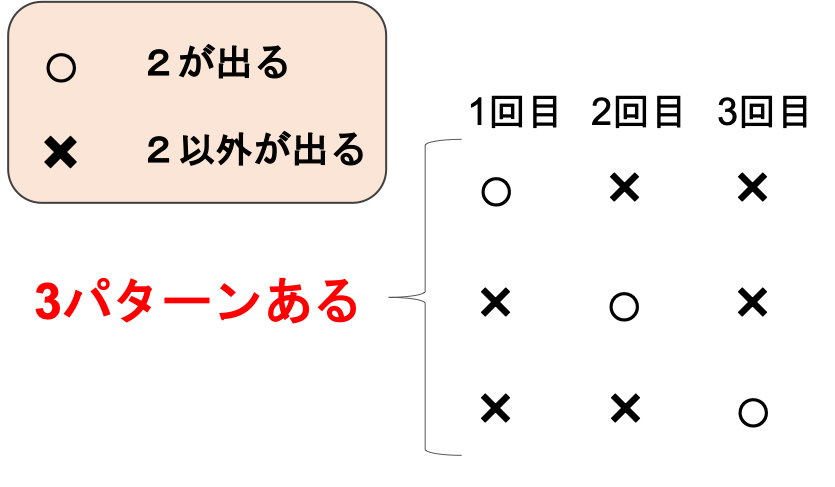
2が2回出る場合も同じように考えればOKです.難しい話ではないですよね?
これを一般化すると,2が\(n\)回中\(x\)回でる組み合わせは\(_{n}C_{x}=\frac{n!}{x!(n-x)!}\)ですね.
\(C\)はCombinationの\(C\)で,組み合わせを表します.この辺りがあやしい人は高校数学をもう一度勉強するといいかも?
以上より,ある事象が起こる確率\(p\)の試行を\(n\)回実施してその事象が\(x\)回おこる確率(これを\(P(x)\)とします)は
$$P(x)=_nC_xp^xq^{n-x}=\frac{n!}{x!(n-x)!}p^xq^{n-x}$$
となります.(ただし,\(q=1-p\)です.つまり\(q\)はその事象が”起きない”確率です)
このような分布を二項分布(binominal distribution)と呼びます.
数式はそこまで重要ではありません.(が,そんなに難しくないので覚えられるレベルです.覚える必要はないと思いますが,二項分布は本当に基本中の基本なので,見慣れておくといいと思います)
重要なのは,「二項分布とはなんなのか」ということで,それは「n回観察してある事象(確率p)がx回起こる確率」を表していると覚えておきましょう!
特に留意しておく点は「回数」に着目した分布だということです!
現実世界でも色々あると思います.サイコロやコイントスはもちろんそうですし,例えばカジノのルーレットでかつ回数なども二項分布で表せます.
今後の記事で説明する確率分布は,この二項分布を基本に色々と制約や派生をした形になっています.この二項分布がきちんと理解できていればそこから他の確率分布をイメージすることが可能なので,しっかり覚えておきまそう!
二項分布において,n=1の時をベルヌーイ分布(Bernoulli distribution)と呼びます.n=1という特別なケースだけ別の名前が付いてるんですね〜
ちなみに,ある試行をして「成功か/失敗か」のような2つの結果しか得られないような試行を,ベルヌーイ試行といいます.ベルヌーイ分布自体がなにかに使われるっていうことは滅多にないので頭の片隅に覚えておきましょう!
Pythonで確率分布から値を生成する
先ほど,確率分布はデータ生成装置だという話をしました.
ここではPythonを使って実際にある確率分布からデータを生成してみようと思います.
実業務でこういったコードを書くことは多くないと思いますが,時々特定の分布からダミーデータを作成したり,試験的にデータを作ってみる必要があったりするので,覚えておきましょう!また,確率分布自体を理解するのにも非常に役立つと思います.
scipyの stats モジュールに様々な確率分布が実装されているので,それらを使います.
二項分布は binom として実装されています.確率分布から値を取ってくる(言い換えると,確率分布に従う確率変数を生成する)には, .rvs() 関数を使います.
rvsは,random variables(確率変数)の略です.
以下のようにして使います.
|
1 2 |
from scipy.stats import binom data_binom = binom.rvs(n=3,p=1/6,size=2160) |
もう一度二項分布がなんなのかを説明すると「1回の観察である事象が起こる確率を\(p\)として,この観察(や試行)を\(n\)回行った時に,その事象が起こる回数(\(x\))が従う確率分布」でした.
n=3, p=1/6ということは,「3回試行して,1/6の確率で起こる事象が\(x\)回起こる確率の分布」ということです.つまり先ほどのサイコロの例でいうと「3回サイコロ振って2の目がでる回数」の事ですね.
では,このdata_binomの中身をみてみましょう
|
1 |
data_binom |
|
1 |
array([0, 1, 1, ..., 0, 1, 1]) |
人によって結果が異なりますが,2160個の数字(0~3)が入っていると思います.
これはサイコロの例でいうと,sample=2160回「サイコロを3回振る」ということをして,それぞれ「2の目が出た回数」の擬似データが格納されています.

なんとなくわかりましたか...?
これがわかれば,先ほどの確率からdata_binomに0, 1, 2, 3がどれくらいの割合で入っているかわかりますよね?
seabornを使って可視化してみましょう(seabornについてはこちら)
|
1 2 3 4 |
import seaborn as sns %matplotlib inline sns.distplot(data_binom, kde=False) |
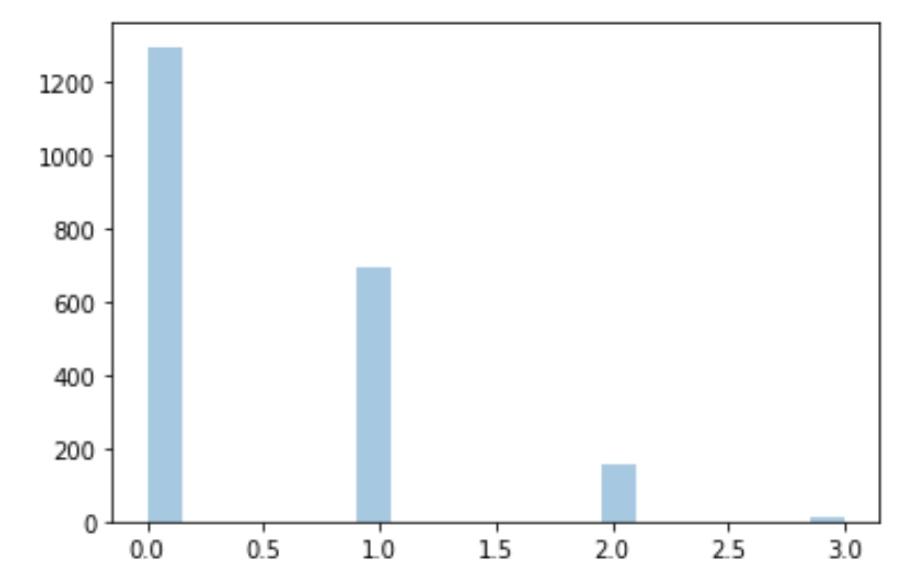
先ほどの確率と見比べてみてください.近い数字になっているかと思います.多くは0回で,3回とも1/6の確率の事象が起こる割合はかなり低くなってますね.
sampleする数を無限にしたら,このヒストグラム(を正規化したもの)は限りなく実際の二項分布の確率分布に近くなります.
実際の業務では,実際に計算することもありますし,このようにデータを作って計算することもできます.誰かへの報告に使うのであれば,このように擬似データを大量に作って,「ほらね?3回とも2が出ることなんて滅多にないんだよ?」と言った方がよっぽど理解が得られるので便利です.
もちろん,「サイコロの出る目」には興味ないと思いますが,現実世界でも二項分布を使える例は腐るほどあります.まぁあらかじめ確率がわかっている事象というのは多くはありませんが,.. ここでは,このようにPythonのコードを書くことによって確率分布からデータを生成できると覚えておいてください.
まとめ
今回は様々な確率分布の超基本となる二項分布を紹介しました.
もうね,今回の記事の内容をしっかり抑えられたらもう確率分布なんて楽勝ですよ....まじで
ってくらい今回の記事は重要だし,今後紹介する確率分布の基礎になります.
- 二項分布は様々な確率分布の基礎となるもの,確率分布の祖とも言えるもの
- 二項分布は,確率\(p\)で起こる事象が\(n\)回のうちに観測される回数(確率変数)\(x\)が従う確率分布
- 確率分布は scipy.stats モジュールに定義されている
- 二項分布は scipy.stats.binorm を使う
- .rvs() 関数を使って確率分布からデータを生成する
- 数式は,,,覚える必要はないと思うけど,二項分布は本当に基本なので頭の片隅にでもおいておくといいかも
こんな感じです!
次回以降はこの二項分布を使って,様々な確率分布を紹介していきます.次回以降紹介する確率分布は,もっと現実世界の問題に使える確率分布なので是非知っておきましょう!絶対に役にたちます!
それでは!
追記)次回記事書きました!二項分布から発展させたポワソン分布という確率分布を解説します.