今回からPythonで学ぶデータサイエンス入門:機械学習編を連載していきたいと思います.(講座全体の説明と目次はこちら)
本連載で学習をする前に,
1.Pythonの基礎
2.データサイエンスのためのPython
3.統計学
この3点はやっておきましょう!是非飛ばさずにStep by stepに取り組んでください.データサイエンスの学習で最も重要なのは「”体系的に”学ぶこと」です.
それぞれの動画講座がありますので,上のリンクから受講いただければと思います
また,機械学習超入門動画講座を公開しております.動画で効率よく学習したい方は↓からどうぞ!(割引クーポンあります).
目次
レベルと範囲
本当にゼロからやっていきます.なので事前の機械学習の知識は一切不要です.
データサイエンティストとして必要な最低限の知識が学べるような講座にする予定で,マニアックな内容は扱いません!
基礎ではあるものの,各アルゴリズムを理解した上でPythonで実装できるようになることを目標にしています.「内容はよくわからないけど実装ができる」ではなくて「内容を理解した上で実装もできる」というレベルを目指します.
範囲は,機械学習の分野で横断的に求められる普遍的な内容(モデルの評価指標や学習方法,bias-variance tradeoff等)に加え,基本的なアルゴリズム(線形回帰,ロジスティック回帰,決定木,SVMなど)の理論と実装を紹介していきます.
機械学習とは

機械学習(ML: Machine Learning)というのは,なんらかのタスク(例えば予測をしたり分類をしたり)をこなすために機械(つまりはコンピュータ)が自動でデータから学習するアルゴリズムやその研究領域を指します.いわゆる「人工知能(AI)」の一分野であり,データサイエンスの中核の技術です.
機械学習の理論のベースは統計学です.機械は“統計的に”最適な解を出すことでタスクをこなしていきます.
この辺りは講座を進めていく上で徐々にわかってくると思います!
じゃぁその学習した機械になにをさせるのか?これは色々あるんですが,大きく以下の3つに分類されます
・回帰(regression): 連続値を予測する.(ex: 将来の売り上げ予測する等)
・分類/識別(classification): カテゴリーやクラス,ラベルと呼ばれる”種類”を判別する. (ex: 病気かどうかを判別する.メールがスパムかどうかを判別する等)
・クラスタリング(clustering): データをカテゴリーやクラス,ラベルと呼ばれる”種類”に分別(グループ化)していく.(ex: 顧客の属性をグループ化する等)
回帰と分類は主に教師あり学習(supervised learning)と呼ばれ,正解のデータ(教師データ)を使って学習していきます.一方クラスタリングは教師なし学習(unsupervised learning)と呼ばれ,教師データなしでデータにラベル付けをしていきます.
例えば病気かどうかを判別するアルゴリズムを機械学習で作る場合,すでに過去の教師データ(病気かどうかのデータ)を学習に使うので教師あり学習です.
一方,自社のWebサイトで商品を購入した顧客を購入履歴をもとにグループ化したいとします.この場合,正解のグループというのはあらかじめわかっているものではないので教師なし学習になります.
予測モデルを構築する
例えば,ある不動産の月の家賃を推測したいとします.自分が持ってるマンションを貸しに出したいとか,逆に今賃貸物件を探しているなんて場合を想定してみてください
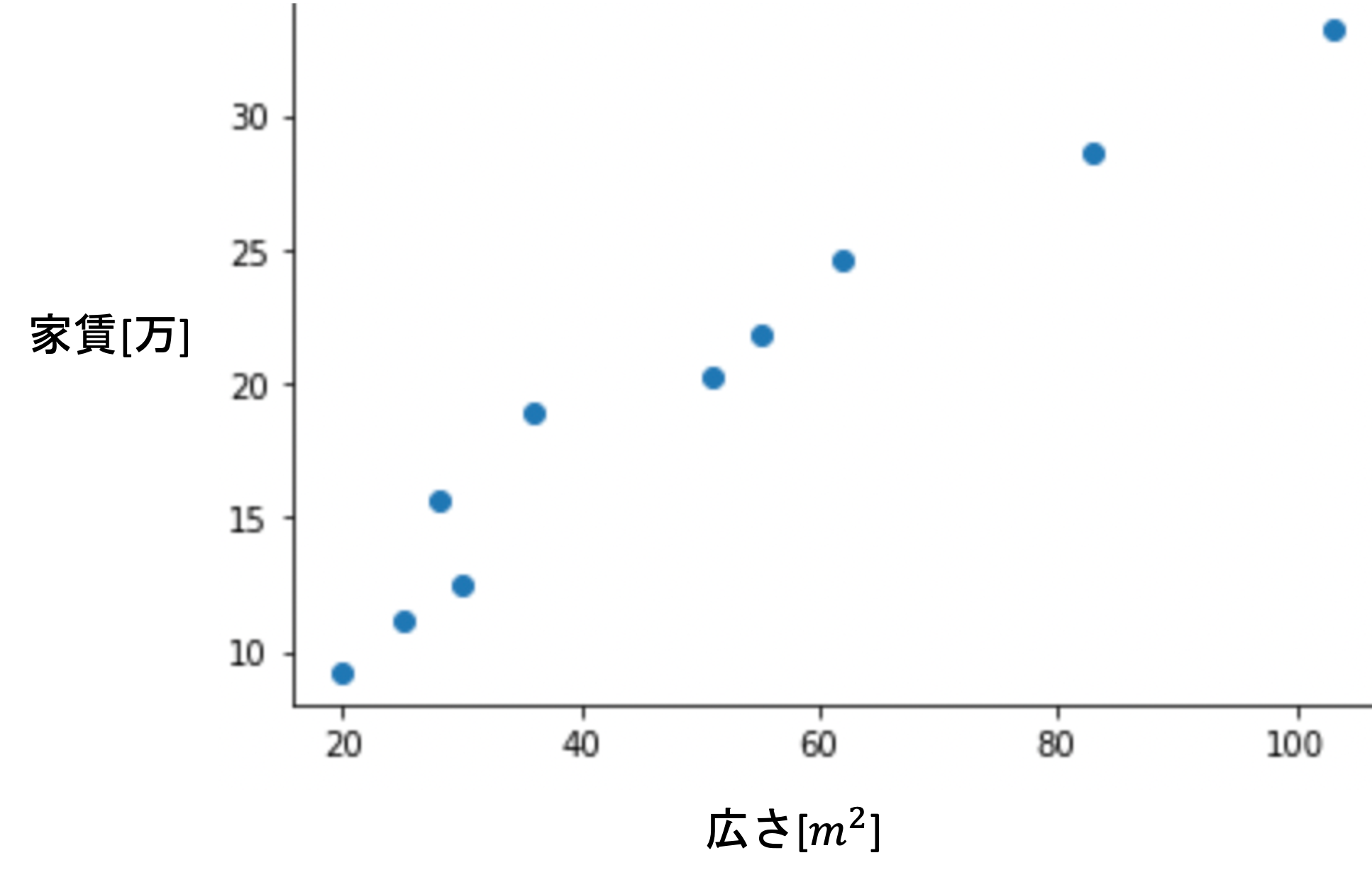
今,上のようなデータがあったとします.(仮に,近くの不動産10件をランダムにピックアップして調べたとしましょう)
それぞれの物件の広さ(平米数)と家賃には相関がありそうです.つまり,広さがわかればある程度家賃を推測できると考えられます.
すでにある10件のデータから,「広さ」の情報をもとに「家賃」を推測することができる「モデル」を構築します.これを一般に「学習する」といい,「推測する」ことを「予測する」というのが一般的です.
学習に使う10件のデータのことを学習データ(training data)と呼びます.この10件のデータはランダムにとってきたデータなので,この背後には母集団のデータセットがあることを意識しておきましょう.(この辺りは推測統計の記事でも解説しましたね)
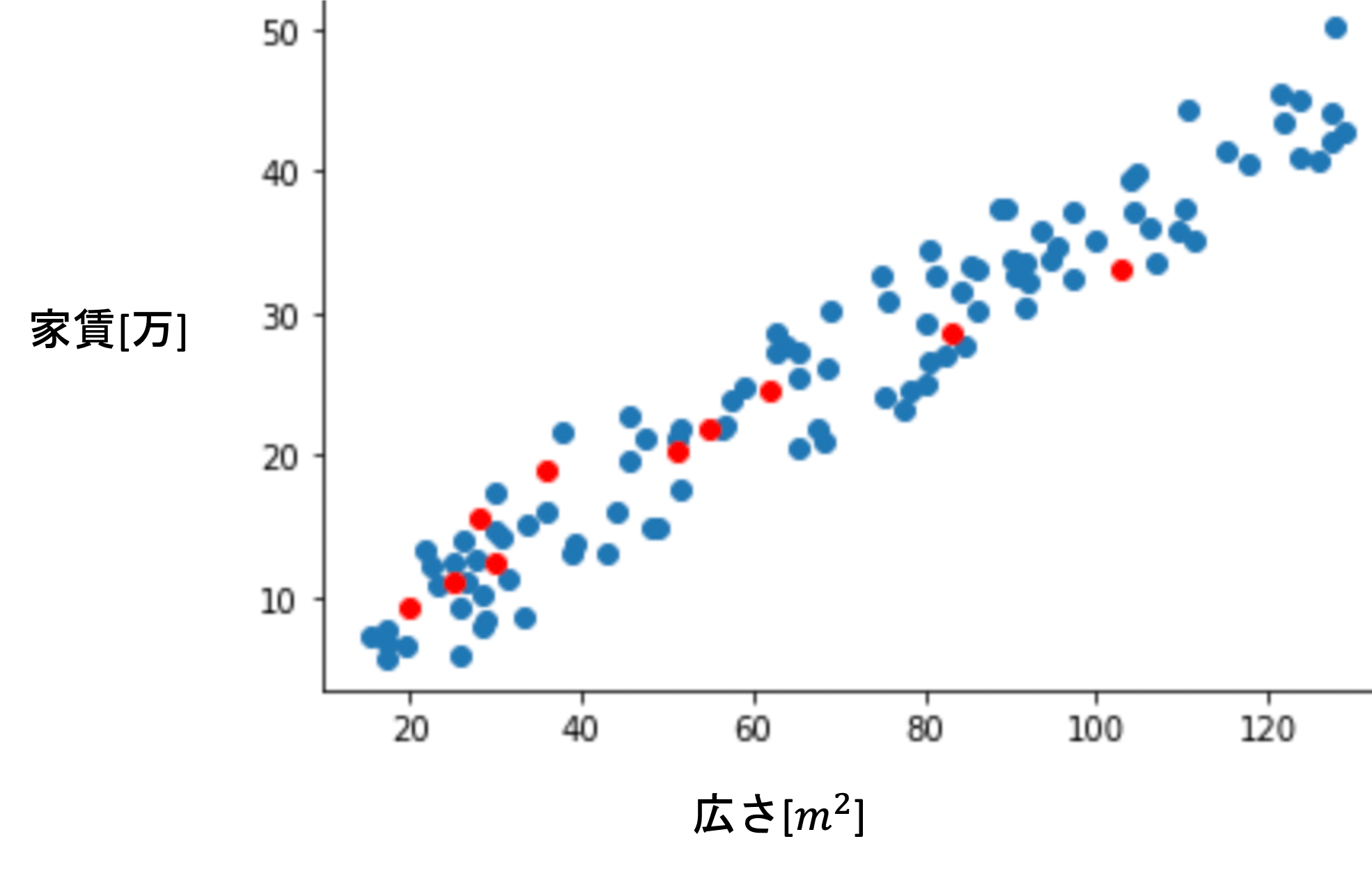
例えば青い点が母集団のデータだとした場合,今回たまたま学習データとして用意できたのが赤い点の10件の不動産データということです.(これはイメージです.実際に母集団がどのように分布しているかはわかりません.)
広さ[\(m^2\)]を\(X_1\)とし,家賃[万]を\(Y\)とすると,これら二つの変数の間には何かしらの関係があるとし以下のような式で表せると考えることができます.
$$Y=f(X_1) + \epsilon$$
\(f(X_1)\)は\(X_1\)を引数とした何かしらの関数という意味です. \(\epsilon\)はエラー項や誤差項(error term)と呼ばれるもので,\(Y\)のうち\(X_1\)では説明できない部分です.(例えば今回の例では,広さでは説明できない家賃の部分があるはずです.これを一律エラー項としておきます.)
つまり今回の例では「家賃」を,「広さを引数にした関数」+誤差で表しているということですね!
これは,「広さ」で「家賃」を”説明している”と考えることもできるため,\(Y\)を目的変数,\(X\)を説明変数という話は統計学講座第13回でもしました.(他にも独立変数と従属変数などといったりもします.)
今回の講座では説明変数のことを特徴量(feature)と呼びたいと思います.(目的変数を特徴付ける変数という意味で特徴量と呼ぶことが多いです.機械学習の文脈では最も一般的な呼び方かと思います)
また,一般に「家賃」を特徴付ける特徴量は「広さ」以外にも「築年数」や「駅からの距離」など,他にも多くの特徴量があると考えられます.
なので先ほどの式をもう少し一般的に書くと,\(X=X_1, X_2, …, X_n\)とし,n個の特徴量があるとすると
$$Y=f(X) + \epsilon$$
のように表すことができます.
機械学習では,手元にある学習データを使って\(f(X)\)を推測することを目指します.(推測した\(f(X)\)を\(\hat{f}(X)\)としておきます.推測値に^(ハット)をつけるのは統計学ではおなじみですね!).つまり,
$$\hat{Y}=\hat{f}(X)$$
で表される\(\hat{Y}\)を求めるためのモデルを構築することになるのです.(\(\hat{Y}\)は\(Y\)の推測値,つまりは予測値です.また,ここでは真のエラー項\(\epsilon\)は出てきません.これは\(X\)とは独立したものであり,学習データからは学習することができないため,どう頑張っても\(\epsilon\)を計算することはできないからです)
「機械学習では真の\(f(X)\)を推測する」
以上のことを常に頭に入れながら本講座を進めてください!
これをどのようにして行うのか?これには色々なアルゴリズムがありますが,線形回帰(linear regression)が最も基本的なアルゴリズムなので,今回の記事から数回に分けて線形回帰について解説していきます.
線形回帰が最も基本的なアルゴリズム
機械学習には色々なアルゴリズムがありますが,”線形回帰”というアルゴリズムが最も基本的なアルゴリズムで,他の多くのアルゴリズムがこのアルゴリズムの派生だったり欠点を補うものだったりします.
なのでまずは線形回帰について解説をしていきます.(線形回帰については統計学講座でも何回かにわたって基礎を解説してます.重要な概念について触れているので一度こちらも読んでみてください!)
↑の記事で解説した通り,線形回帰は以下の式で表されるんでした.
$$\hat{y}=a+bx$$
つまり先ほどの\(Y=f(X)+\epsilon\)において,線形回帰では\(f(X)\)を\(a+bx\)という形(モデル)で仮定していることになります.
アルゴリズムによってどのような式で\(f(X)\)を表すか変わってきます.他のアルゴリズムでは別の数式を使って\(f(X)\)を推測していきます.また,数式を使わないで推測していくアルゴリズムもあります(今後説明するKNNというアルゴリズムはその一例です).線形回帰のように数式を使って当てはめていく手法をパラメトリック(parametric),数式を使わない手法をノンパラメトリック(non-parametric)と言います.
機械学習では多くの特徴量が出てくるので,\(a+bx\)の形では扱いにくいです.なので以下のように書き換えて説明します.
$$f(X)=\theta_0+\theta_1X_1+\theta_2X_2+\cdots+\theta_nX_n$$
特徴量\(X\)が\(X_1, X_2, .., X_n\)のようにn個あるケースです.\(\theta_0, \theta_1, \theta_2…, \theta_n\)は係数です.つまり,線形回帰では,これらの係数を推測していくことになります.今回の特徴量は「広さ」のみなので,\(f(X)=\theta_0+\theta_1X_1\)ですね.
係数\(\theta_0\)および\(\theta_1\)は,最小二乗法(least square)によって求めることができることを統計学講座第13回で解説しました.(この辺り覚えていない方は是非もう一度読み直してみてください!)
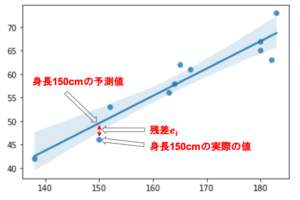
最小二乗法というのは,「実際の値と予測値のずれが最小になるように回帰直線を引くこと」という至極当たり前のことをしているんでしたね.(統計学講座第13回参照
特徴量が1個であれば直線になるし,2個の場合は3次元空間になり平面になります.3個以上の場合は平面をn次元で一般化した超平面と呼ばれるものになりますが,考え方は同じです.多次元についてはまた今後の記事で扱っていくので今は二次元で考えてください
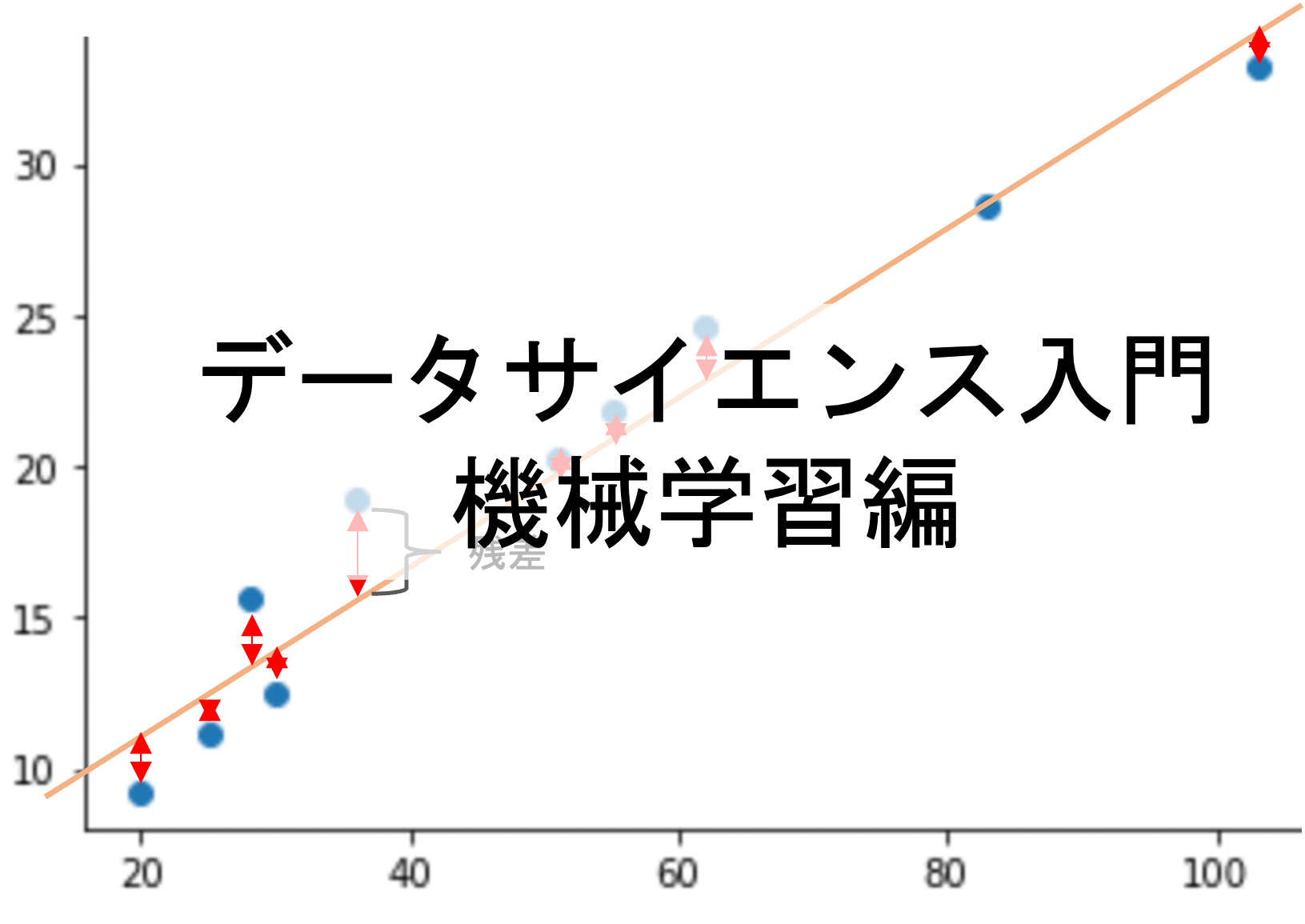
これをどのようにするかというと,実際の値と予測値のずれ=残差として,それぞれのデータの残差(=\(e_i\))の2乗和が最小になるように線を引くんでした.数式で表すと以下のようになります.(特徴量の数をnにしているので,本講座では学習データの数をmで表します)
$$\sum^{m}_{i=1}{e_i^2}=\sum^{m}_{i=1}{\left\{y_i-(\theta_0+\theta_1x_i)\right\}^2}$$
\(x_i\)は各データの値を表します.(今回の例では各データの「広さ」です)
例えば先の10件の学習データに対して以下のように直線(つまりは\(f(X)=\theta_0+\theta_1X_1\)の形です)を引いてみた時に,残差(下の図の赤い矢印)の二乗和が最小になる直線が最小二乗法を使った時の線形回帰の結果になります.(下の図では適当に線を引いています.)
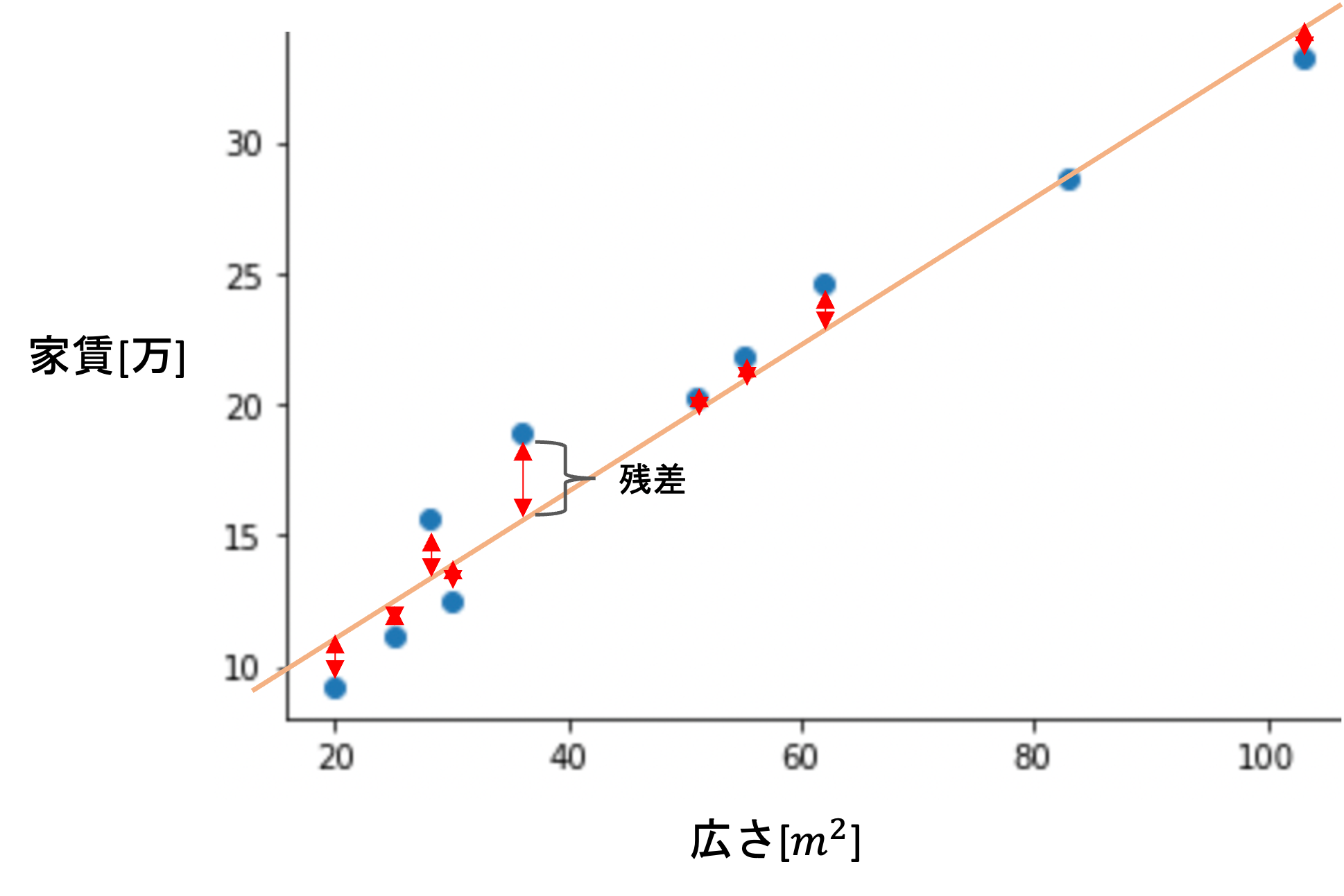
ここまでは統計学講座でも解説した内容ですが,では具体的にどのようにして残差の二乗和が最小になるような直線を求めることができるのでしょうか?適当に線を引いて残差の二乗和を計算して,もっと小さくなるように直線を引き直して...とするにも,どのように直線を引いていけばいいかわかりません.
ここで,機械学習らしい「学習アルゴリズム」が必要になってきます.(※線形回帰では学習アルゴリズムを使わずに計算で一発で出す方法もあります.それについてはまた今後解説していきます.
次回の記事では,具体的にどのようなステップで学習を進めていくのかを解説します.
まとめ
今回の記事から機械学習講座を連載していきます.今回はその第一発目の記事として「機械学習とはなにをするのか?」について話をしました.
- 機械学習とは,学習データから機械が自動で学習してタスク(回帰,分類,クラスタリング等)を行うアルゴリズムのこと
- 回帰と分類は教師あり学習と呼ばれ教師データから学習をし,クラスタリングは教師なし学習と呼ばれ,正解の情報がない状態で学習をするアルゴリズム
- 目的変数と説明変数は\(Y=f(X) + \epsilon\)の形で表され,機械学習では\(f(X)\)の推測値である\(\hat{f}(X)\)を求める
- 線形回帰が最も基本的な機械学習のアルゴリズムであり,残差の二乗和が最小になるように直線(3次元の場合は平面, 4次元以降では超平面(平面をn次元で一般化したもの))をひく
それでは,次回の記事では具体的にどのように最小二乗法を使って直線を求めていくのか解説していきます!「機械が学習する」というまさに機械学習の中核となるアルゴリズムなのでしっかり解説していきます!
追記)次回の記事書きました!↓