回帰分析を図でわかりやすく解説！条件付き平均と最小二乗法って？【統計学入門13】

Pythonで学ぶデータサイエンス入門：統計編第13回です．

（追記）全16時間の統計学動画講座を公開しました！☆4.8の超高評価をいただいている講座です．こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください．

前回までの記事で２変数間の相関関係をあらわす相関係数についてみてきました．

今回はこの相関係数ととても密接に関わっている‘回帰”(regression)について話していきます．回帰は機械学習にも繋がるトピックであり，データサイエンスの一番の基礎ともいえる部分なので，しっかり押さえておきましょう！

今回の記事では

• 回帰は条件付きの平均
• 最小二乗法

を理解していきたいと思います．

それではみていきましょう！

回帰ってなに？

前回までの記事で相関係数をみてきましたが，相関係数はあくまでも，「ある変数の値が高いと，もう片方の変数の値も高い(あるいは低い)傾向にある」ということがわかるものであって，「ある変数の値がどれくらい高いと，もう片方の変数の値もどれくらい高く(あるいは低く)なるか」という”程度”の話はしていませんでした．

これがわかるようになると，ある変数の値がわかった時，もう片方の変数の値の検討がつけられますよね？つまり「予測」を立てることができるわけです．昨今のデータサイエンスの理由の１つには，このように，ある変数の値から別の変数の値を予測することができ，それが現実世界において重宝するという背景があります．

例えば家の価格を決める際に，築年数や家の広さ，駅からの距離などの変数から，だいたいの家の価格を予測できたら買い手も売り手も便利ですよね？

さて，「だいたいの家の価格」ってなにを指しているんでしょうか？

これは，築年数や家の広さ，駅からの距離などの変数がある値だとしたときの，平均の家の価格のことです．

もっとシンプルな例で考えてみましょう．前回までの体重と身長の例で考えると，例えば身長から体重を予測することを考えてみましょう．

この場合，例えば身長170cmである場合の平均的な体重を予測できるわけです．

このように，「身長が170cm」という条件付きでの体重の平均を，「条件付き平均」と呼びます．

回帰は，この条件付き平均を求めるものなんですね！

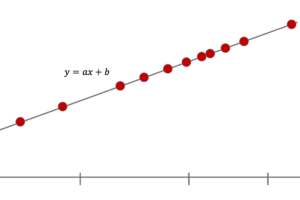
式にするとこんな↓な感じになるはずです．(直線で表せると仮定しておきます．)

$$\hat{y}=a+bx$$

\(\hat{y}\)は，\(x\)に対する\(y\)の条件付き平均です．これはつまり，\(x\)から\(y\)を予測しているわけです．これを「\(y\)の\(x\)への回帰直線(regression line)」と呼びます．(回帰直線を線形回帰(linear regression)とも言うことがあります．英語だとこっちの方が一般的な気がします．)

\(y\)の式なので「\(y\)の」であることはわかると思います．そして，xの値を使って書き直線を引くことになるので「\(x\)への」(\(x\)に対しての)という風に解釈すればOKです．

例えば前回までの例で，weight(体重)のheight(身長)への回帰直線を引くと以下のようになります．

(回帰直線は，seabornの regplot() を使って簡単に描画することができます．)

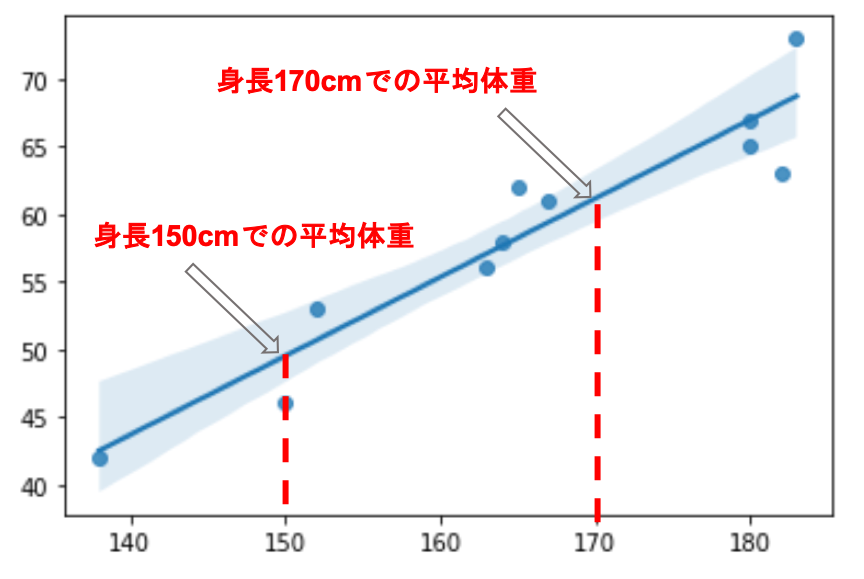
この直線上の値は，各体重での身長の条件付き平均を表しています．

例えば身長150cmに対して，データには46kgという値があります．が，回帰直線ではあくまでも「与えられたデータを元に平均的な値を算出した」までにすぎず，当然実際のデータと差がある場合がほとんどです．(身長150cmで体重48kgあたりって，，，ちょっとデータがリアルではないですが，気にしないでくださいw)

変数\(x\)が変数\(y\)の平均値を決定するわけですが，この変数\(x\)のことを回帰変数(regressor)，変数\(y\)のことを被回帰変数(regressand)と呼びます．これには他の組み合わせの呼び方もあって，変数\(x\)と変数\(y\)をそれぞれ独立変数(independent variable)，従属変数(dependent variable)と呼んだり，目的変数と説明変数と呼んだりします．(実験等で得られたデータは前者，調査等で得られたデータは後者のように呼びますが，実際区別してる人は少ないように思います．)

このように直線を引いたりすることで回帰の関係を分析することを一般に回帰分析(regression analysis)と呼ぶので覚えておきましょう！

直線の式はどうやって決めるの？→最小二乗法

さて，

回帰直線を引くことによってある変数の値から他の変数の値を予測することができることはわかった．

それが便利であることもわかった．

そしてその直線を\(y=a+bx\)で表すこともわかった．

でもその直線をどうやって求めるのよ

\(y=a+bx\)の\(a\)と\(b\)の値が決まれば回帰直線を引けるわけですが，どのようにして線を引くのでしょうか？どのようにして\(a\)と\(b\)を決めればいいのでしょうか？

これには，最小二乗法(least squares method)と呼ばれる手法を使って求めていきます．非常に重要なので絶対に覚えておきましょう．

サイショウジジョ・・・やだもう帰ってシャワー浴びてビール飲んで寝たいorz

わかります．もうね，名前がイケてないんですよ．統計学って全体的にネーミングセンスない(というか専門用語感丸出し)ので初学者の人は単語みただけでもうやめたくなりますよね？

でもこれ，やってることはめちゃくちゃ簡単なんです！！

一言で言うと，「実際の値と予測値のずれが最小になるように回帰直線を引くこと」です．

当たり前ですね．

さて，「実際の値と予測値のずれ」とはなんでしょうか？以下の図でみてみましょう

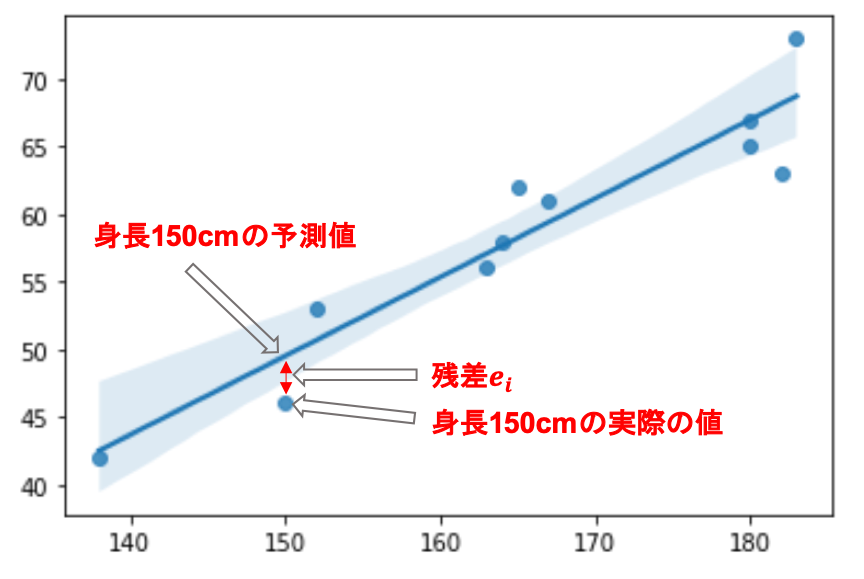
例えば身長が150cm(つまり\(x=150\))の予測値(\(y=a+b\times150\))と実際の値「46」とのずれがを残差と言い，\(i\)個目のデータにおける残差を\(e_i\)で表します．

この\(e_i\)を全てのデータにおいて計算していき，その合計が最小となるように線を引くわけです．

しかし，予測値の方が実際の値より大きかったり小さかったりするので，単純に「予測値　-　実際の値」のようにすると正になったり負になったりして厄介ですよね？こういう時は，おきまりの”２乗”です．統計学では絶対値の計算は好まれないので，このような「差の大きさ」を扱う時は基本的に2乗します．(こちらの記事でもそういう話をしました)

式で書くと以下のようになります．

$$\sum^{n}_{i=1}{e_i^2}=\sum^{n}_{i=1}{\left\{y_i-(a+bx_i)\right\}^2}$$

これを最小にするaとbを求めればいいわけです．aとbでそれぞれ偏微分した結果を連立方程式にしてとけば，aとbを求めることができます．導出は別に重要ではないと思うのでここでは割愛しますが，重要なのは，「残差の２乗を最小にするように線を引く」ということと，「これを最小二乗法という」というところですね！

さて，この最小二乗法でaとbはどのような値になるのでしょうか？

少し長くなってきたので，続きは次回の記事に書きます！

まとめ

今回は回帰分析について解説しました．回帰分析は現実世界の様々な問題にアプローチすることができます．データサイエンスの最も基本的なアルゴリズムの１つなのできちんと押さえておきましょう！

• 回帰は条件付き平均
• 回帰直線はy=a+bxのように表す
• 回帰直線は残差の二乗を最小にするように引く（最小二乗法）

次回はPythonを使って実際に回帰直線の式を求めてみたいと思います！実際にPythonをつかって求めるやり方も紹介します

それでは！

(追記)次回書きました！

回帰直線の数式をイメージで理解する．回帰係数と相関係数の関係【統計学入門14】