正規方程式を完全解説(導出あり)【機械学習入門4】

こんにちは，米国データサイエンティストのかめ(@usdatascientist)です．

今回の記事はデータサイエンス入門の機械学習編第4回です．(講座全体の説明と目次はこちら)

追記)機械学習超入門動画講座を公開しました！動画で効率よく学習をしたい人はこちら(現在割引クーポン配布中です)

第2回の記事と第3回の記事で，具体的にどうやって線形回帰のモデル($\hat{f}(X_1)=\theta_0+\theta_1X_1$)を求めるのかを解説し，損失を最小になるようなパラメータを最急降下法という勾配法のアルゴリズムを使って求めていきました．

今回は，最急降下法を使わずに解析的に(つまり，数式を変形して)解を求める方法を紹介します！

単純な線形回帰では，こちらの解法を使われることがほとんどだと思います．なので，正規方程式は機械学習で非常に重要な項目の一つなのでしっかり解説していきます！それでは見ていきましょ〜

1 正規方程式(normal equation)
2 正規方程式を使って線形回帰をしてみる
3 正規方程式の注意点
4 まとめ

正規方程式(normal equation)

解析的に求めるには，正規方程式(normal equation)という式を使っていきます．

まずは第2回で紹介した損失関数(線形回帰ではMSE)の式

$$L(\theta)=MSE=\frac{1}{m}\sum^{m}_{i=1}(y_i-\hat{y_i})^2$$
(ただし，$\hat{y_i}$は$y_i$に対応する予測値で$\hat{f}(x_i)$の結果で，$\hat{f}(x_i)=\theta_0+\theta_1X_1+\cdots+\theta_nX_n$であり，$X_i$は各データ$x_i$の各特徴量ベクトルです．また，簡単のため$\theta=\theta_0, \theta_1, \cdots, \theta_n$としています．)

をみてみましょう．これをそれぞれのパラメータ$\theta_i$で偏微分した値が0になる$\theta$が解となります．(最急降下法を思い出してみてください．勾配がなくなったところで学習が終わり，そこを解としていたんでした．また，今後の指揮導出を簡単にするために，微分するのは平均だろうと合計だろうと変わらないので，損失関数の$(y_i-\hat{y_i})^2$に着目します．)

これを行列を表して書いてみましょう！

補足
機械学習では，データ数や特徴量の数が複数になるため，よく行列を使って表すことが多いです．この辺りは「線形代数」という数学の分野になります．「行列演算が全く分からない！」という形は是非一度線形代数の勉強をしてみてください．おすすめの本をこちらで紹介しているので参考にしてください

上記では各データの値を$x_i$としていましたが，特徴量が複数ある場合は$x_{ij}$とし，$j$番目の特徴量の$i$番目のデータという風にしておきます．(なので例えば第1回の記事の例で「広さ」という特徴量を1番目とすると，各データの「広さ」の値は$x_{i1}$と表せます．また，書きやすくするために，0番目の特徴量$x_{i0}$は全て1とし，線形回帰の係数$\theta_0$に対する特徴量としておきます)

すると，それぞれのデータに対する予測値は以下のように書くことができます．

$$
\begin{bmatrix}
\hat{y}_1 \\
\hat{y}_2 \\
\vdots \\
\hat{y}_{m-1} \\
\hat{y}_m \\
\end{bmatrix}
=
\begin{bmatrix}
x_{10} & x_{11} & \cdots & x_{1n-1} & x_{1n} \\
x_{20} & x_{21} & \cdots & x_{2n-1} & x_{2n} \\
\vdots & \vdots & \cdots & \vdots & \vdots \\
x_{m-10} & x_{m-11} & \cdots & x_{m-1n-1} & x_{m-1n} \\
x_{m0} & x_{m1} & \cdots & x_{mn-1} & x_{mn} \\
\end{bmatrix}
\begin{bmatrix}
\theta_0 \\
\theta_1 \\
\vdots \\
\vdots \\
\theta_{n-1} \\
\theta_n \\
\end{bmatrix}
$$
つまり，それぞれの行列およびベクトルを$\mathbf{\hat{y}}$,$\mathbf{X}$,$\mathbf{\theta}$とすると$$\mathbf{\hat{y}}=\mathbf{X}\mathbf{\theta}$$と表せます

先ほどの損失関数$L(\theta)$の$\sum^{m}_{i=1}(y_i-\hat{y_i})^2$も同様に

$$
\begin{align*}
\sum^{m}_{i=1}(y_i-\hat{y_i})^2&=(\mathbf{y}-\mathbf{X}\mathbf{\theta})^T(\mathbf{y}-\mathbf{X}\mathbf{\theta})\\
&=(\mathbf{y}^T-\mathbf{\theta}^T\mathbf{X}^T)(\mathbf{y}-\mathbf{X}\mathbf{\theta})\\
&=\mathbf{y}^T\mathbf{y}-2\mathbf{\theta}^T\mathbf{X}^T\mathbf{y}+\mathbf{\theta}^T\mathbf{X}^T\mathbf{X}\theta
\end{align*}
$$

補足
$\mathbf{y}^T\mathbf{X}\mathbf{\theta}$は計算するとスカラー(行列ではないただの単一の値)になります．つまり，この行列演算の転置をとっても同じです．$\mathbf{y}^T\mathbf{X}\mathbf{\theta}=(\mathbf{y}^T\mathbf{X}\mathbf{\theta})^T=\mathbf{\theta}^T\mathbf{X}^T\mathbf{y}$となります

と表せることができ，これを$\theta$で偏微分して0になることで得られる$\theta$を考えると
$$
\begin{align*}
-2\mathbf{X}^T\mathbf{y}+2\mathbf{X}^T\mathbf{X}\theta=0
\end{align*}
$$

これを解くと

$$\theta=(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y}$$

となります．これが正規方程式と呼ばれるもので，学習データの$\mathbf{X}$と$\mathbf{y}$をこの式にぶち込めば一発で答えがでます．(素敵！！)

補足
対称行列$\mathbf{P}$としたときの$\theta^T\mathbf{P}\theta$の$\theta$に対しての微分は2$\mathbf{P}\theta$になります．$\mathbf{X}^T\mathbf{X}$は対称行列になるため，同様にこちらの公式を適用できます

なにがなんだかさっぱりわかりませんでした！

行列演算や微分を学習していない人からすると「？？？」な部分もあると思いますが，今はあまり気にせず「このように一発で求める方程式がある」と覚えておけばOKです．上記の導出はわかる人向けだと思ってください．

ただ，正規方程式はかなり有名な公式なので，式を覚えてしまってもいいくらいです．

正規方程式を使って線形回帰をしてみる

それでは早速，正規方程式を使って線形回帰をしてみましょう．興味がある人は簡単なデータを使って手計算してみてもいいですが，業務で実際に求められるのはPythonなどのプログラミング言語を使って実装できることです．

線形回帰はscikit-learnというライブラリを使って，簡単に求めることができるんですが，今回は練習も兼ねて自分で正規方程式を作って求めてみましょう◎

本ブログでは基本的にPythonを使っていきます．環境構築はDocker+JupyterLabを使ったやり方をこちらの記事で紹介しているので参考にしてみてください．

また，PythonについてはPythonの基礎が学べる動画講座と，データサイエンスに必要なPythonの講座があるので，是非どちらも受講ください！
↓Python基礎

【決定版】Python入門動画講座を公開しました【超高評価でベストセラー】

↓データサイエンスのためのPython

【公開初日で受講生1000人超え！】データサイエンスのためのPython動画講座を公開しました【全23時間…!!】

どちらも☆4.8を記録しているUdemyで最も評価が高いPython講座です．(本講座では上記のPython講座およびデータサイエンスのPython講座の知識を既知のものとして進めていきます．未受講の方は先に受講しておくことをお勧めします．記事にクーポンを貼っている場合があるので是非ご確認ください)

1.データ取得

今回は実際のデータを使ってやってみましょう！
seabornの load_dataset メソッドを使います．(seabornについてはデータサイエンスのためのPython講座第24回以降でも解説してます！)

また，load_datasetメソッドを使うやり方は統計学の動画講座と同じですね！

データのファイル名を指定すると，DataFrameの形でデータをとってこれます．(データの一覧はこちら)

本記事ではDiamondsデータセットを使って練習してみましょう！(DataFrameの基本的な使い方はデータサイエンスのためのPython講座第11回以降をご参照ください)

import numpy as np
import pandas as pd
import seaborn as sns

df = sns.load_dataset('diamonds')
df.head()

import numpy as np

import pandas as pd

import seaborn as sns

df = sns.load_dataset('diamonds')

df.head()

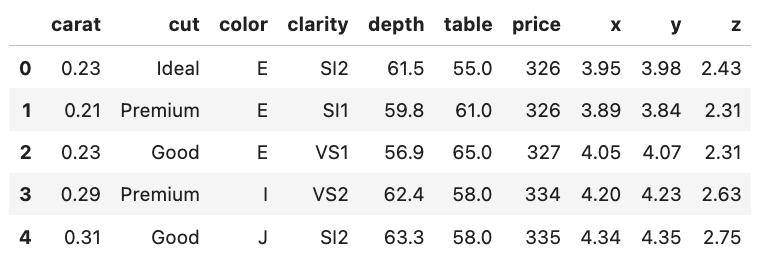
すると，このようなデータであることがわかります．

priceはドル，caratはダイアモンドの重さを表す指標で，カラットですね．cutはカットの質(Fair, Good, Very Good, Premium, Ideal)で，colorは色のグレード(Jが最低でDが最高), clarityは透明度(I1 (最低), SI2, SI1, VS2, VS1, VVS2, VVS1, IF (最高))で，x, y, zがそれぞれダイヤのサイズをmmで表しています．depthは幅に対しての深さの割合(2 * z / (x + y))でtableはダイヤの表面(一番上の最も広い面)の全体の幅に対する割合です．

補足
実際の業務でデータを扱う際は，データ項目の意味やデータの取ってき方など，注意を払って確認する必要があります．例えばこれらは全て同じ人によって計測されたのか，卸売り価格なのか小売価格なのか，国や地方はどうなっているのかなどを考える必要があるかもしれません．が，本講座ではアルゴリズムの練習が目的なのでこの辺りは今は気にしません

興味がある人は本データセットのヒストグラムなどを確認してみてください．(本記事ではスペース節約のため .describe() でデータ全体の分布を把握します．)

2.全体のデータの分布の確認と異常値の対応

df.describe()

1	df.describe()

.describe()でデータ全体の分布を確認することができるんでした．すると，x, y, zカラムの最小値が0になっています．これは異常値だと思うので排除しておきましょう．

df = df[(df[['x','y','z']] != 0).all(axis=1)]
len(df)

1 2	df = df[(df[['x','y','z']] != 0).all(axis=1)] len(df)

53920

53920

20件ほどのレコードを排除しました．今回はシンプルにしたいので，caratカラムを特徴量としてpriceを予測する線形回帰を正規方程式$(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y}$を使って作ってみましょう.

まずはcaratとpriceのscatter plotを見てみましょう

import matplotlib.pyplot as plt
%matplotlib inline
carat = df['carat'].values
price = df['price'].values

plt.scatter(carat, price, alpha=0.1)
plt.xlabel('carat')
plt.ylabel('price')

import matplotlib.pyplot as plt

%matplotlib inline

carat = df['carat'].values

price = df['price'].values

plt.scatter(carat, price, alpha=0.1)

plt.xlabel('carat')

plt.ylabel('price')

んー，カオス！！笑
まぁ実際のデータなんてこんなもんです．この図からパッと見わかることとしては，caratだけでpriceを説明するのは難しそうですが，相関は間違いなくあるので，ある程度線形の関係にもってけそうではあります．また，このデータセットはある金額以上のデータは除いているように見えます(priceの上限が設定されているように見える)．これは，本来そのような上限がない場合に比べ，回帰の結果が変わってくることを念頭に置いておきましょう．

3.正規方程式実装

まず$\mathbf{X}$を以下のようにして組み立てます．

X = np.vstack([np.ones(len(carat)), carat]).T
X

1 2	X = np.vstack([np.ones(len(carat)), carat]).T X

線形回帰のモデル($\hat{f}(X_1)=\theta_0+\theta_1X_1$)の$\theta_0$に対応する特徴量は全て1となるので，np.ones()を使って要素が1の行列を作ります．また，それをcaratの特徴量とnp.vstack()を使って結合し，それを先の行列$\mathbf{X}$の形にするために .T で転置をします．(難しく思えるかもしれませんが，一つ一つ実行して形を確認しながらやってみてください．)

それでは，正規方程式$(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y}$を使って最適な$\theta$を求めてみます

y = price
theta_best = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)

1 2	y = price theta_best = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)

y には price をそのままセットすればOKですね

逆行列を求めるには np.linalg.inv() を使えばOKです．linalgはlinear algebra(線形代数)の略で，線形代数の演算に便利な関数が入っています． inv はinverse(逆)の略なのでわかりやすいですね．行列の積は .dot() メソッドで演算することができます．

補足
.dot() メソッドは，ベクトル(1次元配列)同士に対して使うと内積(ドット積)を計算しますが，多次元配列については内積ではなく普通の積演算になることに注意しましょう．

すると，theta_bestは[-2255.76878704, 7755.76725406]となっているのがわかると思います．

つまり，正規方程式の結果$price=-2255.76878704+7755.76725406\times carat$という回帰直線が求まったわけです．

4.結果の可視化

これを先ほどのscatter plotに合わせてplotしてみると

x_axis = np.linspace(0, 3, 10)
y_pred = theta_best[0] + theta_best[1]*x_axis

plt.scatter(carat, price, alpha=0.1)
plt.plot(x_axis, y_pred, 'red')
plt.xlabel('carat')
plt.ylabel('price')

x_axis = np.linspace(0, 3, 10)

y_pred = theta_best[0] + theta_best[1]*x_axis

plt.scatter(carat, price, alpha=0.1)

plt.plot(x_axis, y_pred, 'red')

plt.xlabel('carat')

plt.ylabel('price')

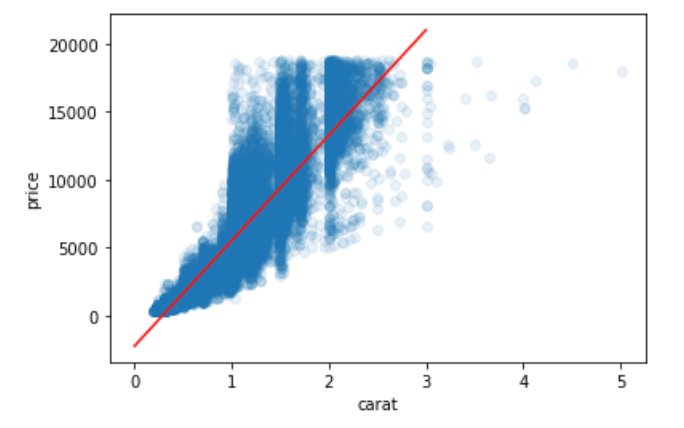
確かにplotしてみると，全体のデータの分布を汲み取った結果になってそうですね!

実際の業務で正規方程式をスクラッチで実装することはないと思いますが，あまりにも有名な方程式なので実際にPythonで一度は実装してみてもいいと思います! また，データサイエンスでは行列演算をスクラッチで実装することはよくあります．いい練習になったのではないでしょうか◎

正規方程式の注意点

一発の数式でパッと解を出せる素敵な正規方程式ですが，いくつか注意点があります．

1. 特徴量の数nが多すぎると$(\mathbf{X}^T\mathbf{X})^{-1}$の計算に時間がかかる

$\mathbf{X}$は特徴量数$n$,データ数$m$とすると$m\times(n+1)$の行列です．$\mathbf{X}^T$は転置されているので$(n+1)\times m$の行列です．これらの積$\mathbf{X}^T\mathbf{X}$は$(n+1)\times(n+1)$の行列となります．今回は特徴量はcarat一つだったので，2×2の行列でした．

$n$が大きくなると，かなり大きな行列となり，その逆行列を計算するのにとても時間がかかります．$n$が大きい場合(例えば1万とか)は，最急降下法を使って解きましょう！(計算量は$n^3$のペースで増えていきます．)

2.特徴量同士に強い相関があると$(\mathbf{X}^T\mathbf{X})$の逆行列を求めることができない

$
\mathbf{A}=\begin{pmatrix}
a & b \\
c & d \\
\end{pmatrix}
$の逆行列は，$
\mathbf{A}^{-1}=\frac{1}{ad-bc}
\begin{pmatrix}
d & -b \\
-c & a \\
\end{pmatrix}
$で求めることができます．

特徴量同士に完全な相関があるということは上記の行列$\mathbf{A}$は\begin{pmatrix}
a & ca \\
b & cb \\
\end{pmatrix}のようになります．この場合上記の$ad-bc$が0になり，逆行列を求めることができません．

これは$\mathbf{A}^T\mathbf{A}$でも同じようになります．

補足
完全な相関がなかったとしても，相関が強いと$ad-bc$がかなり小さい値になり，逆行列の値のブレが大きくなり結果が不安定になります．一般的に特徴量間に強い相関がある場合は，学習がうまくいかないことが多いので，どちらかの特徴量を落とすなど対策が必要です．これは多重共線性(multicolinearlity)と呼ばれる有名な問題で，よく日本語ではマルチコと称されることが多いです．これについてはまた別の記事で詳しく取り上げます

例えば今回の例ではカラットを特徴量として使いましたが，カラットは質量を表す指標なので，同じように「グラム」という特徴量があると，カラットとグラムでは完全な相関(1カラット=0.2グラム)があるため学習がうまくいかなくなります．ここまで完全な相関じゃなかったとしても，特徴量同士が強い相関を持つことは多いです．注意しましょう！

この場合，どちらかの特徴量を落としたり，それぞれの特徴量を使って新たな特徴量を作ったりすることで回避します．(この辺りは別の記事でまた扱います！)

3.特徴量数(+1)がデータ数を上回る場合，回帰のパラメータを特定できない

極端な例ですが，($\hat{f}(X_1)=\theta_0+\theta_1X_1$)という回帰モデルを作りたい場合(特徴量数は1+1で2としましょう．)

データ数が1つしかないと，以下のようになり，2次元上に回帰直線を定めることができませんね．これは多次元になっても同じです．例えば特徴量数が2+1=3の場合，下図は3次元になり回帰モデルは平面になりますが，もし二つしかデータがない場合は平面を特定できません．

じゃぁどうすればいいの？？

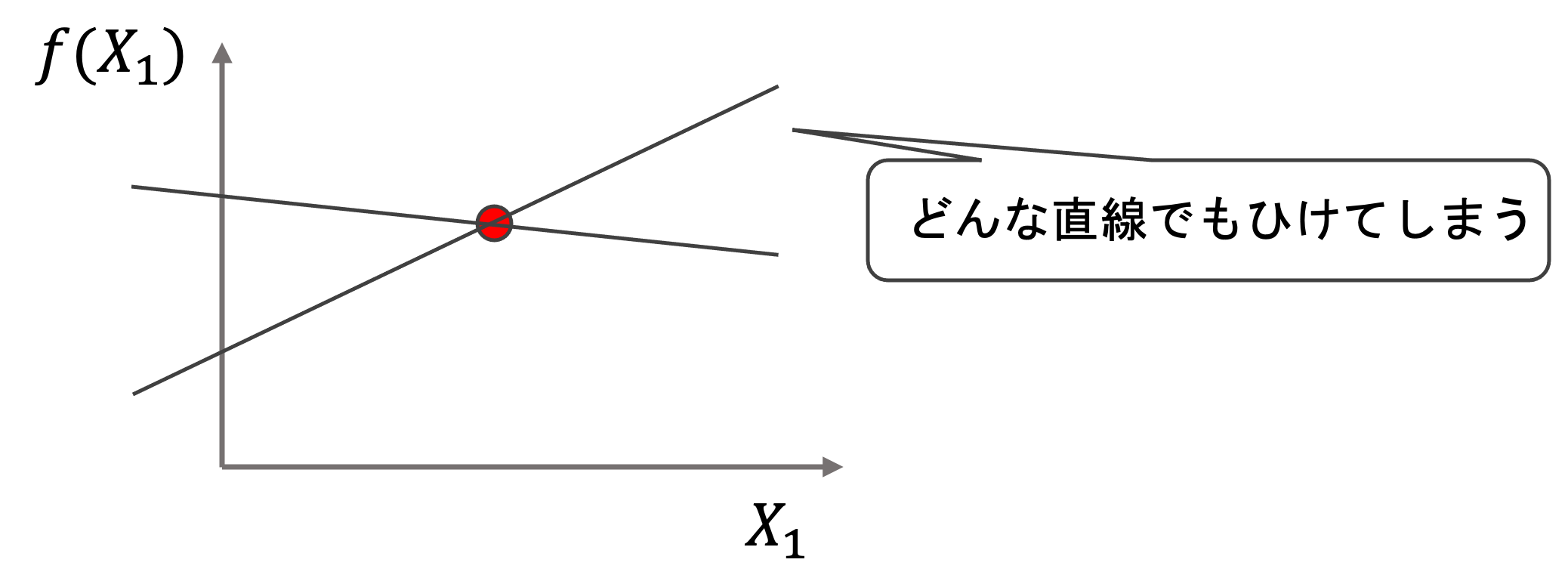
この場合，もっと多くのデータを取ってくるか，特徴量を減らす必要があります．最近では技術の発達によってデータも特徴量もたくさん取ってこれるなんてこともよくあります．そんなときは特徴量をうまく減らしたりして，この問題を避けます．

補足
どの特徴量をモデル構築に使用するかは機械学習において非常に重要な課題です．今後の記事で特徴量選択をするアルゴリズムを扱っていきます．また，特徴量を増やすべきなのかデータを増やすべきなのかの考え方も今後の講座で扱っていく予定です！この辺りは非常に重要な項目なので今後の講座でしっかり学んでいきましょう！

まとめ

かなり長くなってしまいましたが，今回の記事で正規方程式を使って線形回帰のモデルを構築しました．通常線形回帰のモデル構築には正規方程式を使うのが一般的なので，きちんと理解しておきましょう！

正規方程式$\theta=(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y}$により，線形回帰のモデルを構築する
学習データを正規方程式に代入することで解析的に線形回帰のパラメータを求めることができる
特徴量の数が多いと$(\mathbf{X}^T\mathbf{X})^{-1}$を求めるのに時間がかるので，その場合は最急降下法を使う
特徴量同士に強い相関があると$(\mathbf{X}^T\mathbf{X})^{-1}$が計算できないので，どちらかの特徴量を落としたりする必要がある
特徴量数が学習データ数を超えると線形回帰のパラメータが一意に定まらないので，特徴量を減らすなどの工夫が必要

今回はnumpyを駆使してスクラッチで正規方程式を実装してみましたが，次回はscikit-learnという機械学習に特化したPythonのライブラリを使って，もっと簡単に線形回帰のモデルを構築してみたいと思います！　業務で機械学習をする最には基本的にはscikit-learnを使うことになるので，次回の記事はより実践的な内容になります．

それでは！！

追記) 次回の記事書きました！