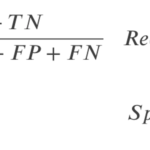データサイエンス入門の機械学習編第21回です.(講座全体の説明と目次はこちら)
追記)機械学習超入門動画講座を公開しました!動画で効率よく学習をしたい人はこちら(現在割引クーポン配布中です)
今回は前回の記事に引き続き分類器に使われる評価指標を紹介していきます!今回紹介するのはF値 (F-score)です.
F1値は分類器を評価する単一の評価指標としてよく使われる指標なのでしっかり覚えておきましょう.(前回紹介した指標群は,単一では使いにくいものでしたね)
また,F値はPrecisionとRecallのトレードオフとも深い関係があります.この辺りは高い精度の分類器を構築する上で必要不可欠な知識になるので非常に重要です.
それではみてみましょう!
目次
F値 (F-score)
F値(F-score)は,RecallとPrecisionの調和平均です.F-measureやF1-scoreとも呼びます.
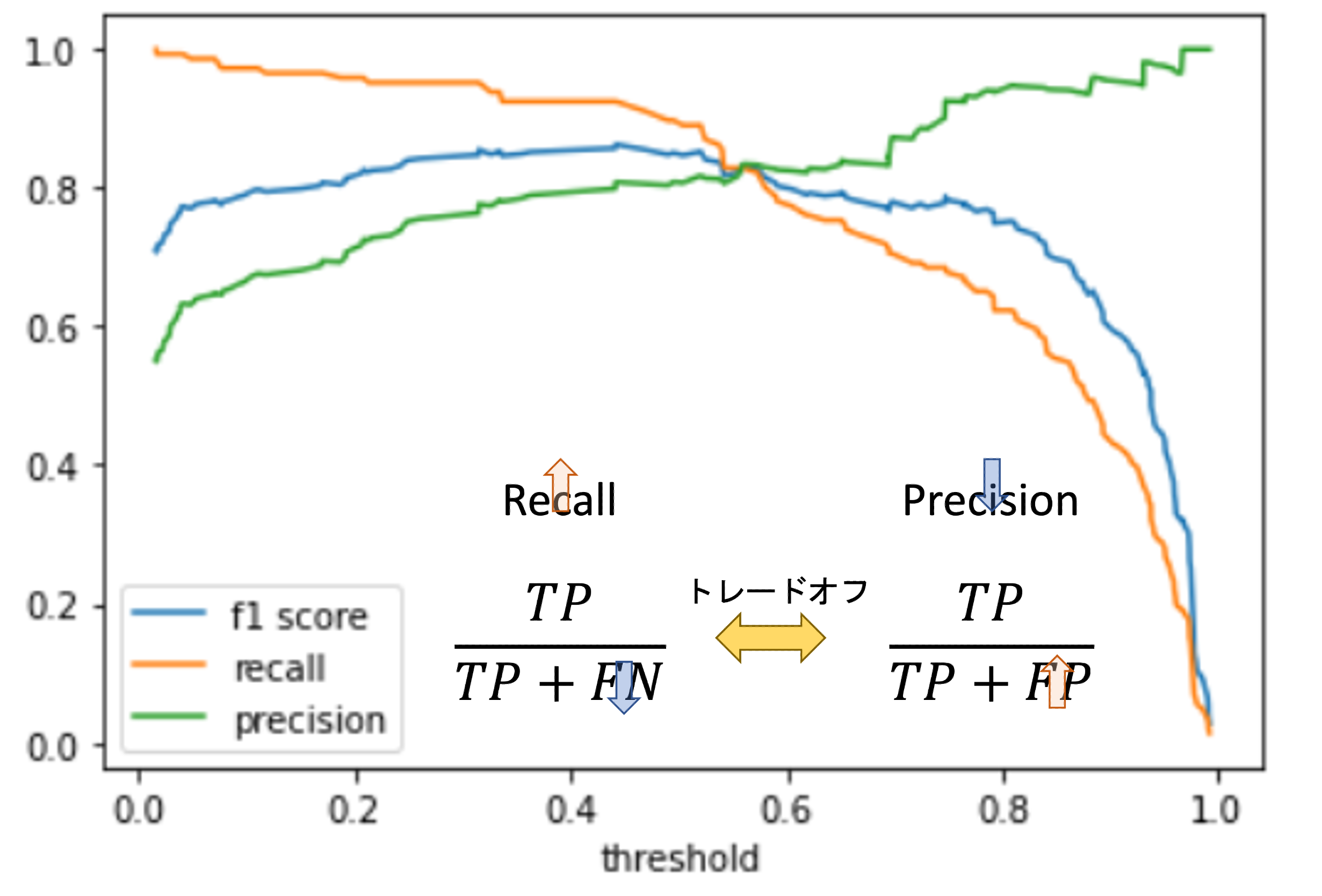
実は,Recall(\(\frac{TP}{TP+FN}\))とPrecision(\(\frac{TP}{TP+FP}\))はトレードオフの関係にあって,片方を高くしようとすると,もう片方が低くなる関係にあります.
例えば,Recallを高くしようとして積極的に”Positive”と予測する場合,本当はPositiveだけどNegativeと誤ってしまう(FN: False Negative)数は下がりRecallは高くなりますが,本当はNegativeなのにPositiveと誤ってしまう(FP: False Positive)数が増えてしまうので,Precisionは下がってしまいます.
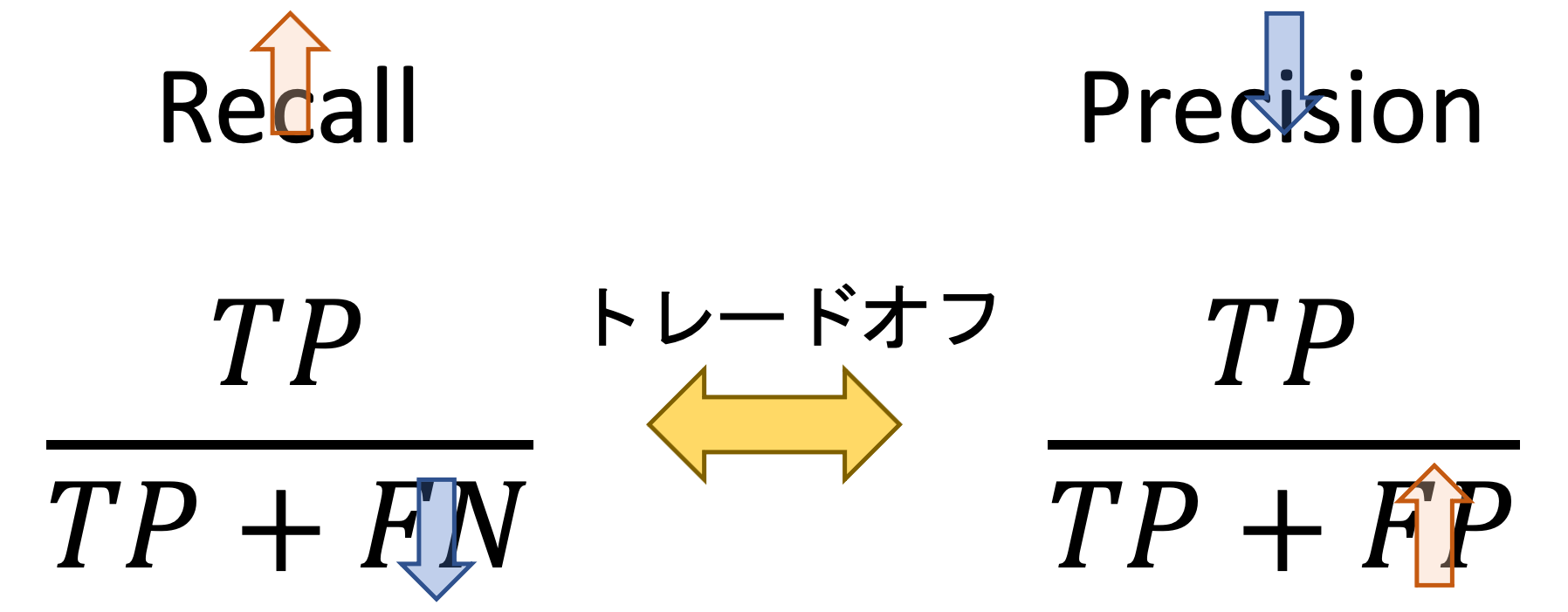
つまり,Recallを高くしようとして誰にでも「あなた病気です!」っていうと,間違えて病気と誤診してしまう数もあがりPrecisionは下がってしまうということです.
なので,RecallやPrecision単体でみても,一概に精度の良し悪しは言えません.そこで出てきたのがF値です.F値はこのトレードオフを考慮して調和平均を取った値なのです
$$\text{F-score}=\frac{2}{\frac{1}{\text{Recall}}+\frac{1}{\text{Precision}}}=\frac{2\times \text{Recall}\times \text{Precision}}{\text{Recall} + \text{Precision}}$$
調和平均がわかってさえいれば,F値の式は難しくないですね.(調和平均について統計学講座第2回を参照ください.)
PythonでF値 (F-score)を計算する
PythonでF値を計算するには, sklearn.metrics.f1_score を使います.こちらも今までのmetrics同様, y_true と y_pred を渡します.また,同様に多クラスの場合は average 引数を渡します.(前回の記事のロジスティック回帰の結果(y_test, y_pred)をそのまま使います.コードを載せると本記事が長くなってしまうので割愛します...)
|
1 2 |
from sklearn.metrics import f1_score f1_score(y_test, y_pred, average='macro') |
|
1 |
0.9511784511784511 |
F値は最終的にモデルを選択する際の評価指標として使われることが多いです.つまり,F値が最も高いモデルを最高精度とするわけですね.
PrecisionとRecallのトレードオフ

という人のために,PrecisionとRecallのトレードオフについて詳しく見てみましょう!
これを確認するには,分類器が出力した確率の閾値を変えるとPrecisionとRecallがどう変わるのかを見ます.
通常の model.predict() では,2値分類では閾値が0.5になっていますね.
閾値が0.5ということは,確率が高い方のラベルが最終的な予測ラベルになるので自然ではあるんですが,これは簡易的であり,実際にはアプリケーションによって適切な閾値を選択する必要があります.(これはまさにRecallを高くしたいのかPrecisionを高くしたいのかによって変わってきます.)
今回は例として,KaggleにあるHeart disease datasetでロジスティック回帰をして,その結果を使ってみます.(Kaggleの登録やデータセットの使用についてはデータサイエンスのためのPython講座第11回を参考にしてください.)
本データセットには,患者の属性や血圧などの値と心臓病かどうかが記されています.データの詳細はKaggleのページを参考にしてください.本記事ではあくまでもPrecisionとRecallのトレードオフに焦点を当てるので,データの中身については割愛します.
データ取得
Kaggleにログイン後,Heart disease datasetのページからheart.csvをダウンロードし,コードからアクセスできるフォルダに入れておきましょう.
|
1 2 3 |
import pandas as pd df = pd.read_csv('heart.csv') df.head() |
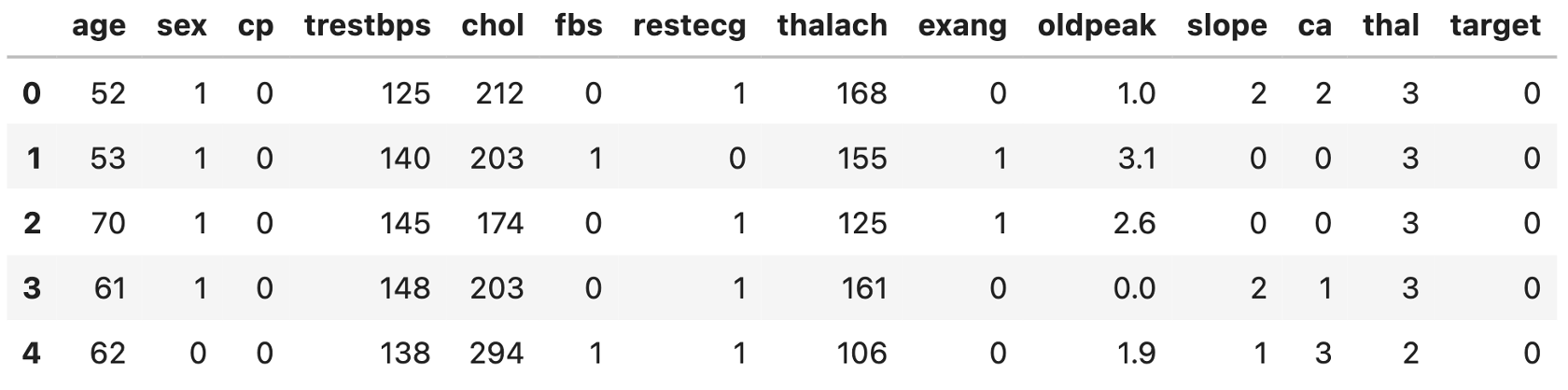
‘target’カラムにその患者が心臓病を患っているかの情報が入っています.(0は陰性,1は陽性ですね.)その他のカラムについてはKaggleのページを参考にしてください.
前処理(preprocessing)
本データセットには質的変数も含まれているので,それらをダミー変数にしたり,無効なレコードを落としたりする必要があります.
これらの前処理(Preprocessing)をやっていきましょう.今回はこちらのKaggleのページを参考に以下の処理をしておきます.(他にもEDAなど色々と参考になる情報が載っているので興味がある人は一読してみるといいと思います!)
今回はあくまでもPrecisionとReallのトレードオフにフォーカスしたいので,あまり解説はしません.コードはコピペしてただ実行するだけでOKです◎
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
# 異常値の削除 df = df[df['ca'] < 4] #drop the wrong ca values df = df[df['thal'] > 0] # drop the wong thal value # カラム名をもっとわかりやすい名前に変換 df = df.rename(columns = {'cp':'chest_pain_type', 'trestbps':'resting_blood_pressure', 'chol': 'cholesterol','fbs': 'fasting_blood_sugar', 'restecg' : 'rest_electrocardiographic', 'thalach': 'max_heart_rate_achieved', 'exang': 'exercise_induced_angina', 'oldpeak': 'st_depression', 'slope': 'st_slope', 'ca':'num_major_vessels', 'thal': 'thalassemia'}, errors="raise") # 質的変数の値がintegerになっているので,文字列にする(ついでにわかりやすい値を入れる df['sex'][df['sex'] == 0] = 'female' df['sex'][df['sex'] == 1] = 'male' df['chest_pain_type'][df['chest_pain_type'] == 0] = 'typical angina' df['chest_pain_type'][df['chest_pain_type'] == 1] = 'atypical angina' df['chest_pain_type'][df['chest_pain_type'] == 2] = 'non-anginal pain' df['chest_pain_type'][df['chest_pain_type'] == 3] = 'asymptomatic' df['fasting_blood_sugar'][df['fasting_blood_sugar'] == 0] = 'lower than 120mg/ml' df['fasting_blood_sugar'][df['fasting_blood_sugar'] == 1] = 'greater than 120mg/ml' df['rest_electrocardiographic'][df['rest_electrocardiographic'] == 0] = 'normal' df['rest_electrocardiographic'][df['rest_electrocardiographic'] == 1] = 'ST-T wave abnormality' df['rest_electrocardiographic'][df['rest_electrocardiographic'] == 2] = 'left ventricular hypertrophy' df['exercise_induced_angina'][df['exercise_induced_angina'] == 0] = 'no' df['exercise_induced_angina'][df['exercise_induced_angina'] == 1] = 'yes' df['st_slope'][df['st_slope'] == 0] = 'upsloping' df['st_slope'][df['st_slope'] == 1] = 'flat' df['st_slope'][df['st_slope'] == 2] = 'downsloping' df['thalassemia'][df['thalassemia'] == 1] = 'fixed defect' df['thalassemia'][df['thalassemia'] == 2] = 'normal' df['thalassemia'][df['thalassemia'] == 3] = 'reversable defect' #質的変数をダミー変数にする df = pd.get_dummies(df, drop_first=True) df.head() |

学習データ作成,学習,予測
それでは,いつも通りロジスティック回帰を実行してみます.今回も学習データとテストデータを7:3に分けて学習させていきます.
デフォルトの solver='lbfgs' では収束しないことがあるようなので, solver='liblinear' を指定しています.こちらも今まで通りなのでコードはコピペで実行してしまって良いと思います◎
|
1 2 3 4 5 6 7 8 9 10 11 12 |
from sklearn.linear_model import LogisticRegression from sklearn.model_selection import train_test_split # 学習データとテストデータ作成 X = df.loc[:, df.columns!='target'] y = df['target'] X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0) # モデル構築 model = LogisticRegression(solver='liblinear') model.fit(X_train, y_train) # 予測(確率) y_pred_proba = model.predict_proba(X_test) |
Precision-Recallカーブ描画
それでは,得られた y_pred_proba をもとに,PrecisionとRecallのトレードオフのカーブを描画してみます.
これは,片方のラベル(今回は陽性とします.)の確率に対しての閾値を変動させた時にPrecisionとRecallがどう変化するかをplotしたものです.
自分で閾値のリストを作って前回の記事で紹介したようにPrecisinとRecallを計算してplotしていってもいいんですが,scikit-learnにはこれを簡単にしてくれる sklearn.metrics.precision_recall_curve という関数が用意されているのでこれを使います.(scikit-learn便利すぎる!!)
precision_recall_curve() には第一引数に正解ラベルのリストである y_true , 第二引数に陽性ラベルの確率のリストである probas_pred を入れます.probas_pred は通常, model.predict_proba() の出力の陽性ラベル側の確率リストになります. model.decision_function() を使うやり方もありますが,本講座では model.decision_function() は割愛します.
そして, precision_recall_curve() はprecision, recall, thresholdのリストをそれぞれ返します.それぞれのthreshold(閾値)に対してのPrecisionとRecallがリストになって返ってくるわけです.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
import matplotlib.pyplot as plt from sklearn.metrics import precision_recall_curve %matplotlib inline # 陽性の確率だけが必要なので[:, 1]をして陰性の確率を落とす pos_prob = model.predict_proba(X_test)[:, 1] precision, recall, thresholds = precision_recall_curve(y_test, pos_prob) # 描画a plt.plot(recall,precision) plt.xlabel('Recall') plt.ylabel('Precision') plt.title('Precision Recall Curve') plt.show() |
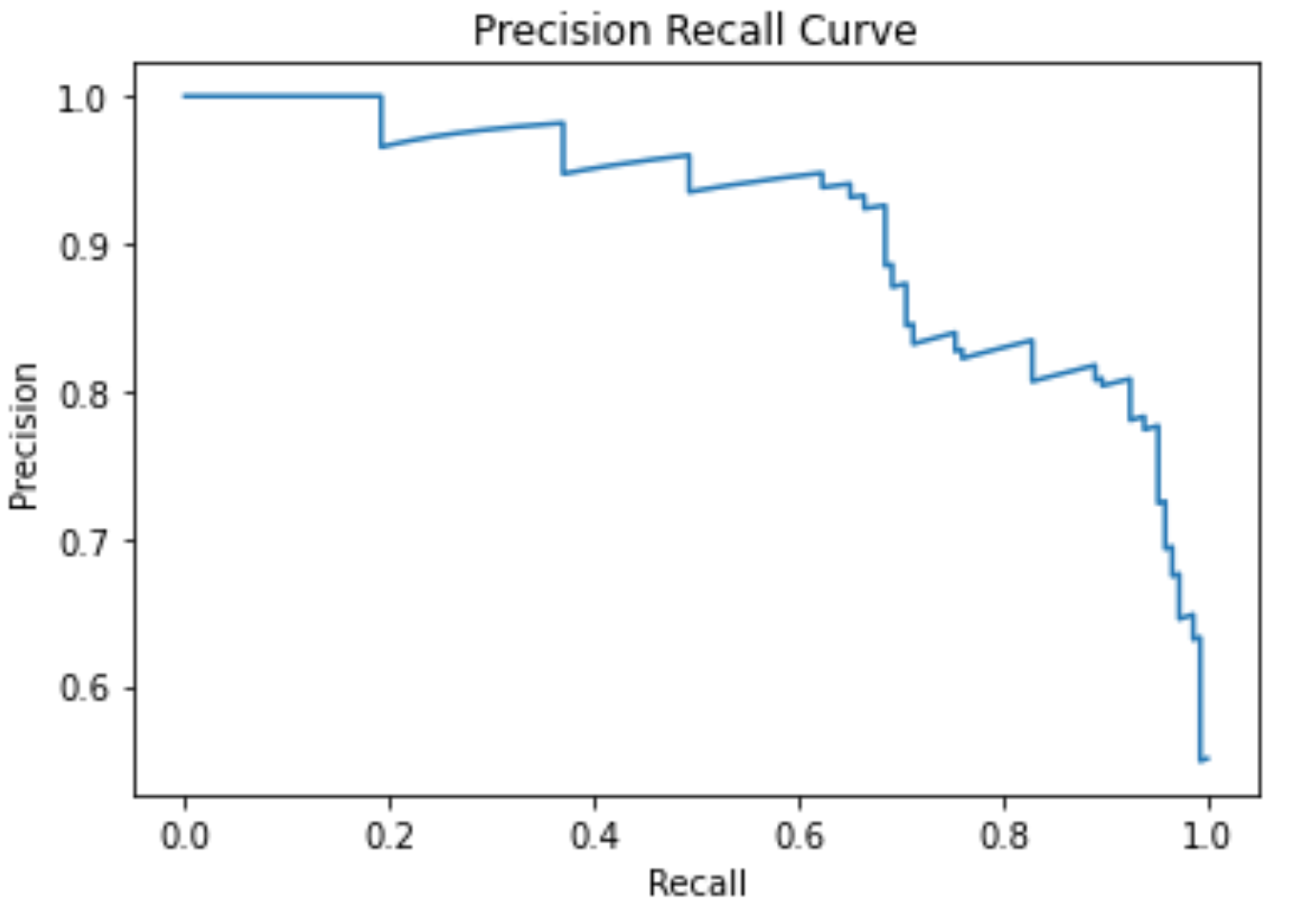
これがPrecisionとRecallのカーブです.例えば陽性の閾値が0だった場合,全てのデータに対して陽性と予測することになるので,\(Recall=\frac{TP}{TP+FN}\)は1になりますが,\(Precision=\frac{TP}{TP+FP}\)は最も低い値になります(FPが最大になるため).
一方閾値が上がっていくと,陰性と予測するデータが増えていくため,FN(False Negative)が増え,FP(False Positive)が減っていくので,Recallが低くなる一方Precisionは高くなっていきます.
そして閾値が1になると,全てのデータに対して陰性と予測することになるので,一つも陽性データに対して正しく陽性と予測できずRecallは0となり,Precisionはそもそもどのデータに対しても陽性と予測しなくなるので1になります.

これはアプリケーションによります.例えば今回のような病気の陽性/陰性を予測するアプリケーションを考えるのであれば,偽陰性(本当は陽性なのに陰性と予測してしまう)はなるべく避けたいですよね?本当は心臓に病気がある人を見逃すことになってしまうので.
なのでこの場合はRecallが高くなるように閾値を下げ,多くのデータに対して陽性と予測するようなモデルが必要になってきます.
PrecisionとRecallとF値の関係
PrecisionとRecallをどちらもいい具合(”平均的”)に高くなるような閾値を選択したい時は,F値が最も高くなる閾値を選ぶのが一般的です.
先ほどの各閾値に対してのPrecisionとRecallからF値を求めてみましょう.F値はPrecisionとRecallの調和平均(harmonic mean)をとればいいので, numpy.hmean() を使って計算していけばOKです.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
import numpy as np from scipy.stats import hmean # F値計算 f1_scores = [] for p, r in zip(precision, recall): f1 = hmean([p, r]) f1_scores.append(f1) # Precision, Recall, F値を描画(vs 閾値) plt.plot(thresholds, f1_scores[:-1], label='f1 score') plt.plot(thresholds, recall[:-1], label='recall') plt.plot(thresholds, precision[:-1], label='precision') plt.xlabel('threshold') plt.legend() print(f'{np.argmax(f1_scores)}th threshold(={thresholds[np.argmax(f1_scores)]:.2f}) is highest f1 score ={np.max(f1_scores):.2f}') |
|
1 |
66th threshold(=0.44) is highest f1 score =0.86 |
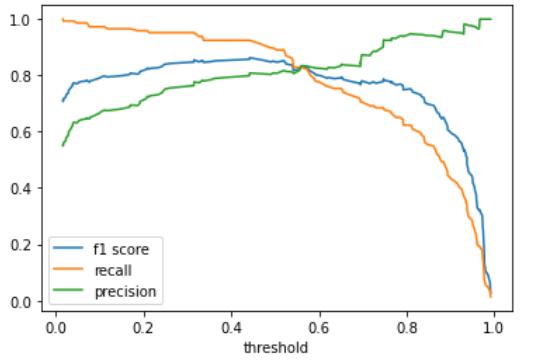
この図をみると,それぞれのPrecisionとRecallに対してF値がどのように変化しているかがわかります.
F値の式(\(\frac{2\times Recall\times Precision}{Recall + Precision}\))を見てわかるように,分子にはRecallとPrecisionの掛け算がきています.つまり,片方の値が極端に低い場合,どんなにもう片方の値が高くてもF値は低くなります.これは調和平均の特徴であり,単純に算術平均をとってもこうはなりません.
F値が最も高いのは閾値が0.44の時で,図を見てもわかるように,RecallもPrecisionもどちらもある程度高くなっていますね!
普通にロジスティック回帰を構築して model.predict() をすると閾値が0.5の場合での予測になってしまうんですが,このようにF値がもっとも高くなるような閾値を探すことでより精度の高いモデルを作ることができます.(必ずしも0.5が最良の閾値とは限らないわけです.)
また,アプリケーションによってはもう少しRecallを高くしたり,逆にPrecisionを高くしたりして調整することもできます.
なので,基本的に分類器を構築する時は単純に model.predict() を使ってラベルを予測するのではなくて, model.predict_proba() で確率の値を得て,適切な閾値を模索することになります.
必要な精度指標がちゃんとわかれば,それに応じて高い精度のモデルを構築することができるわけで,そのためにもちゃんと精度指標を理解し,適切な指標を選択できる必要があります.
まとめ
少し長くなってしまいましたがまとめです.今回はF値と,PrecisionとRecallのトレードオフについて紹介しました.
- F値(F-score)は,RecallとPrecisionの調和平均で\(\frac{2\times Recall\times Precision}{Recall + Precision}\)で計算される値
- RecallとPrecisionはトレードオフの関係にあり,予測結果の確率に対しての閾値を変更し片方を高くしようとするともう片方が低くなってしまう
- 閾値は必ずしも0.5が最適とは限らず,どこに設定するかはアプリケーション次第
- RecallもPrecisionもどちらも重要な場合はF値が最大となるように閾値を設定する
F値は分類器のモデル構築では本当によく使われる指標なので,今回の記事の内容をしっかりと頭に入れておきましょう!
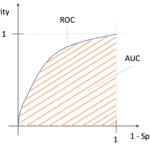
次回の記事では,ROCカーブとAUCという非常に重要な評価指標を紹介します!これはRecall(Sensitivity)とSpecificityのトレードオフに関係してきます.
ROCカーブの知識なしで分類器を構築することはほぼ不可能と言えるくらい超重要事項です.しっかり学んでいきましょう!
それでは!
追記)次回の記事書きました.超重要事項です!