データサイエンス入門の機械学習編第18回です.(講座全体の説明と目次はこちら)
追記)機械学習超入門動画講座を公開しました!動画で効率よく学習をしたい人はこちら(現在割引クーポン配布中です)
前々回の記事と前回の記事でロジスティック回帰の理論の話をしましたが,今回の記事では実際にデータに対してPythonでロジスティック回帰を使って分類器を作るやり方を紹介します.
基本的な流れは今までの他の機械学習モデルと同じようにすればOKです.
それではやっていきましょう〜
データ準備
今回のデータは分類タスクのサンプルデータで有名なirisデータセットを使っていきます.今までの記事同様,seabornのload_dataset関数を使います.
|
1 2 3 |
import seaborn as sns df = sns.load_dataset('iris') df.head() |
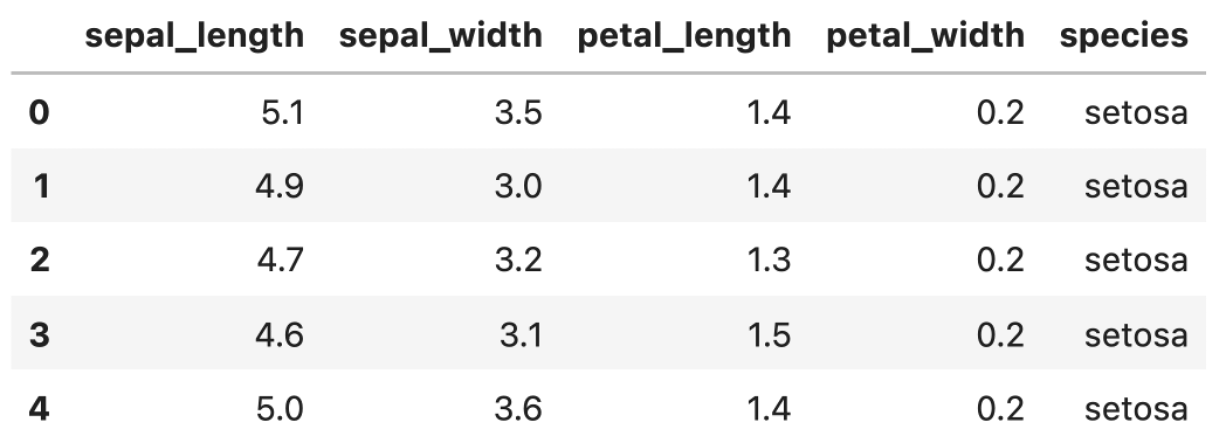
irisはアヤメという花の名前で,本データセットはsetosa(ヒオウギアヤメ), versicolor(ブルーフラッグ), virginica(日本語訳不明)という3つの種( species )のそれぞれの以下の4つの特徴量の値を記載しています.
- sepal_length : がく片の長さ
- sepal_width : がく片の幅
- petal_length : 花びらの長さ
- petal_width : 花びらの幅
この4つの値から,あやめの種をうまく分類する分類器を作ることを考えます,
興味がある人はデータセットについて色々と調べてみてください.今回は詳細は割愛し,sns.pairplotで概要だけ掴みましょう.
|
1 |
sns.pairplot(df, hue='species') |
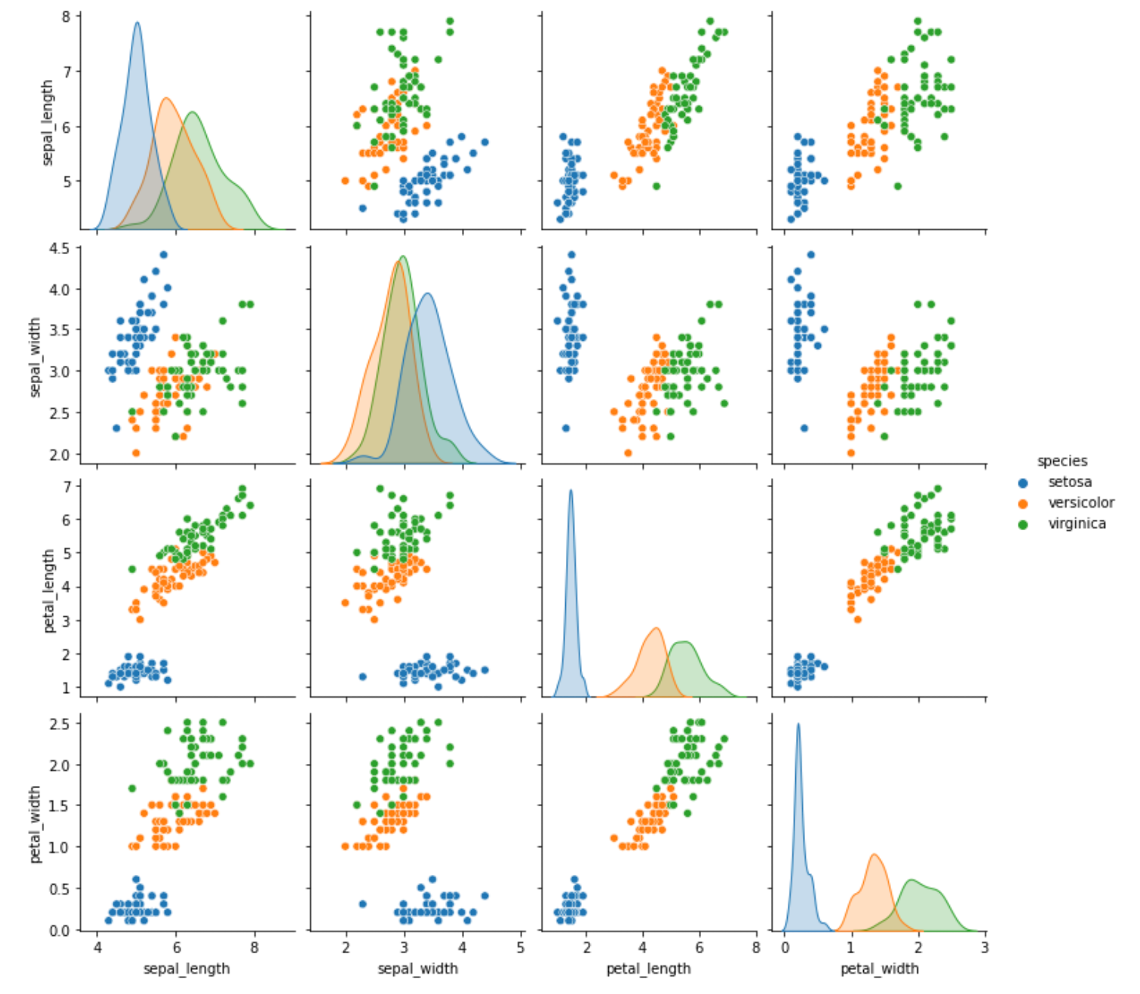
各 species で色分けしてみました.結構綺麗に分かれてそうですね.今回のデータセットに入っている4つの特徴量をみるだけで,これらの種をそこそこの精度で分類することができそうです.
学習データとテストデータ準備
それではまずは今まで通り学習データとテストデータを作ります.今回はhold-outで7:3にデータを分割します.
|
1 2 3 4 5 |
from sklearn.model_selection import train_test_split X = df.loc[:, df.columns!='species'] y = df['species'] X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0) print(len(X_train), len(X_test)) |
|
1 |
105 45 |
すると,学習データ105個,テストデータ45個に分割できました.
それではこの学習データに対してロジスティック回帰で分類器モデルを作ってみましょう!
学習
ロジスティック回帰は sklearn.linear_model.LogisticRegression を使います.

ロジスティック回帰は,実際にやっていることは線形回帰をして,最後にシグモイド関数を使って出力を0~1に収めているので,実は線形モデルの仲間なんです.なので LinearRegression クラス同様, sklearn.linear_model の中に入ってます!
LogisticRegression クラスはインスタンス生成時に様々な引数を取ります.全部理解する必要はないのですが,重要な引数を以下に書いておきます.- penalty : 正則化項を選択します.以下の4つの文字列から選択します.デフォルトは”l2″が設定されています.
-
solver : 最適化アルゴリズムを選択します.以下の5つの文字列から選択します.各アルゴリズムの詳細は本講座では対象外です.デフォルトはバージョン0.0.2以降は
"lbfgs" が設定されています.それ以前は
"liblinear" が設定されています.以下に簡単にそれぞれの特徴だけ記しておきます.
- 'newton-cg' : 2次微分を使って最適化をしていきます.2次微分を使うので計算量がかなり高いです.
- 'lbfgs' : 2次微分を近似するBFGS法のLimited-memory版.限られたメモリで実行できるようにしたもので,よく使われます.小さいデータセットでは比較的いい精度がでます.
- 'liblinear' : 特徴量が高次の場合に推奨されます.多クラス分類の場合“One-vs-Rest”となります.
- 'sag' : Stochastic Average Gradientの略です.データ数や特徴量数が大きい場合,他のアルゴリズムより早く収束します.
- 'saga' : SAGアルゴリズムの仲間で,L1ノルムの正則化項に対応したバージョンです.
- random_state : solver が 'sag' , 'saga' , 'liblinear' の場合,データがシャッフルされるので,その際の乱数の種を指定します.
- multi_class : 多クラス分類の場合, 'ovr' , 'auto' , 'multinomial' から選択します.デフォルトは 'auto' で,この場合solver=’liblinear’の場合だったり2クラス分類の場合は 'ovr' になり,それ以外では 'multinomial' (多項ロジスティック回帰)になります.
少し厄介なのが, solver の値によって,サポートしている penalty と multi_class が異なります.scikit-learn公式ドキュメントにまとめ表があるので貼っておきます.
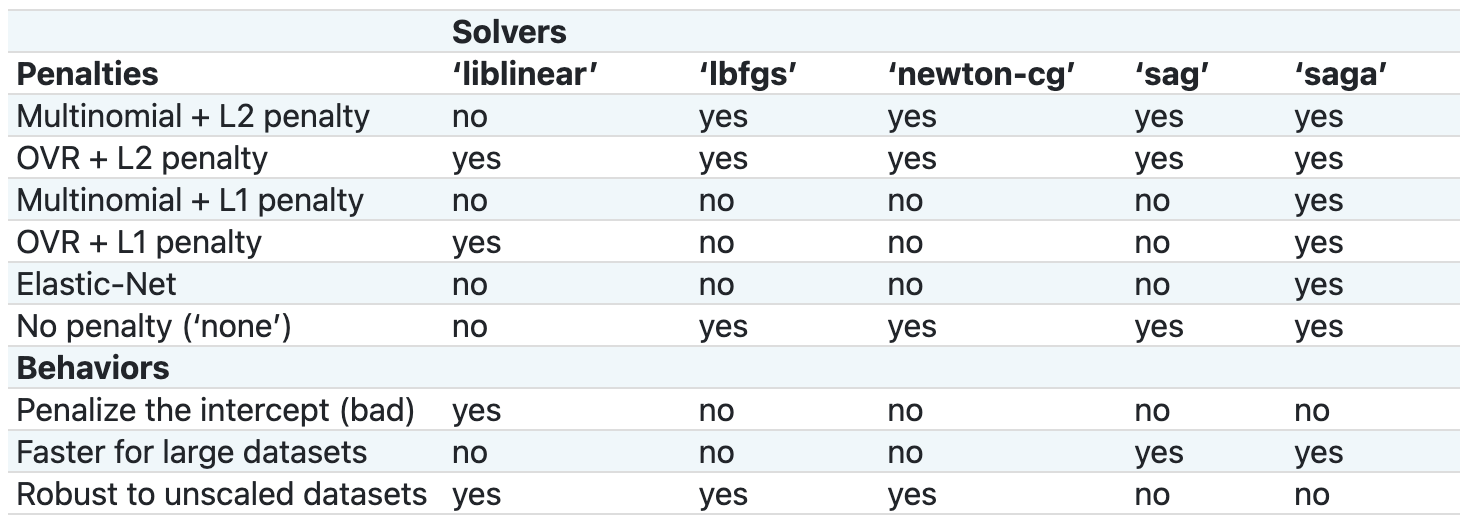

この辺りを100%理解して最適なパラメータを選択するのは難しいです.なので,まずはそれぞれのパラメータの組み合わせでモデルを作って,k-foldCVなどで汎化性能を測定して,最も精度が高いものを選ぶのでいいでしょう.余裕があればこの表を見てから組み合わせを作るといいと思います.)
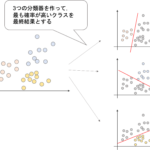
また,多クラス分類の場合はMultinomial lossを使う場合とOVR(One-vs-Rest)を使う場合の二種類があります.これについては前回の記事で解説した通りです.
色々書きましたが,今回は solver はデフォルトの 'lbfgs' で正則化項は無し( penalty='none' )を指定してやってみましょう!
|
1 2 3 |
from sklearn.linear_model import LogisticRegression model = LogisticRegression(penalty='none') model.fit(X_train, y_train) |
こんな感じでいつも通り簡単にモデルを学習させることができます♪
今回は特徴量の標準化を行いませんでしたが,特徴量のスケールが違いすぎる場合は標準化をすることで最適化問題の収束が早くなり,学習も安定します.
予測
それでは,学習したモデルを使って,予測してみましょう.
予測をするには回帰モデル同様 .predict() メソッドを呼べばOKです. X_test を引数に渡して予測の結果を見てみましょう.
|
1 |
X_test.head() |
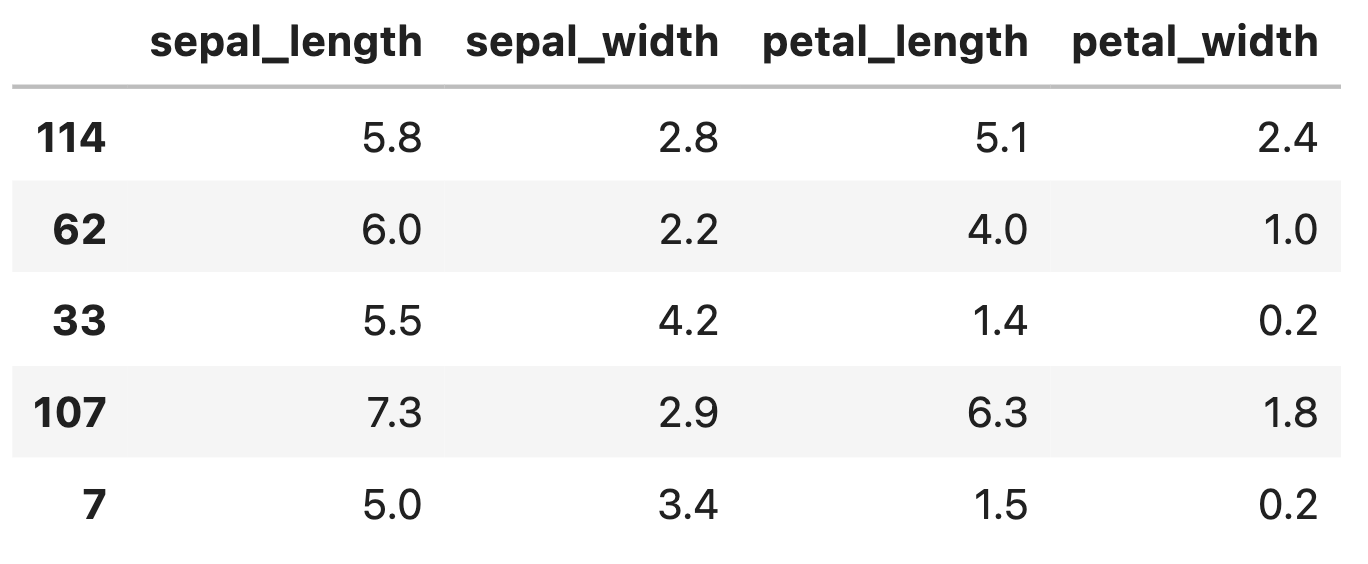
|
1 |
model.predict(X_test) |

すると,それぞれのテストデータの4つの特徴量の値に応じて 'virginica' , 'versicolor' , 'setosa' の3種に分類しているのがわかると思います.
実際に分類器を業務等で使う場合は,それぞれのラベル(クラス)の確率を知りたいケースが多いです.
その場合は .predict_proba() メソッドを使います.使い方は同じです.
|
1 |
model.predict_proba(X_test) |
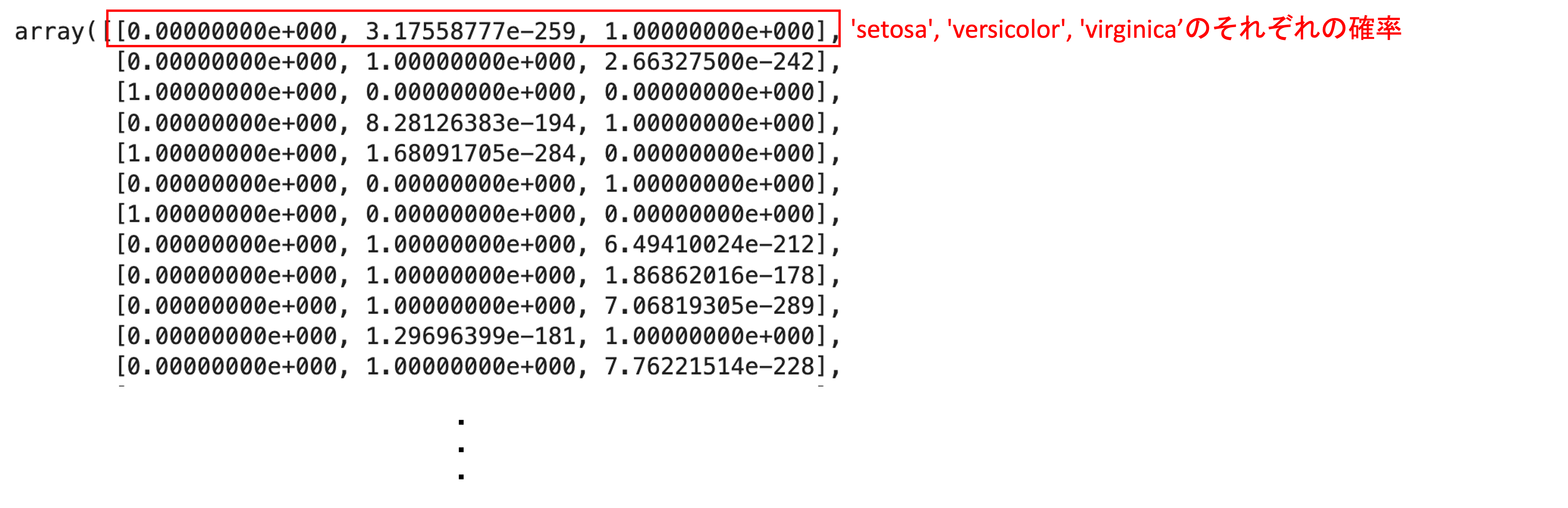
出力の結果は,それぞれのデータに対して,各クラスの確率(=モデルの自信度)がリストで返ってきます.例えば一つ目のデータの場合,’setosa’の確率が0で’versicolor’の確率が3.17×10^-259とほぼ0で,’virginica’の確率が1です.つまり結果は’virginica’ということですね.
ちなみにクラスの順番は model.classes_ の順です.
|
1 |
model.classes_ |
|
1 |
array(['setosa', 'versicolor', 'virginica'], dtype=object) |
今回のデータセットは先ほど見た通り,かなり簡単に分類できるデータなのでどの結果を見てもほぼほぼ確率100%で分類しています.
モデルの係数を確認
それでは学習したモデルがどのような形になっているのか見てみましょう!
今回は 'multi_class'='auto' で solver='lbfgs' なので多項ロジスティック回帰になります.
多項ロジスティック回帰の式はソフトマックス関数を使った以下の式です.
$$p_k(x)=\frac{e^{\theta^k_0+\theta_1^kX_1+\theta_2^kX_2+\theta_3^kX_3+\theta_4^kX_4}}{\sum_{i=1}^{3}e^{\theta^k_0+\theta_1^kX_1+\theta_2^kX_2+\theta_3^kX_3+\theta_4^kX_4}}$$
\(\theta^k_0\)(\(k=1, 2, 3\))は model.intercept_ で,\(\theta^k_i\)(\(k=1, 2, 3 i=1, 2, 3, 4\))は model.coef_ でアクセスすることができます.
これも LinearRegressionクラスと同じですね!
|
1 |
model.intercept_ |
|
1 |
array([ 80.23761444, 129.79120181, -210.02881625]) |
|
1 |
model.coef_ |
|
1 2 3 |
array([[ 155.59730304, 358.73831715, -523.93810374, -248.11591547], [ 118.20298173, -15.08081916, -41.54669791, -91.11018039], [-273.80028477, -343.65749799, 565.48480166, 339.22609586]]) |
\(k\)の順番は先程述べたように model.classes_ です.\(i\)の順番は model.feature_names_in_ の通りです.( .feature_names_in_ はversion 1.0以降で利用可能です.versionが古い人は $pip install --upgrade scikit-learn で更新しましょう.Jupyter noteで実行する場合は ! をつけてください.)
|
1 |
model.feature_names_in_ |
|
1 2 |
array(['sepal_length', 'sepal_width', 'petal_length', 'petal_width'], dtype=object) |
モデルの評価

分類器の精度の指標については,次回の記事以降で紹介していきます!最終的なラベル付け(予測の結果のクラス)をどうするかというのも,この精度の指標に大きく関わってきます.
例えばAというクラスの確率が40%, Bというクラスという確率が60%という結果だった場合,本当にBという結果に分類していいのでしょうか?
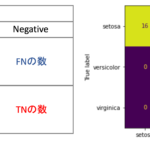
これがもし,病気の陰性/陽性を判定するモデルだったらどうでしょう?陽性の確率40%, 陰性の確率60%だった場合,陰性と結論づけていいのでしょうか?陽性を陰性と間違えて分類することは,陰性を陽性と間違えて分類するよりも問題が大きそうです.(本当は病気なのに病気じゃないって誤診することになるわけなので・・・)
分類器の評価の指標を学習することは,機械学習で分類をする上で必要不可欠です.機械学習の一大分野とも言える内容になってくるので,次の記事でしっかり学んでいきましょう!
まとめ
今回の記事ではPythonでロジスティック回帰のモデルを構築するやり方を紹介しました.他のアルゴリズム同様,scikit-learnを使えば簡単にロジスティック回帰を使うことができます.
- ロジスティック回帰は sklearn.linear_model.LogisticRegression クラスを使う
- インスタンス生成時の引数で, penalty と solver はそれぞれ組み合わせがあることに注意する.
- .predict_proba() で引数のデータの分類の結果を確率で返す. .predict() では最も高い確率のクラスの結果を返す.
次回の記事以降では分類器の評価指標について紹介していきます!モデルを学習して終わりなんてことはなく,必ずモデルの評価が必要になります.
分類器を正しく評価するためにはケースに応じて正しい評価指標を使う必要があります.引き続き学んでいきましょう!!
それでは!