データサイエンス入門の機械学習編第14回です.(講座全体の説明と目次はこちら)
追記)機械学習超入門動画講座を公開しました!動画で効率よく学習をしたい人はこちら(現在割引クーポン配布中です)
今回の記事では,正則化項というものを用いてアルゴリズムが自動で特徴量選択をするLassoという機械学習のアルゴリズムを紹介します.
Lassoは非常に有名なアルゴリズムで,多くの場合普通の線形回帰をするよりもこのLassoを使うのが一般的と言えるくらい重要なアルゴリズムです.
適切に特徴量を選択できるスキルは機械学習において非常に重要なので今回の記事できちんとアルゴリズムを理解し使えるようにしましょう!
目次
特徴量選択
最近ではコンピュータの高性能化やセンサーの多様化などによって本当に多くのデータを取得して管理するのが当たり前になってきて,特徴量を取得できるようになりました.これはモデル精度向上の観点では◎かもしれませんが,特徴量間の相関が強かったり目的変数と全く関係のない特徴量がノイズとして存在してしまったりと,闇雲に全ての特徴量を使ってモデル構築するのは危険なんです.
特徴量が多ければ多いほどコンピュータリソースが必要になってきますし,追加のデータを取るにもコストがかかってきます.
特徴量の数がデータの数を上回る場合モデルを構築できないというのは第4回でも言及しました.
特徴量の数の方がデータ数よりも少ないとしても,データの数がそこまで大くない場合はhigh varianceとなってやはり精度が下がる場合があります.
特徴量を減らすことにより劇的に精度が高くなることもあるのと,特徴量が少ない方がやはり解釈がしやすくなります.
以上のことから「不要な特徴量は削除する」というのが機械学習では一般的なアプローチなんです.
正則化項とは
今回紹介するやり方は,アルゴリズムが自動で特徴量選択をしてくれるという非常に便利で優れたやり方です.
これをやってくれるのが,正則化項(regularization term)です.

Step By Stepに解説していくので安心してください!
機械学習の基本は「損失」を最小にするようにモデルのパラメータを学習するんでしたね.「損失」には色々な指標がありますが,第2回で紹介したMSEや第8回のRSSなんかをよく使います.
今回はRSSを損失関数としてみてみましょう!(ただし今回のモデルは線形回帰です)
$$RSS=\sum_{i=1}^{m}{(y_i-\hat{y_i})^2}=\sum_{i=1}^{m}\left(
y_i-\theta_0-\sum_{j=1}^{n}\theta_jx_{ij}\right)^2$$
ただしデータの数を\(m\), 特徴量の数を\(n\)としています.これが最小になるように\(\theta_0,\theta_1,\cdots, \theta_n\)を学習するんでした.
これを最小二乗法と呼ぶんでしたが,Lassoはこれに正則化項というのを追加します.
$$\sum_{i=1}^{m}\left(y_i-\theta_0-\sum_{j=1}^{n}\theta_jx_{ij}\right)^2+\lambda\sum_{j=1}^{n}|\theta_j|=RSS+\lambda\sum_{j=1}^{n}|\theta_j|$$
また,\(\lambda\)は正則化項におけるパラメータです(後程説明)
\(\lambda\sum_{j=1}^{n}|\theta_j|\)は正則化項(regularization term)と呼ばれる項です.
Lassoではこの式を損失関数として学習していきます.
式だけみても「???」だと思うので,これがどういう役割をするかみてみましょう!
切片である\(\theta_0\)は正則化項に入らないことに注意しましょう!
正則化項の役割
通常の最小二乗法ではRSSを最小にするように学習を進めていきますが,Lassoの場合は正則化項\(\lambda\sum_{j=1}^{n}|\theta_j|\)も追加する形で学習を進めます.
これは,係数の値が大きいと損失が大きくなることを意味しているのがわかると思います.
つまり,RSSに追加で課されたペナルティのように考えてください.
RSSのみならず,係数の値\(\theta_j\)も小さくする必要がでてくるということですね.
\(\lambda\)が大きければその影響が大きくなり,モデルはなるべく係数の値を小さくしていきます.

実はこれ,\(\lambda\)を徐々に大きくしていくと,やがて不要な特徴量の係数\(\theta_j\)は0になるんです!
その係数が0ということはその特徴量はモデルには使わないことになるので,不要な特徴量を落とすことにつながるんですね.
実際にPythonでLassoを使ってみる
それでは実際にPythonでLassoのモデルを作ってみましょう.\(\lambda\)を変えるとそれぞれの係数がどう変化するのかもみてみましょう.
sckit-learnでLassoを使うには sklearn.linear.model.Lasso を使います.
Lassoクラスは,インスタンス生成時に引数 alpha に上述した\(\lambda\)をパラメータとして入れます. alpha に0を入れると普通の線形回帰になりますが,その場合は計算量の観点から Lasso クラスではなく LinearRegression クラスを使う方がいいです.
それでは,早速コードを書いてみましょう!
1. データ取得
今回は,ISLRの”Hitters”データセットを使ってやってみたいと思います.公式ドキュメントはこちら.
csv形式のデータセットはhttps://raw.githubusercontent.com/kirenz/datasets/master/Hitters.csvのリンクから取得できます.これをそのままpd.read_csv()に入れてあげればOKです.
|
1 2 3 4 |
import pandas as pd # データ取得 df = pd.read_csv("https://raw.githubusercontent.com/kirenz/datasets/master/Hitters.csv") df.head() |

Hittersデータセットは,1986年と1987年のメジャーリーグの野球選手の成績データと年俸を表しています.Salaryカラムに年俸が記載されていて,単位は$kです.
少し古いデータですが,どういう選手がどれくらい稼いでいるのか興味がある人もいるんじゃないでしょうか?興味がある人は色々とみてみると面白いと思います.(今回はLassoの実装例として使うだけなので,データの詳しい解説は割愛します.)
今回は,他のカラムを特徴量としてSalaryを予測するモデルを構築していきます.
2. 欠損値対応
データにちょくちょく欠損値があるので,今回はシンプルにNaNを含むレコードを全て落とします.
|
1 2 |
# 欠損値対応 df.dropna(inplace=True) |
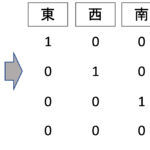
3. ダミー変数作成(one-hot エンコーディング)
本データにはいくつか質的変数があるので,one-hotエンコーディングでダミー変数を作ります.多重共線性(multicollinearity)によるダミー変数トラップを回避するために drop_first=True を指定します.
|
1 2 3 |
# ダミー変数作成 df = pd.get_dummies(df, drop_first=True) df.head() |

4. 学習データとテストデータ作成
|
1 2 3 4 5 6 7 8 9 10 |
from sklearn.model_selection import train_test_split # 目的変数 target = "Salary" # Xは目的変数以外全て X = df.loc[:, df.columns!=target] # yは目的変数のみ y = df[target] # hold-out X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0) |
5. 標準化
Lassoは,それぞれの係数の尺度が異なると,その多きさに引きづられてうまく動作しなくなります.
例えば,元の特徴量の値の尺度が小さすぎて結果係数が大きいものと,そうでないものとでは,正則化項\(\lambda\sum_{j=1}^{n}|\theta_j|\)が与えるインパクトが変わってきますが,これは本来の「特徴量の重要性」とは関係がありません.(このように,特徴量の尺度による多きさのことをマグニチュード(magnitude)と言ったりします.)
そのため,Lassoを使う場合は事前にデータを標準化(平均0,標準偏差1)します.標準化と StandardScaler クラスについては統計学講座第9回で解説をしているのでそちらを参考にしてください!
|
1 2 3 4 5 |
# 標準化 from sklearn.preprocessing import StandardScaler scaler = StandardScaler().fit(X_train) X_train = scaler.transform(X_train) X_test = scaler.transform(X_test) |
標準化の式は\(z=\frac{x-\bar{x}}{s}\)でしたね.\(\bar{x}\)は平均,\(s\)は標準偏差です.
学習時にデータを標準化している場合,予測時にも入力データを同じように標準化する必要があります.(これは前処理とかも同じです.)
ここで注意する点として,学習データに対して平均0, 標準偏差1にした時に使った平均値\(\bar{x}\)と標準偏差\(s\)を使ってテストデータを標準化(上記の\(z\)を求める)する必要があるということ.
テストデータはテストデータで平均0, 標準偏差1にするわけではなく,あくまでも学習データの平均値\(\bar{x}\)と標準偏差\(s\)を使って\(z=\frac{x-\bar{x}}{s}\)を計算します.
なので,コードも .fit() を行うのはあくまでも学習データに対してのみです.この辺りは初学者の人が間違えやすいポイントなので注意しましょう!
ダミー変数に対しても標準化を行うかはよく議論されますが,本講座では基本的に「精度が高ければOK」というスタンスを取ります.ダミー変数に対して標準化をするかどうかは,最終的にどちらの精度が高いかで判断すればいいでしょう.今回の記事ではダミー変数も標準化します
6. 学習,予測,評価
あとは今まで通り,学習してテストデータの予測と,その結果のMSEを計算します.
|
1 2 3 4 5 6 7 8 9 |
from sklearn.linear_model import Lasso model = Lasso() # 学習 model.fit(X_train, y_train) # 予測 y_pred = model.predict(X_test) # 評価 mse = mean_squared_error(y_test, y_pred) print(mse) |
|
1 |
117704.4033881705 |
Lassoクラスの alpha 引数のデフォルトは1です.今回は特に指定せずデフォルトの値を使いました.
7. 係数の確認
LinearRegression 同様, .coef_ で各係数の値を確認することができます.|
1 |
model.coef_ |
|
1 2 3 4 5 |
array([-263.93021843, 267.26811881, 42.953601 , -33.47452958, 7.47725776, 125.12341811, -29.67148909, -238.55413784, 329.80466506, -3.98547868, 259.40614775, 0. , -161.2607052 , 71.00768965, 40.39356866, -30.35965777, -0. , -47.8140956 , 13.94948672]) |
\(\lambda\)によって係数がどう変化するのかみてみる
Lassoを使う場合,\(\lambda\)は非常に重要なファクターです.
\(\lambda\)の値を色々変えると,それぞれの係数がどう変化するのかみてみましょう.
今回は\(\lambda\)の値(コードでは alpha の値)をnp.linspace()を使って,様々な値のリストを作ってfor文で回してみます.
(先ほど作った変数をこちらのコードで使いまわしているのことに注意してください.)
|
1 2 3 4 5 6 7 8 9 10 11 |
from sklearn.metrics import mean_squared_error mse_list = [] coefs = [] alphas = np.linspace(0.01,300,100) for alpha in alphas: model = Lasso(alpha=alpha) model.fit(X_train, y_train) y_pred = model.predict(X_test) mse = mean_squared_error(y_test, y_pred) mse_list.append(mse) coefs.append(model.coef_) |
alpha の値に応じてLassoを構築して,その係数と評価の結果をリストで保存しています.
それでは,各 alpha (\(\lambda\))に対する係数の推移をみてみましょう!
|
1 2 3 4 5 6 |
import matplotlib.pyplot as plt plt.plot(alphas, coefs) plt.xscale('log') plt.xlabel('lambda') plt.ylabel('standardized coefficients') plt.show() |
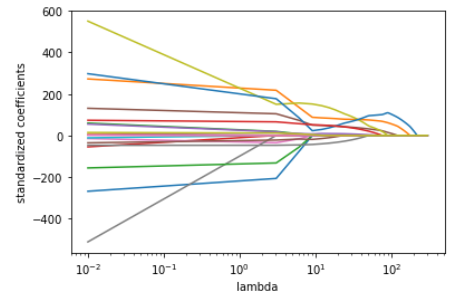
\(\lambda\)を上げていくにつれ,それぞれの係数が小さくなり0になっていっているのがわかると思います.

どの\(\lambda\)を使うべきかは,\(\lambda\)毎のtest errorを計算して最も低いものを選ぶのがいいでしょう.
これをやる場合は,さきのコードのようなhold-outではなくk-fold CVを使ってやるのがいいです.
興味がある人は同じように alpha のリストを作ってforを回してtest errorが一番低くなる alpha (\(\lambda\))を探してみてください!
追記)機械学習超入門動画講座では,Lassoの他にもRidgeというもう一つの正則化項についてもやります.また,これらの正則化項のもう一つの側面からみた数式・考え方についても踏み込んで解説をしているので是非受講ください!(↓の記事に割引クーポンあります)
まとめ
今回の記事では特徴量選定によく使われるLassoというアルゴリズムを紹介しました.Lassoは線形回帰と同じくらいかむしろそれ以上に使われるアルゴリズムです.慣れてくると「まずはLassoで試す」というのが当たり前になってくるぐらいです.
- 機械学習では不要な特徴量を落とすのが定石で,その方がパフォーマンスが上がることが多い
- 正則化項\(\lambda\sum_{j=1}^{n}|\theta_j|\)を損失関数に追加することにより,係数の値がペナルティの役割をして自動で特徴量の係数が0になっていく
- \(\lambda\)はLassoにおける重要なパラメータで,\(\lambda=0\)の時線形回帰となり,\(\lambda\)を大きくするとそれだけペナルティが高くなり係数を小さくし,結果多くの特徴量を落とすことになる
- Lassoを使う前には標準化をし,それぞれの特徴量のマグニチュードを等しくし,正則化による影響を揃える必要がある
- sklearn.linear.model.Lasso を使って簡単にLassoを使うことができる
次回の記事ではkNN回帰という別の回帰のアルゴリズムを紹介します.今まで紹介したアルゴリズムは線形回帰がベースになっていて,数式でモデリングできるパラメトリックな手法でした.kNN回帰は数式モデルを使わないノンパラメトリックな手法です.kNN回帰も線形回帰と双璧を成すくらい重要な回帰アルゴリズムなので是非次の記事で学習を進めて下さい!
それでは!
追記)次回の記事書きました!