データサイエンス入門の機械学習編第29回です.(講座全体の説明と目次はこちら)
追記)機械学習超入門動画講座を公開しました!動画で効率よく学習をしたい人はこちら(現在割引クーポン配布中です)
前回の記事では回帰の決定木について解説をしました.決定木は回帰だけではなく分類にも使えるアルゴリズムです.
今回の記事では分類の決定木のアルゴリズムを解説します.とは言っても,アルゴリズムの流れはほとんど同じなので,前回の記事の内容をベースに分類用に必要なところだけ付け加えて解説していきます!
また,決定木を小さくする手法であるcost complexity pruningについても解説します.よく使われるアルゴリズムなので是非この機会にものにしましょう!
目次
回帰の決定木と分類の決定木の違い
基本的なアルゴリズムの流れは回帰の決定木と同じです.最初に学習データを一つの領域とし,そこから各特徴量毎に領域を二分していき,決定木を作っていきます.
違うのは”どのように分割するのか”だけです.
回帰のケースはRSS(や他の指標)が小さくなるように領域を分割していましたが,RSSは回帰用の指標でしたよね.
分類には(当然)別の指標を使います!
また,最終的な予測値には,葉に属する学習データで最も頻度が高いクラスを使ったり,クラスの割合を確率として使うこともできます.
分類の決定木の分割時の指標

これにも色々とあるんですが,今回の記事では特に有名なジニ不純度(gini impurity)を紹介します.
ジニ不純度は,英語ではgini indexと呼ばれることも多いです.よく日本語ではジニ係数と訳されることもあるんですが,経済学で使われるジニ係数(gini coeffient)とごっちゃになってしまうので,本講座ではジニ不純度と呼んでおきます.
ジニ不純度とジニ係数は似てるんですが別物だと思ってください.これらは数学的にはかなり近い関係にあって,一部同じような形になりますが,用途が違うので用語としても区別するのがいいと思います.
ジニ不純度とは?
ジニ不純度は,クラス分けをする時に,どれだけ綺麗に分けることができるかです.
つまり,分類した時にどれだけ「不純なもの」が含まれるかってことです.

では,ジニ不純度はどのような式で表されるのか見てみましょう!ジニ不純度は以下の式で定義されます.
$$G=\sum^{K}_{k=1}p(k)(1-p(k))$$
ただし,\(K\)はクラス数,p(k)はその領域でのクラス\(k\)の割合です.
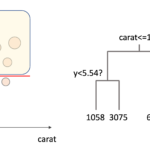
例えば以下のようにデータを分割すると(赤と青の2クラスの例)
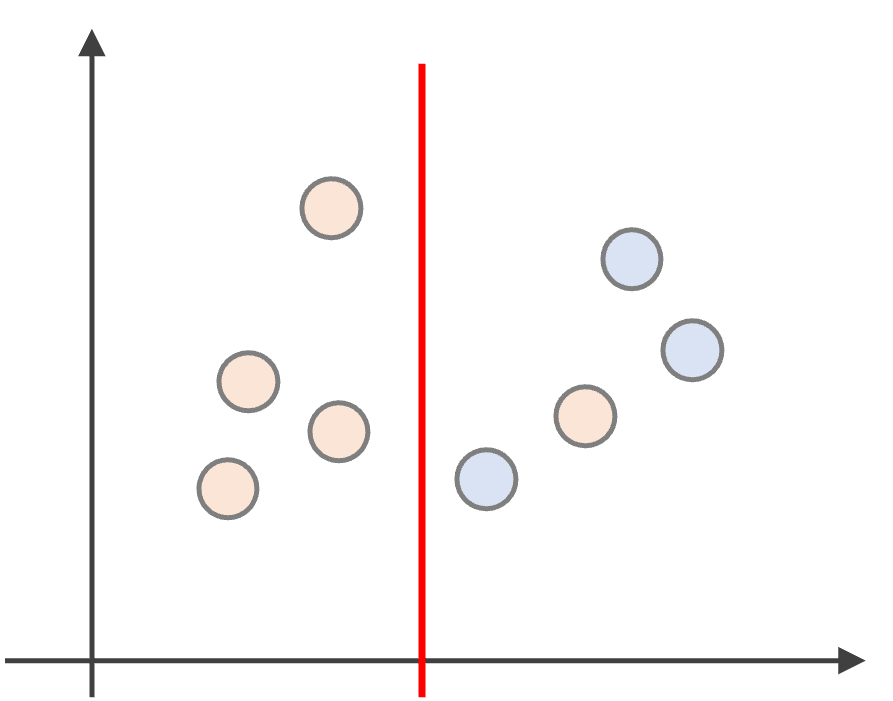
左側の領域は\(G=\frac{4}{4}(1-\frac{4}{4})+\frac{0}{4}(1-\frac{0}{4}) =0\)となり不純度0です.右側の領域は\(G=\frac{1}{4}(1-\frac{1}{4})+\frac{3}{4}(1-\frac{3}{4})=0.375\)と,少し不純度があることになります
このジニ不純度が最も低くなるように領域を2つに分けていきます.簡単ですね!
cost complexity pruningで決定木を小さくする
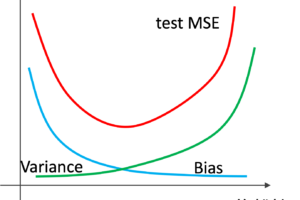
前回の記事で解説した通り,決定木のアルゴリズムを繰り返すと複雑な決定木になってしまい過学習になります.
これを避けるために,ある程度小さい木を作る必要がありますが,今回はcost complexity pruningという手法を紹介します.

これは実は名前通りの手法で,木の複雑さをペナルティのコストとしてpruning(剪定:枝を切ること)していく手法です.
式で表すとこんな感じ↓
$$R_\alpha(T)=R(T)+\alpha|T|$$
ただし\(|T|\)は決定木\(T\)の葉の数で,\(R(T)\)はその木の全ての葉での不純度の合計(回帰の場合はRSSなどの指標)です.\(\alpha\)はパラメータです.
つまり,\(R(T)\)が小さくなるように領域を二分していきますが,その木の葉の数の分だけペナルティが入る形です.これはLassoの正則化項のような役割をします.
つまり,木の葉の数が大きいと,\(R(T)\)が小さくても最終的なコスト\(R_\alpha(T)\)は大きくなってしまうため,なるべく葉の数を小さくするようにモデリングすることになります.
どの\(\alpha\)を選べばいいのかわからないので,以下のような手順で複数の\(\alpha\)を試していきます.
まず,ある枝の節点(“ノード(node)”と呼びます)に着目します.そのノード\(t\)以下の木をsubtree\(T_t\)とすると,\(T_t\)における\(R(T_t)\)は,そのノード時点での\(R(t)\)(ただしtは特定のノードを指す)よりも必ず小さくなります.
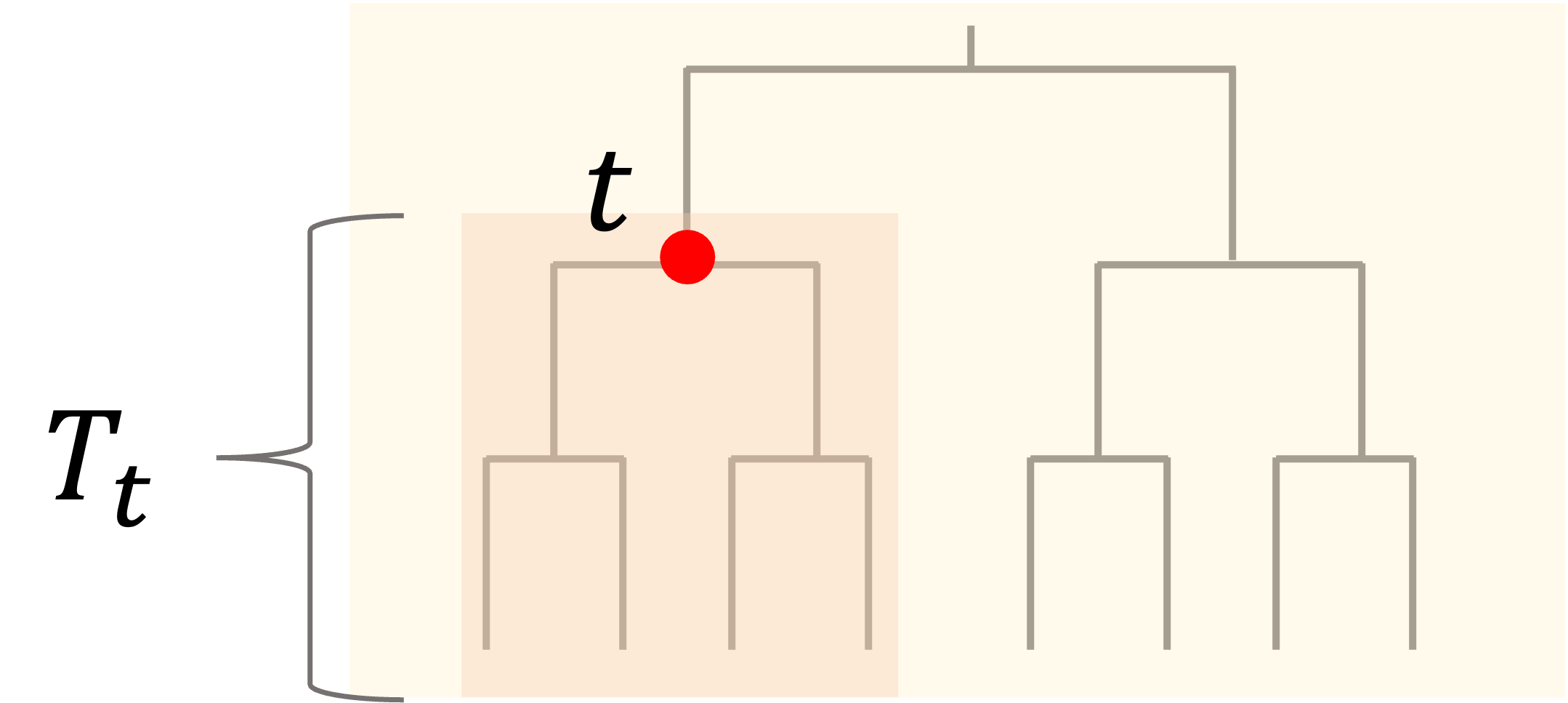
これは当然ですね.常に純度が高くなるように(回帰であればRSSが小さくなるように)分割を進めていくわけですから,どんどん\(R(T)\)は小さくなるはずです.
しかーし,\(\alpha|T|\)項がある場合そうではなくなりますよね?木の葉の数が大きくなると,それがペナルティになって,\(R(T_t)\)と\(R(t)\)が同じになる\(\alpha\)があるはずです.(この\(\alpha\)をeffective alphaと言います)
木全体のノードに対してそれぞれ\(R(T_t)\)と\(R(t)\)が同じになる\(\alpha\)を見ていき,最も小さい\(\alpha\)を持つsubtreeから剪定(pruning)していくことを考えます.
そして,最小の\(\alpha\)がある一定数に達するまでpruningをしていきます.
このやり方はscikit-learnに実装されているMinimal Cost-Complexity Pruningというやり方です.詳細は公式ドキュメントをご確認ください.

実際にscikit-learnにはこの手法が実装されているので,実際にそれを使ってどのようにpruningできるのか見てみましょう!
Pythonで決定木の分類器をpruningを使ってモデリングする
それでは,決定木の分類器バージョンをモデリングしてみましょう.
分類の決定木は, sklearn.tree.DecisionTreeClassifier クラスを使います.使い方は回帰の sklearn.tree.DecisionTreeRegressor と同じです.
前回の記事と全く同じことをしてもつまらないので,今回はpruningの処理をしてみたいと思います.
まずは前回の記事同様,データの準備をします.今回はデータサイエンスのためのPython第11回等で扱ってきたタイタニックデータセットを使います. seaborn.load_dataset を使って簡単にタイタニックデータをダウンロードすることができます.(今回はデータの詳細は割愛します.また,欠損値はシンプルに全て落とします)
|
1 2 3 4 5 6 7 8 9 10 |
import pandas as pd import seaborn as sns from sklearn.model_selection import train_test_split df = sns.load_dataset('titanic') df = df.dropna() X = df.loc[:, (df.columns!='survived') & (df.columns!='alive')] X = pd.get_dummies(X, drop_first=True) y = df['survived'] X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0) |
今回はMinimal Cost-Complexity Pruningをやってみます.
.cost_complexity_pruning_path() メソッドを使うことで,各pruning時のeffective alphaとその木の不純度を取得できます(effective alphaが上がっていくにつれて,不純度は上がっていきます.)|
1 2 3 4 5 6 |
from sklearn import tree model = tree.DecisionTreeClassifier(random_state=0) path = model.cost_complexity_pruning_path(X_train, y_train) eff_alphas, impurities = path.ccp_alphas, path.impurities print(eff_alphas) print(impurities) |
|
1 2 3 4 5 6 |
[0. 0.00656168 0.00656168 0.00699913 0.00726832 0.0077282 0.00787402 0.01049869 0.0111986 0.0118874 0.01526093 0.01880243 0.02677358 0.12717222] [0. 0.01312336 0.02624672 0.04024497 0.05478161 0.07023802 0.07811203 0.09910941 0.11030801 0.14597022 0.2375358 0.2939431 0.32071667 0.4478889 ] |
これには,モデルのインスタンス生成時に ccp_alpha 引数を指定します.
|
1 2 3 4 5 |
models = [] for eff_alpha in eff_alphas: model = tree.DecisionTreeClassifier(random_state=0, ccp_alpha=eff_alpha) model.fit(X_train, y_train) models.append(model) |
そうすると,modelsのリストに各\(\alpha\)のcost complexity pruningでのモデルが格納されるので,これらのモデルに対して精度を算出すればOKです.今回は学習データとテストデータの精度がどのように変わるのかplotしてみましょう.
|
1 2 3 4 5 6 7 8 9 10 11 |
import matplotlib.pyplot as plt train_scores = [model.score(X_train, y_train) for model in models] test_scores = [model.score(X_test, y_test) for model in models] fig, ax = plt.subplots() ax.set_xlabel("alpha") ax.set_ylabel("accuracy") ax.plot(eff_alphas, train_scores, marker="o", label="train", drawstyle="steps-post") ax.plot(eff_alphas, test_scores, marker="o", label="test", drawstyle="steps-post") ax.legend() plt.show() |
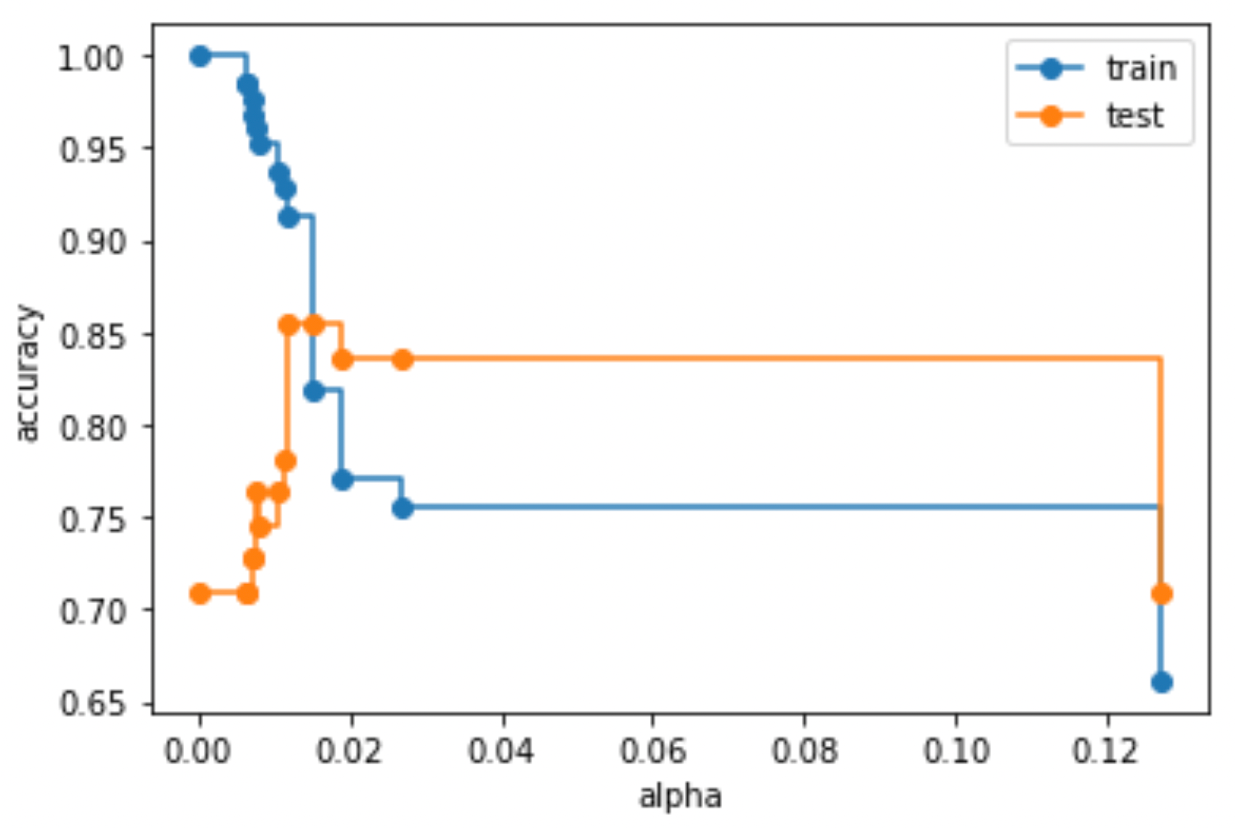
alphaが小さいうち(つまりpruningなし)は木が複雑であるが故に過学習しているのがわかると思います.
木をpruningしていくと,汎化性能が高くなっています.
実際にはk-foldCVなどで汎化性能を測るのがいいでしょう.このようにして,最適な\(\alpha\)を見つけて,cost complexity pruningで剪定した決定木を作成できます◎
興味がある人は,それぞれのモデルの可視化などをしてみてください!その辺りは前回の記事で紹介しているので今回は割愛します
まとめ
今回の記事では,分類における決定木のアルゴリズム(特にジニ不純度)と剪定アルゴリズムであるcost complexitiy pruningを紹介しました.
- 分類の決定木も回帰と同じく領域を二分して決定木を作っていく
- 分類では,ジニ不純度が小さくなるように領域を分割していく
- 複雑な決定木は過学習になるため,これを避けるために決定木をpruning(剪定)し小さくする必要がある
- cost complexity pruningは,木の大きさをペナルティ項としてコスト(不純度)に入れることで木を小さくするアルゴリズム
今回も少し長くなってしましましたが,これが決定木アルゴリズムの基礎になります.
決定木は回帰にも分類にも使える上に,非常に解釈性が高いことから色々な場面で重宝します.
もしかしたら機械学習で最も有名なアルゴリズムかもしれません(え?毎回そう言ってるって?笑)
でも間違いなく重要度高めのアルゴリズムなので,前回の記事と今回の記事で使えるようにしましょう!
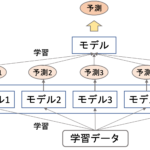
そして決定木は,複数の決定木を組み合わせることで非常に精度の高いモデルを作れることが知られています.
今多くのKaggle等のコンペの上位モデルはこのやり方を使っていると言っても過言ではありません.
次回以降はその辺りの応用的な使い方について解説をしていきます.
ここからが本講座の本番かも笑 ・・・というくらい重要な内容になってくるので,しっかり学習していいきましょう!
それでは!
追記) 次回の記事書きました!