データサイエンスのためのPython入門⑥〜はじめてのNumpy〜

こんにちは，米国データサイエンティストのかめ(@usdatascientist)です．

(「データサイエンスのためのPython講座」動画版がでました！詳細はこちら)

データサイエンスのためのPython入門も，ついに第6回まで来ました(講座の目次はこちら)．そして，ついに….

今回から本題に入れます！(長かったぜ・・・)

今回から，Pythonでデータサイエンスをするために必要なパッケージの基本的な使い方を紹介して行こうと思います.

本講座で取り扱うパッケージは以下の通りです．(予定)

NumPy
Pandas
Matplotlib
Seaborn

です．これらの紹介が終わったら，統計学と機械学習の理論をPythonを使って学習できる講座に移っていく予定．なので統計や機械学習を手を動かしてしっかり学べるようにするために，これらのパッケージの基本的な使い方をマスターする必要があるのです！

ちなみに，前回までの記事はこんな感じです↓

第一回：データサイエンスのためのPython入門①〜DockerでJupyter Labを使う〜
第二回：データサイエンスのためのPython入門②〜Jupyter Labの使い方とショートカット一覧まとめ〜
第三回：データサイエンスのためのPython入門③〜Pythonのデータタイプまとめ〜
第四回：データサイエンスのためのPython入門④〜文法まとめ1 演算子, if文, ループと内包表記〜
第五回：データサイエンスのためのPython入門⑤〜文法まとめ2 関数〜
第六回（本記事）

第六回からようやくグランドライン(本題)って感じです

なお，本講座はあくまで「Python」の入門であり「データサイエンス(統計や機械学習)の理論」を学ぶ連載ではありません．本講座でデータサイエンスに必要なPythonとそのパッケージたちを手なづけ，その後他の連載で統計や機械学習を学んでいきます．

統計とか機械学習って数学的な知識がでてくるんですけど，コードを書きながら学べた方が学習速度は速いと思います．ということで先にツールの使い方を講座にしました．

本連載はデータサイエンスを学ぶための基本的なスキルになるので絶対にマスターしましょう！

NumPyとは

なむぱい．なんだか卑猥なような美味しそうな不思議な名前ですが，科学や数学のための数値計算モジュールです．Numerical Pythonの略．

行列計算が得意で，フーリエ変換とか乱数の生成にも使えます．Pythonでデータサイエンスをするのになくてはならないモジュールです．「世界中のデータサイエンティストがPythonを使う理由はNumpyがあるから」と言っても過言ではありません．本講座で紹介するほとんどのパッケージはこのNumPyをベースに開発しているからです．

このNumPyは第一回で入れたAnacondaディストリビューションに入っています．なので，今のJupyter Labでもうすでに使えます．便利でしょAnaconda．

自分で入れる場合は $ conda install numpy や $pip install numpy で入れることができます． conda や pip はPythonのパッケージ管理ツールです．機会があればまた別途説明しますが，基本はAnacondaを使えばOKです．

importの仕方

まず，NumPyモジュールをimportする必要があります．例えば，前回の記事で関数を作った時すぐに関数名() でcallできましたよね？

それは同じページで定義していたので呼び出せたんですが，NumPyはどこか別のところに保存されているもので別途importという処理をして「NumPyを使います」宣言が必要です．その宣言によりNumPyのモジュールがメモリに乗っかり，いつでも使えるようになります．（逆にそういう仕組みにしないと全モジュールがメモリに乗って大変なことになるし，名前がかぶるとどっちを参照したらいいかわからないですから）

それではNumPyをimportします． import パッケージ名でimportできます．

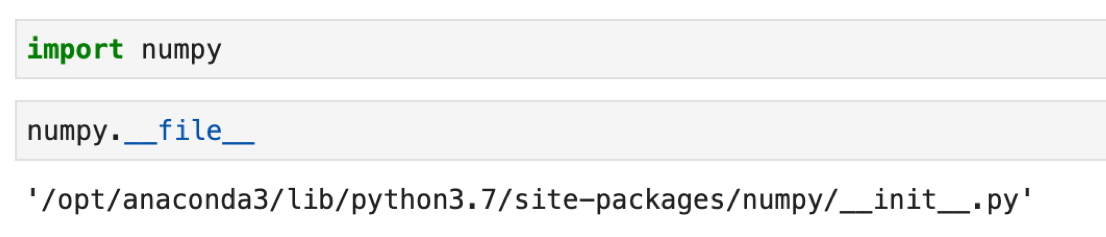
importすると numpy を使えるようになります． .__file__ で，numpyモジュールがどこにあるか確認します．

'/opt/anaconda3/lib/python3.7/site-packages/numpy/__init__.py' というところを参照しているようです． /opt/anaconda3/ は第一回で指定したAnacondaの場所です．NumPyはちゃんとAnacondaに入ってたんですね！

これでnumpyを使うようにできますが，慣習的に import numpy as np という形でimportして， numpy を np として使えるようにします．「as」というのは「〜として」と言う意味です．なので「import numpy as np」は「numpyをnpとしてimportする」と言う意味

これでnumpyではなくnpとしてnumpyモジュールにアクセスできるようになります．

行列とはなんぞ？

NumPyは行列演算が得意だと言いました．行列というのは縦と横に数字が羅列したものです．一般に，線形代数という数学の分野になります．この「線形代数」という数学の分野は，データサイエンスでは非常に重要な役割を担います．NumPyはこの「行列」の計算を簡単にしかも高速にできるのです．

今はまだ線形代数がなんなのかわからなくても，ひとまずOKです．（そのうち「データサイエンスに必要な数学入門」でもやろうかと思う

＊もしお勧めの本をお探しならこちらの記事で本を紹介しています．特にマセマの本がわかりやすくてお勧め．

データサイエンスに行列というものが必要で，「NumPyは行列演算を簡単にできる」と覚えておきましょう．

では，まず行列の説明をする前にベクトルについて解説をします．

ベクトル(Vector)

私たちが普段使っている数字は1とか1億とか，数の大きさを表しています．これをスカラーと呼びますが，ベクトルは大きさだけではなく向きの情報も持ちます．例えば速度とか力って，向きがありますよね？こういった量を表すのに，ベクトルが使われます．

もしx-y平面において向きがあるとしたら，$x$方向に3，$y$方向に2とすると「向きと大きさ」＝「ベクトル」が一意に決まります．

$$v = (3, 2)$$

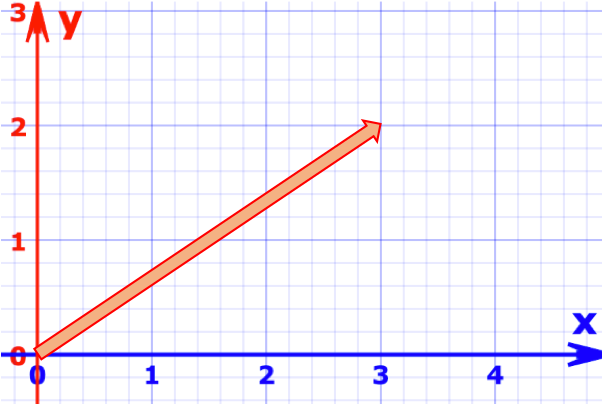
私たちの生きている現実世界は3次元なので$(3, 2, 6)$のように3次元になります．このベクトルに3というスカラーを掛けてあげると$3 \times (3, 2, 6) = (9, 6, 18)$となります．同じくベクトルの加算は$(1, 2) + (3, 4) = (4, 6)$のように，各要素単位で演算します．

ここでは数学の厳密な定義は置いておいて，「数を一列にならべたもの」がベクトルと思っていただければいいです．

行列(Matrix)

行列というのは，ベクトルを複数行もしくは列にまとめたものです．つまり，数が複数の行と複数の列に並びます．↓こんな感じ

$$M =
\begin{pmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{pmatrix}$$

データサイエンスって，とにかく沢山のデータを使うのでこういう風にデータ記述できる行列とは切っても切れないんですねぇ・・・

それではこのベクトルや行列をNumPyを使って表現してみましょう！

NumPy Arraysを使ってみる

実際にJupyterでコードを書いて実行しましょうね〜

NumPyにはNumPy Arrays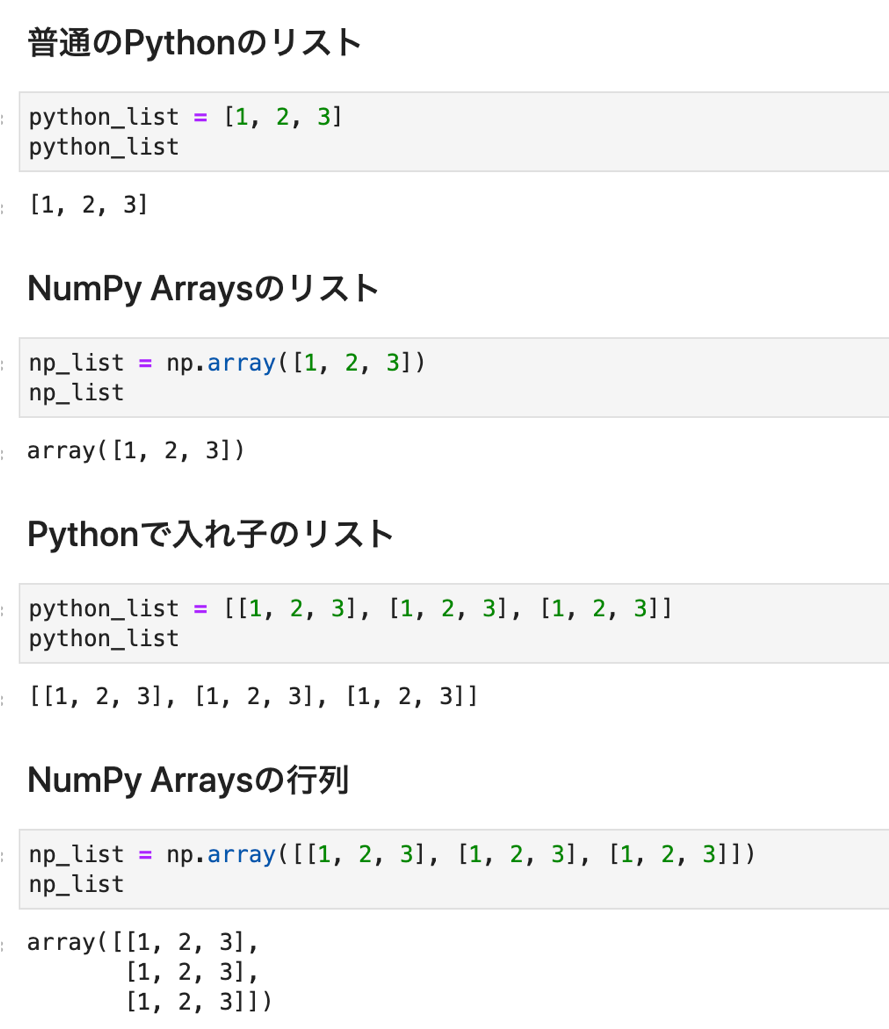というデータタイプがあり np.array() を使ってベクトルや行列を表します．

コードをサーっと眺めればなんとなくPythonのリストとの違いがわかると思います．

np.array() に [1, 2, 3] というリストを入れると[1, 2, 3]というNumPy Arrayができます．

さらに [1, 2, 3] というリストを入れ子にして [[1, 2, 3],[1, 2, 3],[1, 2, 3]] を入れると行列っぽく表示されてます．これはまさに先ほど説明した「ベクトルを複数行にまとめたもの」ですね．

これだけだと「ただ表示の仕方の問題じゃん」と思いますが，行列演算も楽にできるんです．

NumPy Arraysの演算

では以下の二つのNumPy Arraysを作って，四則演算して結果がどうなるか確認してみましょう．

array1 = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
array2 = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

1 2	array1 = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) array2 = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

結果は，要素毎でそれぞれ計算されているのがわかります．これはarrayにスカラーを四則演算しても同じです．

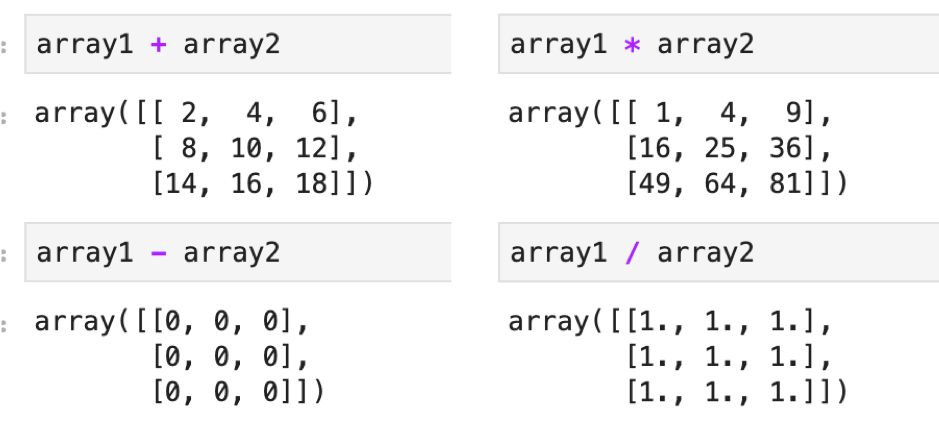
それでは試しに行列のサイズが合わない者同士で計算してみます．

array1 = np.array([1, 2, 3])
array2 = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

1 2	array1 = np.array([1, 2, 3]) array2 = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

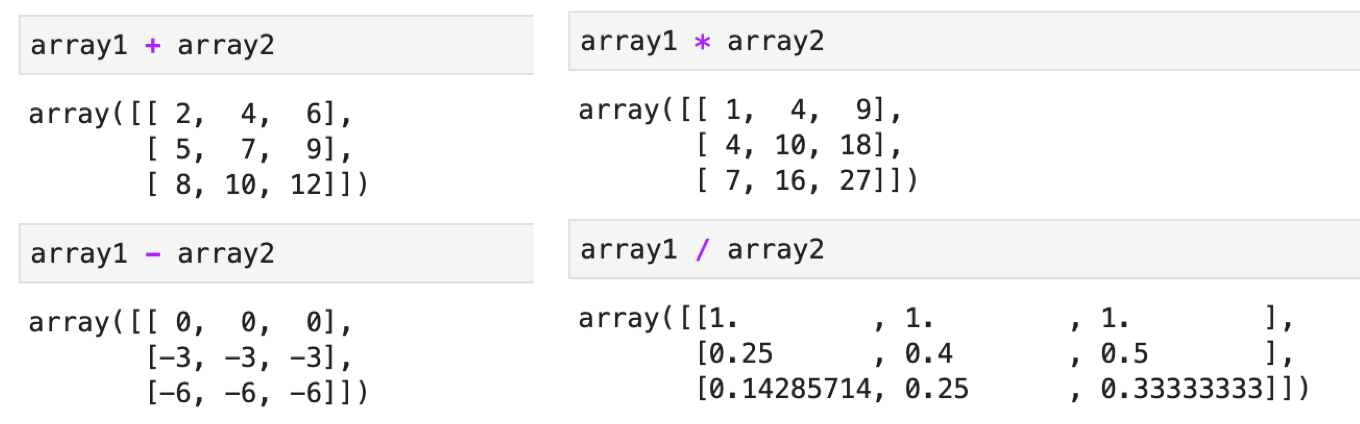
エラーにはならず，ちゃんと計算されています．計算結果をよくみると，以下の二つのarrayを計算したときと同じになってます．

array1 = np.array([[1, 2, 3], [1, 2, 3], [1, 2, 3]])
array2 = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

1 2	array1 = np.array([[1, 2, 3], [1, 2, 3], [1, 2, 3]]) array2 = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

試しに同じ計算してみてください．結果は同じです．

つまり，array1の足りない要素は[1, 2, 3]で自動的に補完されたわけです．これをBroadcastingと呼びます．このBroadcastingのおかげでNumPyは柔軟に行列計算をしてくれます．

では，要素が中途半端だったらどうなるか

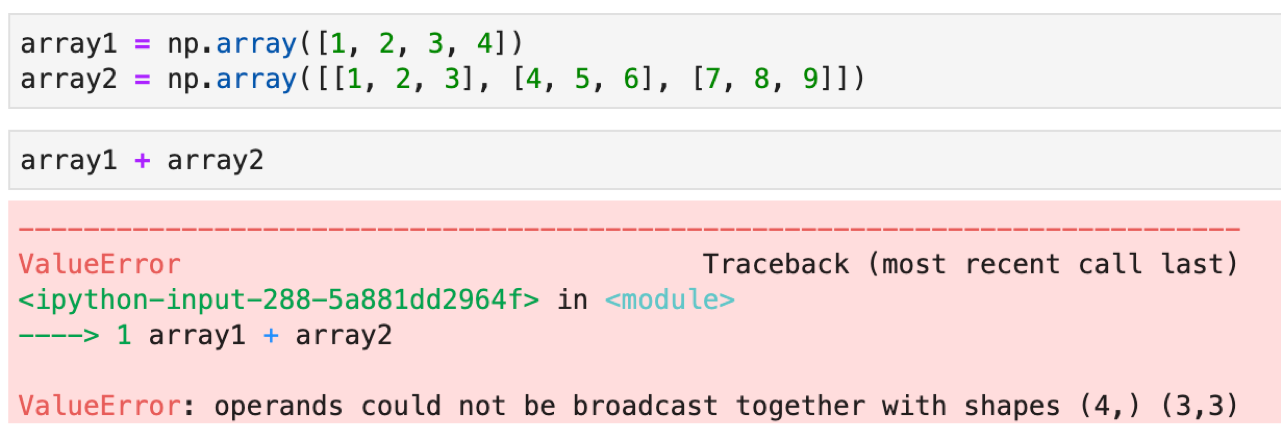
「broadcastできないよ」とエラーになりました．broadcastができる条件というのは決まってきます．

Broadcastingが可能な条件はこちらに書いてありますが，とくに覚える必要はないと思います．以下のイメージでbroadcastされるというイメージさえあれば，あとは慣れてけばOK です．ルールばかり気にしても頭に入らないので

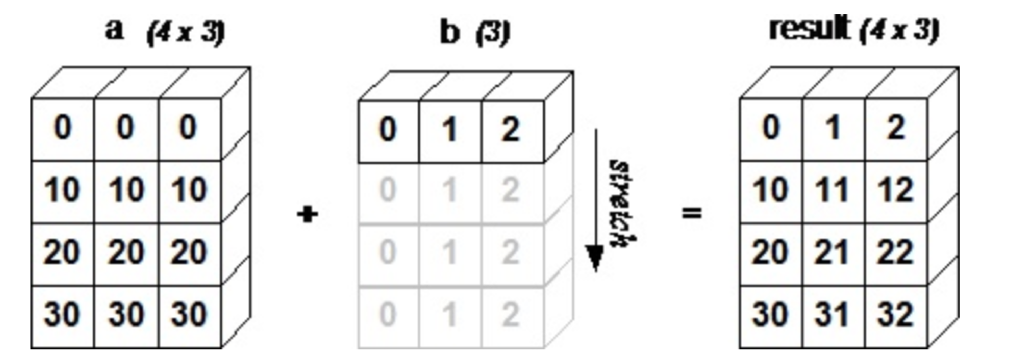
source:https://www.tutorialspoint.com/numpy/numpy_broadcasting.htm

試しにいろんなパターンで演算してみてください．なんとなくブロードキャストがどう動くかわかってくると思います．

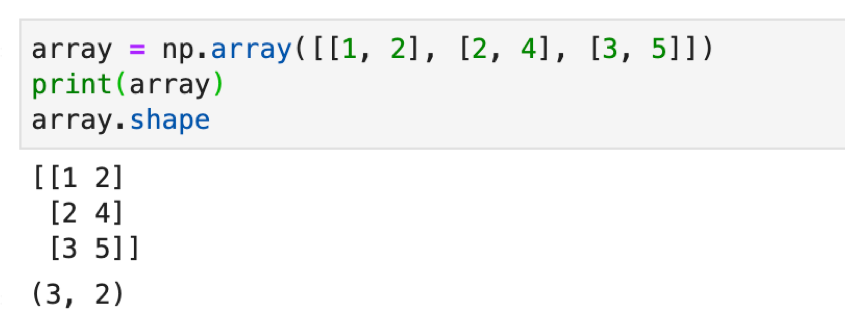
なお，NumPy Arrayの行列のサイズを確認するには .shape にアクセスします．タプルの形でサイズが返されます．(縦，横)の順です．．arrayで演算する際はよく使うので覚えておきましょう．特に画像とかを扱う時にarrayを使いますが，常にshapeがいくつなのかというのを考えながらコーディングします．