データサイエンス入門の機械学習編第22回です.(講座全体の説明と目次はこちら)
追記)機械学習超入門動画講座を公開しました!動画で効率よく学習をしたい人はこちら(現在割引クーポン配布中です)
今回の記事では超重要評価指標であるROCとAUCについて解説していきます.
間違いなく分類器で最もよく使われる評価指標です.(って,毎回言ってるだろお前って?いやいや,今回はマジですよ!!)
あまりにも有名な指標なので,「よくわからないけどなんとなく使っちゃってる」人も多いと思います.
今回の記事ではかなり丁寧にわかりやすく解説するので,しっかり学んでいきましょう!!
目次
ROCカーブとは
ROCは,Receiver Operating Characteristicの略です.はい,覚えなくて結構です.(略を知ってる人ほとんどいないと思うw)
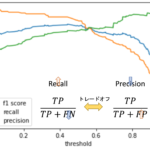
これは前回の記事のPrecisionとRecallのトレードオフの解説で,閾値を変えて行った時のPrecisionとRecallのカーブがありましたよね?
それと同じように描いたSensitivity(Recall)と1-SpecificityのカーブがROCです.
RecallとSensitivityは同じ意味なんですが,Specificityの対比でよく使われるのはSensitivityの方なので,ROCの解説では”Sensitivity”を使って解説していきます.また,SensitivityはTrue Positive Rate, 1-SpecificityはFalse Positive Rateともいいます.こちらもROCの文脈ではよく使われるので覚えておきましょう.

第20回で解説したSensitivityとSpecificityをもう一度みてみましょう
$$Sensitivity(Recall)=\frac{TP}{TP+FN}$$
$$Specificity=\frac{TN}{TN+FP}$$
Sensitivityは,陽性のデータに対してどれだけ正しく陽性と分類できたかの指標であり
Specificityは,陰性のデータに対してどれだけ正しく陰性と分類できたかの指標でした.(つまりSensitivityの陰性版ですね)

1-Specificityは,以下の式からわかるように,陰性のデータに対してどれだけ陽性と”間違えたか”です.
$$1-Specificity=1-\frac{TN}{TN+FP}=\frac{TN+FP}{TN+FP}-\frac{TN}{TN+FP}=\frac{FP}{TN+FP}$$
そのため,SensitivityがTrue Positive Rate(TPR)と呼ばれるのに対し,1-SpecificityはFalse Positive Rate(FPR)と呼ばれるのもわかると思います.(←呼び名が多すぎて辛い人は忘れてください!)
このSensitivityとSpecificityにはトレードオフの関係があります.つまり,閾値を変動させて片方を高くするともう片方が低くなります.閾値を徐々に変えていった時にSensitivityと1-Specificityがどのように推移していくかを表したグラフがROCです.
PythonでROCを描画する
それでは実際に前回の記事で作ったHeart disease datasetのロジスティック回帰の結果を使ってROCを描画してみたいと思います.
実際の業務でもROCを描画することは本当によくあります.分類器を作ったらほぼ必ず描画すると言ってもいいくらい一般的に使われる図なので,是非自分で書けるようにしておきましょう!
データの準備と前処理は前回の記事を参考にしてください.今回は前処理後のコードから書いていきます(全部書いていたらまた記事が長文になってしまうので・・・!!)
前回の記事の前処理が終わると,dfは以下のようになっています.
|
1 |
df.head() |

前回の記事同様,学習データとテストデータに分割し,ロジスティック回帰でモデルを学習させます.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
from sklearn.linear_model import LogisticRegression from sklearn.model_selection import train_test_split # 学習データとテストデータ作成 X = df.loc[:, df.columns!='target'] y = df['target'] X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0) # モデル構築 model = LogisticRegression(solver='liblinear') model.fit(X_train, y_train) # 予測(確率) y_pred_proba = model.predict_proba(X_test) |
ここまでは前回の記事と同じです.やはりscikit-learnにはROCカーブを簡単に描画できる関数が用意されています.
sklearn.metrics.roc_curve を使います.これは前回の記事で紹介した sklearn.metrics.precision_recall_curve と同じように使うことができ,第一引数に y_true , 第二引数に特定のラベルについての確率のリストである y_score を指定します.戻り値は fpr , tpr , thresholds の3つのリストで,それぞれの名前の通り,False Positive Rate (1-Specificity),True Positive Rate (Sensitivity),閾値が返ってきます.この辺りも sklearn.metrics.precision_recall_curve と同じ感じですね!
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
import matplotlib.pyplot as plt from sklearn.metrics import roc_curve %matplotlib inline # 陽性の確率だけが必要なので[:, 1]をして陰性の確率を落とす pos_prob = model.predict_proba(X_test)[:, 1] fpr, tpr, thresholds = roc_curve(y_test, pos_prob) # 描画 plt.plot(fpr,tpr) plt.xlabel('1-specificity (FPR)') plt.ylabel('sensitivity (TPR)') plt.title('ROC Curve') plt.show() |
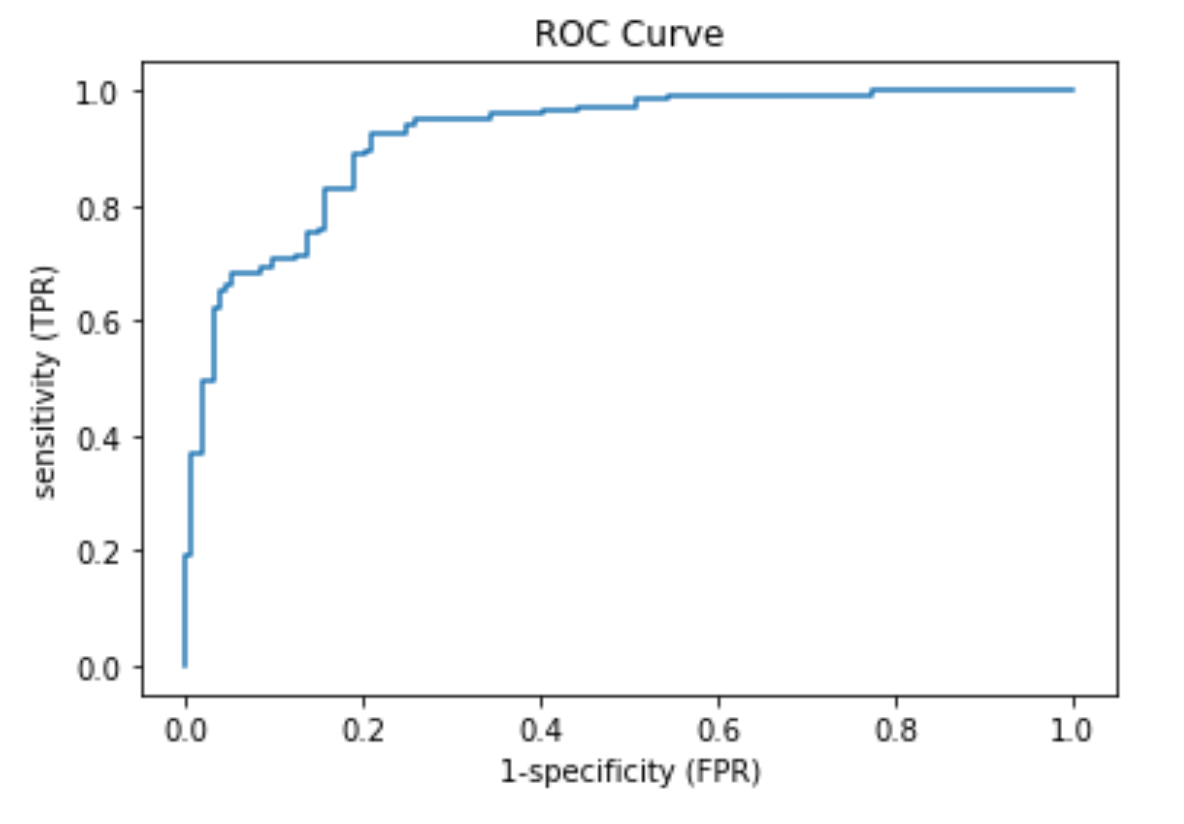
はい,これがROCカーブです!!
横軸に1-Specificity(False Positive Rate)を,縦軸にSensitivity(True Positive Rate)をとり,閾値を変えていったときのそれぞれの値の推移をplotしています.
閾値が1だと,全てのデータをNegative(陰性)に分類するので,\(Sensitivity=\frac{TP}{TP+FN}\)は0になり,\(Specificity=\frac{TN}{TN+FP}\)は1になります.この閾値を下げていくと徐々にSensitivityは上がっていきSpecificityは下がっていきます.(ROCでは横軸には1-Specifitiyをとっていることに注意しましょう)
閾値が0になると,全てのデータをPositive(陽性)と分類し,Sensitivityが1になり,TNが0になるためSpecificityは0になります.
このように,SensitivityとSpecificityの間にもトレードオフがあることがわかると思います.
AUCはROCカーブが作る面積

ROCカーブが作る面積が大きいと精度が高いモデルとなります.そしてこの面積をAUC(Area Under the Curve)といいます.”ROCに対しての”と特筆する場合は,AUROCと言ったりしますが,単にAUCというと普通はROCの面積を指します.
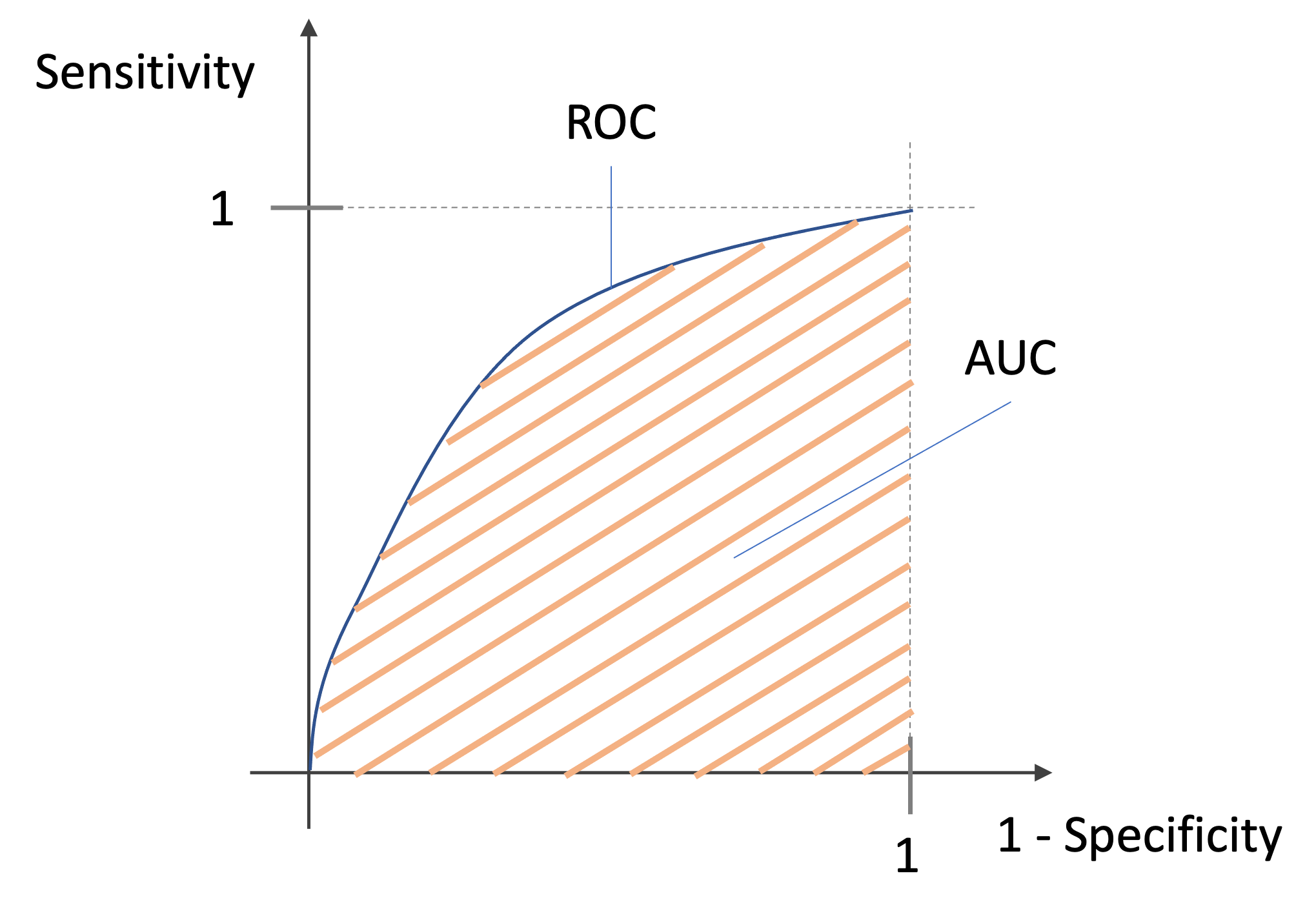

ROCには,以下の特徴があります.
- 当てずっぽうに予測する完全ランダムなモデルのROCは対角線になる
- 全てのデータに正しく予測できる完璧なモデル(確率も完全に100%と0%のみで正しく言い当てれるモデル)のROCは正方形の形になる
つまり以下の図のように,ROCが描く線の下の面積が小さくなれば精度は低く,大きければ精度が高いモデルになるのです.(興味がある人はさきのコードを参考にランダムな値と完璧な値でROCを書いてみてください.)
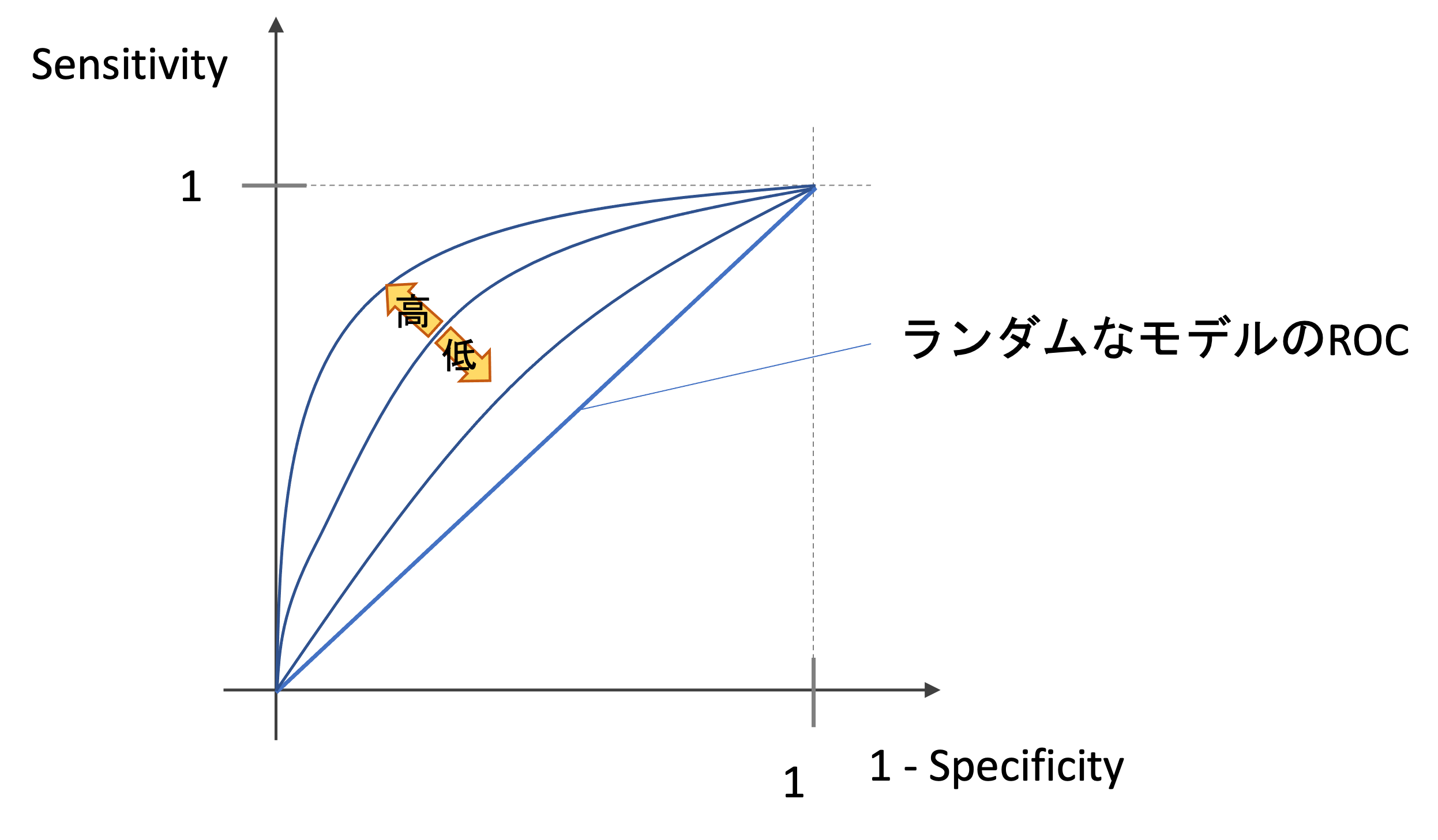
つまり,AUCがとりうる値は0〜1ですが,ランダムなモデルのAUCが0.5であることを考えると,普通は0.5~1に収まると考えていいでしょう.
感覚ですが,AUCが0.8以上あると精度が高いという印象があります.が,これは当然データやタスクの種類によるので一概には言えません.
PythonでAUCを計算する
当然scikit-learnにはAUCを簡単に計算してくれる関数 sklearn.metrics.auc が用意されています.
第一引数にx軸の値のリスト x を,第二引数にy軸の値のリスト y を入れます.つまり,先ほどの roc_curve() の戻り値である fpr と tpr を入れてあげればOKです.
|
1 2 |
from sklearn.metrics import auc auc(fpr, tpr) |
|
1 |
0.9196762141967622 |
今回のROCは0.92ということで,結構高いですね.(一般的には)精度がいいモデルだと言えるでしょう.(もちろん,どれくらいの精度を求めるかはアプリケーションによりますが…)
まとめ
今回は分類器を評価する上で非常に重要な精度指標であるROCとAUCについて解説しました.
- ROCは,横軸に1-Specificity (False Positive Rate),縦軸にSensitivity (True Positive Rate)をとり,閾値を変えていった時にそれらの指標がどう推移するかを表したグラフ
- SpecificityとSensitivityはトレードオフの関係にあり,ROCはそれを表している
- ROCが描くカーブの下の面積が高い方が精度がいい.この面積のことをAUCと呼ぶ
- AUCは最高1で,ランダムに分類するモデルの場合0.5となる
ROCを使って閾値を決定することもできます.アプリケーションによってSensitivityとSpecificityがどれくらい必要なのかがわかれば,ROCから閾値を決めることができるでしょう.SpecificityではなくPrecisionを見たいのであれば,前回の記事のPreicisionとSensitivity(Recall)のカーブを見ればOKです.
このようにその分類器を使うアプリケーションやユースケースによって,最適な評価指標を選ぶことが重要です!
次回の記事では多クラス分類におけるROCとAUCの計算の仕方を解説します.実際の業務で多クラス分類を扱うことは多いので,是非このまま学習を進めていきましょう!
それでは!
追記) 次回の記事書きました