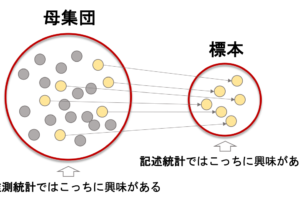
前回の記事からデータサイエンス入門講座の機械学習編の記事を書いています.(講座全体の説明と目次はこちら)
今回の記事と次回の記事で,学習データを使って線形回帰のアルゴリズムをどのように学習させていくのか解説していきます.
機械学習の肝となるアルゴリズムの部分ですので,かなーり噛み砕いて丁寧に解説するのでついてきてください!
目次
損失関数とは
機械学習で予測モデルを構築する際には,損失関数(loss function)と呼ばれる関数によって計算された値を最小にするように学習を進めていきます.

大丈夫,そんなに難しく考える必要はなくて,実は当たり前のことを言っているだけなのです.
線形回帰の例を見てみましょう.
線形回帰のアルゴリズムでは,最小二乗法により\(f(X)=\theta_0+\theta_1X_1+\theta_2X_2+\cdots+\theta_nX_n\)のパラメータである\(\theta_0, \theta_1, \cdots, \theta_n\)を求めて最適な線形の式を計算するんでした.
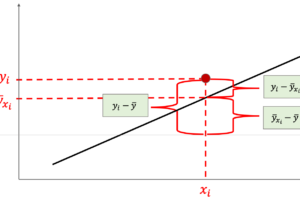
最小二乗法は,残差の二乗和を最小にするアルゴリズムです.言い換えると,「残差の二乗和を”損失”(loss)と考えて,その損失を最小にする」アルゴリズムと言えます.(前回の例でいうと以下なイメージ)

当然損失を0にすることはできませんが(厳密にいうと非線形のモデルを使えばできます.が,学習データに対して損失が0になるというのはそれはそれで問題ありなのです.これについてはまた今後の記事で書いていきます),ここでは一旦,損失を最小にしていくことを目指します.(実際には学習データの損失ではなくテスト用のデータの損失をみることになりますが,これについてはまた別記事で解説します)
残差の二乗和は以下の式で表されるんでした.(わかりやすくするために,前回の例と同じ特徴量一つのみのケースで書いてます)
$$\sum^{m}_{i=1}{e_i^2}=\sum^{m}_{i=1}{\left\{y_i-(\theta_0+\theta_1x_i)\right\}^2}$$
この式の変数を\(\theta_0\)と\(\theta_1\)と考えると,上の式は\(\theta_0\)と\(\theta_1\)の関数であると言えます.
このような「予測値と正解値のズレを計算する関数」のことを損失関数や目的関数といい,よく英語ではcost functionやloss function, objective functionと呼ばれています.
機械学習の文脈ではよく損失関数(loss function)やコスト関数(cost function)と呼びますが,もう少し広い分野の統計学や最適化の文脈では,最適化する目的の関数ということで目的関数(objective function)と呼ぶことが多いです.本講座では特に気にせず損失関数と呼んでおきます
線形回帰では,上記の残差の二乗和を損失関数として使ってもいいんですが,計算を楽にするために残差の二乗の平均を使うことが多いです.これをMSE(mean squared error)と呼ぶので覚えておきましょう.学習データにどれくらい回帰がfitしているかの指標として最も使われる指標です.
$$MSE=\frac{1}{m}\sum^{m}_{i=1}(y_i-\hat{f}(x_i))^2$$
MSEは線形回帰に限らず「残差の二乗の平均」と定義されるので,\(\hat{f}(x_i)\)の形を使いました.(\(\hat{f}(x_i)\)については前回の記事を参考にしてください).特徴量が一つの線形回帰であれば,\(\hat{f}(x_i)=\theta_0+\theta_1x_i\)に置き換えて
$$MSE=\frac{1}{m}\sum^{m}_{i=1}(y_i-(\theta_0+\theta_1x_i))^2$$
とすればOKです.また,このMSEの式は先ほども述べたように\(\theta_0\)と\(\theta_1\)を変数とした関数ですね.これを\(L(\theta_0, \theta_1)\)としておきます.
損失関数の可視化

色々やり方があるのですが,ここでは最も一般的なやり方を紹介します!
が,まずは
$$L(\theta_0, \theta_1)=\frac{1}{m}\sum^{m}_{i=1}(y_i-(\theta_0+\theta_1x_i))^2$$
という関数がどのようなグラフになるのかみてみましょう! パラメータが\(\theta_0, \theta_1\)の二つなので,3次元の図になりますね.(例えば\(f(x)=ax+b\)という関数であれば,変数は\(x\)のみなので横軸に\(x\),縦軸に\(f(x)\)をとった2次元の図になります.もう一つパラメータが増えたら次元が増え3次元になりますよね
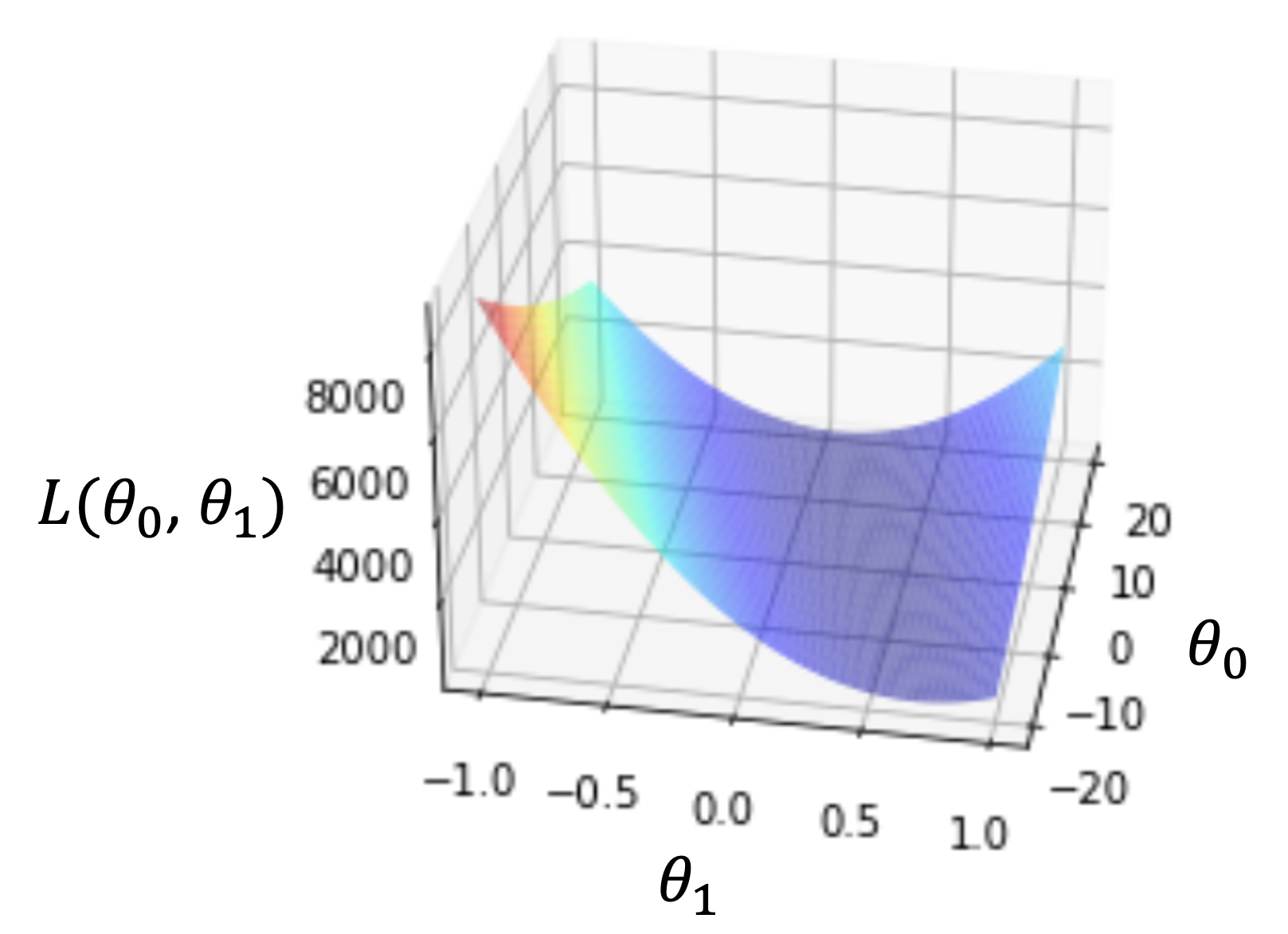
上図は実際に\(\theta_0\)を-20〜20,\(\theta_1\)を-1〜1のときの\(L(\theta_0, \theta_1)\)を計算してplotした行った時の図です.
3次元の図ではわかりにくいので,等高線図を使ってみましょう.同じ線上では値が同じになるように線を引いていきます.(標高がわかるような図ですね)
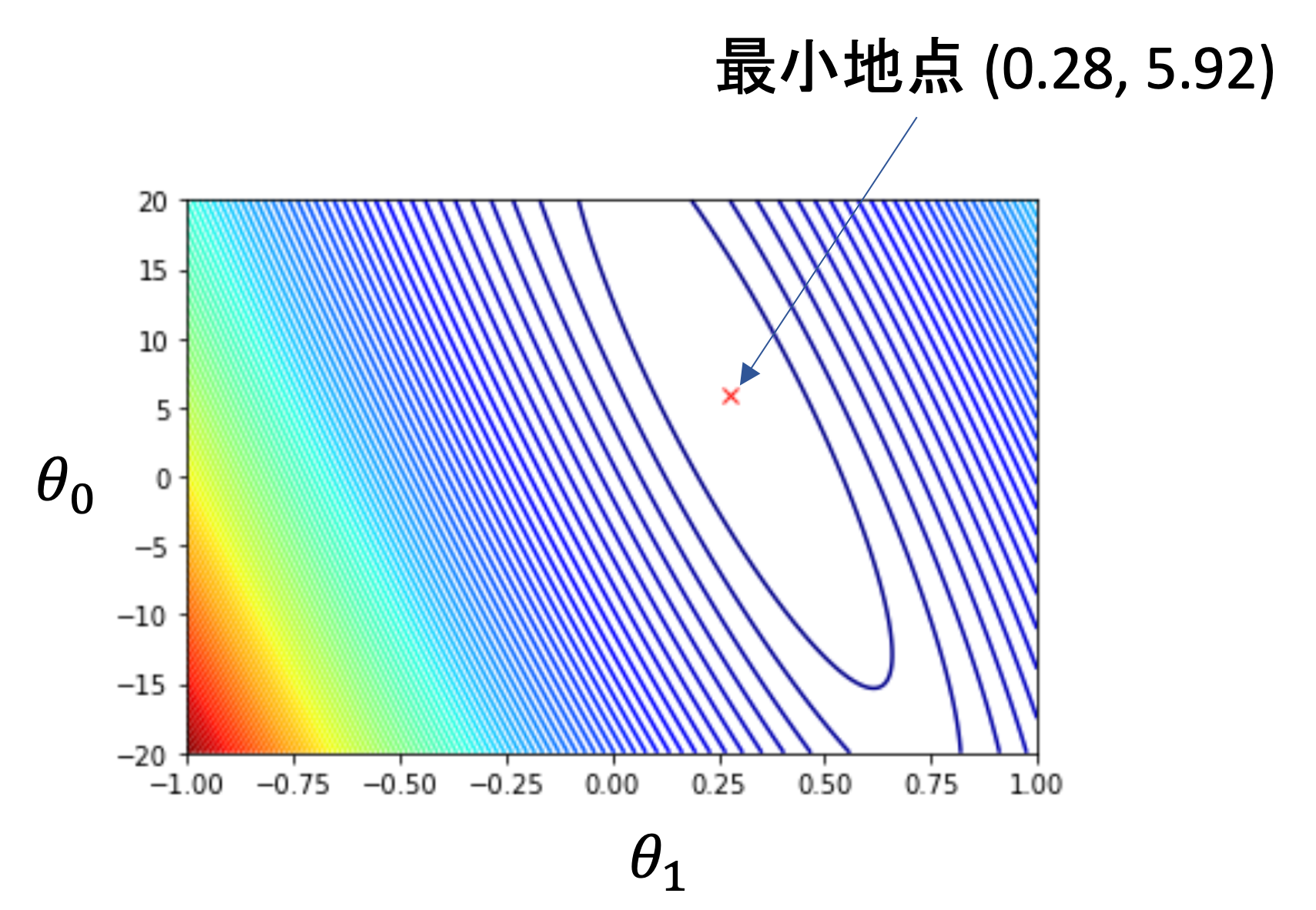
3次元の図にて坂が急なところは線同士が近く,緩やかなところでは線同士が離れていきます.最も\(L(\theta_0, \theta_1)\)が小さくなる点は\(\theta_0=5.92, \theta_1=0.28\)です. この最小になる点こそが,求めるべき\(\theta_0\)と\(\theta_1\)なのですが,これは本来わかりません.
最急降下法で最適解を見つける

これは通常,簡単に求めることができません.今後の記事でやりますが,線形回帰の場合は一発で出す方法があります.が,一般的な機械学習の文脈ではこれを一発で計算して求めることはできません.ではどうするのか?
「簡単に求めることができない」というのは,数式を変形したりして解くことができないことを意味します.このようなことを「解析的に解けない」問題と言います.
そこで登場するのが最急降下法(gradient descent)というアルゴリズムです.これは最適化問題の勾配法と呼ばれるアルゴリズムの一つなんですが,最急降下法というのは,ある点から最も傾きがある方向に少しだけ動かして,またその点から最も傾きがある方向に少し動かして,,,というのを反復していき,最終的に解となる最小地点を見つけるやり方です.
以下のような図をイメージするとわかりやすいと思います!
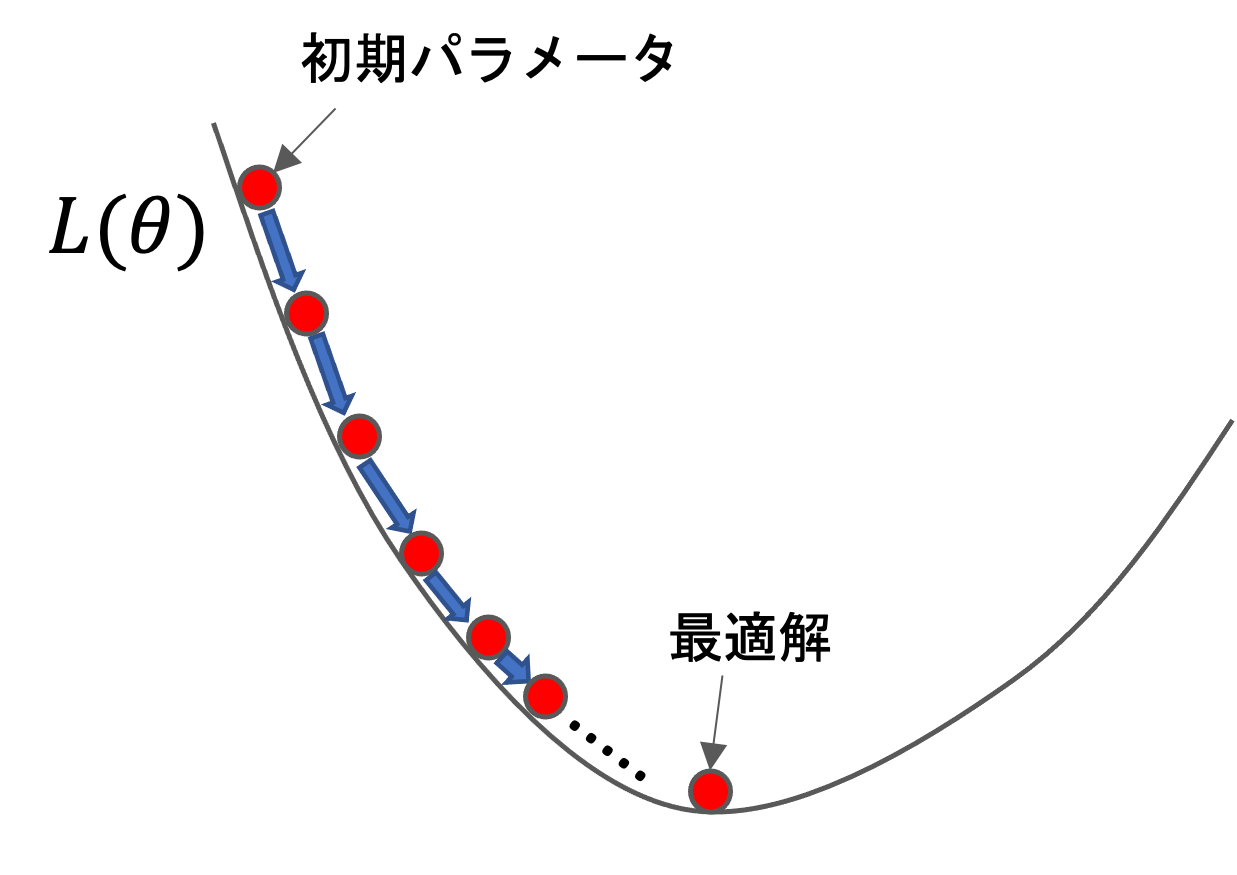
こんなような\(L(\theta)\)のグラフがあったら,初期パラメータを任意の点(通常はランダム)に置いてそこから徐々に最も急な方向に少し動かして,またそれを繰り返し,徐々に最適解にたどり着く感じです.

そして機械学習ではこのように,パラメータを徐々に最適解に近づけていくことを「学習する」と言います.(最急降下法以外にもパラメータの最適解を求める手法はありますし,解析的に解けるアルゴリズムもありますが,そのような場合でも一概に「学習する」と言います)
次回の記事では実際にこの最急降下法を数式化して,具体的にどういう計算をしていくのかを紹介していきます!
追記)機械学習超入門動画講座では実際にコードを書いて最急降下法を実装し,上記のような3Dの図を描画するところもやります.実際に手を動かしてスクラッチで実装することでより理解が深まるので,是非受講ください!(↓の記事に割引クーポンあります.是非お使いください!)
まとめ
今回は,損失関数と最急降下法の導入部分について触れました!
これらは機械学習の肝となる部分なので,是非今回の記事と次回の記事でしっかり学習しましょう.
- 損失は損失関数により計算することができる
- 損失が最小になるようなパラメータを見つける
- 通常解析的に解を求めることができないので,最適化問題を解く
- 最も勾配が急になっている方向にパラメータを徐々に移動させて最適解を求める方法を最急降下法と呼ぶ
次回の記事では最急降下法についてもう少し詳しく解説していきます!超重要な部分です
それでは!
追記)次回の記事書きました!