超わかりやすい！不偏分散がn-1で割る理由！不偏性とは【統計学入門⑦】

こんにちは，米国データサイエンティストのかめ(@usdatascientist)です．

（追記）全16時間の統計学動画講座を公開しました！☆4.8の超高評価をいただいている講座です．こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください．

前回の記事で，不偏分散というのは母集団の分散の推定量だという話をし，標本分散$s^2$は母集団分散$\sigma^2$に比べ小さく評価されがちだという話をしました．

今回の記事では，不偏分散の“不偏”とは一体どういう意味なのか，なぜnではなくn-1で割るのか，これらについて説明していきたいと思います．

統計学を学び始めた全員が疑問に思う箇所でありかつ，ちゃんと理解するのが難しい箇所でもあります．

結論からいうと，

不偏分散は，母集団分散の不偏推定量なので”不偏”という文字がついている
ある推定量が“平均的に”母集団のパラメータと一致する場合，この推定量は不偏であるといい，そのような推定量を不偏推定量と呼ぶ
n-2もn-3でもなくn-1で割る理由なんて別に知らなくていい．が，一応証明する

こんな感じです．

もう何言ってるのかわからないのでこのブログ閉じてNetflix観て寝ます！

大丈夫，全部わかりやすく解説するから！！統計学の基本的な考え方がたくさん詰まってるので，頑張ってついてきてください！

また，今回の記事では第一回で紹介した推測統計の範囲に少し踏み入れていきます．

不偏性とは

前回の記事で，母集団の分散と標本の分散を計算してこう思った人もいるでしょう．

「標本の分散が母集団の分散より小さくなるので，標本分散より小さい不偏分散を推定量として使うことはわかったけど，それでもそれが別に母集団の分散と一致するわけではないし，抽出した標本によってその値はまちまちだから，何をもって”推定量”と言っているのだろう」

そうですよね，ここでは簡単な例として母集団の平均$\mu$を推定することを考えてみましょう．母集団の平均$\mu$を推定するのに標本の平均$\bar{x}$を使えるという話は前回の記事でしましたね．

では，以下のコードをみてみましょう．前回のコードから少し変えて，母集団からランダムに5つの値を抽出し，平均を計算します．

import numpy as np
population = np.array([1, 5, 10, 11, 14, 15, 15, 16, 18, 18, 19, 20, 25, 30])
# ランダムに値を抽出
samples = np.random.choice(population, size=5)
print('population mean is {}'.format(np.mean(population)))
print('sample mean is {}'.format(np.mean(samples)))
print('samples: {}'.format(samples))

import numpy as np

population = np.array([1, 5, 10, 11, 14, 15, 15, 16, 18, 18, 19, 20, 25, 30])

# ランダムに値を抽出

samples = np.random.choice(population, size=5)

print('population mean is {}'.format(np.mean(population)))

print('sample mean is {}'.format(np.mean(samples)))

print('samples: {}'.format(samples))

何度か実行してみてください．どうでしょう？標本の平均が母集団の平均とぴったり一致するわけではないですよね？抽出された値によって平均も変わるのでそれは当然のことです．

これを例えば1万回繰り返したら，1万個の標本平均を計算することができます．その平均をとったらどうなりますか？(ややこしいですが，つまり，標本平均$\bar{x}$の平均です．)

やってみましょう．

import numpy as np
population = np.array([1, 5, 10, 11, 14, 15, 15, 16, 18, 18, 19, 20, 25, 30])
# ランダムに値を抽出
print('population mean is {}'.format(np.mean(population)))
# 標本平均をこのリストに入れていく
sample_mean_list = []
count = 10000
# for文で回すことで何度も標本抽出をする
for i in range(count):
    #標本抽出
    samples = np.random.choice(population, size=5)
    #標本平均をリストに格納する
    sample_mean_list.append(np.mean(samples))
print('sample_mean_list mean is {}'.format(np.mean(sample_mean_list)))

import numpy as np

population = np.array([1, 5, 10, 11, 14, 15, 15, 16, 18, 18, 19, 20, 25, 30])

# ランダムに値を抽出

print('population mean is {}'.format(np.mean(population)))

# 標本平均をこのリストに入れていく

sample_mean_list = []

count = 10000

# for文で回すことで何度も標本抽出をする

for i in range(count):

#標本抽出

samples = np.random.choice(population, size=5)

#標本平均をリストに格納する

sample_mean_list.append(np.mean(samples))

print('sample_mean_list mean is {}'.format(np.mean(sample_mean_list)))

ちょっと長いですが，やってることは難しくないです．この辺りのコードが難しく感じるようであれば，是非先にPython講座をやっておきましょう！文法はわかるけど自分で書いたりすることができない！っていう人は，是非コミュニティDataScienceHubのCoding Challengeにチャレンジしてください．毎週コーディングの課題+コーディングレビューもしてるので効率よく上達することができます．コードを書きながら統計学を学んだ方が，実践的かつ体験できるので，本などで数式を眺めるよりよっぽど効率がいいです．

結果は例えばこんな感じです．

population mean is 15.5
sample_mean_list mean is 15.5386

1 2	population mean is 15.5 sample_mean_list mean is 15.5386

1万回母集団から標本を抽出して計算した1万個の標本平均の平均は，母集団の平均にかなり近くなりますよね？これをさらに10万, 100万と増やしていけばもっと近くなります．(上のコードで count 変数を変えてみましょう)

このように，標本平均は母集団の平均から大きかったり小さかったりまちまちなんですが，それを無限回繰り返した無限個の標本平均$\bar{x}$の“平均”は母集団の平均$\mu$に限りなく近くなります．

このように，ある推定量が”平均的に”母集団のパラメータと一致する場合，この推定量は不偏(unbiased)であるといい，そのような推定量を不偏推定量(unbiased estimator)と呼びます．これが不偏性というやつです．平均的に一致するので”偏り”が無い(“不“)推定量なわけです．

つまり，標本平均$\bar{x}$は母集団平均$\mu$の不偏推定量です．

不偏性や不偏推定量は，重要な単語なのでちゃんと使えるようにしましょう！

じゃぁ分散はどうなのよ？

無限個の標本分散$s^2$の平均は，母集団の分散$\sigma^2$とは一致しません．それは前回の記事を読んでいればわかりますよね？

無限個の標本の不偏分散の平均こそが，母集団の分散$\sigma^2$と一致するのです．なので，n-1で割った分散を“不偏”分散というのですね．

先ほどのコードを修正して，試しに分散と不偏分散を1万回計算してその平均を母集団の分散と比べてみてください．前回の記事と前々回の記事を読んでいれば簡単に書けると思います．

期待値という考え方

なぜn-1で割るのかの説明をする前に，期待値について簡単に解説しておきます．

「期待値」

日常生活でも使ったことありますよね？1000円の宝くじを買ってる人に対して「でもそれ，期待値は400円くらいでしょ？」とか「今年の新人の期待値はマジで高い」とかとか．

一個目の例と二個目の例では意味合いが違いますが，まぁどちらも「何かに対して期待する値」ですよね？1個目の例は確率的に期待する値で，２個目の例ではただたんに物事に対する期待の度合いです．

ここで説明するのは１個目の例です．では，「1000円の宝くじの期待値が400円」というのは，どういうことでしょうか？

それは，宝くじを買えば”平均的に”400円が返ってくるということですよね？(もちろん，宝くじでは一部の人だけが大金を得ることができますが，それを購入者全員で”平均”したら400円になるということです．)

つまり，理論的な平均値ということですね．単に平均と言ってもいいですが，確率の概念がある場合は，その平均値のことを期待値(expected value)ということが多いです．(まぁこれもあまり気にする必要はないかもしれませんが)

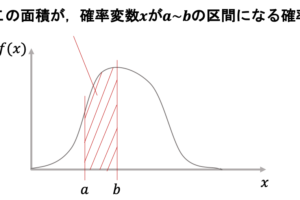
ここで，ある確率的に変動する値（これを確率変数と呼びます．例えば宝くじの賞金や，サイコロをふった時の目の値など）を$x$とすると，期待値は以下のように表します．

$$E(x)$$

なにも難しいことはないですね，例えばサイコロの目を$x$とすると期待値$E(x)$は

$$E(x)=\frac{1+2+3+4+5+6}{6}=3.5$$

ということになります．簡単ですね．

ここで，今まで求めてきた標本の平均や標本の分散なんかも，確率的に変動する確率変数なので，以下のように表せることができます．(標本平均も標本分散もランダムに抽出した値から計算するので，当然確率的に変動するものですよね？詳しくは第18回にて解説してます！)

つまり，標本平均$\bar{x}$の期待値$E(\bar{x})$は母集団平均$\mu$と一致するということです．(標本平均は母集団平均の不偏推定量なので)

$$E(\bar{x})=\mu$$

これは，以下のように考えれば簡単に証明することができます．

\begin{eqnarray}
E(\bar{x})&=&E[\frac{1}{n}(x_1+x_2+\cdots+x_n)]\\
&=&\frac{1}{n}E[(x_1+x_2+\cdots+x_n)])\\
&=&\frac{1}{n}(E(x_1)+E(x_2)+\cdots+E(x_n))\\
&=&\frac{1}{n}n\mu=\mu
\end{eqnarray}

同じ母集団からランダムに取ってきた値$x$の期待値$E(x)$は当然$\mu$ですよね？なので$E(x_1)$も$E(x_2)$も全て$\mu$になります．

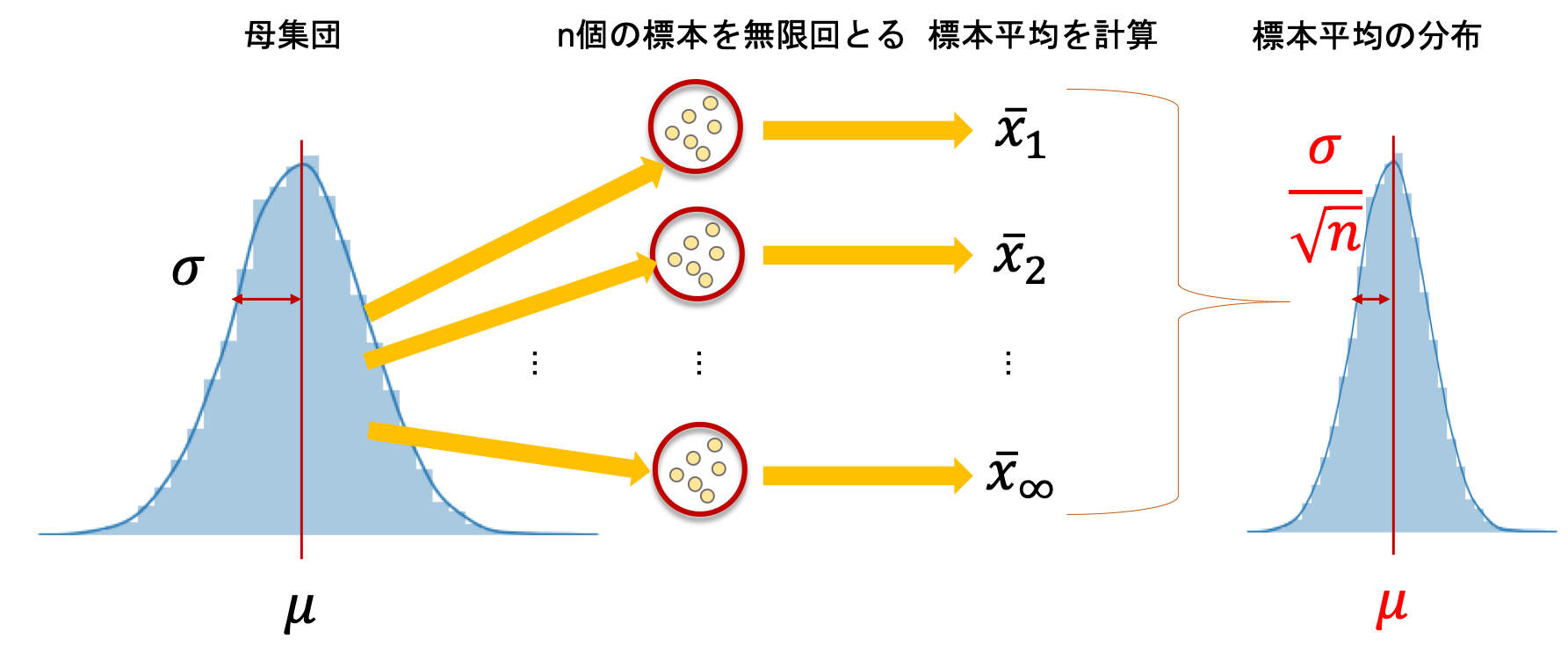
また，標本平均$\bar{x}$の分散の期待値$E[\frac{1}{n}\sum{(\bar{x}-\mu)^2}]$は$\frac{\sigma^2}{n}$になることが知られています．(これ，あとで使います．)

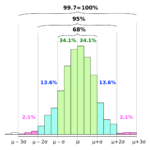
これも非常に重要なので覚えておきましょう！(証明は飛ばしますが，これもイメージが大事です．n=1のとき，一個しか標本を取らなかったら取ってきた値自体が標本平均になるので，その分散は母集団分散$\sigma^2$と一致しますね．逆にnが非常に大きいと，毎回の標本平均は母集団平均$\mu$に近くなるので分散は小さくなるのがわかると思います！)

図で言うとこんな感じですね！(分散ではなく標準偏差を記述しています．)

さて，ここまできたら，標本分散の式でnで割るところをn-1で割ると，その期待値がちょうど母集団の分散$\sigma^2$と一致することを証明することができます．

不偏分散がn-1で割る理由

先に言っておくと，この証明は別に重要ではないです．知らなくてもOK．

普通に業務でデータサイエンスをやる分にはこの証明ができる必要なんて全くありません．

なので，興味無い人は「まとめ」に飛んで，次の記事に進みましょう．

さて，母集団の分散$\sigma^2$というのは，標本内で，母集団の平均$\mu$からの偏差の平方和の平均の期待値であると言えます．(無限回標本を取ってきて，$\mu$からの偏差の平方和を無限回計算した平均ですよね，，うーん，ややこしい！笑)

つまり

$$\sigma^2=E[\frac{1}{n}\sum{(x_i-\mu)^2}]$$

です．ここで，右辺を標本平均$\bar{x}$を使ってうまく書き換えます．

ここまではOKでしょうか？あと少しです！標本分散の期待値$E[\frac{1}{n}\sum{(x_i-\bar{x})^2}]$を左辺に移項すると，
\begin{eqnarray}
E[\frac{1}{n}\sum{(x_i-\bar{x})^2}]&=&\frac{\sigma^2}{n}-\sigma^2\\
&=&\frac{n-1}{n}\sigma^2\\
\end{eqnarray}

となることがわかると思います．この最後の式はなにを言っているのか．

これは，標本の分散$\frac{1}{n}\sum{(x_i-\bar{x})^2}$の期待値(つまり，標本を無限回抽出して無限個計算した標本分散の平均値)は，母集団の分散$\sigma^2$よりも$\frac{n-1}{n}$だけ小さく計算されるということです．

これは言い換えれば，標本分散$\frac{1}{n}\sum{(x_i-\bar{x})^2}$に$\frac{n}{n-1}$を掛けたら期待値は母集団の分散$\sigma^2$と一致するということですね！

これで，不偏分散がn-1で割っている理由が分かったと思います．

この証明自体は別に難しくないので，興味ある人は是非数式を追っていただきたいのですが，まぁこの証明ができなくてもデータサイエンティストとして生きていけるので，そんな重要ではないです．