(追記)全16時間の統計学動画講座を公開しました!☆4.8の超高評価をいただいている講座です.こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください.
Pythonで学ぶデータサイエンス入門:統計編第14回です.
前回の記事で回帰分析について解説しました.
最小2乗法によって回帰直線の式\(y=a+bx\)を求めることができるという説明をしましたが,
- 実際に\(a\)と\(b\)はどういう値になるのか.
- Pythonで実際に回帰直線の式を求めるにはどうしたらいいのか
今回の記事ではこのあたりを解説していこうと思います.
理論的にも非常に重要ですし,実際にPythonで回帰直線を求めることは結構あると思います!
数式についてはイメージできるよう図を使ってわかりやすく伝えますので,是非ついてきてください.(イメージできることがとにかく重要です.)
目次
回帰直線y=a+bxの式を求める
前回の記事で最小2乗法により以下の式を最小にする\(a\)と\(b\)を求めていきます.数式による導出は重要ではないので,今回はその結果と,その結果が意味することをイメージできるようにしましょう.(導出よりもイメージできることの方が重要です)
$$\sum^{n}_{i=1}{\left\{y_i-(a+bx_i)\right\}^2}$$
この式には\(a\)と\(b\)の2つの変数があります.「最小にする」ということは微分して0になる\(a\)と\(b\)を求めればいいわけですが,このように変数が複数ある場合は,\(a\)と\(b\)でそれぞれ偏微分して0になる式を作り,その二つの式の連立方程式を解けばOKです.(興味がある人はやってみてください.)
え?なにを言ってるかわからない?わからなくてよろしい!とにかく,最小2乗法によって回帰直線の式\(y=a+bx\)を求めると,以下のようになります.
$$a=\bar{y}-b\bar{x}$$
$$b=r\frac{s_y}{s_x}$$
です.(ただし,\(r\)は\(x\)と\(y\)の相関係数,\(\bar{y}\)と\(\bar{x}\)はそれぞれ\(y\)と\(x\)の平均)
いきなり結果だけ「どん!」って出されてもしっくりこないですよね?大丈夫です.今から超わかりやすくこの二つの式が意味することとそのイメージを解説します.数式よりも,これが何を意味するのかのイメージを持つことの方がよっぽど重要です.
まず一つ目の\(a=\bar{y}-b\bar{x}\)ですが,これは\(\bar{y}=a+b\bar{x}\)と変形できることからイメージしやすいと思います.これは,回帰直線が\(x\)と\(y\)の平均である\((\bar{x}, \bar{y})\)を通るということです.
どういうことかというと,(前回までの記事で使っていた height と weight の例でいきましょう.身長から体重を予測することを考えるので,x軸は身長(height), y軸は体重(weight)です)
|
1 2 3 4 5 6 7 8 9 10 |
import numpy as np import matplotlib.pyplot as plt import seaborn as sns %matplotlib inline weight = np.array([42, 46, 53, 56, 58, 61, 62, 63, 65, 67, 73]) height = np.array([138, 150, 152, 163, 164, 167, 165, 182, 180, 180, 183]) plt.scatter(height, weight) plt.xlabel('height') plt.ylabel('weight') |
(この辺りのコードがあやしい人は,本ブログのデータサイエンスのためのPython講座を先に読むことをお勧めします.コードを書きながら実際のデータをいじることが統計学を学ぶ上で必須です.まじでそれ以外無いと思うくらい・・.)

実行すると,こんな散布図になると思います.
ここに「身長から体重を予測する」線を引きたいわけですよね?そしたら,当然データの真ん中あたりの点を通るように引くと思います.この”真ん中”のイメージがまさに点(\(\bar{x}, \bar{y})\)なんですね.
|
1 2 3 4 |
plt.scatter(height, weight) plt.plot(np.mean(height), np.mean(weight), 'ro') plt.xlabel('height') plt.ylabel('weight') |

つまり,回帰直線は(\(\bar{x}, \bar{y})\)を通る傾き\(b=r\frac{s_y}{s_x}\)の直線ということですね.
では次に直線の傾き\(b=r\frac{s_y}{s_x}\)をみていきましょう.これは傾きなので,(簡単にいうと)y軸方向の増加分\(\div\)x軸方向の増加分 ですよね?
|
1 2 3 4 |
sns.regplot(height, weight) plt.plot(np.mean(height), np.mean(weight), 'ro') plt.xlabel('height') plt.ylabel('weight') |
(前回紹介した sns.regplot() を使って回帰直線を描画しています.)
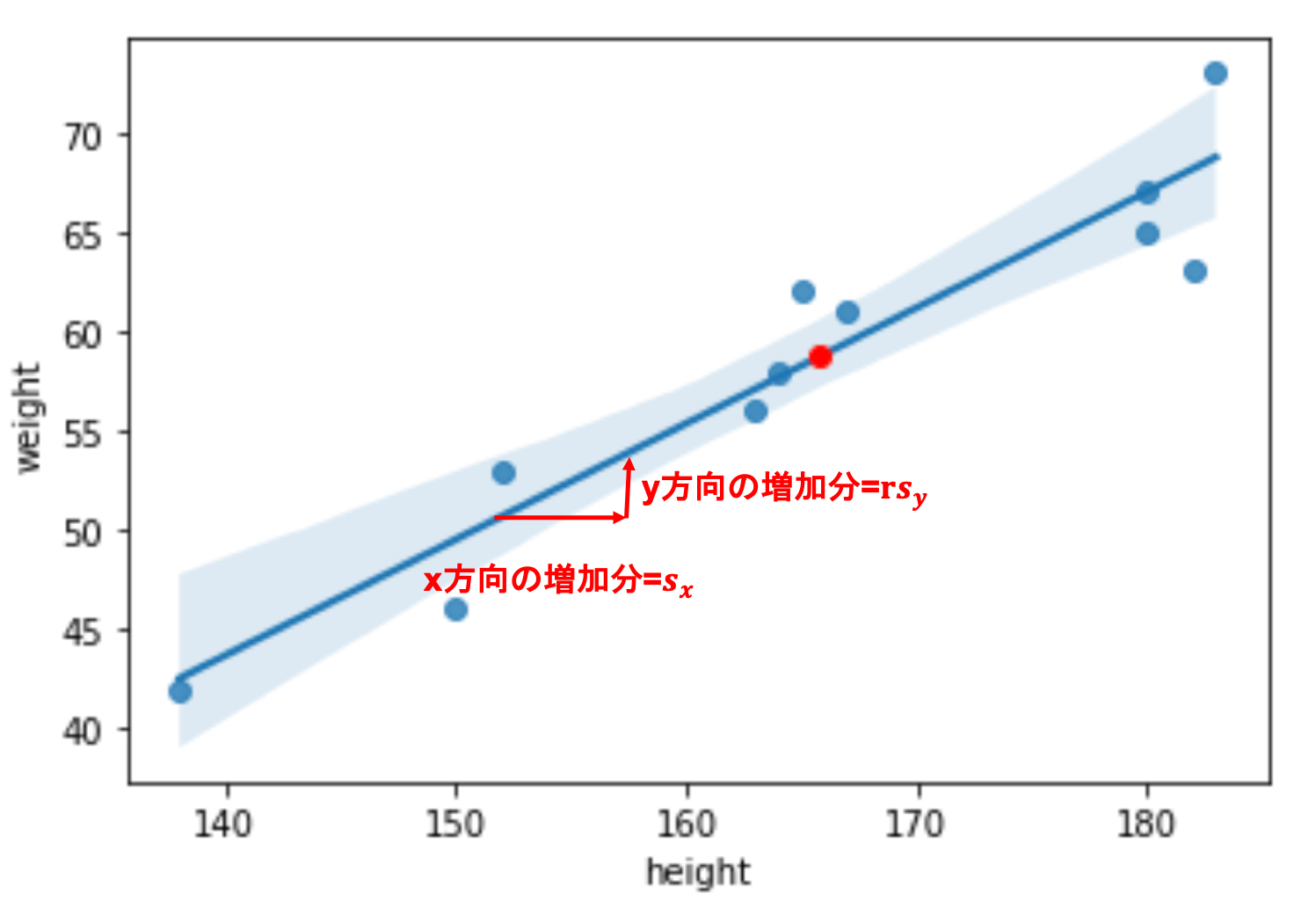
(図の赤い矢印は必ずしも正しいサイズではなくイメージですが)\(b=r\frac{s_y}{s_x}\)が意味していることは,x軸方向に\(s_x\)増加すると,y方向に\(rs_y\)増加するような直線であるということです.
これは以下のようにイメージするとわかりやすいです.
変数が3つ(\(s_x, s_y, r\))もあるので,まずは\(r\)が1と仮定して,\(s_x\)と\(s_y\)について見てみましょう.
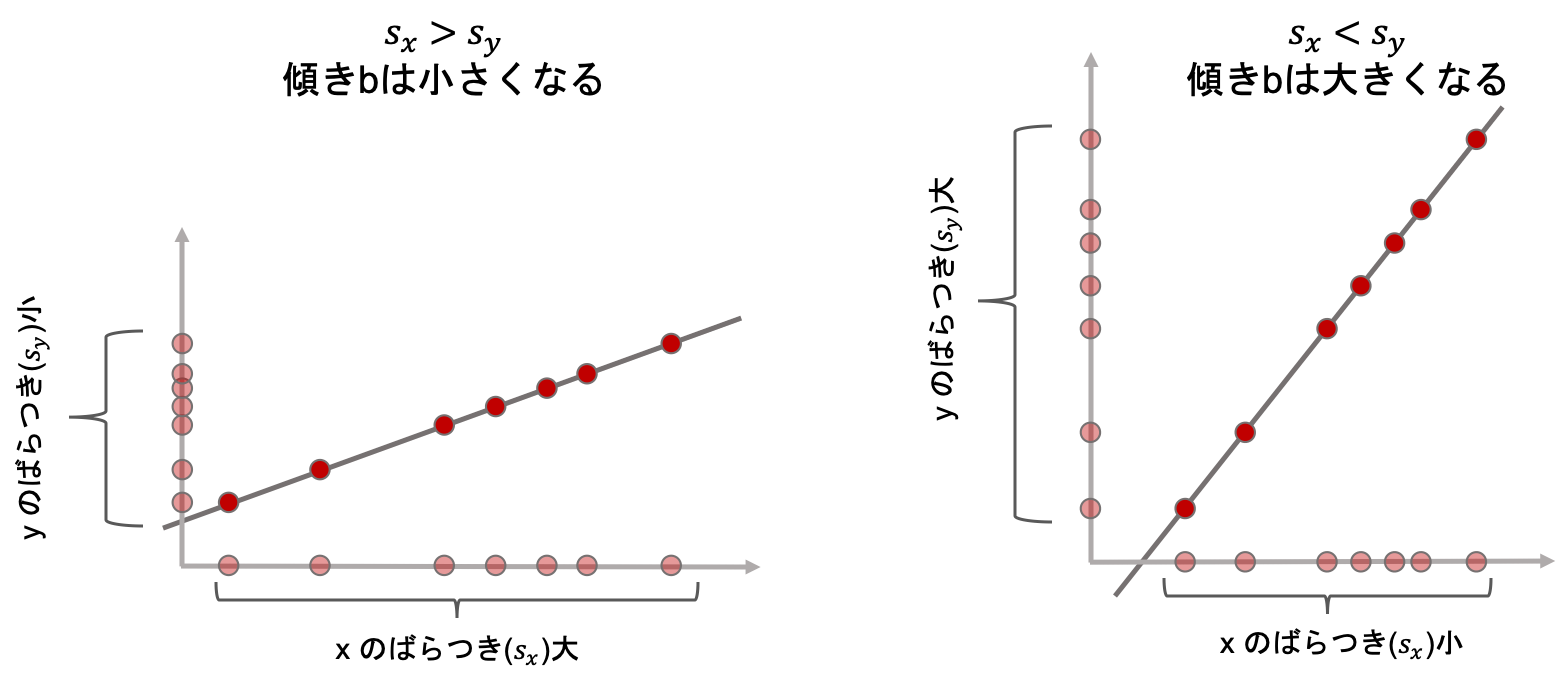
左の図と右の図を見比べてみてください.
相関係数が1の場合,xとyのばらつきの比(\(\frac{s_y}{s_x}\))に応じて傾きbの大きさが変化するのがわかると思います.(\(s_y\)が0だったら,点はx軸方向にのみ並ぶので,傾きは0になるのがわかると思います.)
どうやら傾きは確かにxとyのばらつきの比(\(\frac{s_y}{s_x}\))に比例しそうです.
次に相関係数\(r\)についてみていきましょう!
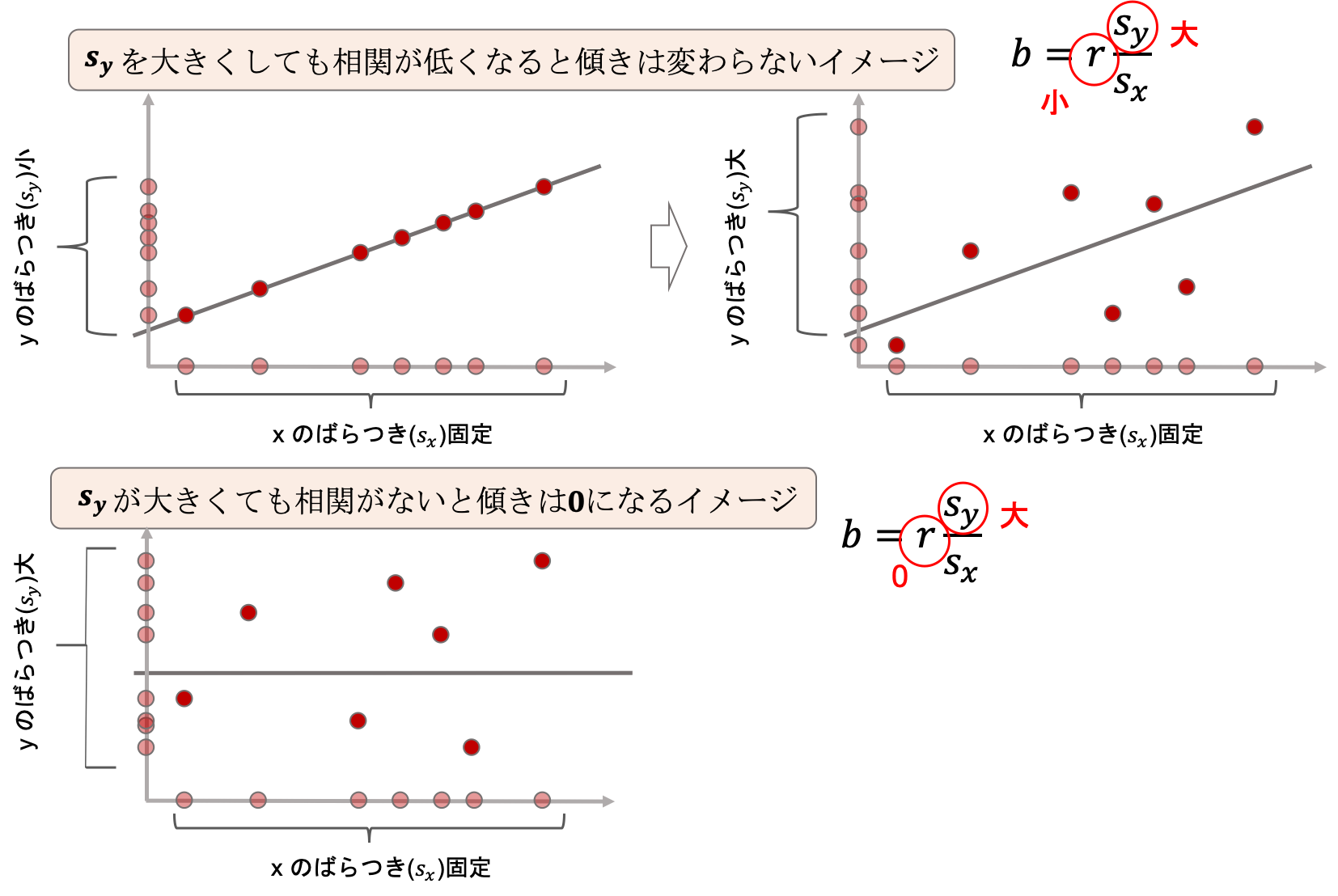
まず上の左右の図を見比べてください.xのばらつきを固定したまま,左ではyのばらつきが小さく相関係数が1, 右ではyのばらつきが大きく相関係数が<1です.
\(s_y\)が大きくなったからといって,傾きが大きくなるかといったらそういうわけでもないのはイメージできると思います.相関が低いと傾きも小さくなります.\(s_y\)と相関係数\(r\)が相殺して,傾きが変わらないイメージを持つといいと思います.
どんなに\(s_y\)が大きかろうが相関が無いのであれば,回帰直線の傾きは限りなく0に近づいていきます.(上述の下図参照)
なんとなくイメージ出来ましたか?これが回帰直線が相関係数と密接な関係にある理由です.(なお,上の図はあくまでイメージです.点と直線は適当に書きました.)
とにかく重要なのは,回帰直線は\((\bar{x}, \bar{y})\)を通る傾きが\(r\frac{s_y}{s_x}\)の直線ということです.イメージと一緒に覚えておきましょう!
また,この傾き\(b=r\frac{s_y}{s_x}\)のことを回帰係数(regression coefficient)と呼ぶのでこれも覚えておきましょう!
Pythonで回帰直線を求めてみる
それでは,実際にPythonでheightからweightを予測する回帰直線を求めてみましょう!
Pythonで回帰直線を求めるにはscikit-learnライブラリのlinear_modelモジュールにあるLinearRegressionというクラスを使います.
回帰は機械学習のアルゴリズムの一つとして使われるので,scikit-learnを使うんですね.(例えば身長から体重を予測する回帰直線を引けたら,そのデータにない新たな身長のデータに対してもその回帰直線を使えますよね?つまり,この回帰直線はすでにあるデータで学習済みのもの(モデル)だと捉えることができます.詳しくは機械学習の講座で話したいと思います.)
回帰直線,つまり線形回帰(linear regression)は線形の機械学習のモデルなのでlinear_modelモジュールの中に入っています.
別に覚える必要は無いです.ググればすぐにでてきます.
さて,LinearRegressionはsklearnにあるモデルなんですが,sklearnのモデルの使い方があるのでそれに沿ってコーディングしていきます.
そんなに難しくないんですが,まだ機械学習の話をしていないので100%理解する事は難しいと思うのと,今回はあくまでも統計学の講座なので「こういうものなんだ」くらいに思っていただければOKです.詳しくはまた機械学習編で扱うこととします.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
from sklearn.linear_model import LinearRegression #① 説明変数は,shapeが(サンプル数,特徴量数)のndarrayにします.特徴量数は,今回は身長だけなので1ですね. X = np.expand_dims(height, axis=-1) #② 目的変数のshapeは(サンプル数)でOKなのでこのまま使います. y = weight #③ インスタンスを作ります. reg = LinearRegression() #④ .fit()関数で,そのモデルのアルゴリズムを与えられたデータで"学習"することができます. reg.fit(X, y) #すると'reg'が学習済みのモデルになります. #回帰係数(b)と切片(a)はそれぞれ以下のようにしてアクセスすることができます. # .coef_はndarrayで返ってきます.shapeはX.shape次第です. print("b={}".format(reg.coef_)) print("a={}".format(reg.intercept_)) |
sklearnのモデルは, X と y を引数にして .fit() 関数を実行することで学習することができます.
回帰直線も一種の機械学習のアルゴリズムであり,”学習”することで予測することができる”予測モデル”です.通常, X は行列(shape=(サンプル数, 特徴量数))なので大文字, y は目的変数の羅列なのでベクトルの扱いということで小文字で変数を作ります.
今回のように,説明変数として使用する変数のことを機械学習の文脈では特徴量(feature)と呼びます.特徴量についてはまた機械学習編で詳しく解説します.
今回はheightという変数(特徴量)だけなので, np.expand_dims() を使ってrankを2にしました.この辺りはこちらの記事で解説しています.また,この辺りのNumPyの次元が難しい!という人はこちらの動画講座で,CTデータを使ってビジュアル的にかなりわかりやすく説明しています.
さて,基本的な LinearRegression() クラス(に限らずsklearnのモデル全般)の使い方は,
1.インスタンス(今回は reg )を作成し,
2. .fit() 関数をコールします.するとそのインスタンスが学習済みのモデルとなります.
学習ができたら, .coef_ と .intercept_ でそれぞれ回帰係数\(b\)と切片\(a\)にアクセスすることができます.
回帰係数はndarrayで返されます.この辺りは機械学習編で詳しく解説します.今回はそういうものだと思っていただいてOKです.
さて,結果をみると
|
1 2 |
b=[0.58302859] a=-37.94946808510638 |
このようになっていると思います.きちんと
$$a=\bar{y}-b\bar{x}$$
$$b=r\frac{s_y}{s_x}$$
になっているのか確かめてみましょう!
|
1 2 3 4 5 6 7 8 9 10 11 12 |
#標準偏差 s_x = np.std(height) s_y = np.std(weight) #平均 mean_x = np.mean(height) mean_y = np.mean(weight) #相関係数 r = np.corrcoef(weight, height)[0][1] b = r * s_y/s_x a = mean_y - b*mean_x print("b={}".format(b)) print("a={}".format(a)) |
|
1 2 |
b=0.5830285904255318 a=-37.94946808510635 |
きちんとsklearnの結果と一致しているのがわかると思います!
( np.corrcoef() については第11回, np.mean()や np.std() についてはこちらの記事をご確認ください.)
さて,それでは求めた式\(y=a+bx\)をplotしてみましょう!このような数式をplotするやり方はこちらの記事でも解説してます.
|
1 2 3 4 5 6 7 |
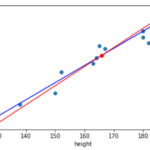
#x軸の値作成 x = np.arange(130, 190, 1) plt.plot(x, b*x+a, ) # seaborn のregplotも合わせて描画する. sns.regplot(height, weight) plt.xlabel('height') plt.ylabel('weight') |
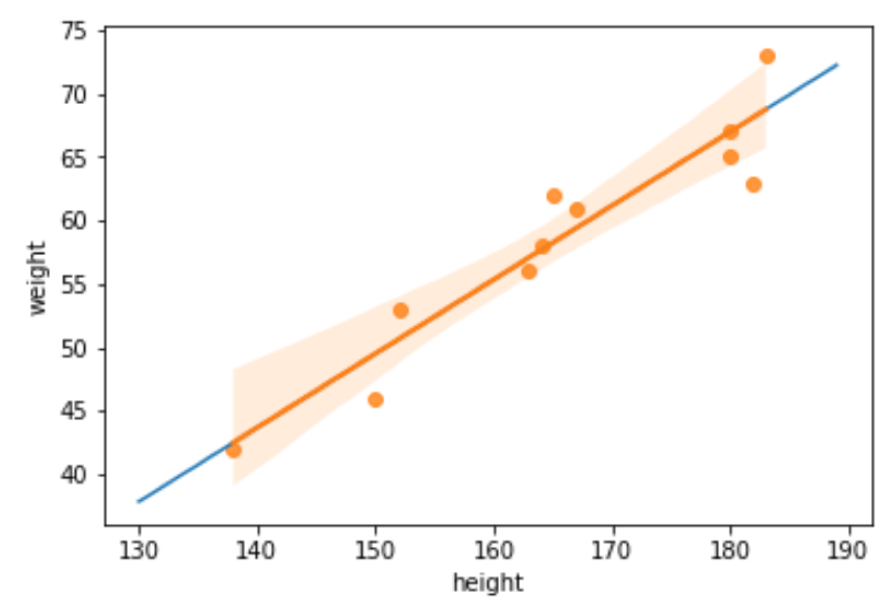
青い線が求めたaとbを使って描画した線で,オレンジの線がseabornの regplot() を使って描画した線です.ぴったりと重なっていることがわかると思います.つまり,seabornのregplotは内部で線形回帰のアルゴリズムを走らせて描画してくれてるんですね◎
さて,この回帰直線があると何が嬉しいんでしたっけ??
そうです,ある身長の値に対して,体重の予測値を計算することができるんでしたね!
これは先ほどの LinearRegression() の学習済み( .fit() 済み)インスタンス( reg )の .predict() 関数を使うことによって求めることができます.
|
1 2 3 |
X = np.array([[175]]) y = reg.predict(X) print(X, y) |
ここでも X という行列を作成して .predict() しましょう. X はshapeが(サンプル数,特徴量数)なので,例えば今回のように一つの身長に対して予測したければshape=(1, 1)のndarrayを作ればOKです.
この辺りはsklearnで使える他の機械学習のアルゴリズムも同じようにして使うことができます.(これがオブジェクト指向のいいところ)
詳しくは改めて機械学習編で扱っていきたいと思います!
まとめ
またまた長くなってしまいました,,,,統計学のブログはやはり言葉の数が増えがちなので大変です.以下まとめです.
- 回帰直線\(y=a+bx\)の\(a\)と\(b\)は,\(a=\bar{y}-b\bar{x}\)および\(b=r\frac{s_y}{s_x}\)となる
- 数式の導出よりもこの式がなにを意味しているかをイメージできることが重要
- 回帰直線はxとyの平均\((\bar{x}, \bar{y})\)を通る傾き\(r\frac{s_y}{s_x}\)の直線
- 回帰直線\(y=a+bx\)の\(b\)のことを回帰係数と呼ぶ
- Pythonで回帰直線を作るには sklearn.linear_model.LinearRegression() を使う
- グラフに描画するだけなら seaborn.regplot() が便利
こんな感じですね!
長くなってしまいましたが,今回の記事はいずれも超重要な事ばかりを扱いました.sklearnは今後データサイエンスをする上で欠かせないライブラリなので,是非抑えておきましょう!
また,線形回帰はデータサイエンスの基本中の基本です.他にも回帰のアルゴリズムってたくさんあるんですが,その基本となるのがこの線形回帰と最小2乗法です.しっかり押さえて次に進みましょう
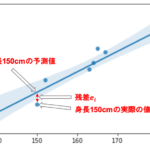
今回は「身長から体重を予測する回帰直線」を作ってみましたが,これって「体重から身長を予測する」にも使えるのでしょうか?
結論からいうと,この二つは異なる回帰直線になり,今回の回帰直線は身長の予測には使えません.
次回はこのあたりを説明し,それから決定係数という超超重要な指標について解説していきます!
それでは!
(追記)次回記事書きました!