正規分布の正体を暴く【統計学入門22】

こんにちは，米国データサイエンティストのかめ(@usdatascientist)です．

Pythonで学ぶデータサイエンス入門：統計編第22回です!

（追記）全16時間の統計学動画講座を公開しました！☆4.8の超高評価をいただいている講座です．こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください．

今までの記事で色々な確率分布をみてきました．

第19回で紹介した最も基本的な二項分布からはじめ，n=1のときのベルヌーイ分布，二項分布の極限として定義されるポワソン分布(第20回)，”成功した回数”ではなく”成功までの待ち時間”を分布にした幾何分布と指数分布(前回)を紹介しました．

今回は

正規分布

を紹介します．

え，今さら？？

って感じですが，今回の記事では正規分布とは一体なんなのかちゃんと解説したいと思います．

正規分布の正体

今までの講座の記事(こことかこことか)でも何度もでてきている正規分布ですが，きちんと正規分布を解説してきませんでした．

ついに，その時がやってきました〜〜〜！！

ってことで今回は正規分布の正体を暴いて(?)いこうと思います！

こちらの記事でも少し触れましたが，正規分布は二項分布の極限で表されます．

もうね，どんな確率分布も「二項分布から」始まるのです．これが二項分布が“確率分布の祖”と言っていた所以です．

二項分布をおさらい

二項分布とはどういう確率分布だったか，もう一度おさらいしてみましょう．(第19回にて詳しく説明してます．)

ある事象が起こる確率$p$の試行を$n$回実施してその事象が$x$回おこる確率を$P(x)$とすると，以下のようにあらわされて，この確率分布を二項分布というのでした．

$$P(x)=_nC_xp^xq^{n-x}=\frac{n!}{x!(n-x)!}p^xq^{n-x}$$

で，この$\mu=np$を一定にして，$n$を無限大に，$p$を0に極限をとった確率分布がポワソン分布と呼ばれる分布になる(近似する)んでしたね．(第21回参照)

この時，$p$を小さくしないケースが正規分布になります(近似します．)

Pythonを使って二項分布が正規分布に近似する様子をみてみよう

第19回と第20回で紹介したPythonのコードを使って，二項分布のグラフを描画してみましょう．

サイコロの例で考えましょう．確率$p$は$\frac{1}{6}$として，$n$の値を変えてみてください．

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from scipy.stats import binom
n = 5 #->50
p = 1/6
x = np.arange(n + 1)
y = binom.pmf(k=x, p=p, n=n)
plt.plot(x, y)
plt.xlabel("Num. of success")
plt.ylabel("probability")

import numpy as np

import matplotlib.pyplot as plt

%matplotlib inline

from scipy.stats import binom

n = 5 #->50

p = 1/6

x = np.arange(n + 1)

y = binom.pmf(k=x, p=p, n=n)

plt.plot(x, y)

plt.xlabel("Num. of success")

plt.ylabel("probability")

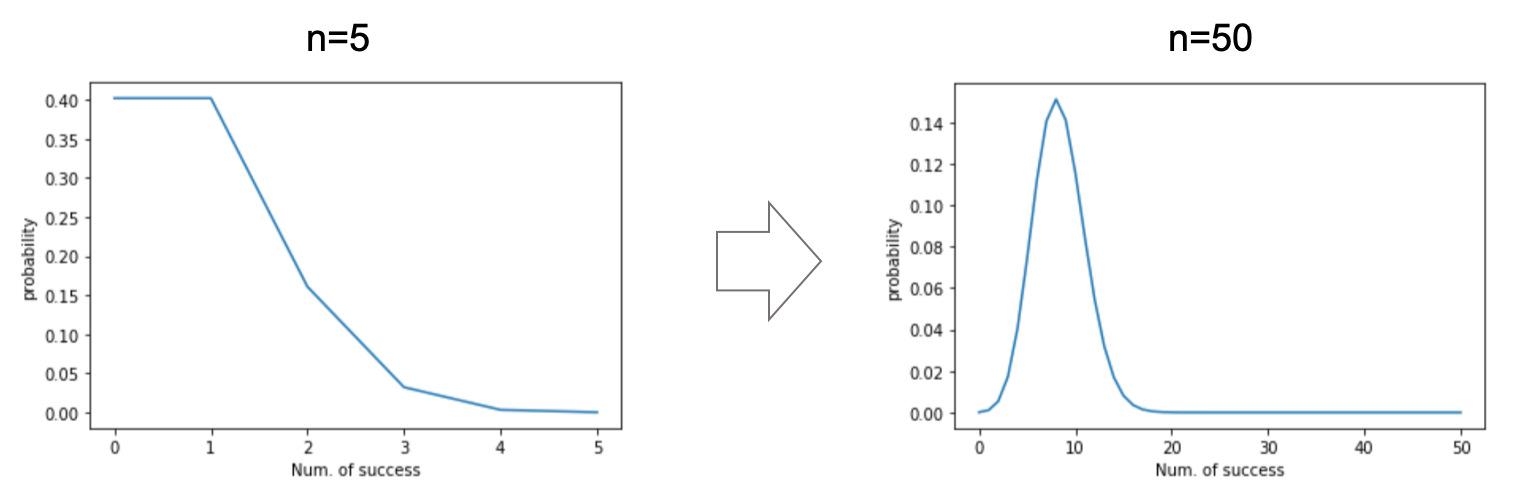
例えば n=5 の時と n=50 の時で比べてみてください．だんだんと正規分布っぽくなっているのがわかると思います．
(わかりやすくするために各点を線で結んでいますが，二項分布は離散確率分布なので実際には飛び飛びの値をとるので注意してください．)

さて，証明は省きますが，正規分布の確率密度関数$f(x)$は以下の数式で表されます．(覚える必要はないですが，あまりにも有名なので統計学を勉強してると見慣れます．)

$$f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$$

この式で重要な点は，「正規分布の形は平均$\mu$と分散$\sigma^2$で完全に決まる」ということです．パラメータがその二つしかないんですね．

そしてこの平均$\mu$と分散$\sigma^2$はそれぞれ二項分布の$np$および$npq$になることがわかっています．

平均$\mu$が$np$になるのはわかると思います．例えば「サイコロを100回投げるので2の目が出る回数を当ててください」って言われたら単純に$100\times\frac{1}{6}$が一番可能性が高いのでそう答えますよね？（正規分布は平均が一番ピーク(確率密度最大)です．）

分散$\sigma^2$については直感的にイメージするのは難しいですが，$n$が大きくなれば当然$x$のばらつきも上がるのはイメージできるのではないかと思います．

これらは覚える必要はないですが，二項分布のパラメータを使って正規分布を描けることを知っておきましょう(そしたらあとはググれば理解できますからね)

Pythonで正規分布のカーブを描く

NumPyを使って正規分布から値を生成する関数はこちらの記事でやりました．

今回は scipy.stats の norm.pdf() を使って正規分布を描画してみましょう．( .pdf() については前回の記事でも扱ってます．)

from scipy.stats import norm
n = 50
mu = n * p
std = np.sqrt(n * p * (1-p))
x = np.arange(n + 1)
y = norm.pdf(x=x, loc=mu, scale=std)
plt.plot(x, y)
plt.xlabel("Num. of success")
plt.ylabel("probability density")