幾何分布と指数分布を解説！ポワソン分布との関係は？【統計学入門21】

こんにちは，米国データサイエンティストのかめ(@usdatascientist)です．

Pythonで学ぶデータサイエンス入門：統計編第21回です!

（追記）全16時間の統計学動画講座を公開しました！☆4.8の超高評価をいただいている講座です．こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください．

前回の記事では，前々回の記事で解説した二項分布という超基本となる確率分布から発展したポワソン分布を解説しました．

ポワソン分布は，実世界の問題にも応用できる実践的な確率分布だったのですが，今回はポワソン分布に引き続き幾何分布と指数分布について扱っていこうと思います．

幾何分布や指数分布は，二項分布やポワソン分布が「回数」に着目していた確率分布だったのに対し，「時間」や「間隔」に着目したもので，どちらもポワソン分布と同じくらい重要な確率分布になるので，しっかり押さえておきましょう！

前回までの記事がしっかりわかっていれば，今回の記事はそこまで理解するのに難しくないと思います．

端的にいうと，

幾何分布は「確率$p$で起こる事象が初めて観察されるまでの試行回数$x$の確率」
指数分布は幾何分布の連続確率分布バージョンで，「ある時間(単位時間)内に平均$\lambda$回起こる事象が次に起こるまで(つまり発生間隔)が$x$単位時間である確率」

をそれぞれ表してた分布になります！

これだけ読んでもいまいちピンと来ないと思うので，きちんと解説していきます！

二項分布は「回数」に着目し，幾何分布は「時間」に着目する

二項分布は，例えばサイコロを3回投げて2の目がでる”回数”に興味がありました．

ポワソン分布も，単位時間あたりに”何回”起きたのかに興味がありました．これらは“成功する回数”に着目していますよね？

幾何分布では，はじめて2の目が出るまでに”試行した回数”に興味があります．これは同じ「回数」という単語ですが，意味合いが違います．幾何分布の場合は，はじめて2の目がでるまでの「待ち時間」と考えるとイメージしやすいと思います．

幾何分布(Geometric distribution)は，はじめて成功するまでの待ち時間の確率分布なので，離散的待ち時間分布なんて呼ばれることもあります．

“時間”という概念を，ここでは「何回試行したか？」という”回数”で表していると考えればOKです．

幾何分布の確率質量関数の式は二項分布の式から簡単に求めることができます．

$n$回の試行で，確率$p$で起こる事象が$x$回起こる二項分布の式は以下のように表せるんでした．(こちらを参考)

$$P(x)=\frac{n!}{x!(n-x)!}p^xq^{n-x}$$

$q$はその事象が起きない確率で$q=1-p$です．

これをもとに，確率$p$で起こる事象がはじめて観察されるまでに試行した回数$x$の確率の式を考えてみましょう．

全試行回数$x$のうち，確率$p$の事象が起こった回数は1回，それ以外(確率$q$)は$x-1$回なので，以下のように表すことができます．

$$P(x)=q^{x-1}p$$

これが幾何分布を表す確率質量関数の式です．

めちゃくちゃシンプルですね．確率$p$の事象が起こるのは必ず最後なので，組み合わせも1個です．

ちなみに，数式はさほど重要ではありません．が，そこまで難しい数式ではないのと，幾何分布がなにかをきちんと理解していれば自然と覚えられるのでは無いでしょうか？

さて，それでは今までの確率分布同様にPythonで幾何分布をplotしてみましょう．

前回の記事で紹介した， .pmf() を使ってplotしてみます．

今回は確率$p=\frac{1}{6}$とし，$x=1, 2,…,10$としたときの確率をplotしてみます．

これはサイコロの例と同じですね．

from scipy.stats import geom
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
x = np.arange(1, 11)
y = geom.pmf(k=x, p=1/6)
plt.plot(x, y, 'bo')
plt.vlines(x, 0, y)
plt.xlabel("Num. of trial")
plt.ylabel("probability")

from scipy.stats import geom

import numpy as np

import matplotlib.pyplot as plt

%matplotlib inline

x = np.arange(1, 11)

y = geom.pmf(k=x, p=1/6)

plt.plot(x, y, 'bo')

plt.vlines(x, 0, y)

plt.xlabel("Num. of trial")

plt.ylabel("probability")

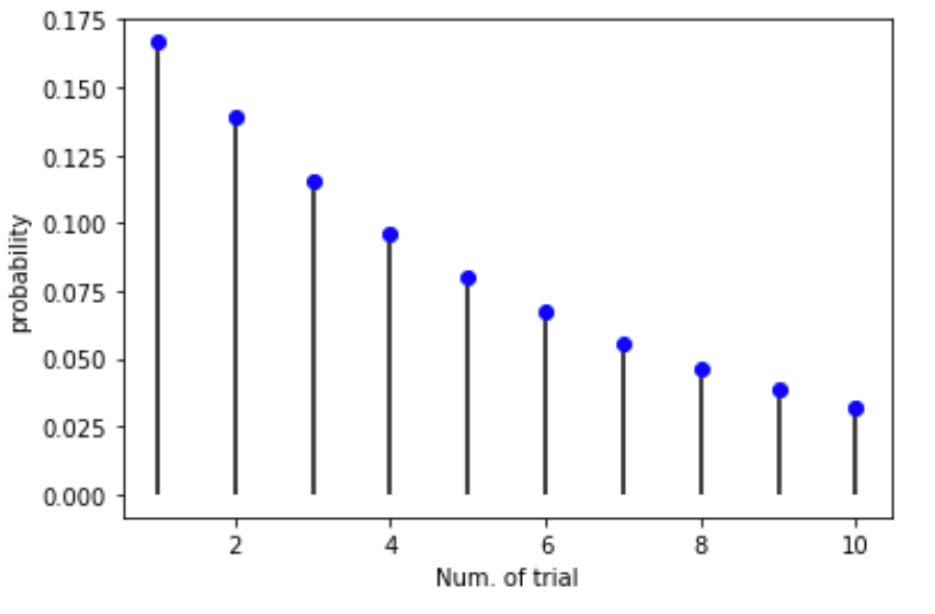
plotの仕方は「データサイエンスのためのPython講座」の第20回を参考にしてください．

結果をみると，$x$が大きくなるにつれ徐々に確率が下がっているのがわかるのと思います．

これは考えてみれば当然．例えば「サイコロを振って初めて2の目が出るまでの試行回数$x$」の例で考えると，サイコロを振る回数を重ねるほど「2の目がまだ一回も出ない」という確率はどんどん下がるはずです．

例えば上のplotで$x=10$の確率というのは，10回目で初めて2の目が出る確率です．これは言い換えると9回連続2の目が出なかったわけです．極端な例ですが，$x=100$の場合，100回サイコロを振って”初めて”2が出る確率です．限りなく0に近いですよね？笑

このように確率が“幾何級数的”に下がるので，幾何分布と呼ばれています．

指数分布は幾何分布の連続バージョン

幾何分布は離散確率分布です．つまり確率変数が取りうる値は離散的(連続ではない)な値になります．1とか2とか20とかです．

これは先のサイコロの例からもわかりますよね？サイコロを投げる回数は離散的な値です．

この幾何分布の連続確率分布バージョンが指数分布(exponential distribution)です．

はて，幾何分布の連続確率分布バージョンとはどういうことでしょうか？

幾何分布では，成功するまでに試行した回数(1回,2回,3回・・・x回)というのが確率変数になっていていました．

指数分布では，成功するまでの時間が確率変数になります．

例えば1時間に平均10回電話がかかってくるコールセンターの場合，次に電話がかかってくるまでの時間が確率変数になります．

導出は飛ばしますが，指数分布の確率密度関数は以下のように表すことができます．

\begin{eqnarray}
P(x)=
\begin{cases}
\lambda e^{-\lambda x}&(x≧0)\\
0&(x<0)
\end{cases}
\end{eqnarray}

$\lambda$はある期間(単位時間)においてその事象が起こる平均の回数です．そして，連続型確率変数$x$がその事象が起こるまでの期間(単位時間)です．

単位時間というのは，例えば1分とか，1時間とかです．例えば１時間に平均10回電話が鳴るコールセンターにおいて，次に電話がなるまで何分かという確率をみたければ，単位時間は「分」で$\lambda$は10/60=1/6となります．

それでは幾何分布と同様に指数分布も scipy.stats を使ってplotしてみましょう．

指数分布は expon を使えばOKです．先ほどのコールセンターの例をplotしてみます．

from scipy.stats import expon
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
x = np.arange(-10, 100)
y = expon.pdf(x=x, scale=6)
plt.plot(x, y)
plt.xlabel("Time[min]")
plt.ylabel("probability density")

from scipy.stats import expon

import numpy as np

import matplotlib.pyplot as plt

%matplotlib inline

x = np.arange(-10, 100)

y = expon.pdf(x=x, scale=6)

plt.plot(x, y)

plt.xlabel("Time[min]")

plt.ylabel("probability density")

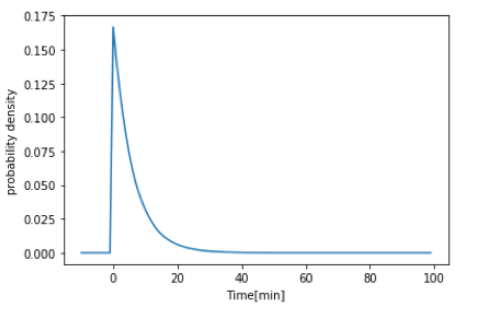
幾何分布の geom と違って，指数分布の expon は連続確率分布なので， .pmf() ではなくて .pdf() を使っていることに注意しましょう．(PMFはProbability Mass Function, PDFはProbability Desnity Functionで，それぞれ確率質量関数と確率密度関数)

パラメータ$\lambda$は， .pmf() の scale という引数を使います．scale引数には$\frac{1}{\lambda}$を入れます．なので今回の場合$\lambda=\frac{1}{6}$なので scale には6を入れます．

今回単位時間は分にしているので，横軸は時間[分]で，このplotは1時間に平均10回鳴るコールセンターにおいて$x$分後に次の電話が鳴る確率を表しています．

$x$が負である確率は0になっていますね．これは当然です．

次に電話が鳴る時間が長くなるほどその確率は下がっていきます．当然1時間に平均10回も鳴るのに，30分経っても電話が鳴らないなんてことは滅多に起きなそうですよね．