決定係数R2で回帰式の精度を評価する【統計学入門17】

Pythonで学ぶデータサイエンス入門：統計編第17回です．

（追記）全16時間の統計学動画講座を公開しました！☆4.8の超高評価をいただいている講座です．こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください．

前回の記事で決定係数\(R^2\)を紹介しました．

決定係数\(R^2\)は「説明変数\(x\)がどれだけ目的変数\(y\)を説明しているのかを表す指標」と説明しましたが，

決定係数\(R^2\)の定義式だけをみるとまさにこの説明が的確なんですが，実際に決定係数\(R^2\)を業務で使う場合って，十中八九，回帰式の精度を示す指標として使われます．

なぜ決定係数\(R^2\)が回帰式の精度の指標として使えるのでしょうか？今回はこの辺りを解説したいと思います．

前回の記事の内容がきちんとわかっていれば簡単に理解できるはずなので，もし前回の記事を読んでない人は先にこちらに目を通しておいてください！

【Pythonで学ぶ】決定係数R2を超わかりやすく解説【データサイエンス入門:統計編16】

決定係数は「回帰の当てはまりの良さ」を表している

まず，以下の二つの図を見比べてください．

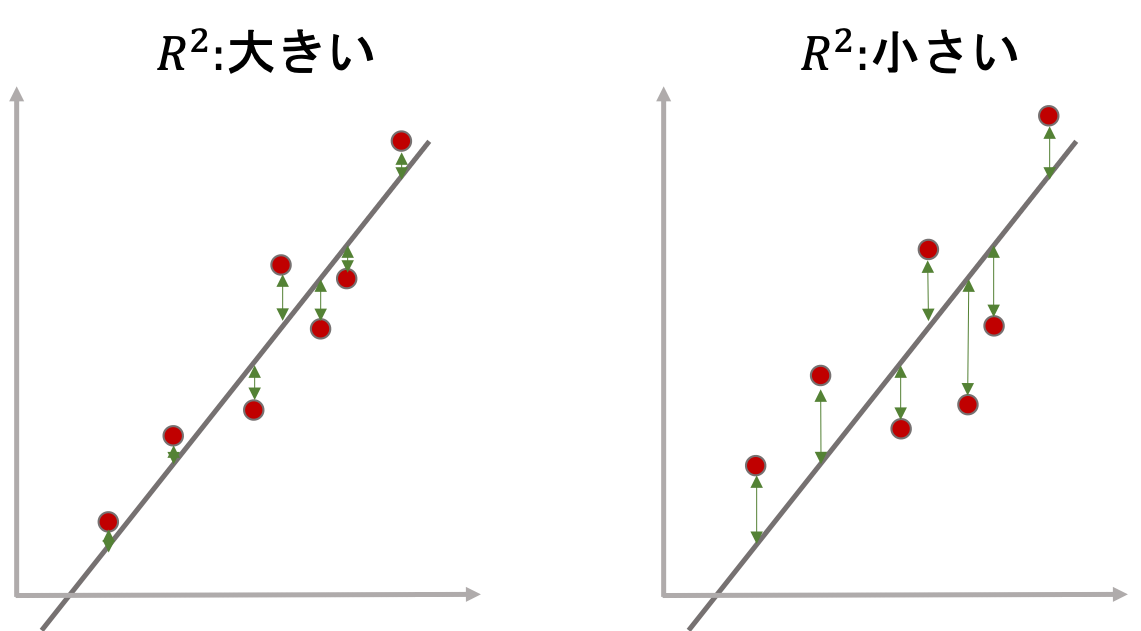
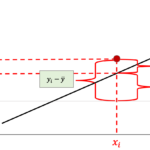
左の回帰直線は，右の回帰直線に比べて各データの回帰直線からの差が小さいです．これはつまり，前回の記事で解説した決定係数\(R^2\)の式の\(y_i-\bar{y}_{x_i}\)が小さくなることを意味していて，つまりは\(s_{y\cdot x}\)が小さいことを意味します．

$$s_{y\cdot x}=\frac{1}{n}\sum^{n}_{i=1}{(y_i-\bar{y}_{x_i})^2}$$

$$R^2=\frac{s_y^2-s_{y\cdot x}^2}{s_y^2}=1-\frac{s_{y\cdot x}^2}{s_y^2}$$

\(s_{y\cdot x}\)が小さくなるということは，\(y\)のうち\(x\)で説明できない部分が小さいということなので，上の\(R^2\)の定義式からもわかるとおり，\(y\)の多くが\(x\)で説明できる，つまりは決定係数\(R^2\)が大きくなるということです．

もう一度上の二つのグラフを見比べてみましょう．左は右に比べて「回帰直線がデータによく当てはまっている」と思います．

「回帰直線がデータによく当てはまっている」と「決定係数\(R^2\)は高くなる」のです．ということは，決定係数\(R^2\)が回帰式の当てはまりの良さに使用することができるということです．

この「回帰直線がデータにどれだけ当てはまっているか」が，「回帰直線がどれだけ正しく予測できいるか」を表しているのはおわかりいただけると思います．

しかし，回帰直線を引くのに使ったデータに対しての当てはまりの良さをみても，意味がないですよね？

そう，決定係数\(R^2\)で回帰直線を評価する場合，未知のデータに対してどれだけ回帰直線が当てはまっているかを評価します．

学習データと評価データ

少し機械学習の話をしましょう．この辺りはまた機械学習編で詳しく解説しますが，一般に機械学習をして予測モデルを構築する際に，その予測モデルを構築(学習)するのに使用したデータを「学習データ」といい，評価に使用するデータ(学習に使っていないデータ)を「評価データ」といいます．(そのままですねw)

• 学習データ：予測モデルの学習時に使用
• 評価データ：予測モデルの学習時には使用せず，精度を測る際に使用する

学習データは学習時にすでに使っているので，そのデータで作った予測モデルは，それらのデータに対して精度が高く出てしまう可能性が高いです．

予測モデルの精度は，「未知のデータをどれくらい正確に予測できるか」を測る必要があるので，学習に使っていないデータを評価データとして用意して，それを使って精度を測ります．

詳しくは機械学習編で改めて解説したいと思います．

なので，決定係数\(R^2\)で回帰直線を評価する際は，学習データとの当てはまりではなく，評価データとの当てはまりの良さをみます．

評価データで決定係数を算出する

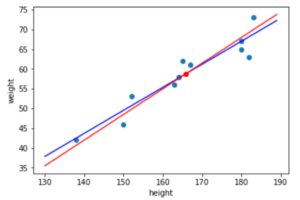
さて，ある回帰直線を学習データから算出(学習)し，その回帰直線が評価データにどれくらいフィットするかを決定係数を計算して評価してみましょう．

全体の流れは以下のようになります．

1. 学習データを使って回帰モデルを学習する(つまり，回帰直線を算出する)
2. 評価データを使って回帰モデルの予測値を計算する
3. 評価データの実際の値と予測値を使って決定係数を算出する

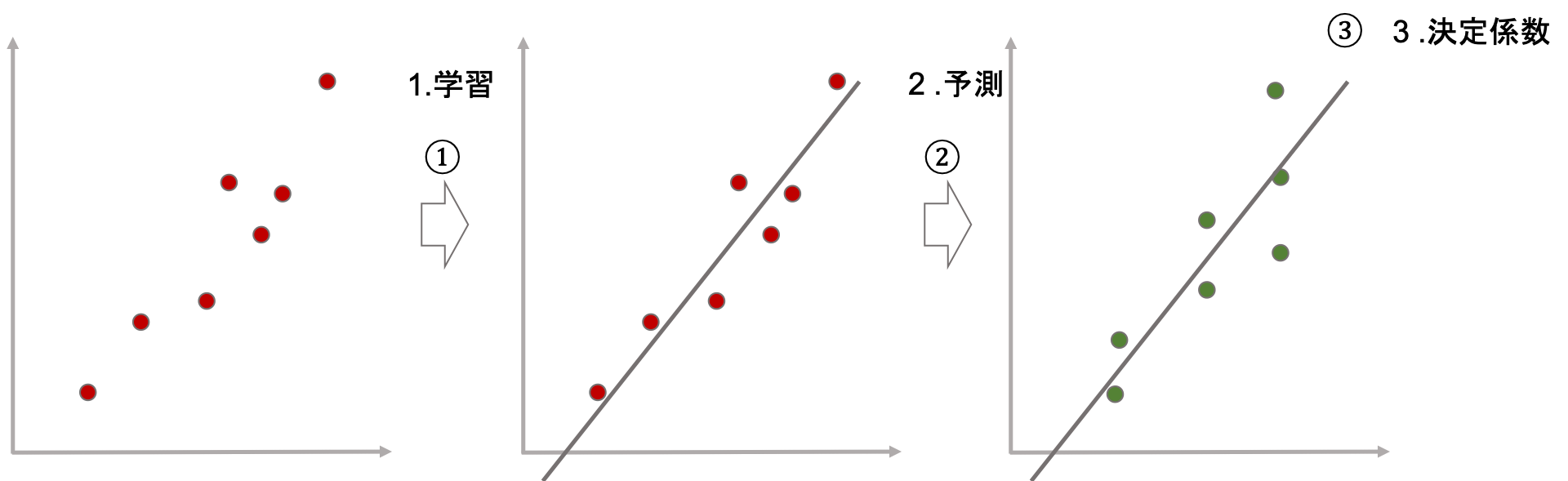
(図の赤い点は学習データで，緑の点が評価データです．)

もう一度決定係数\(R^2\)の式をみてみましょう．

$$s_{y\cdot x}=\frac{1}{n}\sum^{n}_{i=1}{(y_i-\bar{y}_{x_i})^2}$$

$$s_y^2=\frac{1}{n}\sum^{n}_{i=1}{(y_i-\bar{y})^2}$$

$$R^2=\frac{s_y^2-s_{y\cdot x}^2}{s_y^2}=1-\frac{s_{y\cdot x}^2}{s_y^2}$$

これは，以下のように書き換えることができますね．

$$R^2=1-\frac{\sum^{n}_{i=1}{(y_i-\bar{y}_{x_i})^2}}{\sum^{n}_{i=1}{(y_i-\bar{y})^2}}$$

\(\bar{y}_{x_i}\)は回帰式\(y=a+bx_i\)によって計算される値であり，これは本記事で説明してきた「予測値」であると言えます．

ここで，回帰式によって計算された予測値を\(\hat{y}\)とし，実際の評価データの値を\(y_i\), その平均値を\(\bar{y}\)とすると，決定係数\(R^2\)は以下のように書き換えることができます．

$$R^2=1-\frac{\sum^{n}_{i=1}{(y_i-\hat{y}_i)^2}}{\sum^{n}_{i=1}{(y_i-\bar{y})^2}}$$

この数式は，前回の記事で紹介した数式と同じ意味ですが，「回帰式の評価指標としての決定係数」としてこの式がよく使われます．この式もよく見ると思いますので見慣れておくといいと思います！

んー，なんだか数式ばかりでよくわかんなくなってきた・・・(汗

という方のために，次はPythonで実際に決定係数を求めてみたいと思います．

統計学の本で理論を勉強してる時はなかなか理解ができなかったり腑に落ちないことが多いと思います．自分もそうでした．．

そういう時はコードを書いて，実際に自分で実装してみるのがいいです．自分で順序立ててコードを書いていくと理解できるものです．

Pythonで決定係数を計算する

Pythonで決定係数を求めるには，scikit-learnの metrics モジュールの r2_score() 関数を使います．

scikit-larnは機械学習用のライブラリだという話はなんどか本ブログで話している通りです．

metricsというのは，評価基準とか指標という意味です．機械学習のモデルの評価に使う多くの関数が metrics モジュールに入っています．

決定係数が回帰モデルの評価指標に使われることがわかれば，決定係数を求める関数が，scikit-learnの metrics モジュールにあることがすんなりと理解できると思います．

それでは，先ほどの以下の3つのステップをコーディングしてみましょう！

1. 学習データを使って回帰モデルを学習する(つまり，回帰直線を算出する)
2. 評価データを使って回帰モデルの予測値を計算する
3. 評価データの実際の値と予測値を使って決定係数を算出する

今回は学習データと評価データはダミーのデータを使います．他によくやるやり方としては，例えばあるデータの80%を学習データに，20%を評価データにしたりするんですが，その辺りのお作法は機械学習編できちんと紹介します．

いつもどおり，身長から体重を予測する回帰モデルを作るので，身長\(x\)( height )と体重\(y\)( weight )のデータを使います．

1.学習データを使って回帰モデルを学習する(つまり，回帰直線を算出する)

これは以前こちらの記事で詳しく解説しているので，解説は飛ばします．

2.評価データを使って回帰モデルの予測値を計算する

今回は評価データ( weight_test , height_test )を適当に作りました．

学習済みのモデルから予測値を求めるには .predict() 関数を使えばOKです．(こちらの記事でもやりました．)

3. 評価データの実際の値と予測値を使って決定係数を算出する

それではいよいよ決定係数を計算しましょう．

今回は「評価データ」と「その予測値」を使うことに注意してください．(学習データは使いません．)

決定係数はscikit-learnの metrics モジュールの r2_score() 関数を使います．

簡単ですね♪

興味がある人は第15回の記事を参考にしてvisualizationもしてみてください！

決定係数の値に対する明確な基準はありませんが，感覚的には

• 0.6未満:正しく予測できているとは言い難い
• 0.6~0.8:現実的な数値
• 0.8~0.9:精度が高い印象
• 0.9~:過学習の可能性あり

という感じでしょうか．

まとめ

今回は回帰モデルの評価指標としての決定係数について解説しました！

業務で決定係数を使うケースのほとんどが回帰モデルの評価指標として使うケースだと思います．

ですが，これは前回の記事で解説した「説明変数\(x\)がどれだけ目的変数\(y\)を説明しているのか」と考え方は同じで，対象となるデータが評価データになるという点に注意しましょう．

• 決定係数\(R^2\)は回帰モデルの評価指標として使うことができる
• 決定係数\(R^2\)は回帰モデルの評価データに対する当てはまりの良さの指標
• scikit-learnの metrics モジュールの r2_score() 関数を使って決定係数を求めることができる

今回の記事で，統計的記述の範囲は以上です！

次回以降は後半編に入っていきます！後半編は統計学の真髄とも言える推測統計の分野です！

「統計学」って言ったら普通は「推測統計」を指します．なので統計学講座の真骨頂ともいえる内容になっていきますので，是非後半編も進めていってください！

それでは！

追記)次回の記事書きました！後半戦も頑張っていきましょう〜！

絶対にわかる確率変数と確率分布と確率密度【統計学入門18】