不偏分散ってなに？？なぜ標本分散は母集団分散より小さくなるのか【統計学入門⑥】

こんにちは，米国データサイエンティストのかめ(@usdatascientist)です．

前回の記事で，散布度の指標として最も重要な分散$s^2$と標準偏差$s$を解説しました．NumPyとscipy.statsやPandasを使って，Pythonで分散と標準偏差を求めましたね．

scipy.statsとPandasで計算した結果がNumPyと計算した分散と異なっていました．これは，scipy.statsやPandasで計算される分散は不偏分散と呼ばれるものだからです．

不偏分散というのは，分散の式で$n$で割っているところが$n-1$になる．という話まで前回の記事でしましたね．

今回はこの(急に出てきた，謎の)不偏分散とは一体なんなのかを超わかりやすく解説します！！

結論からいうと，

不偏分散は，標本データから母集団の分散を推定するのに使う指標である
↑が理解できると，NumPyが不偏分散を使っていない理由はNumPyはただ単に引数に取ったデータの分散の記述的指標を計算しているだけだということがわかる
一方でscipy.statsやPandasは統計やデータサイエンスで使われることを想定しているので不偏分散を返す
不偏分散の方が統計学の理論を構成する上で普通の分散よりも使い勝手がいいこともあって，デフォルトでは不偏分散を返すツールやライブラリが多い

といった感じです．

それでは詳しく解説していきます．

（追記）全16時間の統計学動画講座を公開しました！☆4.8の超高評価をいただいている講座です．こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください．

母集団の分散を推定するにはどうすればいいか

第一回でお話しした通り，統計学のメインは「母集団の特性を，限られた標本データを使って推測する」こと，つまりは推測統計です．

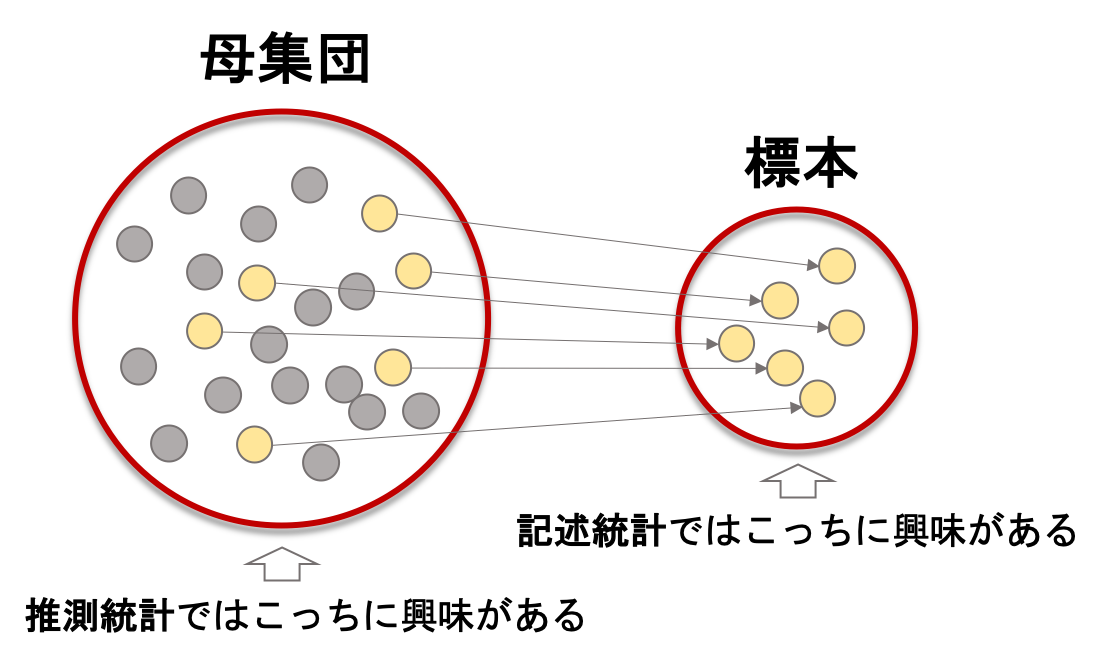
今までの記事で解説してきたのは，記述統計の方です．記述統計では「今手元にあるデータの特性」を記述することを考えていました．

この違いを(統計学を学ぶ上では)明確に分けておきましょう．

またあとで詳しくやりますが，母集団の指標を推測するのに標本の指標を使います．例えば，標本の「平均」は母集団の「平均」を推測するのに使えることがわかっています．(詳しくは本講座でまた説明します．)

つまり，一言に「平均」と言っても，記述統計の文脈と推測統計の文脈では意味合いが異なるんですね．単に「標本データの」平均を言っているのか，それとも「標本データのうしろにある大きなデータ(母集団)の」平均を推測した値を言っているのかは，意味合いが異なりますよね？

このように，母集団の特性値を推測するために使われる標本の値を統計量と言い，推定に使う統計量を推定量と言います．(単語は別に覚えなくていいと思います．実業務でちゃんと区別して会話する必要があるケースはそんなに多くないはず．統計学を学ぶ上で名前をつけておくと役に立つので，本ブログでは単語を紹介して，これらを使っていきます．)

つまり，標本で求めた「平均」は母集団の平均値を推定するのに使う推定量なわけですね！

じゃぁ，母集団の分散を推定するのに使える統計量はなんなのか？標本の分散を推定量として使えないのか？

実は，標本の分散は母集団の分散より少し小さくなる傾向があります．まずは，それを感覚的に理解しましょう！

【イメージで理解する】標本の分散はなぜ母集団の分散より小さくなる傾向があるか

これはよーーーく考えれば当たり前のことです．

母集団からランダムに標本を取ってきた場合，標本は母集団の一部です．母集団の範囲を超えて値を取ってくるわけでは無いので，母集団よりもばらつきが小さくなりやすいのは当然のこと．

例えば以下のようなコードを実行してみましょう．

population = np.array([1, 5, 10, 11, 14, 15, 15, 16, 18, 18, 19, 20, 25, 30])
# ランダムに値を抽出
samples = np.random.choice(population, size=3)
print('population variance is {}'.format(np.var(population)))
print('sample variance is {}'.format(np.var(samples)))
print('samples: {}'.format(samples))

population = np.array([1, 5, 10, 11, 14, 15, 15, 16, 18, 18, 19, 20, 25, 30])

# ランダムに値を抽出

samples = np.random.choice(population, size=3)

print('population variance is {}'.format(np.var(population)))

print('sample variance is {}'.format(np.var(samples)))

print('samples: {}'.format(samples))

np.var() で population (母集団)( [1, 5, 10, 11, 14, 15, 15, 16, 18, 18, 19, 20, 25, 30] )の分散と samples (標本)の分散を計算しています．

何度かコードを実行してみてください．多くのケースで標本の分散が母集団の分散の 51.39 を下回るのではないでしょうか？

極端な値の組み合わせ(例えば [1, 5, 30] や [1, 25, 30] )を取らない限りは大抵母集団の分散を下回ります．これは，ランダムで標本を抽出するので，標本の分布は母集団の分布の偏りに応じて出てきやすい値があったり，逆に分布から外れた値は標本に入ってくる確率が減るので，必然的に散らばりが($\frac{n-1}{n}$だけ)小さくなる傾向にあります．

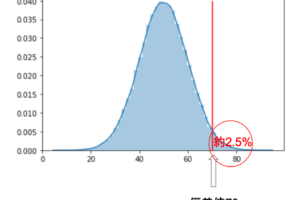
イメージですが，こんな感じでしょうか↓

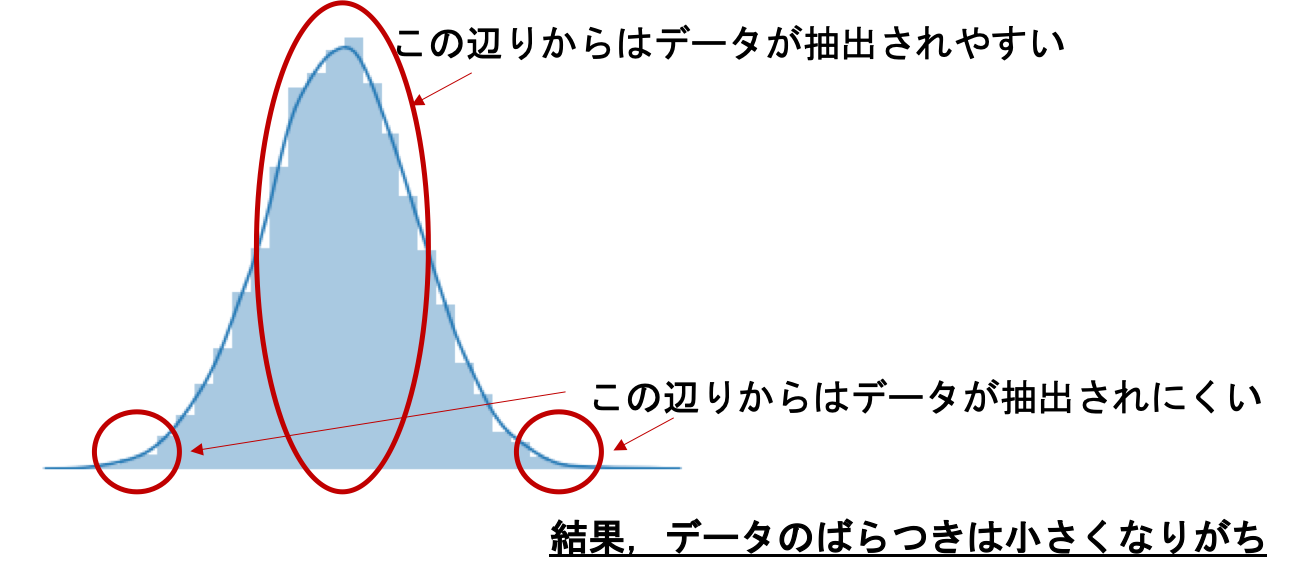
ちなみにこの図は以下のようにして描画することができます．

import seaborn as sns 
sns.distplot(np.random.randn(int(1e4)), bins=30)
plt.axis('off')

import seaborn as sns

sns.distplot(np.random.randn(int(1e4)), bins=30)

plt.axis('off')

(seabornはデータサイエンス必須のPythonライブラリです．distplotについてはこちらに記事を書いています．また，動画講座でかなり詳しく説明しているのでまだ受講されていないかたは是非受講してください！)

これで「標本の分散は母集団の分散より小さくなりがち」のイメージがわかったのではないかと思います．標本の数($n$)が小さければそれだけ分布から外れた値が標本に含まれる確率が減るので，分散が小さくなることもイメージできると思います．

【もう少し数学的に理解する】標本の分散はなぜ母集団の分散より小さくなる傾向があるか

もう少し数学的に理解してみましょう．

母集団の特性値をギリシャ文字で表すことが多いので，本講座では母集団の平均値を$\mu$(ミュー)，分散を$\sigma^2$(シグマ2乗)で表すこととします．

そうすると，さきほどPythonのコードで計算した母集団の分散$\sigma^2$と標本の分散$s^2$は以下のような数式になると思います．(こんな数式わかりません！という人は前回の記事を見返してくださいね)

$$\sigma^2=\frac{1}{n}\sum_{i=1}^{n}{(x_i-\mu)^2}$$

$$s^2=\frac{1}{n}\sum_{i=1}^{n}{(x_i-\bar{x})^2}$$

両者を見比べてみると，(当然ですが)母集団の分散$\sigma^2$の計算には母集団の平均$\mu$を，標本の分散$s^2$には標本の平均$\bar{x}$を使っているのがわかると思います．

しかし，標本の分散を求める際に使う平均値って，標本の平均$\bar{x}$でいいのでしょうか？本来であれば母集団の平均$\mu$を使うべきではないでしょうか？

$$s^2=\frac{1}{n}\sum_{i=1}^{n}{(x_i-\mu)^2}$$

もし「母集団の分散の推定値」として標本の分散を計算するのであれば，母集団の平均$\mu$を使った方が本当の母集団の分散$\sigma^2$に近い値が計算されそうですよね？

でも，母集団の平均$\mu$は通常分からないので使いたくても使えません．そこで，母集団の平均$\mu$の推定量である標本の平均$\bar{x}$を代わりに使っているんですね！(標本平均を母集団平均の推定量として使えるということは本記事の前半で話した通りです)

ここで，「算術平均は，各値からの差の平方和の合計を最小にする値」という算術平均の重要な性質を思い出しましょう．(こちらで出てきましたね！)

つまり，標本においてある値$X$からの差の2乗の合計(平方和)を最小にする$X$は標本平均$\bar{x}$になるということです．

$\sum_{i=1}^{n}{(x_i-X)^2}$($X=\bar{x}$の時最小)

つまり，

$$s^2=\frac{1}{n}\sum_{i=1}^{n}{(x_i-\bar{x})^2}$$

において，もし標本平均$\bar{x}$ではなく他の値が使われていたら，$s^2$はもっと大きい値になるということです．

そう，もし標本平均$\bar{x}$じゃなく母集団の平均$\mu$を使ってもです．つまり

$$\frac{1}{n}\sum_{i=1}^{n}{(x_i-\bar{x})^2}\le\frac{1}{n}\sum_{i=1}^{n}{(x_i-\mu)^2}$$

ということです．本来母集団の平均$\mu$を使って求めたいところ，母集団の平均$\mu$は通常未知なのでその推定量である標本平均$\bar{x}$を使って分散を計算すると，ちょっと値が小さく計算されてしまうというのが理解できるのではないでしょうか？

不偏分散は母集団分散の推定量として使える

ここまできたらもうわかりますよね？標本の分散$s^2$を普通に計算すると，母集団の分散$\sigma^2$より小さくなるので，標本の分散$s^2$は母集団$\sigma^2$の分散の推定量に使うことはできません．標本の分散$s^2$よりも少し大きい値である不偏分散を推定量として使うのです．

つまり，不偏分散というのは，母集団分散$\sigma^2$の推定量なんですね．

なので，scipy.statsやPandasではただ単に分散を求めるのではなくて，より統計学の理論に親和性のある不偏分散を求めていたのでした．

統計学の理論上，不偏分散の方が普通の分散よりも扱いやすい面もあるので，多くの統計ツールでは分散の計算にデフォルトで不偏分散を返すものが多いです．

推定量ではなく，ただ単に標本の分散や標準偏差を記述統計の文脈で使用するのに，普通の分散で計算してようが不偏分散を使ってようが正直あまり気にする人はいないと思いますが，念の為自分が使っているツールやライブラリがどちらを返すのかはみておいた方がいいでしょう．(nが大きければ値の差は小さくなるので，特に大きな標本ではそこまで気にする必要はないと思います)