(追記)全16時間の統計学動画講座を公開しました!☆4.8の超高評価をいただいている講座です.こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください.
過去数回の記事で散布度について紹介をしてきました.(散布度というのはデータのばらつき具合を表す指標です.)
第4回:範囲,IQR(四分位範囲),QD(四分位偏差)
第5回:平均偏差,分散,標準偏差
第6回,第7回:不偏分散
範囲は最大値,最小値を使うので外れ値に弱く,IQR,QDは外れ値には強いですが全てのデータを計算に使うわけではないので信頼度は低い.
そこで考えられたのが平均偏差ですが絶対値の扱いが厄介なので,2乗することにしたのが分散.2乗すると値の尺度が変わるのでそれを直したのが,分散の平方根をとった標準偏差.母集団の分散の推定をする場合は不偏分散.
↑こんなストーリで考えると全部覚えやすいと思いますし,それぞれの特徴もイメージできるでしょう◎
さて,いろいろ散布度を紹介しましたが,一番重要なのは標準偏差です.ほとんどの論文等で散布度を示すのに標準偏差が使われていると思います.
今回は標準偏差が具体的にどれくらいだったらデータのばらつき具合がどうなのかというのを説明したいと思います.
目次
「平均±標準偏差」の間にどれくらいデータが入っているかを考える
「標準偏差が○○だったらデータはこれくらいばらついてる」といのは,「平均から±標準偏差の範囲にこれくらいのデータが入っている」という形で表すことができます.これがわかればデータの分布がなんとなくわかりますよね?
例えば平均50点,標準偏差10点のデータの分布があって,もし,50±10点の間にデータがどれくらいあるかが分かれば,そのデータの散らばる具合がなんとなくですが掴めますよね?
実は,これはデータの分布によって変わるので,あらゆるデータの分布に対して平均±標準偏差内のデータの割合を正しく算出することはできません.
ただ,それだと役に立たないので,ここでは感覚値を伝えておきます.平均を\(\bar{x}\),標準偏差を\(s\)とすると,
\(\bar{x}±s\)の範囲に約\(\frac{2}{3}\)
\(\bar{x}±2s\)の範囲に約95%
\(\bar{x}±3s\)の範囲に約99%~100%
この3種類は頭の片隅に入れておきましょう.これはなにを言っているかというと,例えばクラスで実施したあるテストが平均50点標準偏差10点だった場合,おそらくクラスの67%の人たちは50±10点の範囲にいて,クラスの全員が50±30点に収まるだろう.ということです.
つまり,この場合(平均50点標準偏差10点)は0点も100点もきっといないだろう,というのがわかるわけです.
結構便利ですよね?ただ,これは必ずしも正しいとは限りません.以下のコードで試しにランダムな数字で実験してみましょう.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# 0~1の間でランダムに値をサンプリング randoms = np.random.rand(1000) mean = np.mean(randoms) std = np.std(randoms) # 平均±標準偏差の範囲にいくつ値があるかをカウントする count = 0 coef = 1 thresh = coef * std for num in randoms: if num > mean - thresh and num < mean + thresh: count += 1 print('{}% of the numbers are included within mean±{}std'.format(int(count/len(randoms)*100), coef)) |
|
1 |
57% of the numbers are included within mean±1std |
コードは何も難しいことはしていないので是非自分の手で書いてみてください. np.random.rand(1000) で0~1から1000個の値を生成し,その平均±標準偏差の範囲にどれだけの値があるかをカウントしています.(もっと効率のいい書き方はあると思いますが,今回はわかりやすさを重視しループで回しています. np.random.rand() についてはこちらの記事で解説しています.この辺りを体系的&効率的に学びたい方は動画講座を受講ください.)
ふむふむ,どうやらこのように値がランダムな場合は平均±標準偏差の範囲に入る値の割合は57%になるようですね.
一応グラフも書いてみましょう.seabornやmatplotlibを使って以下のように表示してみます.
|
1 2 3 4 5 6 7 8 9 |
import matplotlib.pyplot as plt import seaborn as sns %matplotlib inline sns.distplot(randoms) plt.vlines(mean, 0, 1, 'r', label='mean') plt.vlines(mean+coef*std, 0, 1, 'b', label='±{}std'.format(coef)) plt.vlines(mean-coef*std, 0, 1, 'b') plt.legend() |
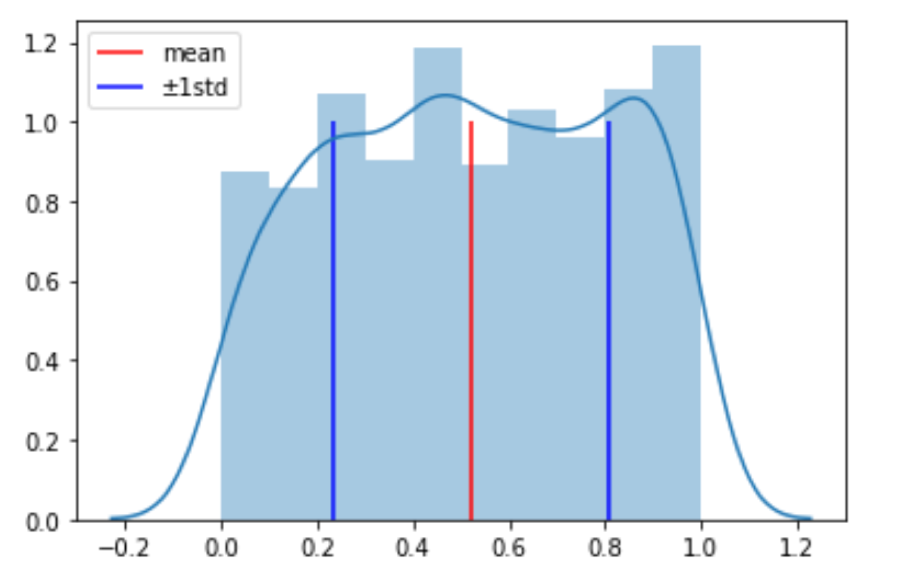
こちらの図で,青の線の間に入るデータの数が57%ということです. coef 変数(標準偏差の”係数(coefficient)”でcoefという名前にしてます)を変えて coef=2 の時, coef=3 の時も試してみてください. coef=2 ですでに全ての値が入ることがわかると思います.これは先ほどの感覚値として挙げた「\(\bar{x}±s\)の範囲に約\(\frac{2}{3}\)や\(\bar{x}±2s\)の範囲に約95%」とは違いますね.
このように,データの分布によってこの感覚値は完全には当てはまらないことを覚えておきましょう.
覚えておくべきは正規分布の場合

そう思ったあなた.まず,第一に「意味なくはない」です.標準偏差を知ることで完璧には把握できないまでも(例えば)「全体のデータが平均±3標準偏差の中に収まる」という感覚は非常に強力です.
そして第二に,たしかに先ほどの例のように完全に感覚値通りにはいかないんですが,統計学では「データの分布が〇〇のように分布していると仮定する」ことが多いです.そして,ほとんどのケースでは“正規分布”と呼ばれる分布を想定します.
(正規分布についてはまた改めてきちんと解説記事を書きますが,簡単にいうと自然界に存在する多くの事象がこの正規分布に従うことから,統計学では最も基本かつ重要な代表的な分布です.)
そうです.前にデータサイエンスのためのPython講座の第9回で紹介した「68-95-99.7ルール」がそれです.
正規分布と呼ばれる分布では,平均±標準偏差の範囲に全体のデータの約68%が,平均±2標準偏差の範囲に全体の約95%が,平均±3標準偏差の範囲には全体の約99.7%がそれぞれ含まれています.
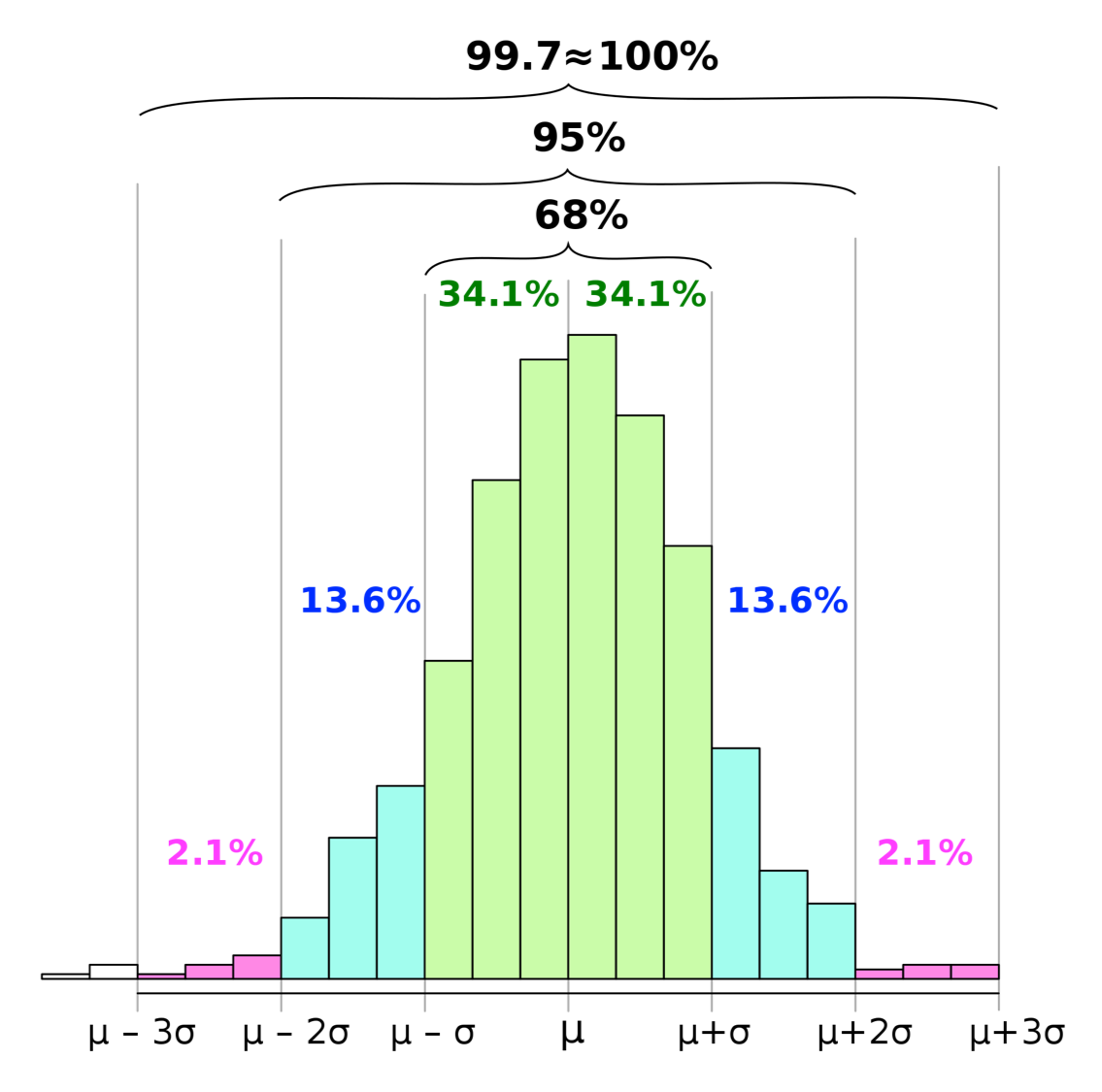
source: wikipedia

やはり細かい数字は覚えなくてもいいと思います.先ほどと同じ感覚で「68%, 95%, ほぼ全部」とそれぞれなんとなく覚えておきましょう!
試しに先程のコードの例で, randoms = np.random.rand(1000) を randoms = np.random.randn(1000) に書き換えて実行してみましょう!0~1の範囲でランダムに値をとる代わりに,平均0, 標準偏差1の正規分布(つまり標準正規分布)から値をランダムに取ってきます.正規分布や標準正規分布についてまた後ほど解説します.
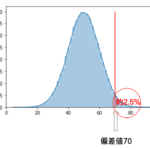
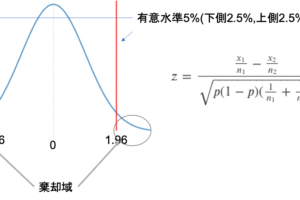
正規分布でちょうど95%の範囲になる平均±1.96標準偏差だけは覚えておくと◎
むしろ,正規分布においてちょうど95%範囲にあたる「平均±1.96標準偏差」の1.96という数字を覚えて欲しいです.

平均±標準偏差はぴったり95%になるわけではないんですね,”約”95%(wikipediaの上図をみると95.4%)なんです.で,手元に標準偏差があって,「データがどれくらい分布してるのかな〜」と思った時には先程の「68-95-99.7ルール」で考えればOKなんですが,データの分布に興味があるわけではないが,「正規分布のどの時点が95%の境目なのか」に興味がある場合が多いです.(今後解説しますが,推定や検定でこのようなロジックを使います.)
そこで,この「1.96」という数字を頻繁に使うので覚えておきましょう!
±1.96以外にもよく使う境目はあるんですが,1つ覚えておけば他の数字は適宜調べればOKです.覚える必要はないと思います.
今の時代,調べられれば勝ちです.ただ,その概念自体を知らないと調べることもできないので,一番よく使う「±1.96」と「95%」を覚えておきましょう!
まとめ
今回は標準偏差を使って,データがどのように分布しているのかがわかりました.これらの情報を使えば,あるデータが全体のデータの中でどれくらいの位置にあるのかがわかりますね.平均値から標準偏差の何倍だけ離れているかを計算することによって検討がつくわけです.これ,結構便利ですよね?
こういう風に使えるというのがわかると,標準偏差にも結構愛着(?)がわきませんか?名前は親近感0ですけど,結構重要なんですよ!
- 一般的には\(\bar{x}±s\)の範囲に約\(\frac{2}{3}\),\(\bar{x}±2s\)の範囲に約95%,\(\bar{x}±3s\)の範囲に約99%~100%のデータが分布する
- これは必ずしも正しいとは限らないが,ある程度の検討をつけることができる
- 正規分布では「68-95-99.7ルール」があることを知っておく.細かい数字までは覚えなくて良い
- ちょうど95%の境目が平均±1.96標準偏差になる.この「1.96」という数字は統計学ではよく出てくるので覚えておく.
統計学ではあまり数字を覚える系はないんですが,「1.96」は数少ない覚えておくべき数字の1つですので是非覚えておきましょう!
さて,今回のように「平均値から標準偏差の何倍だけ離れているか」を計算することができると,もう1つ嬉しいことができます.
それは「平均も標準偏差も異なるようなデータ群で値の比較ができるようになる」ことです!例えばある中学校で実施した英語のテストと,隣の中学校で実施した英語のテストをそのテストの点数だけみて,どちらの成績が良かったかを比較することはできません.が,標準偏差を使いてそれぞれの中学校の中でどの位置にいるかを計算することによって,テストの成績を相対的に比較することができます.(もちろん,それぞれの中学校の全体のレベルが同じではないので完全に比較することはできませんが,,,)
これを応用したのがみなさんご存知「偏差値」です.統計学は結構身近なところで使われているんです.
次回はこのあたりを紹介していきたいと思います!結構実践的な内容なので面白いと思うので是非進めていきましょう.
それでは!
(追記)次回の記事書きました!