データサイエンス入門の機械学習編第10回です!(講座全体の説明と目次はこちら)
追記)機械学習超入門動画講座を公開しました!動画で効率よく学習をしたい人はこちら(現在割引クーポン配布中です)
この講座も第10回まで来ましたが,まだまだ終わる気配はありません笑 機械学習は学ぶこと多すぎですね・・・
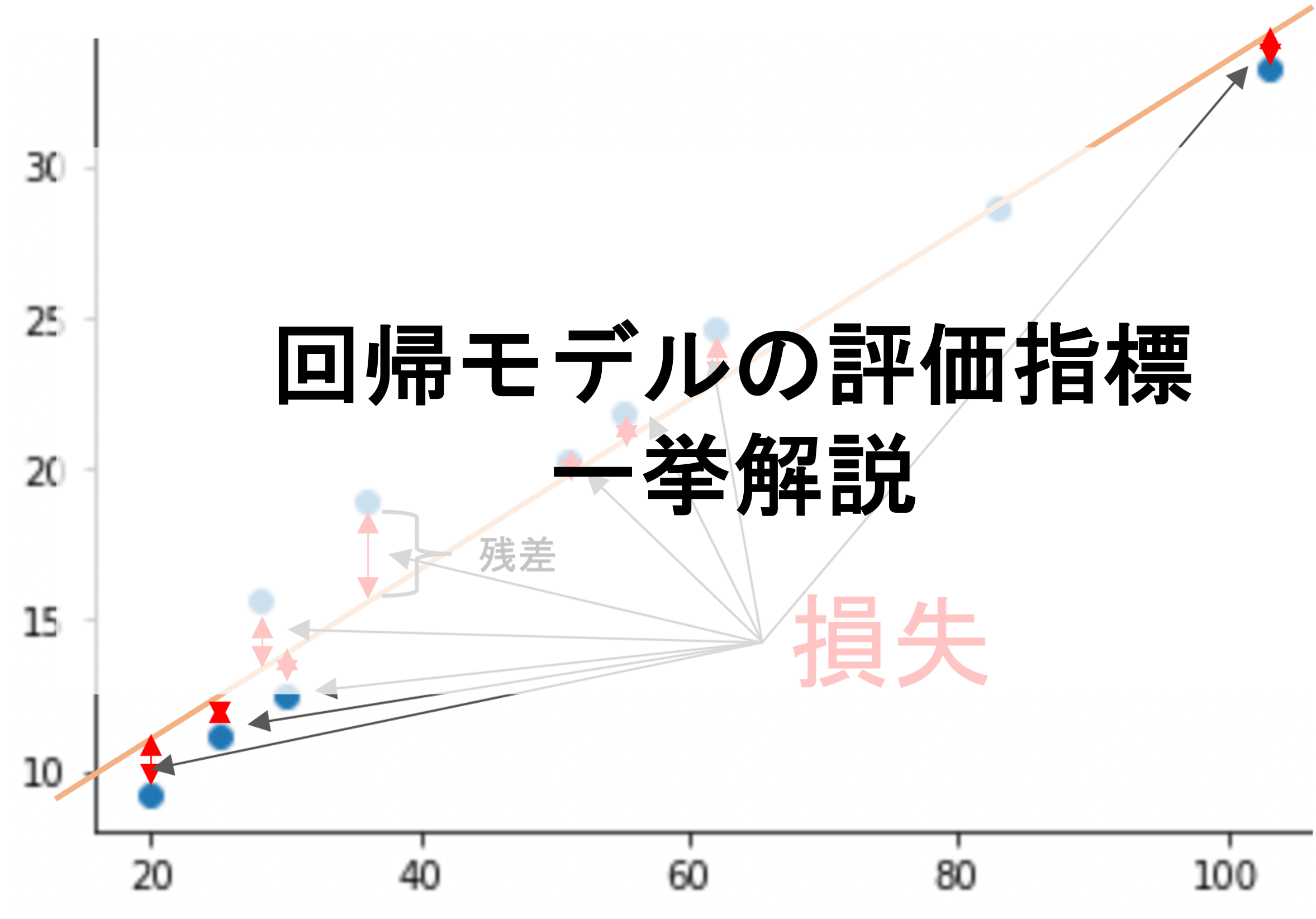
第7回の記事からモデルの汎化性能を測る手法として色々と紹介してきましたが,「そもそもどういう評価指標があるのか?」を今回の記事では紹介していきます.(今回の記事では回帰モデルの評価指標にフォーカスして紹介して行きます.分類器など他のタスクの評価指標についてはまた改めて解説します)
機械学習では,モデルを構築するスキルだけではなく,きちんとモデルを評価できるスキルも求められます.
今回の記事で回帰モデルの一般的に使われる評価指標をしっかり学習していきましょう!scikit-learnを使った簡単な実装法や,それぞれの使い所なんかも解説していきます.
目次
さまざまな回帰モデルの評価指標
機械学習のモデルを構築したら,必ず汎化性能を評価する必要があります.この際評価に用いる指標(metrics)を正しく選択することが非常に重要です.
回帰モデルでよく使われる評価指標は以下です.
1.MSE (Mean Squared Error)
2.RMSE (Root Mean Squared Error)
3.MAE (Mean Absolute Error)
4.R-Squared (\(R^2\))
5.adjusted R-Squared (adjusted \(R^2\))
それではひとつひとつ見ていきましょう
MSE(Mean Squared Error)
これは何度も登場していますね.残差の二乗の平均です.第2回の損失関数の記事でも出てきました.最小二乗法による線形回帰は,学習データのMSEが最小になるようにパラメータを学習しているんでしたね.
$$MSE=\frac{1}{m}\sum^{m}_{i=1}(y_i-\hat{y_i})^2$$
MSEは回帰モデルの評価に最もよく使われる指標だと思います.
しかし,二乗されているので指標の単位がわかりにくいですね.例えばdiamondsデータセットの目的変数であるpriceの単位はドルでした.
MSEの単位はドルの二乗になってしまい,指標の解釈がしづらいという問題点があります.
それを解決するのが次に紹介するRMSEですが,まずはPythonでMSEを計算するやり方を紹介します.
PythonでMSEを計算する
それではPythonでMSEを計算してみましょう!今まではスクラッチでコードを書いていましたが,scikit-learnには簡単にMSEを計算してくれる関数が用意されています.
データは前回の記事同様,tipsデータセットを使います.hold-outで学習データとテストデータをわけ,total_billからtipを予測するモデルを作ってテストデータでMSEを計算します.
MSEの計算には sklearn.metrics.mean_squared_error を使います.評価指標に使う関数は大抵 sklearn.metrics に入っているので覚えておきましょう!
mean_squared_error() に正解データ y_true と予測データ y_pred を入れてあげればOKです!|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
from sklearn.linear_model import LinearRegression from sklearn.metrics import mean_squared_error from sklearn.model_selection import train_test_split import seaborn as sns model = LinearRegression() # data prepare df = sns.load_dataset('tips') X = df['total_bill'].values.reshape(-1, 1) y = df['tip'].values # hold out X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, shuffle=True, random_state=0) # train model.fit(X_train, y_train) # predict y_pred = model.predict(X_test) # evaluate mean_squared_error(y_test, y_pred) |
|
1 |
0.8711845537539947 |
RMSE(Root Mean Squared Error)
RMSE(Root Mean Squared Error)は名前の通り,MSEに平方根をつけたバージョンです.
$$RMSE=\sqrt{\frac{1}{m}\sum^{m}_{i=1}(y_i-\hat{y_i})^2}$$
平方根をつけることにより,指標の単位が目的変数の単位と一致し解釈しやすくなりました.(この辺りは分散と標準偏差の関係に近いですね)
MSEを損失関数として使って,RMSEを評価指標として使うことも多いです.
また,RMSEは残差の二乗の平方根の平均ではないことに注意してください.\(RMSE=\sqrt{MSE}\)です.
PythonでRMSEを計算する
これもMSE同様 sklearn.metrics.mean_squared_error を使います.
mean_squared_error() に squared=False を入れてあとは同じように実行すればOKです.ようはデフォルトでは squared=Trueになっていて二乗した状態なのをなしにする(つまり平方根をつける)ということですね.|
1 |
mean_squared_error(y_test, y_pred, squared=False) |
|
1 |
0.933372676777071 |
MAE(Mean Absolute Error)
MAE(Mean Absolute Error)はその名の通り,残差の絶対値の平均です
$$MAE=\frac{1}{m}\sum^{m}_{i=1}|y_i-\hat{y_i}|$$
MSEやRMSEは残差の二乗を計算していいましたが,これは大きい残差にはそれだけ大きな損失を与える,いわば「罰」のような役割をしていましたが,これによりすこし直感的に解釈するのが難しくなっています.
シンプルに「残差の平均」を確認したいのであればMAEがいいでしょう!
PythonでMAEを計算する
MAEを計算するには sklearn.metrics.mean_absolute_error を使います.使い方は mean_squared_error と同じです
|
1 2 |
from sklearn.metrics import mean_absolute_error mean_absolute_error(y_test, y_pred) |
|
1 |
0.6903119067790223 |
R-Squared
R-Squared(\(R^2\))は統計学第16回で紹介した決定係数\(R^2\)のことです.決定係数\(R^2\)が回帰の精度の指標として使える話は統計学講座第17回でしましたね.この辺りがわからない方は是非上述したリンクの記事をご確認ください!
統計学講座第17回の記事より,\(R^2\)の式は以下のようになります.(導出は統計学講座第17回を参考にしてください)
$$R^2=1-\frac{\sum^{m}_{i=1}{(y_i-\hat{y}_i)^2}}{\sum^{m}_{i=1}{(y_i-\bar{y})^2}}$$
第6回で\(\sum_{i=1}^{m}{(y_i-\hat{y_i})^2}\)をRSS(residual sum of squares)と呼ぶといいましたが,\(\sum^{m}_{i=1}{(y_i-\bar{y})^2}\)のことをTSS(total sum of squares)と呼ぶことも頭の片隅に入れておきましょう.
すると,上記の\(R^2\)は以下のように書き換えることができます.よくこのような表記も用いられるので紹介しておきます.
$$R^2=1-\frac{RSS}{TSS}$$
この式や統計学講座第16回からも,\(R^2\)は\(\mathbf{y}\)のばらつきのうち\(X\)で説明できる割合だということがわかると思います
また\(R^2\)は0から1の値を取る指標で,1に近いほど精度がいいと言えます.MSEなどの損失を計算する指標よりも標準化されるので,わかりやすく,他のモデルとの比較もしやすいです.
PythonでR-Squaredを計算する
\(R^2\)を計算するには sklearn.metrics.r2_score を使います.使い方は mean_squared_error と同じですね!
|
1 2 |
from sklearn.metrics import r2_score r2_score(y_test, y_pred) |
|
1 |
0.49515102188632776 |
total_billとtipにはある程度強い相関があるはずです.実際に相関係数をみると0.68と,そこそこ強めの相関があります.その場合の\(R^2\)が0.5ということで,\(R^2\)が0.5もあれば十分に大きな値であることがわかると思います.
adjuted R-Squared
\(R^2\)は,特徴量を追加すると,たとえその特徴量が目的変数と何ら関係なかったとしても1に近づく性質があります.(これは学習データに対しての\(R^2\)のみです.テストデータの場合はそうとは限りません)
これは,特徴量を追加するだけでRSSが向上,つまり\(\hat{y_i}\)が\(y_i\)に近づくからです.目的変数に関係がある特徴量を増やすことによって\(R^2\)が1に近づくのはいいんですが,全く関係のないランダムな特徴量でも1に近づくのは問題です.(学習データでの)\(R^2\)を1に近づけるためには適当な特徴量を追加するればいいということになりますからね!
これを調整したのがadjusted R-Squaredと呼ばれる指標で,日本語では自由度調整済み決定係数と言います.
$$R^2=1-\frac{\frac{RSS}{m-n-1}}{\frac{TSS}{m-1}}$$
TSSに関しては特徴量の数によって変更はないので,\(m-1\)で割り,RSSは特徴量の影響を受けるので\(m-n-1\)で割っています.(\(m\)はデータ数,\(n\)は特徴量数です)
特徴量の数\(n\)が増えるとその分RSSが小さくなるように調整しているのがわかると思います.

その通り,評価をするのはあくまでもテストデータになるので,本来「特徴量を増やすと\(R^2\)が1に近づく」という問題を気にする必要はないのですが,特徴量を複数使った線形回帰(重回帰と言います)の文脈ではadjusted R-Squaredを用いることが多いので紹介しておきます.評価に使う際は\(R^2\)を使って構いません.

\(R^2\)は,\(\mathbf{X}\)がどれくらい\(\mathbf{y}\)を説明できているかの指標でもあるので,説明変数の寄与率を確認するという文脈では,学習データに対して\(R^2\)を見ることはあるでしょう.また,今後の記事で説明する「特徴量選択」の文脈でも,さまざまな特徴量の組み合わせでモデルを構築し,それぞれのモデルで学習データに対しての\(R^2\)をみて必要な特徴量を決めることもできます.(第6回で解説したp値も,テストデータ関係なく,学習データのみで判断できるんでした).この場合,テストデータを用意しなくとも学習データに対しての\(R^2\)をみるだけでいいと言えます.
Pythonでadjusted R-Squaredを計算する
scikit-learnでは,簡単にadjusted R-Squaredを計算する関数は用意されていません.
なので sklearn.metrics.r2_score から計算しましょう.
adjusted \(R^2\)は\(R^2\)を使って以下のように表すことができるので,
$$adjusted R^2=1-\frac{(1-R^2)(m-1)}{m-n-1}$$
これをPythonで書いてあげればOKです
|
1 2 3 |
r2 = r2_score(y_test, y_pred) adj_r2 = 1-(1-r2)*(len(X_test)-1)/(len(X_test)-len(X_test[0])-1) adj_r2 |
|
1 |
0.48813923052363783 |
また,学習データに対してadjusted \(R^2\)を見る場合には,第6回で紹介したstatsmodels.apiを使って学習済みのOLSに対して.summary()をcallすることで確認することができます.
|
1 2 3 4 5 |
import statsmodels.api as sma X2 = sma.add_constant(X) est = sma.OLS(y, X2) est_trained = est.fit() print(est_trained.summary()) |
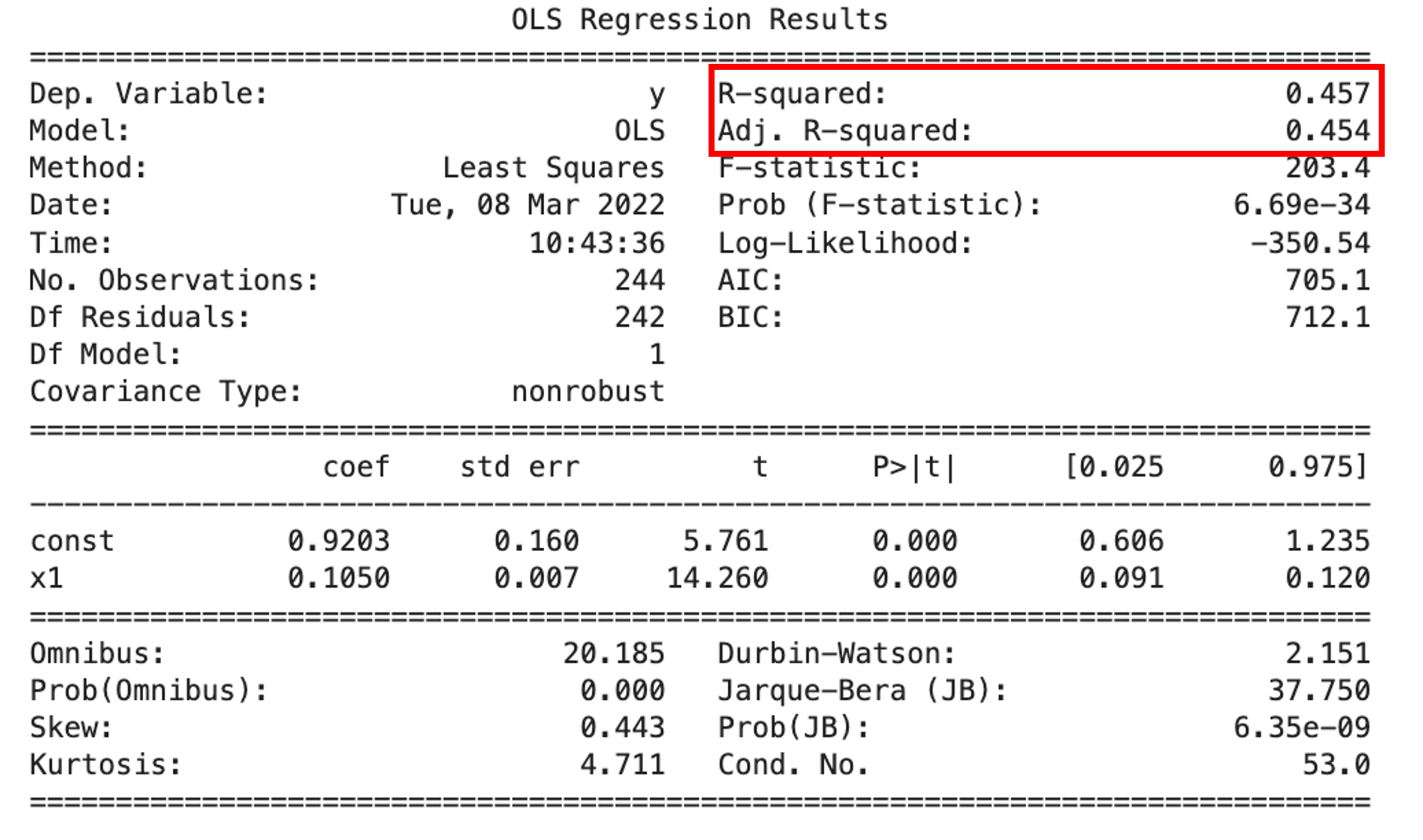 adjusted R-Squaredの方が,R-Squaredに比べて少しだけ小さくなっているのがわかると思います.特徴量を増やすとこの乖離は大きくなっておきます.
adjusted R-Squaredの方が,R-Squaredに比べて少しだけ小さくなっているのがわかると思います.特徴量を増やすとこの乖離は大きくなっておきます.
まとめ
今回の記事では,回帰モデルの評価指標を一挙解説しました.どれも実務でよく出てくる指標なので今回の記事でしっかり押さえておくといいです◎
- MSEは残差の二乗の平均で,損失関数として使われ,学習データにおけるMSEが最小になるようにパラメータを学習することから,評価指標として最もよく使われる指標の一つ
- RMSEは,MSEでは単位が二乗になってしまうため,それを緩和させるためMSEの平方根を取ったもので,目的変数と同じ尺度になるので感覚的に解釈しやすい
- MAEは残差の絶対値の平均で,実際の残差の大きさをそのまま平均しているので最も解釈しやすい
- R-Squaredは,データの当てはまりの良さを表す指標で,学習データに対して計算すると特徴量がどれくらい目的変数を説明しているかがわかり,テストデータに対して計算するとモデルの精度を表す.0から1の間になることから,扱いやすい数字であり,\(R^2=0.5\)で十分大きな値である
- adjusted R-Squaredは,学習データにおけるR-Squaredは,特徴量を増やすと例えその特徴量が目的変数と全く関係がなかったとしても1に近づく性質があるため,特徴量の数によって値を調整したもの.回帰の精度を見る文脈ではテストデータに対して\(R^2\)を計算すればいいのでadjusted R-Squaredを計算する必要はない
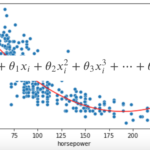
次回の記事では,線形回帰モデルを使った非線形表現ができる「多項式特徴量」について解説をしていきます.
線形モデルはわかりやすいですが,表現に限界があるのも事実.多項式特徴量を使うことでできる幅がぐんと広がります!
それでは!
追記)次回の記事書きました!