データサイエンス入門の機械学習編第16回です.(講座全体の説明と目次はこちら)
追記)機械学習超入門動画講座を公開しました!動画で効率よく学習をしたい人はこちら(現在割引クーポン配布中です)
前回までの記事では回帰問題における機械学習のアルゴリズムを解説してきました.
第1回で解説したように,機械学習のアルゴリズムには“分類”をするものもあります.
今回から,分類のアルゴリズムにフォーカスしてやっていきます.特に今回の記事では分類の最も基本的なアルゴリズムである「ロジスティック回帰」というものを紹介します.
おそらく分類は回帰以上に使われる機械学習のアルゴリズムなので,今回の記事でその基本をしっかり押さえておきましょう!
目次
分類(Classification)タスクについて
世の中には本当に多くの機械学習の分類タスクが実用化されています.
例えば顔認証やスパムメールのフィルタ,指紋認証や音声認識など,挙げればキリがありません.
分類タスクも基本は教師あり学習です.教師ラベルを元に学習をしていきます.
例えば,広さと家賃というデータから,その物件に駐車場が付いているかどうかを判定するアルゴリズムを考えてみましょう.
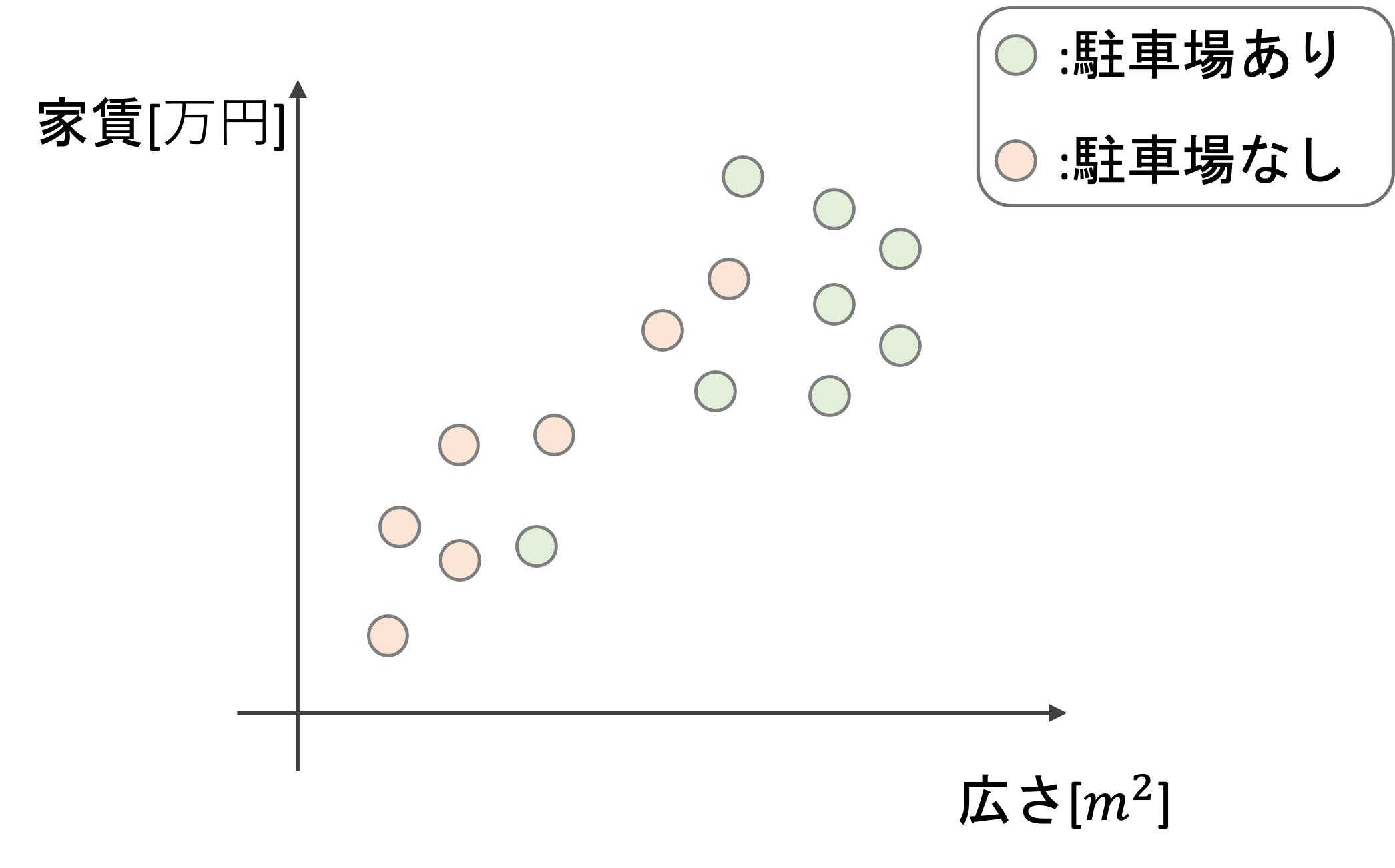
回帰の例では広さや駐車場の有無から家賃という連続した値を予測するんでしたが,分類の場合は連続値ではなく駐車場有/無などの2値やカテゴリー値(例えば色など)を予測します.(このようなタスクのことを英語ではclassificationといいます.この用語もよく使われるので覚えておきましょう.
この例では,広さと家賃が特徴量(説明変数)となり,駐車場の有無が目的変数となります.つまり,目的変数が量的変数ではなくて質的変数になるんですね.
機械学習を使うと例えば以下のような線で駐車場の有無の分類ができるようになります.
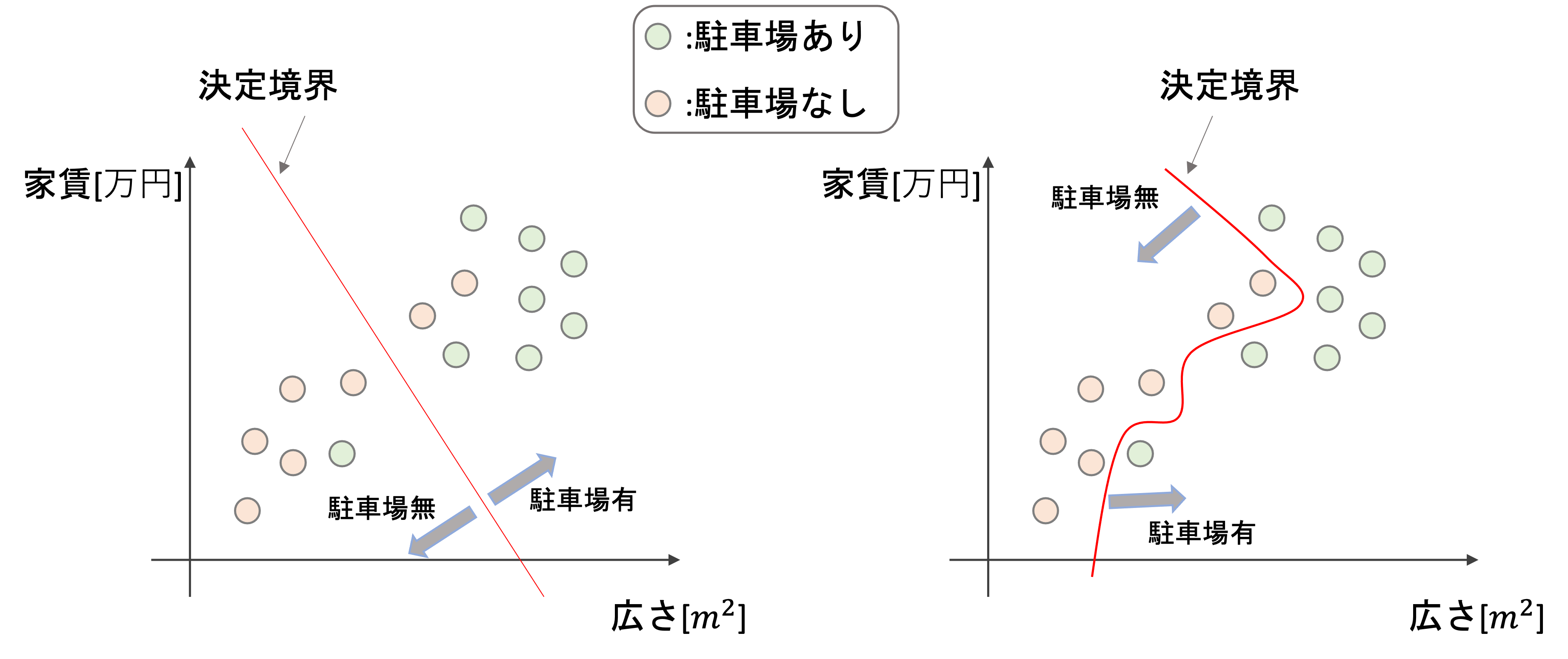
このように,分類の結果を決定づける境界線を決定境界(decision boundary)と言います.英語名もよく使われるので覚えておきましょう!
また,このように決定境界を引いてくれる機械学習モデルを分類器(classifier)というのでこれも日英ともに覚えておいてください!
機械学習の分類アルゴリズムの目的は,決定境界を引くことです.これはアルゴリズムによって線形(例:左図)だったり非線形(例:右図)だったりします.回帰タスク同様,完璧な決定境界を引くことは不可能で,ほぼ必ず誤って分類してしまうデータが存在することを念頭におきましょう.
分類をどうやってやるか(回帰をそのまま使えない

今まで学習してきた回帰のアルゴリズムは分類タスクには使えません.仮に駐車場の有/無を1/0という2値に変換して線形回帰をしたとしても,その回帰の結果は0〜1の範囲を超えます.
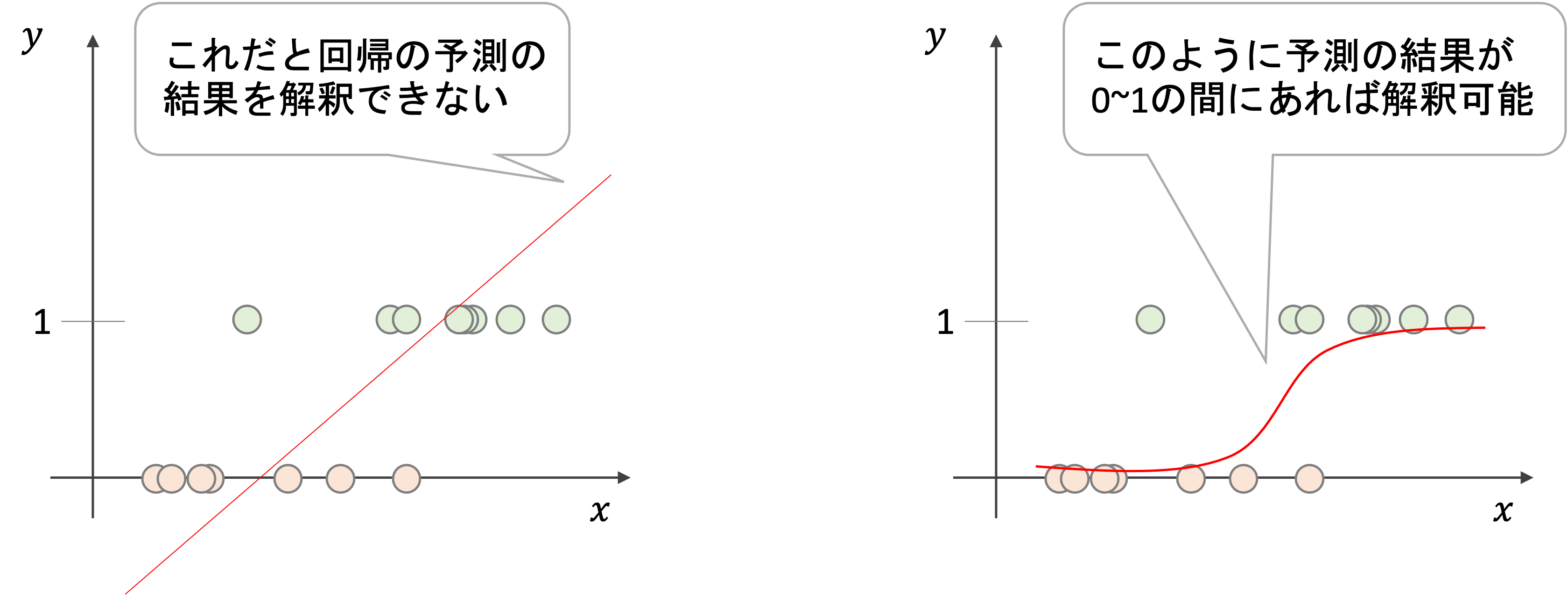
上図はイメージですが,ある特徴量\(x\)から0/1の値を取る目的変数\(y\)を予測する回帰直線を引いた場合(左図),ある値\(x_0\)の予測値\(\hat{f}(x_0)\)は0~1の範囲を超えた結果を返す場合があります.仮にその値が1.5だった場合,その値をどう解釈していいのかわかりません.(1を超えているから1としていいのか?)
分類タスクの場合,上の右図のように予測の結果が0~1の間であれば,その結果を“確率”として解釈することができます.
さらに,2値ではなく多クラス分類になると,それぞれの質的変数であるクラスを0, 1, 2,..のように数値化し量的変数として扱うことができません.(例えば赤,青,黄の3クラス分類をするとして,それぞれ0, 1, 2と数値を割り当てたとしても,青(1)が黄(2)の半分の値というわけではないので,数値として扱うことはできません)
他にも,一つ外れ値があっただけで回帰の結果が大きく変わってしまいますよね.(例えば上図で\(x\)が非常に高いところで一つだけ\(y=0\)がある場合を想定してみてください)

その通り!分類のアルゴリズムも回帰同様に色々とあるんですが,最も基本的な分類アルゴリズムであるロジスティック回帰(logistic regression)について解説します.
ロジスティック回帰(logistic regression)

名前がまたイカついですが,,,慣れましょう笑
ロジスティック回帰は”回帰”という名前がついてますが,分類器のアルゴリズムです.

なぜ”回帰”という名前になっているかについては,簡単にいうと実際に行っている作業が回帰だからなんですねぇ・・・この辺りはおいおいわかっていけばいいです.今はキニシナイキニシナイ・・・
シグモイド関数
回帰をそのまま分類に使う問題点の一つとして,回帰の結果が0~1の間に収まらないというのがありました.
そこで,シグモイド関数と呼ばれるものを使います.シグモイド関数はロジスティック関数とも呼ばれます.(だから”ロジスティック”回帰というんですね〜)
シグモイド関数は
$$z=\frac{1}{1+e^{-x}}$$
という式で表されます.
この式だけみても「??」だと思いますが,描画すると以下な感じです.

シグモイド関数は,どのような値\(x\)を入れても,その結果\(z\)は0から1の間に収まります.これを活用して先ほどの線形回帰の結果を0~1の間に収めることを考えます.
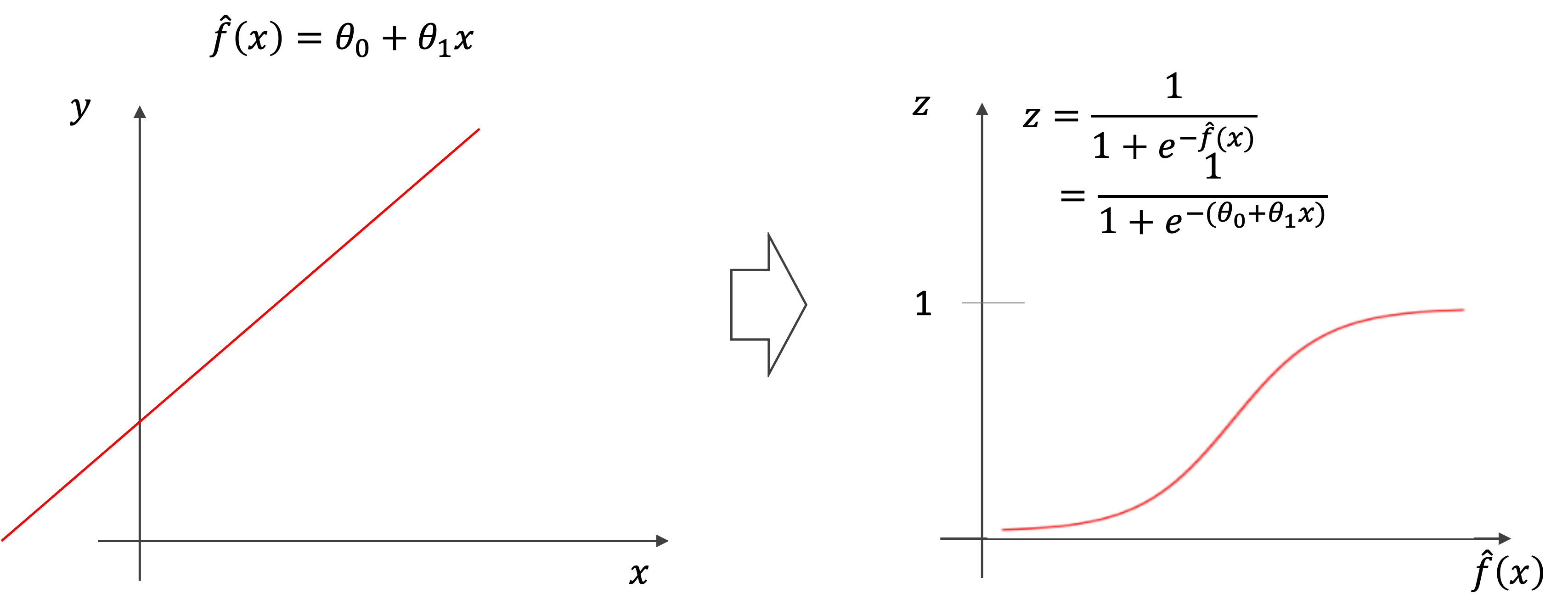
上述のシグモイド関数の\(x\)に線形回帰の結果である\(\hat{f}(x)\)を入れてあげれば,線形回帰の結果をうまく0~1に収めることができます.(上図の右の関数の線は途中で途切れていますが,0と1を漸近線としてずっと続くものだと思ってください.)
つまり,これこそがロジスティック回帰の数式のモデルです.
$$p(x)=\frac{1}{1+e^{-(\theta_0+\theta_1x)}}$$
ロジスティック回帰の結果は0~1の値になりますが,これはそのまま(ラベルが1である)確率として扱うことができるので,\(x\)を入力とした時の確率\(p(x)\)をロジスティック回帰の出力結果とすることができます.また,今回の例はわかりやすく特徴量が1つの場合の式になっていますが,特徴量が複数あっても同じです.
損失関数
ロジスティック回帰では,先ほどの式\(\frac{1}{1+e^{-(\theta_0+\theta_1x)}}\)におけるパラメータ\(\theta\)を求めることになります.
これは,他の機械学習のアルゴリズム同様,損失関数を定義して損失が最小になるようなパラメータを求めていきます.
では,どのような損失関数を使うのがいいでしょう?線形回帰の時は最小二乗法で,MSEやRSSを損失関数としていました.
線形回帰のように最小二乗法を使うと,\(\frac{1}{1+e^{-(\theta_0+\theta_1x)}}\)という非線形な複雑な式に対してさらに二乗をかますことになり,損失関数が複雑になってしまい,最適解を見つけるのが難しくなってしまいます.
そのため,ロジステイック回帰用の損失を別に定義する必要があるのです.
では,どんな損失を使うか?答えは,log lossと呼ばれる以下のようなLogarithmを使った損失を使います.他にも交差エントロピー(cross entropy)とも呼ばれます.データ\(i\)における損失を\(Cost(p(x_i), y_i)\)とすると
\begin{equation}
Cost(p(x_i), y_i)=\left\{
\begin{aligned}
-log(p(x_i)) & \qquad\text{if}\:y_i=1\\
-log(1-p(x_i)) & \qquad\text{if}\:y_i=0\\
\end{aligned}
\right.
\end{equation}

一見難しそうに見えますが,実はそんなに難しいものではないので一つ一つみていきましょう!
真の値が1の時(y=1)
上の式では,\(y_i=1\)の時損失は\(-log(p(x_i))\)とありますが,これは以下のようなグラフになります.
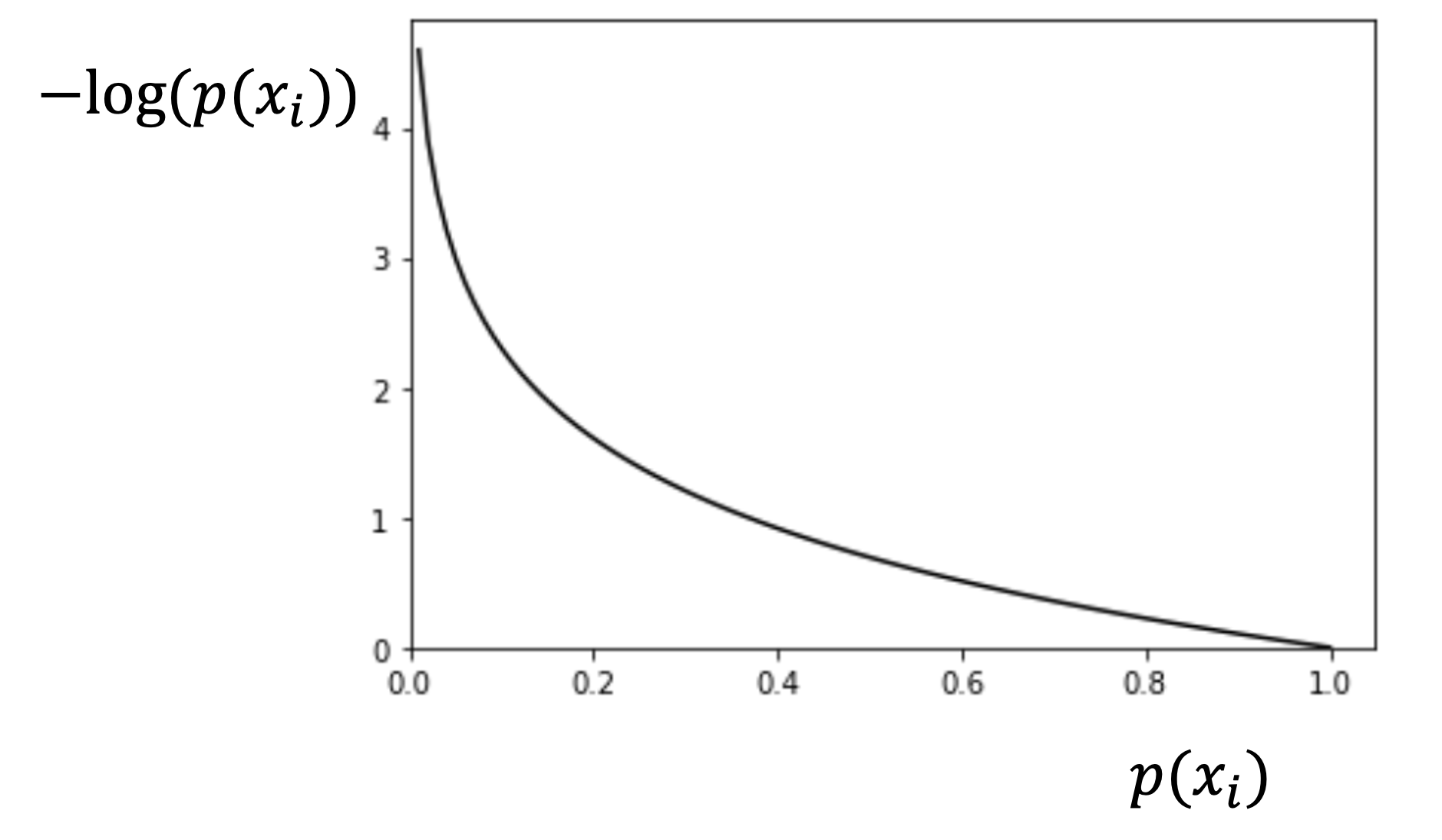
\(p(x_i)\)は0〜1の間の値しか取らないことに注意しましょう.
\(p(x_i)=1\)の時は,\(y_i=1\)に対しての分類結果が1になるので,損失は0になります.\(p(x_i)\)が下がっていくにつれて損失は高くなっていき\(p(x_i)=0\)では\(-log(p(x_i))=\infty\)となり,損失は無限です.これは当然,\(y_i=1\)のデータに対して分類結果を確率100%で0にしてしまうので,当然損失が高くなるということですね!
例えば駐車場が付いていない物件に対して「駐車場がついている確率100%!!」と結論づけてしまう場合は損失が無限大ってことです.
それでは,\(y_i=0\)の時もみてみましょう
真の値が0の時(y=0)
\(-log(1-p(x_i))\)は以下のようになります.上記の\(-log(p(x_i))\)の左右逆転版ですね.
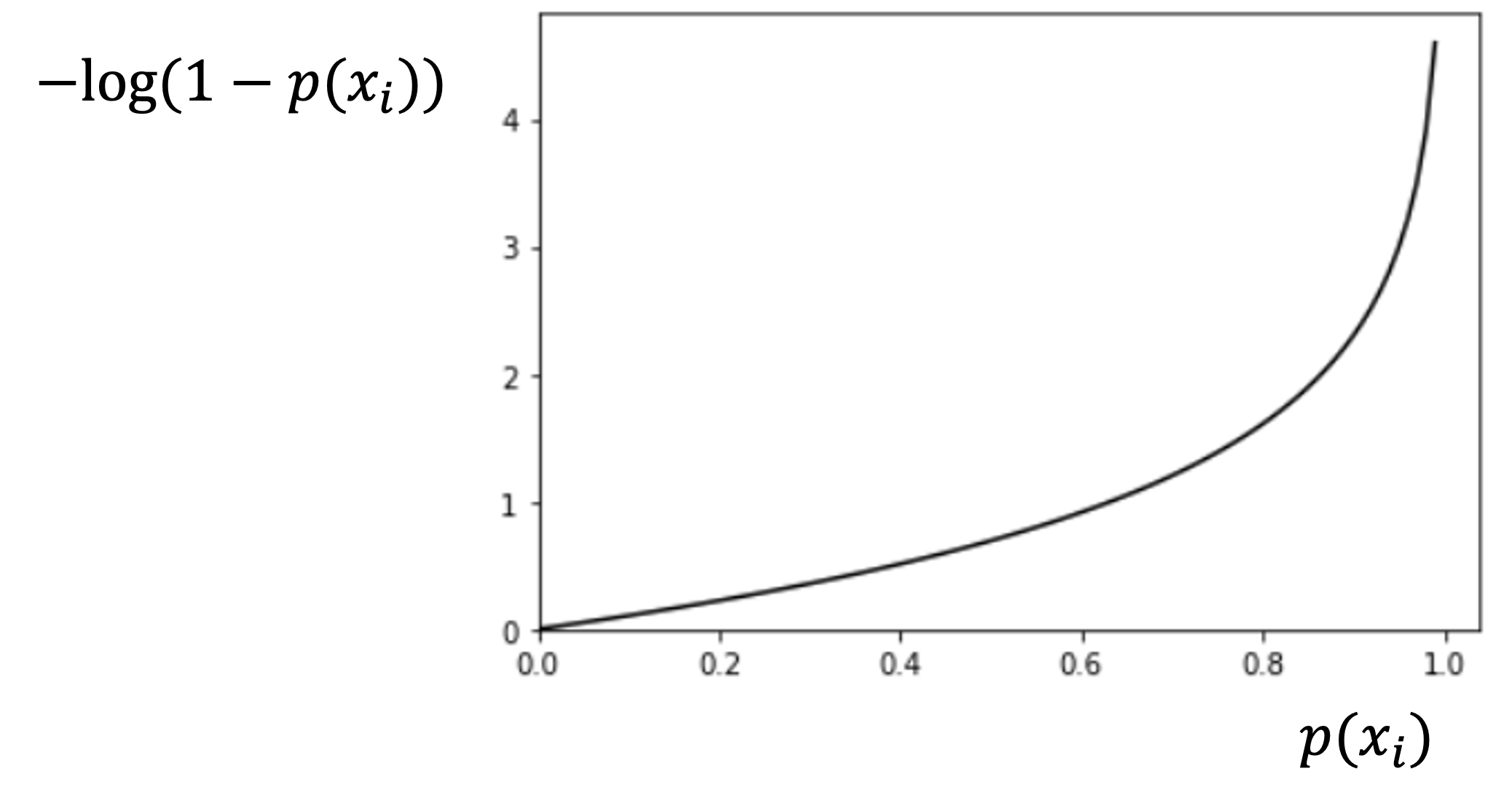
これも\(y_i=1\)の時と同様に見ることができます.\(y_i=0\)のデータに対して\(p(x_i)=0\)とした時の損失は0で,\(p(x_i)\)が大きくなるにつれ,真の値1から遠ざかり,損失も上がっていき,\(p(x_i)=1\)の時に損失無限大になります.
式だけみるとわかりにくいかもしれませんが,一つ一つ丁寧に読み取っていくと直感的に理解できるのではないでしょうか?
今回わかりやすく二つの式を\(y_i=0\)の時と\(y_i=1\)の時で分けて記載しましたが,これは一つの式で表すこともできます.できればこちらの式で覚えておきましょう!
$$Cost(p(x_i), y_i)=-(y_ilog(p(x_i))+(1-y_i)log(1-p(x_i)))$$
このようにすれば\(y_i=0\)の時に\(y_ilog(p(x_i))\)が0になり,\(log(1-p(x_i))\)だけが残り,また\(y_i=1\)の時に\((1-y_i)log(1-p(x_i))\)が0になり\(y_ilog(p(x_i))\)だけが残り,先ほどの二つの式を表すことになります.(\(y_i\)は0か1しかとり得ないことに注意してください)
そしてこの損失を全てのデータで平均をとったものが損失関数です.(これは合計でも構いません.今回は平均の式を損失関数として記載しておきます.)
$$L(\theta)=\frac{1}{m}\sum^{m}_{i=1}Cost(p(x_i), y_i)=-\frac{1}{m}\sum^{m}_{i=1}y_ilog(p(x_i))+(1-y_i)log(1-p(x_i))$$
ただし,\(\theta=\theta_0, \theta_1\cdots\theta_n\)です.一見ややこしく見える数式ですが,上述のように一つ一つ丁寧にみていけば理解できるのではないでしょうか?
最適化アルゴリズムで最適解を求める
損失関数さえ定義してしまえば,あとは最適化のアルゴリズムで最適解を求めていけばOKです.
線形回帰の例では最急降下法(gradient descent)というものを紹介しました.最適化アルゴリズムには他にも色々と種類がありますが,本講座では対象外とします.(今後機会があったら記事にしたいです.色々な最適化アルゴリズムを学ぶだけで一つの講座が作れるくらい奥が深いです)
第3回同様,最急降下法では以下のように\(\theta_0\), \(\theta_1\)を同時に更新していくんでしたね.
$$\theta_0 := \theta_0 – \alpha\frac{\partial}{\partial\theta_0}L(\theta_0, \theta_1)$$
$$\theta_1 := \theta_1 – \alpha\frac{\partial}{\partial\theta_1}L(\theta_0, \theta_1)$$
ただし,:=は代入演算子です. (最急降下法については第3回を参考にしてください) また,\(\alpha\)は学習率と呼ばれるハイパーパラメータでしたね.
さて,ここで気になるのは\(\frac{\partial}{\partial\theta}L(\theta)\)ですね.これはそこまで難しい計算ではないのですが,長くなるし導出はそこまで重要ではないので本記事では割愛します...(また機会があったら補足記事書きます.興味がある人はやってみてください.
\(\frac{\partial}{\partial\theta}L(\theta)\)を計算すると,最終的には以下の式になります.
$$\frac{\partial}{\partial\theta_0}L(\theta_0, \theta_1)=\frac{1}{m}\sum^{m}_{i=1}(p(x_i)-y_i)$$
$$\frac{\partial}{\partial\theta_1}L(\theta_0, \theta_1)=\frac{1}{m}\sum^{m}_{i=1}(p(x_i)-y_i)x_i$$

そうなんです.\(p(x_i)=\hat{y}_i\)と考えたら全く同じ形をしています.
つまり,最小二乗法の線形回帰と同じ式を使ってパラメータの更新を行うことができるということです.
あとは第3回同様に,パラメータ\(\theta_0, \theta_1\)を最急降下法によって求めていけばいいわけです.
今後の記事ではscikit-learnを使って実際にロジスティック回帰のモデルを構築してサンプルデータで分類してみたいと思います.
今回の記事でいまいち理解できなかったとしても大丈夫です.今後の記事で実際に分類器を作って,それがどのように使えるのかを見ればより理解が深まると思うので,是非このまま次の記事に進んでみてください!
多クラス分類について

そうなんです.ロジスティック回帰は基本的には2クラス問題専用なんです!
が,多クラス分類に応用することができます.
これについてはまた長くなるので次の記事にて解説します〜!!現実の問題では2クラスより多クラス分類をする方が多いですからね!次の記事でしっかり学習を進めていきましょう〜
まとめ
今回の記事では分類タスクとロジスティック回帰について解説しました.
- 回帰モデルをそのまま分類タスクには使えない
- 理由は1. 結果が0~1の間に収まらないから 2. 質的変数を0, 1, 2.. と数値化したところで量的変数として扱えないから 3.外れ値の影響を大きく受けてしまうから
- 回帰の結果を0~1の間に収めるためにシグモイド関数(ロジスティック関数)を使うのが,ロジスティック回帰
- 損失関数には交差エントロピー(log loss)を使う
- 最急降下法によるパラメータ更新の式は線形回帰のそれと同じ式になる
分類タスクは多分回帰タスクよりも使われることが多いです.その分重要度も高いので,今後の記事でしっかり学習していきましょう!
また,ロジスティック回帰は分類タスクの最も基本的なアルゴリズムになるので必ず押さえておきましょう
次回の記事ではロジスティック回帰の多クラス応用について解説をします.
それでは!
追記)次の記事書きました!