多クラス分類におけるROCとAUC【機械学習入門23】

こんにちは，米国データサイエンティストのかめ(@usdatascientist)です．

データサイエンス入門の機械学習編第23回です.(講座全体の説明と目次はこちら)

追記)機械学習超入門動画講座を公開しました！動画で効率よく学習をしたい人はこちら(現在割引クーポン配布中です)

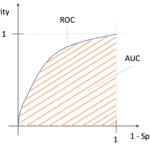
前回の記事でROCとAUCについて解説をしましたが，前回の記事は２クラス分類に特化した解説になっていました．

今回の記事では前回の記事の内容をベースに，多クラス分類におけるROCとAUCをどうやって計算するのかを解説していきます．

実際の業務では多クラス分類を扱うことは非常に多いので，この機会に学習しておきましょう！

基本はOvR

多クラス分類の精度を考える際は，やはりOne vs Restが基本になります．(他のやり方もありますが，OvRが最も一般的です．OvRについては第17回でも出てきましたね．)

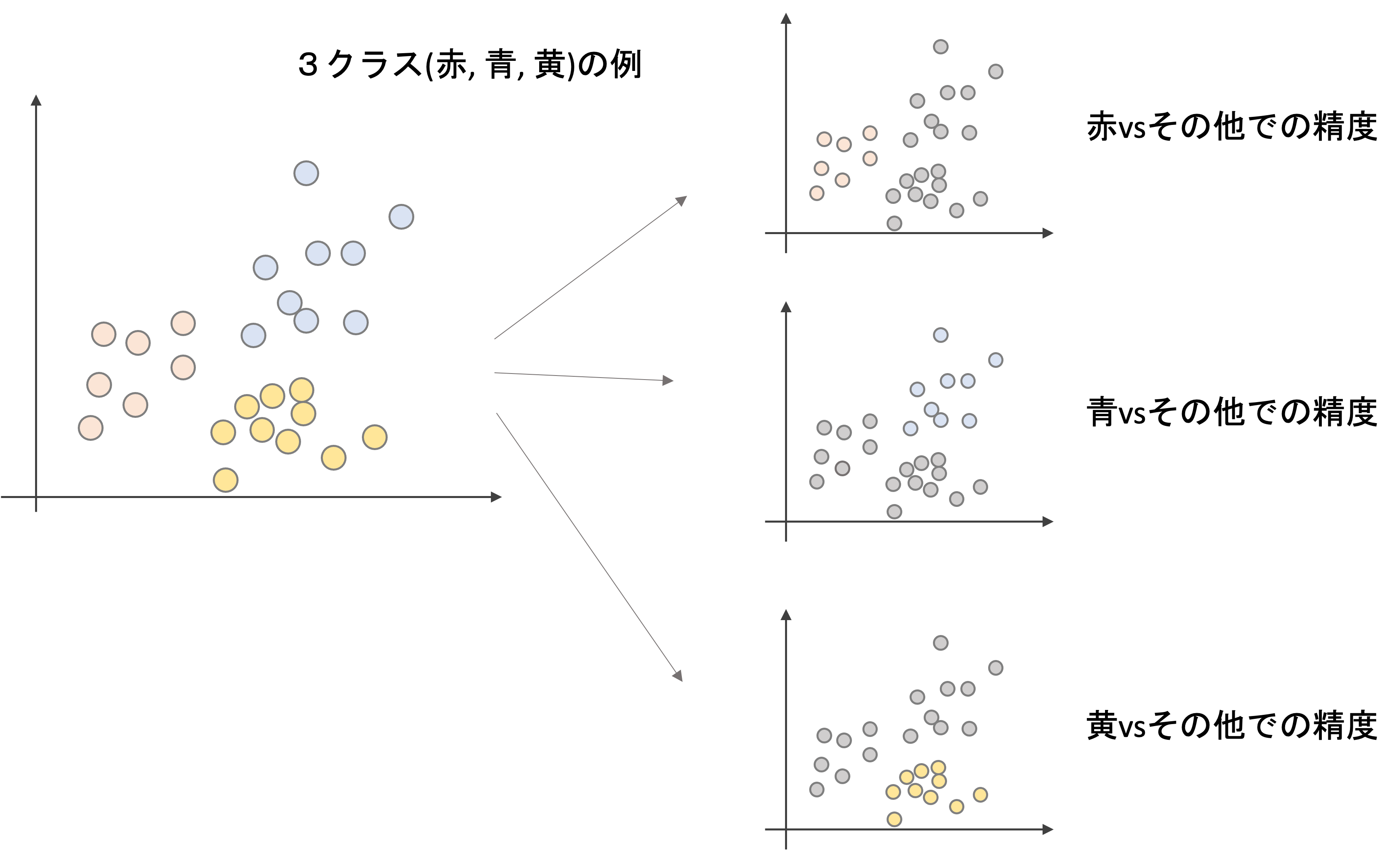
上図は３クラス(赤，青，黄)の例です．この場合，それぞれのクラスvsその他のクラスの3パターンの精度を測ります．

つまり，多クラス分類のROCでは，クラスの数分ROCを描くことができるわけです．

それではまずはPythonで３クラス分類におけるROCを実際に描いてみましょう！

Pythonでそれぞれのクラス(OvR)のROCを描いてみる

今までの記事通り，今回もirisデータセットを使います．

ロジスティック回帰モデルで分類器を作って，ROCを描いてみましょう！学習のコードは第18回を参考にしてください．

import seaborn as sns
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split

# データロード
df = sns.load_dataset('iris')
# 学習データとテストデータ作成
X = df.loc[:, df.columns!='species']
y = df['species']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
# モデル構築
model = LogisticRegression()
model.fit(X_train, y_train)
# 予測(確率)
y_pred_proba = model.predict_proba(X_test)

import seaborn as sns

from sklearn.linear_model import LogisticRegression

from sklearn.model_selection import train_test_split

# データロード

df = sns.load_dataset('iris')

# 学習データとテストデータ作成

X = df.loc[:, df.columns!='species']

y = df['species']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

# モデル構築

model = LogisticRegression()

model.fit(X_train, y_train)

# 予測(確率)

y_pred_proba = model.predict_proba(X_test)

それでは，それぞれのクラス毎のROCを描いていみます．基本は前回の記事と同じです． roc_curve() 関数を使います．

クラスの数だけROCを描くための fpr , tpr を求めるので，for文で回します．OvRにするため，それぞれの roc_curve() の引数に渡す y_true と y_score は，それぞれのクラスに対してのラベルとスコアを渡すことになります．

ここで，今の y_test はクラス名が値になったSeriesの形になっているので,これをone-hot vectorの形にエンコードします．

第13回ではDataFrameに対して簡単にダミー変数を作れる .get_dummies() を紹介しましたが，今回はダミー変数にしたいのではなく，単にone-hot エンコーディングがしたいだけです．こういう場合は， sklearn.preprocessing.label_binarize を使います．

label_binarize 関数は，第一引数に y (ラベルのリスト)を渡し，第二引数に classes (クラスのリスト)を渡せばOKです．

例えば，今の y_test にはこんなデータが入っているので，

y_test[:5]

1	y_test[:5]

114     virginica
62     versicolor
33         setosa
107     virginica
7          setosa
Name: species, dtype: object

114 virginica

62 versicolor

33 setosa

107 virginica

7 setosa

Name: species, dtype: object

mode.classes_ を使って

model.classes_

1	model.classes_

array(['setosa', 'versicolor', 'virginica'], dtype=object)

1	array(['setosa', 'versicolor', 'virginica'], dtype=object)

以下のようにone-hotエンコーディングを施すことができます．

from sklearn.preprocessing import label_binarize
y_test_one_hot = label_binarize(y_test, classes=model.classes_)
y_test_one_hot[:5]

from sklearn.preprocessing import label_binarize

y_test_one_hot = label_binarize(y_test, classes=model.classes_)

y_test_one_hot[:5]

array([[0, 0, 1],
       [0, 1, 0],
       [1, 0, 0],
       [0, 0, 1],
       [1, 0, 0]])

array([[0, 0, 1],

[0, 1, 0],

[1, 0, 0],

[0, 0, 1],

[1, 0, 0]])

これを使って，それぞれのクラスの fpr , tpr を計算していきましょう！

from sklearn.metrics import roc_curve, auc
n_classes = 3
fpr = {}
tpr = {}
roc_auc = {}
for i in range(n_classes):
    fpr[i], tpr[i], _ = roc_curve(y_test_one_hot[:, i], y_pred_proba[:, i])
    roc_auc[i] = auc(fpr[i], tpr[i])

from sklearn.metrics import roc_curve, auc

n_classes = 3

fpr = {}

tpr = {}

roc_auc = {}

for i in range(n_classes):

fpr[i], tpr[i], _ = roc_curve(y_test_one_hot[:, i], y_pred_proba[:, i])

roc_auc[i] = auc(fpr[i], tpr[i])

roc_curve で計算する際に [:, i] でスライシングすることで特定のクラスのラベルとスコア(確率)のみを抽出していることに注意しましょう！

それではこの fpr , tpr からROCを3つplotすればOKです．

import matplotlib.pyplot as plt
%matplotlib inline
for i in range(n_classes):
    plt.plot(fpr[i], tpr[i], label=f'class: {i}')
plt.legend()

import matplotlib.pyplot as plt

%matplotlib inline

for i in range(n_classes):

plt.plot(fpr[i], tpr[i], label=f'class: {i}')

plt.legend()

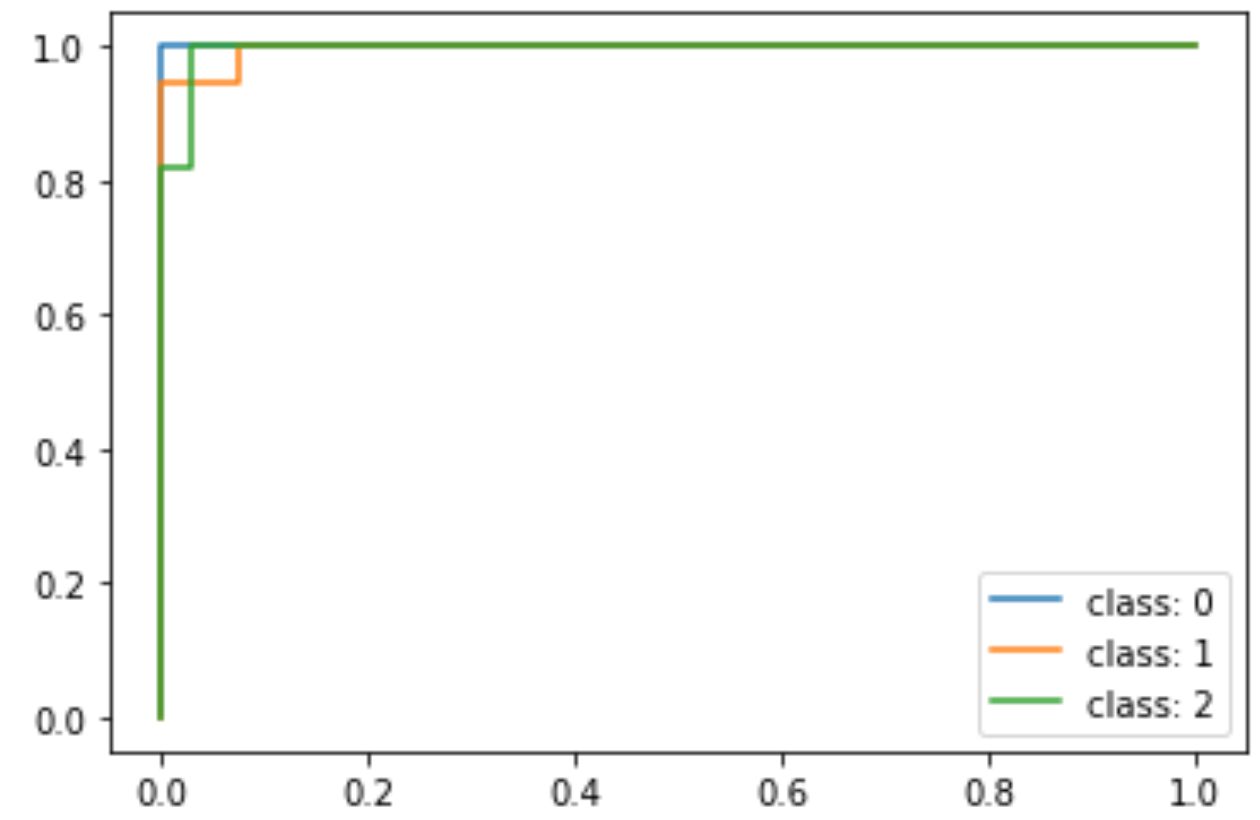
irisデータセットは分類が非常に簡単なデータセットなので，かなり精度が良いROCに仕上がってるのがわかります．class 0, 1, 2はそれぞれ’setosa’, ‘versicolor’, ‘virginica’です．’setosa’に関してはAUCが1の完璧なROCを描いています．

ひとまずこれが，OvRでの多クラスのROCです！

macro平均とmicro平均

でも，実際に欲しいのは最終的な評価指標だよね？それはどうやって求めるの？

そうですよね，ROCがクラスの数だけあったら評価しにくいですよね．3つならまだしも，これが10クラスとかだと大変です．最終的に「これ！」といえる評価指標が必要です．

そこで出てくるのが，第20回で紹介したmacro平均とmicro平均です．

macro平均

クラスレベルでの平均です．それぞれのクラス毎の値を足して，クラス数で割ります．大きなレベルでの平均になるので”macro”なんですね

micro平均

データレベルでの平均です．各データの値を足して，データ数で割るイメージです．小さなレベルでの平均になるので”micro”なんですね.ROCの場合は，クラスは無視してデータ全体でROCを描いていきます(後述)

使い分け

micro平均を取ると，クラス毎にデータ数に偏りがある場合データ数が多いクラスの結果が大きく反映されてしまいます．データ数が少ないクラスの値も重視したい場合は，macro平均をとることで，それぞれのクラスの値が平等に平均値に反映することができます．(この辺りも記事の最後に後述します)

さて，これらを先ほどのROCにどのように適用できるか考えてみましょう！

多クラスROCのmacro平均

macro平均は，単純に各クラスの平均をとっていけばOKです．

例えば以下のように4クラスのROCがある場合，その平均をとった真ん中のROCカーブになります．(図はイメージです．実際の値ではありません．)

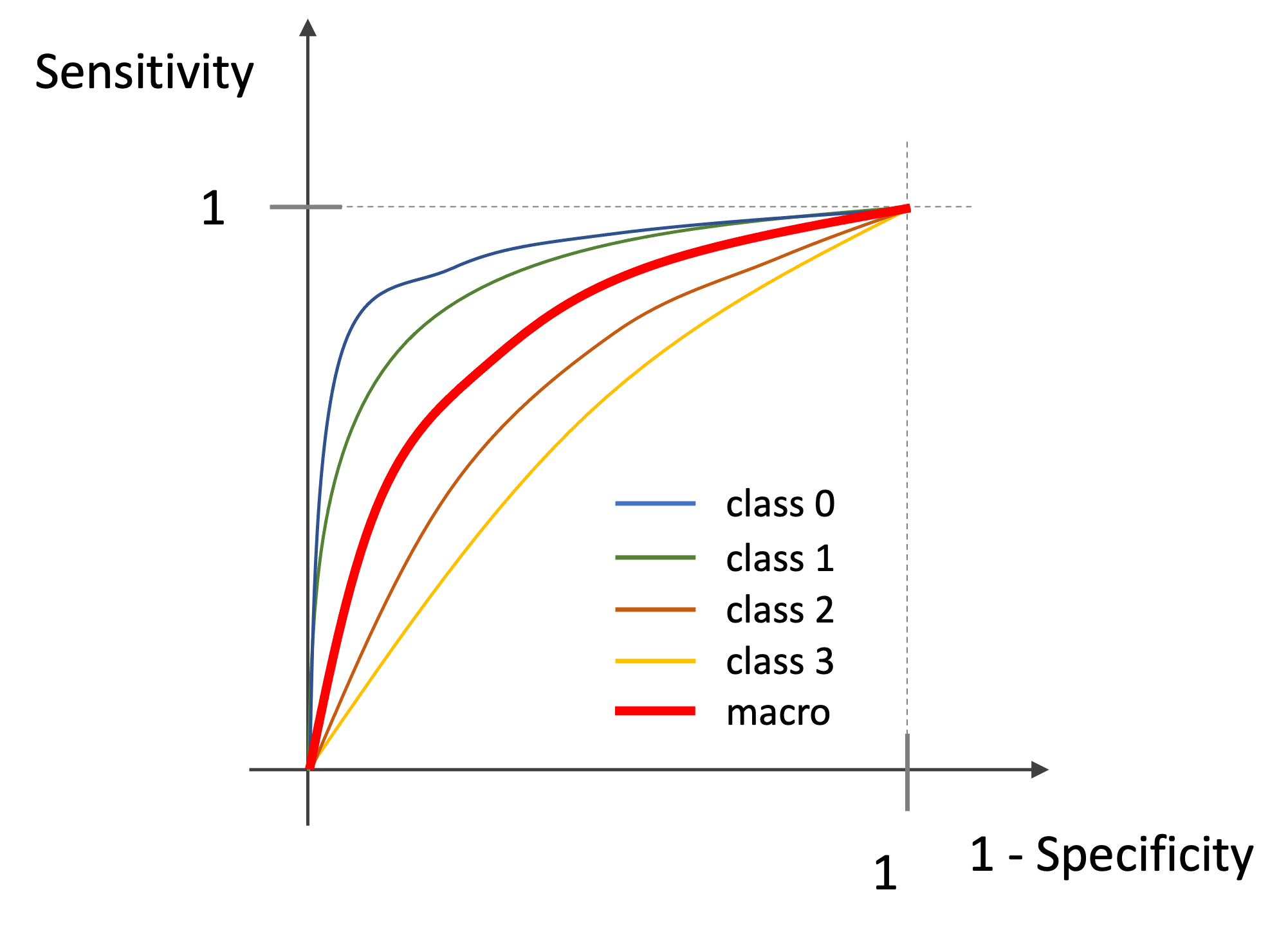
ようは，単純にそれぞれの1-Specificity(FPR)におけるSensitivity(TPR)の平均をplotしていけば，macro平均のplotが出来上がります．

考え方はシンプルですが，これを実装するのは少し工夫が必要です．

Step by stepに易しく解説するので是非ついてきてください！(以下，記述をシンプルにするために1-Specificity=FPR=xの値、Sensitivity=TPR=yの値とします．)

まず，先ほどの３クラスそれぞれのROCを見てみましょう．それぞれの平均を取る際に，それぞれのxの値に対するyの値の平均を取るんですが，これは値に変化があるxに対してのyの平均のみを取ればいいですよね．そうすることで，いちいち全てのxで平均を取る必要がありません．

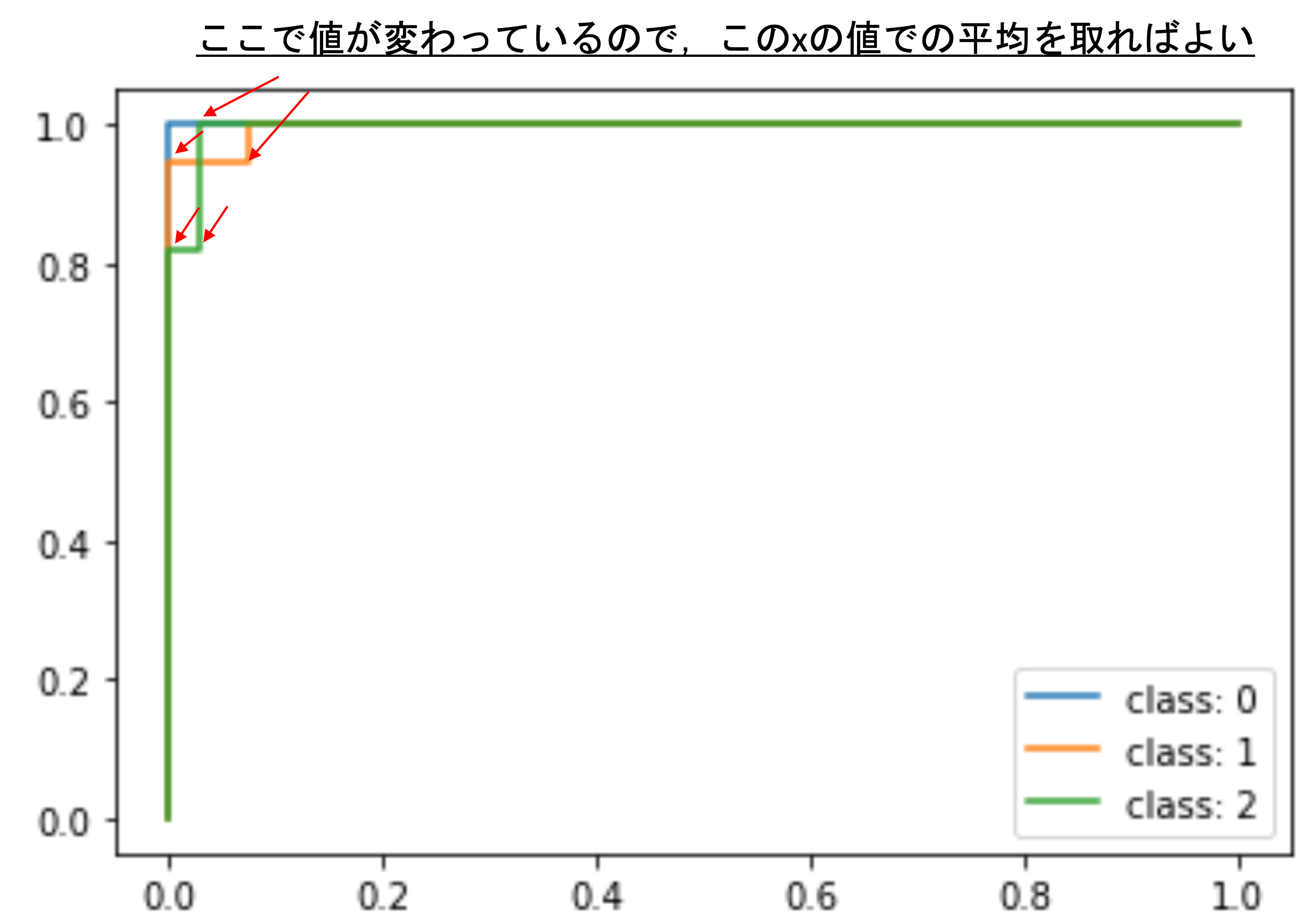
つまりはx軸の値が変更している点だけを得られればいいので，以下のようにして該当するfpr(xの値)をリスト化します．

import numpy as np
all_fpr = np.unique(np.concatenate([fpr[i] for i in range(n_classes)]))

1 2	import numpy as np all_fpr = np.unique(np.concatenate([fpr[i] for i in range(n_classes)]))

なにやら複雑そうな一行ですが，やってることはシンプルで，今回得られた3つのfprの値を重複しない形で一つのリストにしているだけです．つまり，この値に対してのみyの値(tpr)の平均をとっていけばいいことになります．

それでは，次にそのxの値に対してのそれぞれのクラスのyの値を平均していきます．

この時，yの値は tpr に入っていますが，全てのxに対してのyが全てのクラスの tpr に入っているわけではありません．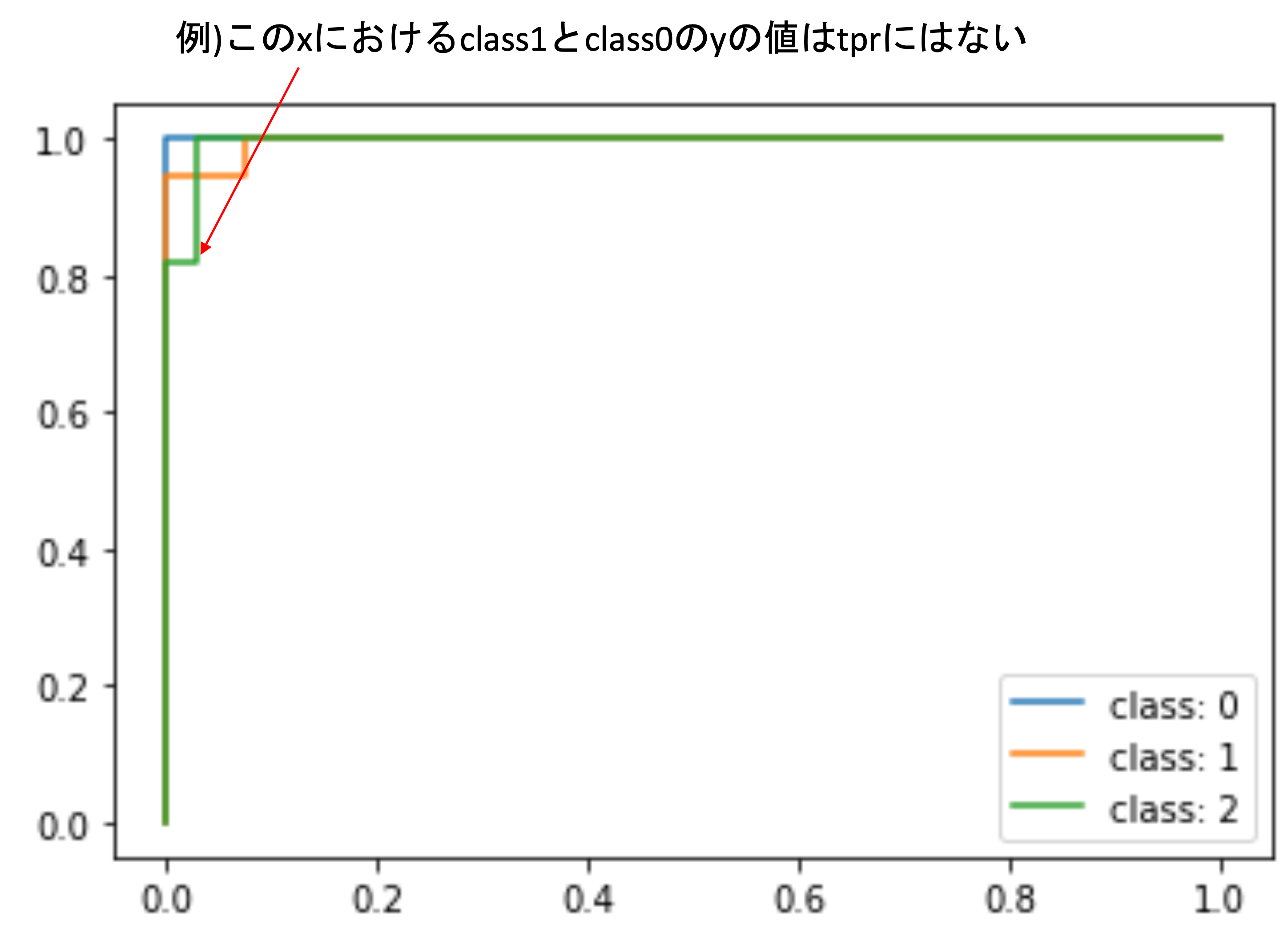

上の例では，class 2のyの変換点におけるxなので，他のクラスにはこのxに対してのyの値が tpr には格納されていないんですね

ではどうするのかというと，補完(interpolation)をします．

例えば下の例をみてください．

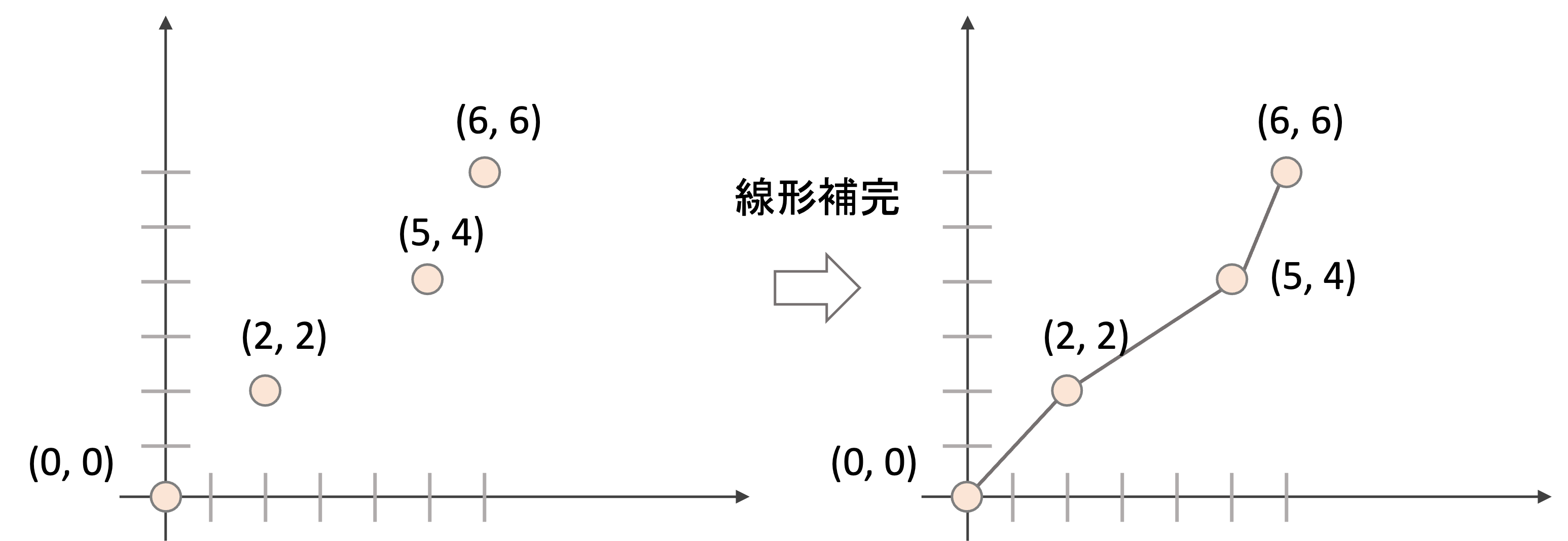
このように二次元座標上に4点の値がある場合，途中のxの値に対するyの値を出すには，点と点を補完(interpolate)する必要があります．

補完の方法は色々ありますが，単純に直線で補完する線形補完(linear interpolation)というのが最もシンプルなやり方です．(補完は機械学習でも結構重要なアルゴリズムなので，機会があったらやりたいですね)

例えば上の例では，x=1におけるyの値は，線形補完後はy=1　と．値を出すことができます．今回のROCに対してもこの補完を行うことでそれぞれのyの値を計算していきます．

これは np.interp という関数を使って行うことができます．引数は以下の値をとります．

x : x軸の値のリスト (補完後に評価したい座標のx軸の値)
xp : 補完するデータのx軸の値のリスト
yp : 補完するデータのy軸の値のリスト

つまり，上の例を np.interp で補完をすると，以下のように書くことができます．(わかりやすい変数名にするため，本来の引数名と異なる変数名にしています．)

all_x = np.arange(7)
data_x = [0, 2, 5, 6]
data_y = [0, 2, 4, 6]
np.interp(all_x, data_x, data_y)

all_x = np.arange(7)

data_x = [0, 2, 5, 6]

data_y = [0, 2, 4, 6]

np.interp(all_x, data_x, data_y)

array([0.        , 1.        , 2.        , 2.66666667, 3.33333333,
       4.        , 6.        ])

1 2	array([0. , 1. , 2. , 2.66666667, 3.33333333, 4. , 6. ])

このように， all_x の値に対しての補完後のyの値が返ってきます．

上の図の補完後の座標と見比べたら，これが線形補完されている座標の値だということがわかると思います．

ではこれを使って先ほどのx軸の値( all_fpr )に対するそれぞれのクラスのROCの補完した値の平均を計算します．

mean_tpr = np.zeros_like(all_fpr)
for i in range(n_classes):
    mean_tpr += np.interp(all_fpr, fpr[i], tpr[i])
mean_tpr = mean_tpr / len(model.classes_)
mean_tpr

mean_tpr = np.zeros_like(all_fpr)

for i in range(n_classes):

mean_tpr += np.interp(all_fpr, fpr[i], tpr[i])

mean_tpr = mean_tpr / len(model.classes_)

mean_tpr

array([0.92087542, 0.98148148, 1.        , 1.        ])

1	array([0.92087542, 0.98148148, 1. , 1. ])

まずは， np.zeros_like() で要素の値が0の all_fpr と同じ長さのNumpy Arrayを作ります(place holder的な役割ですね).

このArrayに補完したyの値を入れていき，全てのクラスのROCに対する補完したyの値を足し合わせていって，最後にクラスの数で割れば平均を計算できます．

これを変数に格納してplotしてあげればmacro平均でのROCが描けます．また，AUCに関しては，macro平均したfprとtprから auc 関数を使って普通に求めればOKです．

fpr["macro"] = all_fpr
tpr["macro"] = mean_tpr
roc_auc["macro"] = auc(fpr["macro"], tpr["macro"])

for i in range(n_classes):
    plt.plot(fpr[i], tpr[i], label=f'class: {i}')
plt.plot(fpr['macro'], tpr['macro'], label='macro')
plt.legend()

fpr["macro"] = all_fpr

tpr["macro"] = mean_tpr

roc_auc["macro"] = auc(fpr["macro"], tpr["macro"])

for i in range(n_classes):

plt.plot(fpr[i], tpr[i], label=f'class: {i}')

plt.plot(fpr['macro'], tpr['macro'], label='macro')

plt.legend()

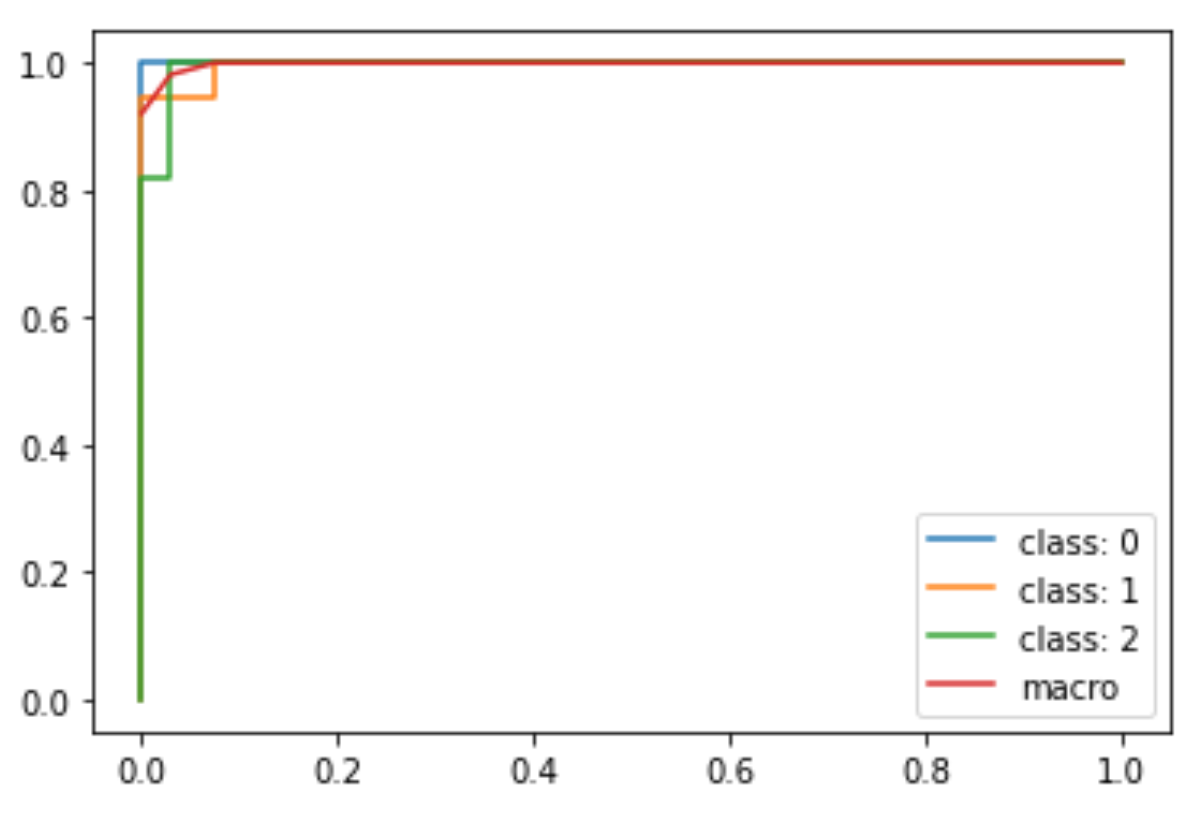
マクロ平均のAUC( roc_auc['macro'] )は，0.998と，非常に高い数字になっています．

少し長くなってしまいましたが，これがmacro平均です．考え方はシンプルなんですが，実装しようとすると少し工夫が必要なんですね〜

多クラスROCのmicro平均

micro平均は，クラス単位で平均を取るのではなく，データレベルでの平均です．

これはどういう風に計算できるかというと，macro平均ではそれぞれのクラスの情報をslicingして抽出して，それぞれのクラスのfpr, tprを求めていました. micro平均では，これをクラスの違いを無視して計算するので，全部一緒くたにして計算します．そうすることで，データレベルでのROCを描くことができます．

これをPythonのコードにすると，以下のようになります． .ravel() で，NumpyArrayを一次元にします．( .flatten() でもOKです．)

fpr['micro'], tpr['micro'], _ = roc_curve(y_test_one_hot.ravel(), y_pred_proba.ravel())
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])

1 2	fpr['micro'], tpr['micro'], _ = roc_curve(y_test_one_hot.ravel(), y_pred_proba.ravel()) roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])

これを同じようにplotすればOKです．

for i in range(n_classes):
    plt.plot(fpr[i], tpr[i], label=f'class: {i}')
plt.plot(fpr['macro'], tpr['macro'], label='macro')
plt.plot(fpr['micro'], tpr['micro'], label='micro')
plt.legend()

for i in range(n_classes):

plt.plot(fpr[i], tpr[i], label=f'class: {i}')

plt.plot(fpr['macro'], tpr['macro'], label='macro')

plt.plot(fpr['micro'], tpr['micro'], label='micro')

plt.legend()

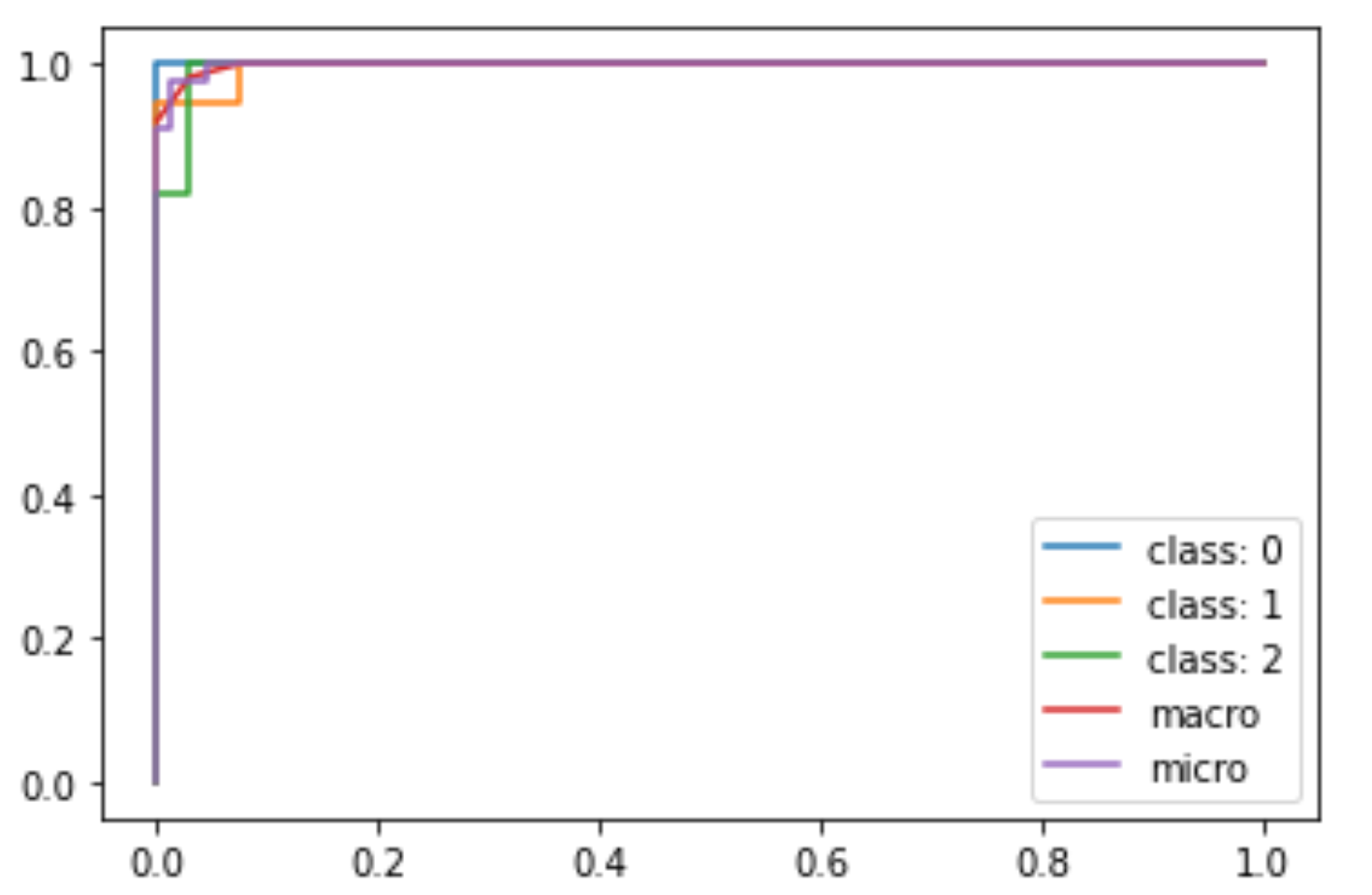
少し見にくいですが，micro平均のROCが描かれているのがわかると思います．

興味がある人は，もっとわかりやすいデータセットでやってみてください！

macro平均を使うかmicro平均を使うか

今回のデータセットではそれぞれのクラスのデータ数が同じなので，macroでもmicroでもいいと思います．データ数に偏りがある場合は

データ数が小さいクラスも他のクラスと同じくらい結果に反映させたければmacro平均を
データ数が多ければ多いだけ結果に反映させたければmicro平均を

使うのがいいと思います．ROCは非常によく使われる指標ですが，ひとたび”多クラス”になると「？？？」になる人も多く，macro平均とmicro平均の特徴を理解していない人が多いので，もし誰かに結果を報告する際はどちらも提示した上でそれぞれの特徴を明記するといいでしょう！

まとめ

今回は多クラス分類におけるROCとAUCの計算の仕方を紹介しました．(ROCが描けてしまえば，AUCはただ面積を求めるだけですね)

多クラス分類のROCを書くには，各クラスごとにOvR(One vs Rest)でSensitivity(TPR)と1-Specificity(FPR)を計算する
平均の取り方は主に2通りで
- macro平均: クラス毎にSensitivity(TPR)と1-Specificity(FPR)を計算し，クラス間で平均を取ってROCを描く
- micro平均: データ全体でSensitivity(TPR)と1-Specificity(FPR)を計算し，ROCを描く
小さいデータ数のクラスも均等に結果に反映させたければmacro平均を使い，データの偏りを気にせず，単に全体の評価を見る場合はmicro平均を使う
多クラス分類のROCを描く際は，扱いやすいようにラベルのデータをone-hot エンコーディングする
macro平均をPythonで描く際には，線形補完などを使いうまく各クラス間のSensitivity(TPR)の平均を計算する
micro平均をPythonで描く際は，全てのデータを一緒くたにして計算する

実際の業務で多クラス分類の結果をROCで評価したいことは多いです．

結構この辺りは実際に働いているデータサイエンティストの中でもわかっていない人が多いと思います．

そのため，「当たり前のように使う」のではなく「相手に説明できるようにして使う」のがベターです．

今回の内容は，本講座でも今後使っていく予定ですので，流れをしっかり覚えておきましょう！

次回から次元削減のPCA(主成分分析)という手法について解説していきます．

それでは！

追記)次回の記事書きました