データサイエンス入門の機械学習編第12回です!(講座全体の説明と目次はこちら)
今回は機械学習で最も重要な概念の一つであるBias-Variance Tradeoffについて解説していきます.
聞いたことあるという人や,一度勉強したという人も多いと思いますが,これをちゃんと理解して実務に活かせている人は多くないと思います.
この概念は非常に重要で,今後の講座の内容も基本的にはこのBias-Variance Tradeoffを意識して解説をしますし,実際に機械学習のモデルを構築する際には常にこれを意識しながらモデル構築と評価をすることになります.
目次
Bias-Variance Tradeoffとは?
なんだか英語表記で頭に入ってこないという人もいるかもしれませんが,Bias-Variance Tradeoffというのは,簡単にいうとモデルの複雑性と単純化はトレードオフの関係にあって,モデルを複雑なものにしていくと学習データに対して過学習していき,汎化性能は徐々に落ちていきますが,モデルが単純すぎると学習データに対しても汎化性能も高くすることができません.ちょうどいいモデルを構築するのが重要ということですね!
Bias-Variance Tradeoffを理解するには,モデルを複雑にしていくと学習データに対する誤差(train error)とテストデータに対する誤差(test error)がどう変わっていくのかを見るのが早いです.
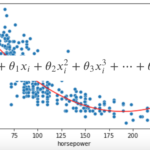
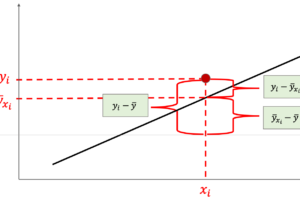
以下の図を見てください.(非常に有名な図です.機械学習をする際は常にこの図を頭に入れておいて欲しいくらい重要!!)
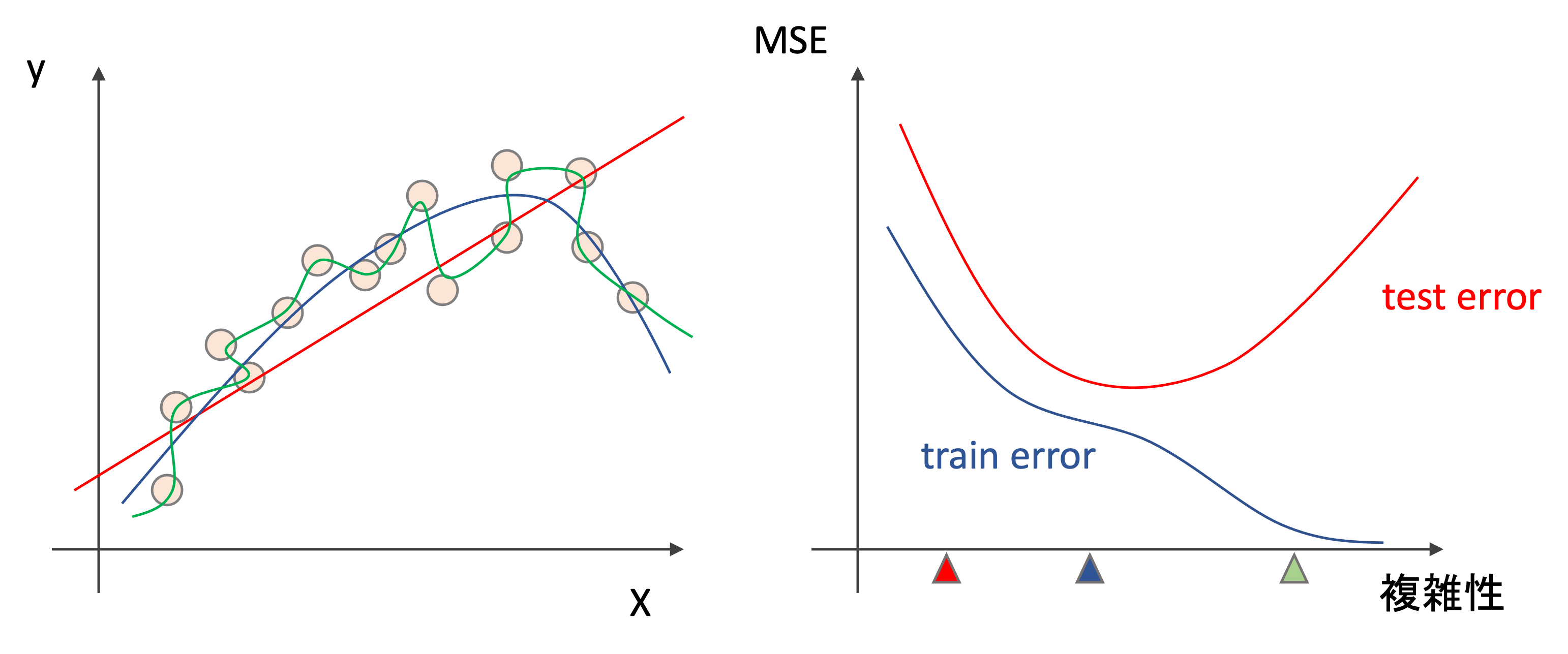
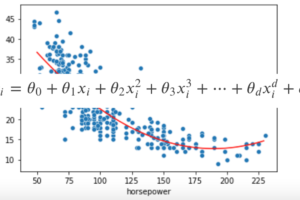
左図は,あるデータに対して三つの違ったモデルを学習させた結果です.赤は線形で,青と緑は非線形です.青は学習データに対して緩やかなカーブを描いているのに対し,緑は学習データにほぼ完全にフィットしています.
右側には,一般的なモデルの複雑性と精度(MSE)の推移です.学習データに対するMSE(赤)とテストデータに対するMSE(青)を書いています.実際に値を計測したグラフではなく,イメージ図です.

このグラフのポイントは,モデルが複雑になるにつれて最初はtrain errorとtest errorは下がっていくが,あるところからtest errorは上がっていくということ.例えば左図の緑の線のように学習データにかなりフィットすると,train errorはかなり小さくなりますが,test errorは高く,汎化性能が高いとは言えません.(これについては第7回の過学習と汎化性能のところで述べましたね)

ここで言っている”複雑性”はモデル自体の複雑性というよりは,データに複雑にフィットしているかどうかだと思ってください.(ほとんどの場合このお両者は一致しますが)英語でいうとflexibilityといい,フレキシブルに学習データにフィットしているかどうかです.線形回帰は(二次元の場合は)ただ線を引くだけなのでまったくフレキシブルではないですよね

では一体biasとvarianceとはなにを指しているのでしょうか?
Bias(偏り)とは
BIasは日本語でいうと「偏り」という意味です.日本語でもよく「バイアス」というので英語で覚えちゃいましょう.
ここでいうBiasは,「実際の問題を簡略化したことによる誤差」です.

例えば線形回帰なんかは問題を簡略化していると言えます.「広さ」から「家賃」を予測することを例にとると,本来これら二つには複雑な関係があるはずですが,それを線形と仮定してモデルを構築するのが線形回帰です.この簡略化によって何かしらの誤差(エラー)が生じると考えることができます.これがBiasです.
現実世界で本当に線形の関係のものなんてほとんどないはずなんですが,機械学習ではよく線形回帰を使います.これにはBiasの誤差が生まれると思ってください
Variance(分散)
Varianceは日本語では分散ですね.
ではこれはなんの分散を指しているのでしょうか?
答えは\(\hat{f}(x)\)の分散です.つまり\(Var(\hat{f}(x))\)ですね
\(\hat{f}(x)\)の分散が高いというのは,異なる学習データで\(\hat{f}\)を推定した時のばらつきが高いということです.
例えば線形回帰では,学習データセットを変えても\(\hat{f}\)はそんなには変わらないはずです
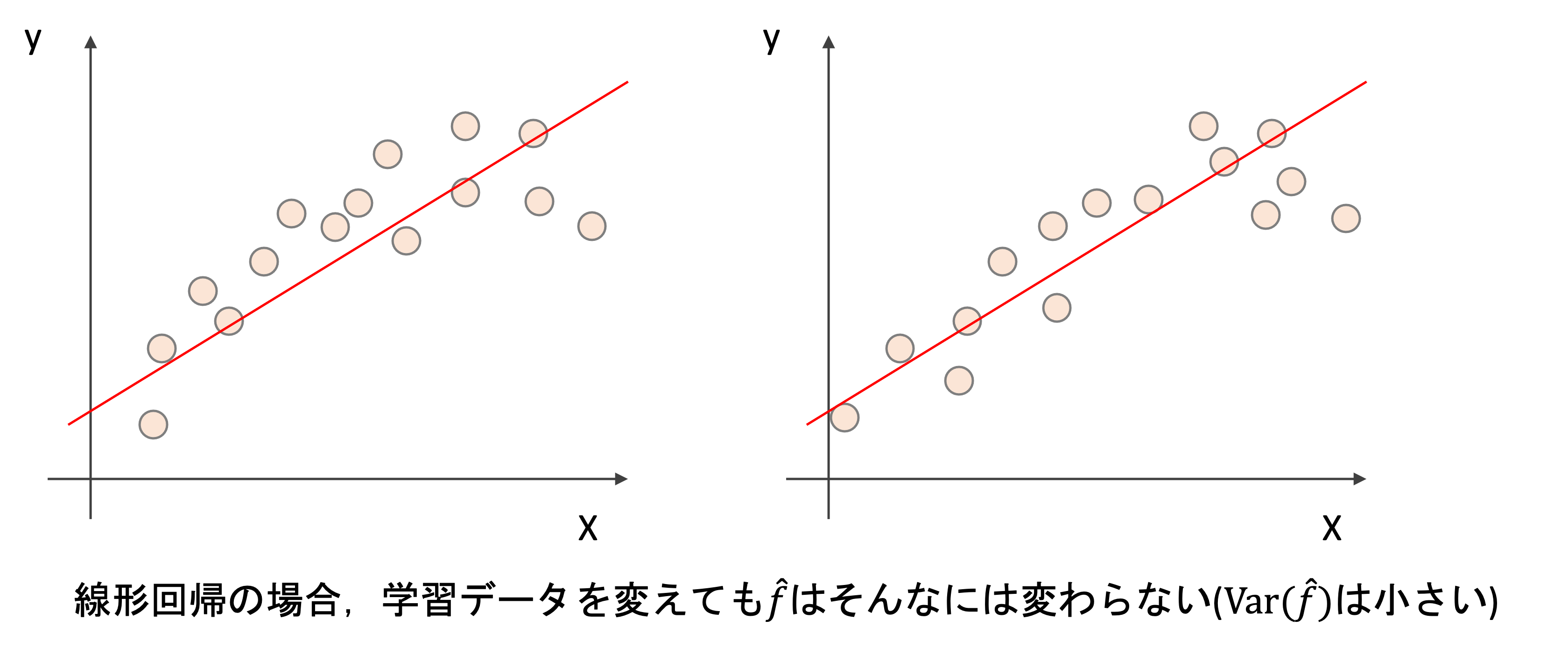
しかし,より複雑なモデルはどうでしょうか?学習データを変えるとそれだけ\(\hat{f}\)も大きく変わるのがわかると思います.
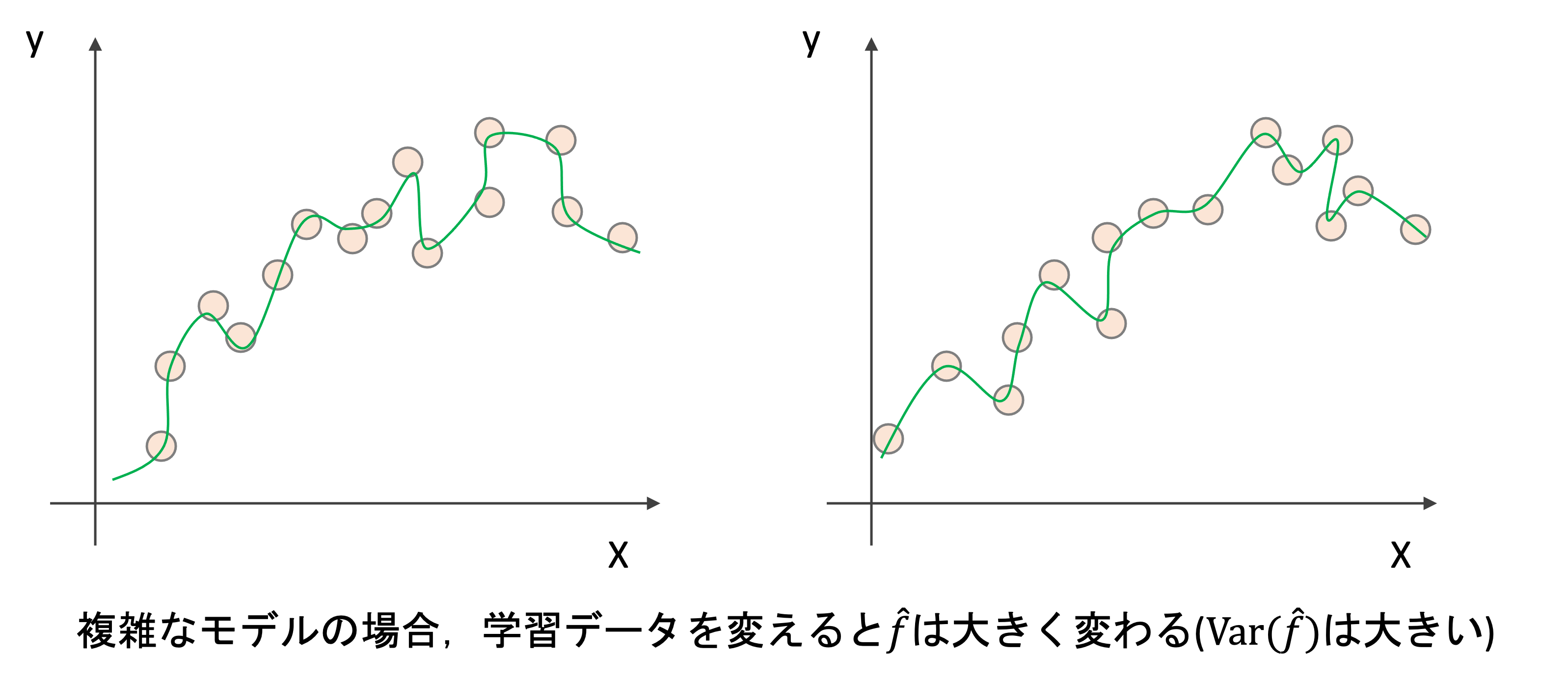
ようは,モデルが複雑になるにつれてVarianceは高くなっていくということです.本来学習データの差によって\(\hat{f}\)は変わってほしくないですよね?(「たまたま今回の学習データセットだったから得られた結果」なんてのは信頼できないわけです.)これは学習データのランダムないわばノイズを学習していることになります.

その通り! low biasでhigh varianceを得るのは簡単で,学習データに沿って線を引けばいいし,high biasでlow varianceのモデルが欲しければ,水平に直線を引けばいいわけです
汎化誤差はBiasとVarianceとエラー項に分解できる
モデルの汎化性能の誤差(汎化誤差)はBiasとVarianceとエラー項に分けることができます.
エラー項というのは,本来元々あるもので,これは小さくすることができません.これをirreducible errorと言います.
一方BiasとVarianceは小さくすることができるため,reducible errorと言います.
導出は割愛しますが,数式では以下のように表現することができます.別に覚える必要はありません.重要なのは誤差をこの三つに分解することができるということです
$$E[(y_i-\hat{f}(x_i))^2]=(Bias[\hat{f}(x_i)])^2+Var(\hat{f}(x_i))+var(\epsilon)$$
\(E[(y_i-\hat{f}(x_i))^2]\)はテストデータ\(x_i\)におけるMSEの期待値(平均)です.この式で重要なのは,テストデータにおけるMSEを下げるには,BiasとVarianceがどちらも低くなるようにしないといけないということです.また,機械学習する際には常に小さくすることができないirreducible errorの存在を頭に入れておきましょう!
BiasとVarianceの関係
実際にBiasとVarianceを明示するのは難しいのですが,イメージとしてはBiasとVarianceは以下のように推移していきます.(実際にはデータによって大きく異なりますが,イメージ図として頭に入れておきましょう!)
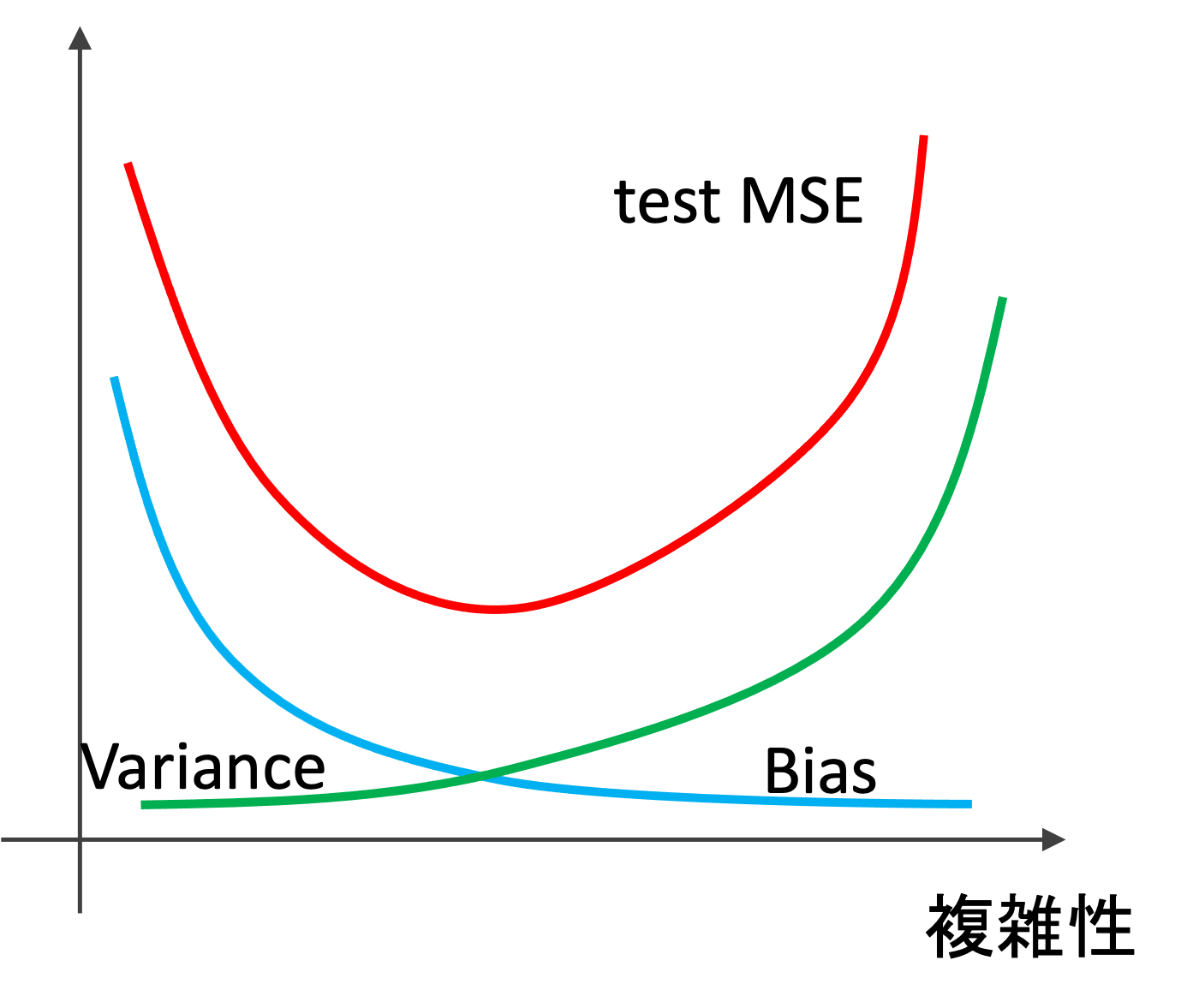
複雑性を上げていくと,Varianceの増加よりも早くBiasが下がっていくので,test MSEは下がりますが,ある点を超えるとBiasの下がりよりもVarianceが急にあがりtest MSEも上がっていく感じです.

Bias-Variance Tradeoffの使い所
Bias-Variance Tradeoffは,機械学習において最も重要な概念と言えるくらい,様々なところで出てきます.本講座でも今後Bias-Variance Tradeoffを参照する記事は多くなります.
でも,具体的にどうモデル構築に活かせるのか気になりますよね!一般的な見方と考え方をここでは紹介してきます.
機械学習のモデルを構築する際には,どのパラメータの値が精度の高いモデルになるのかわからないので,色々なパラメータの値を試してモデル構築をします.(このパラメータのことをハイパーパラメータと言います)
モデルの複雑性もこのハイパーパラメターの一種です.例えば多項式回帰の次元\(d\)もまさにハイパーパラメータですよね.
例えばd=0からd=10までのモデルを構築して,それぞれのtrain MSEとtest MSE(通常はk-Fold CVのMSE)を見ることで,今High BiasなのかHigh Varianceなのかを確認することができます.
例えば
- test errorもtrain errorも高い→Biasの問題なので次元を上げたり特徴量を増やす.データを増やしてもtest errorは下がらない場合が多い
- test errorは高いがtrain errorは低い→Varianceの問題なので次元を下げたり特徴量を減らす.またデータを増やすことで解決する場合もある
このように,今high biasなのかhigh varianceなのかがわかれば,学習データを増やすべきなのか特徴量を増やすべきなのかがわかるので,無駄な労力をかけることがなくなるかも知れません.
他にも,今後紹介する特徴量選択アルゴリズムの正則化のパラメータも,このBias-Variance Tradeoffをみて最適なパラメータを調べたりします.この辺りはまた解説していきます.
まとめ
今回はBias-Variance Tradeoffについて解説しました.Bias-Variance Tradeoffは機械学習で最も重要な概念の一つです.この機械学習のブログ講座でも最も重要な記事の一つだと思います.今後色々なところでこの記事を参照するようになるでしょう!
- 汎化誤差はBiasとVarianceとエラー項に分解される
- BiasとVarianceはどちらもreducible errorであり,これらを下げることが精度向上となる.
- BiasとVarianceはトレードオフの関係にあるので,片方を下げるともう片方が上がる.
- Biasは複雑な問題を簡略化したことによるエラー.線形回帰などのシンプルなモデルではBiasが大きい
- Varianceは学習データを変えた時のモデルの分散.複雑なモデルであるほどVarianceは大きい
- 学習したモデルがHigh BiasなのかHigh Varianceなのかを見極めることで,なにをすればいいのかがわかる
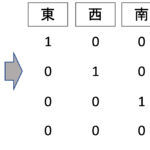
それでは,次回の記事では質的変数を特徴量として使う際の特徴量変換について解説します!
今までは量的変数(連続変数)のみ特徴量として扱ってましたが,実際に特徴量として使いたいデータには,質的変数も含まれますよね?それについてどうすれば回帰モデルの特徴量として使えるのかを解説していきます!
それでは!
追記)次回の記事書きました!