(追記)全16時間の統計学動画講座を公開しました!☆4.8の超高評価をいただいている講座です.こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください.
データサイエンス入門:統計講座第31回です.
今回は連関の検定をやっていきます.連関というのは,質的変数(カテゴリー変数)における相関だと思ってください.(相関については第11回あたりで解説しています)
例えば, 100人の学生に「データサイエンティストを目指しているか」と「Pythonを勉強しているか」という二つの質問をした結果,以下のような表になったとします.
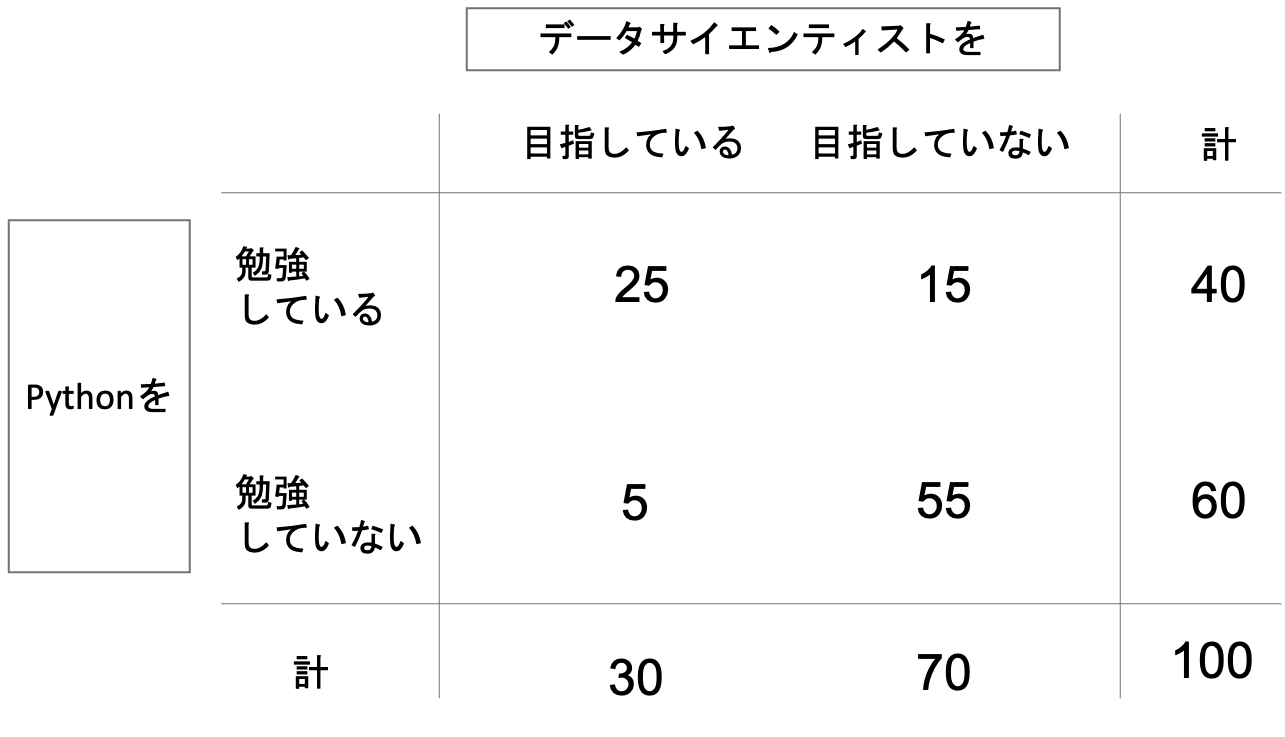
このように,質的変数のそれぞれの組み合わせの集計値(これを度数と言います.)を表にしたものを,分割表やクロス表と言います.英語でcontingency tableともいい,日本語でもコンティンジェンシー表といったりするので,英語名でも是非覚えておきましょう.
連関(association)というのは,この二つの質的変数の相互関係を意味します.表を見るに,データサイエンティストを目指す学生40名のうち,25名がPythonを学習していることになるので,これらの質的変数の間には連関があると言えそうです.(逆に連関がないことを,独立していると言います.)
連関の検定では,これらの質的変数間に連関があるかどうかを検定します.(言い換えると,質的変数間が独立かどうかを検定するとも言え,連関の検定は独立性の検定と呼ばれたりもします.)
目次
帰無仮説は「差はない」(=連関はない,独立である)
比率の差の検定同様,連関の検定も「差はない」つまり,「連関はない,独立である」という帰無仮説を立て,これを棄却することで「連関がある」という対立仮説を成立させることができます.
もし連関がない場合,先ほどの表は,以下のようになるかと思います.
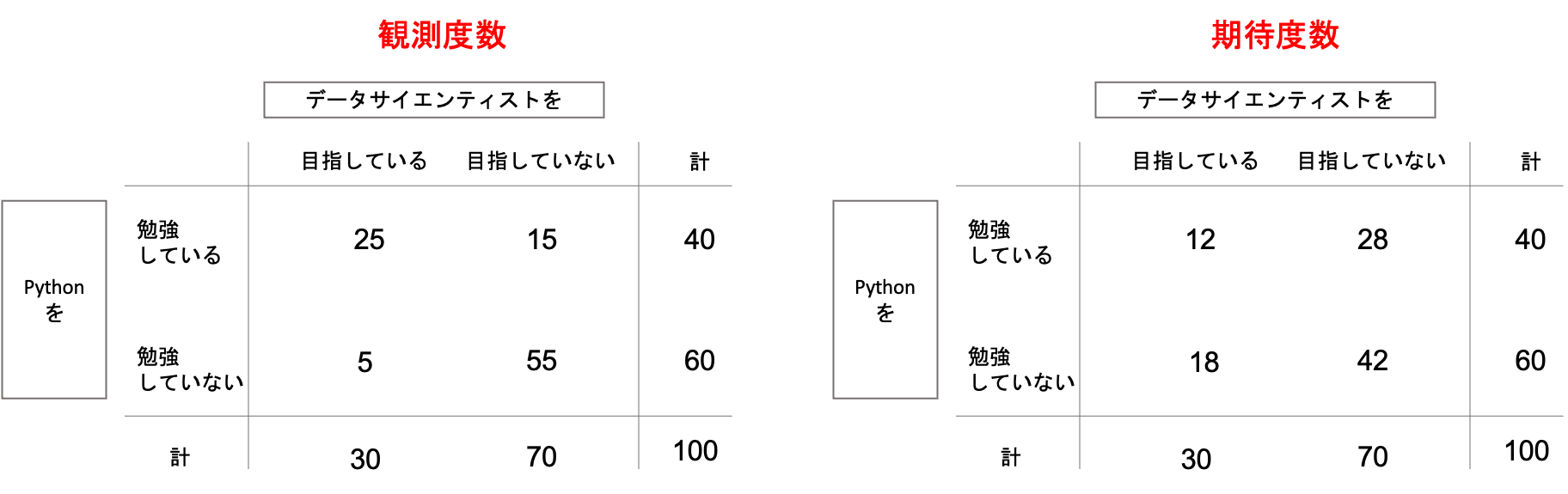
左の表が実際に観測された度数(観測度数)の分割表で,右の表がそれぞれの変数が独立であると想定した場合に期待される度数(期待度数)の分割表です.
もしデータサイエンティストを目指しているかどうかとPythonを勉強しているかどうかが関係ないとしたら,右側のような分割表になるよね,というわけです.
データサイエンティストを目指している30名と目指していない70名の中で,Pythonを勉強している/していないの比率が同じになっているのがわかると思います.
つまり「帰無仮説が正しいとすると右表の期待度数の分割表になるんだけど,今回得られた分割表は,たまたまなのか,それとも有意差があるのか」を調べることになります.

その通り.今回の例でいうと,Pythonを勉強しているかどうかの比率が,データサイエンティストを目指しているかどうかによって異なるかどうかを調べていると考えると,分割表が2×2の場合,やっている分析は比率の差の検定(Z検定)と同じになります.(後ほどこれについては詳しく説明します.)
観測度数と期待度数の差を検定する
帰無仮説は「連関がない」なので,今回得られた値がたまたまなのかどうかを調べるのには,先述した観測度数と期待度数の差を調べ,それが統計的に有意なのかどうか見ればいいですね.
では,どのようにこの”差”を調べればいいでしょうか?
普通に差をとって足し合わせると,プラスマイナスが打ち消しあって0になってしまいます.
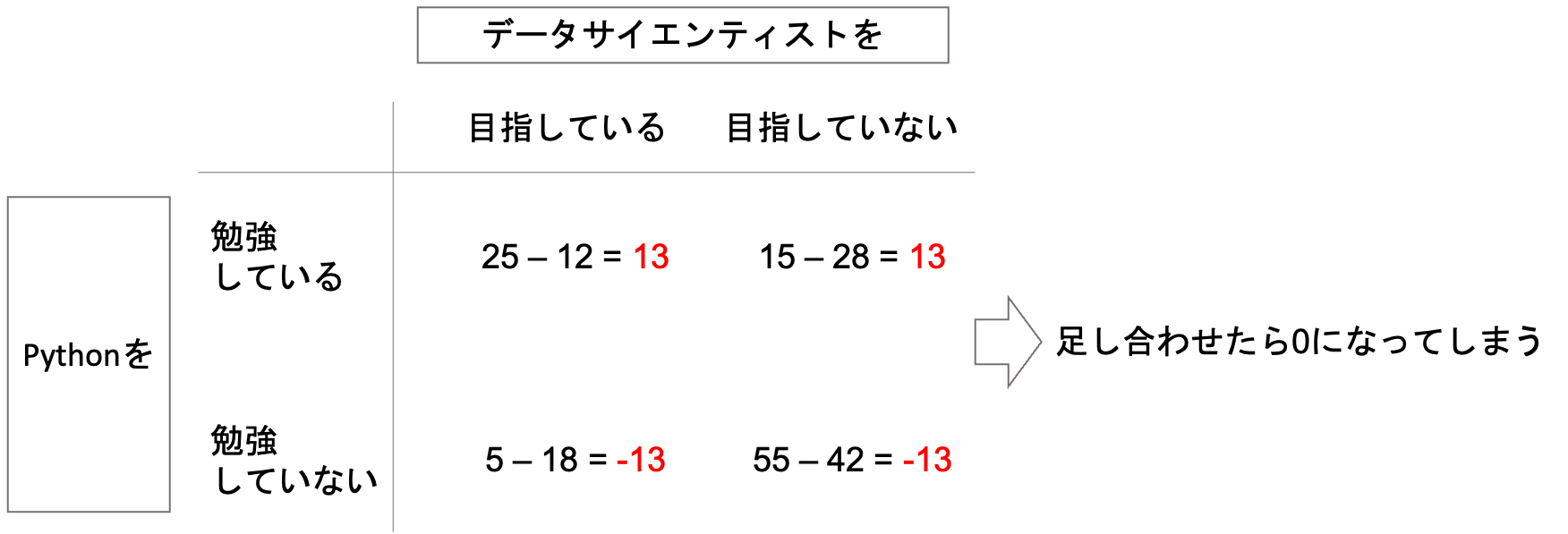
これを避けるために,二乗した総和にしてみましょう.(絶対値を使うのではなく,二乗をとった方が何かと扱いやすいという話を第5回でしました.)
すると,差の絶対値が全て13なので,二乗の総和は\(13^2\times4=676\)になります.(考え方は第5回で説明した分散と同じですね!)

そう,この値もどんどん大きくなってしまいます.なので,標準化的なものが必要になっています.そこで,それぞれの差の二乗を期待度数で割った数字を足していきます.
イメージとしては,ズレが期待度数に対してどれくらいの割合なのかを足していくイメージです.そうすれば,対象が100人だろうと1000人だろうと同じようにその値を扱えます.

この\((観測度数-期待度数)^2/期待度数\)の総和値を\(\chi^2\)(カイ二乗)統計量と言います.(変な名前のようですが覚えてしまいましょう!)
数式で書くと以下のようになります.(\(a\)行\(b\)列の分割表における\(i\)行\(j\)列の観測度数が\(n_{ij}\),期待度数が\(e_{ij}\)とすると
$$\chi^2=\sum^{a}_{i=1}\sum^{b}_{j=1}\frac{(n_{ij}-e_{ij})^2}{e_{ij}}$$
となります.式をみると難しそうですが,やってることは単純な計算ですよね?
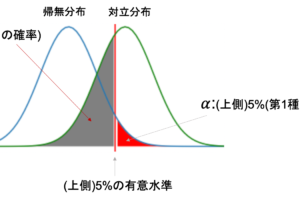
そして\(\chi^2\)が従う確率分布を\(\chi^2\)分布といい,その分布から,今回の標本で計算された\(\chi^2\)がどれくらいの確率で得られる値なのかを見ればいいわけです.
連関の検定は,\(\chi^2\)(カイ二乗)統計量を使って検定をするので\(\chi^2\)(カイ二乗)検定とも呼ばれます.(こちらの方が一般的かと思います.)
\(\chi^2\)分布をみてみよう
では先ほど求めた\(\chi^2\)がどのような確率分布をとるのかみてみましょう.\(\chi^2\)分布は少し複雑な確率分布なので,簡単に数式で表せるものではありません.
なので,今回もPythonのstatsモジュールを使って描画してみます.
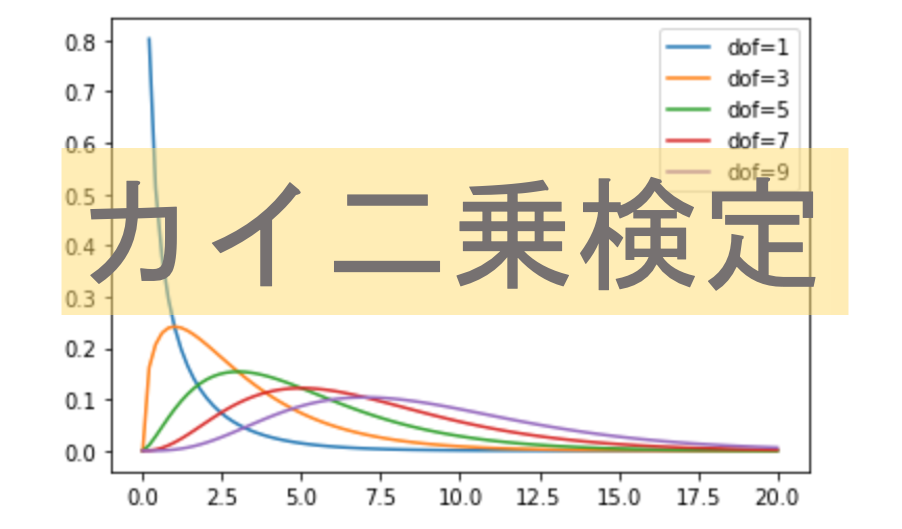
と,その前に一点.\(\chi^2\)分布は唯一「自由度(degree of freedom)」というパラメータを持ちます.(t分布も,自由度によって分布の形状が変わっていましたね)
\(\chi^2\)分布の自由度は,\(a\)行\(b\)列の分割表の場合\((a-1)(b-1)\)になります.
つまりは\(2\times2\)の分割表なので\((2-1)(2-1)=1\)で,自由度=1です.
例えば今回の場合,「Pythonを勉強している/していない」という変数において,「Pythonを勉強している人数」が決まれば「していない」人数は自動的に決まります.つまり自由に決められるのは一つであり,自由度が1であるというイメージができると思います.同様にとりうる値が3つ,4つ,と増えていけば,その数から1を引いた数だけ自由に決めることができるわけです.行・列に対してそれぞれ同じ考えを適用していくと,自由度の式が\((a-1)(b-1)\)になるのは理解できるのではないかと思います.
それでは実際にstatsモジュールを使って\(\chi^2\)分布を描画してみます.\(\chi^2\)分布を描画するにはstatsモジュールの chi2 を使います.
使い方は,他の確率分布の時と同じく, .pdf(x, df) メソッドを呼べばOKです. .pdf() メソッドにはxの値と,自由度 df を渡しましょう.(.pdf()メソッドについては第21回や第22回などでも出てきていますね)
いつも通り, np.linespace() を使ってx軸の値を作り, range() 関数を使ってfor文で自由度を変更して描画してみましょう.(np.linespace()については「データサイエンスのためのPython講座」の第8回を参考にしてください)
|
1 2 3 4 5 6 7 8 9 10 11 |
import numpy as np import matplotlib.pyplot as plt from scipy.stats import chi2 %matplotlib inline x = np.linspace(0, 20, 100) for df in range(1, 10, 2): y = chi2.pdf(x, df=df) plt.plot(x, y, label=f'dof={df}') plt.legend() |
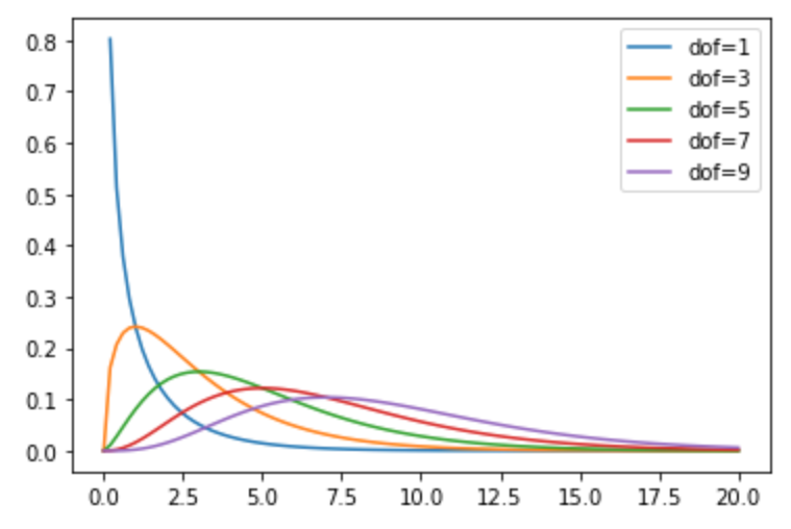
今回は,自由度( df 引数)に1, 3, 5, 7, 9を入れて\(\chi^2\)分布を描画してみました.自由度によって大きく形状が異なるのがわかると思います.
実際に検定をしてみよう!
今回は\(2\times2\)の分割表なので,自由度は\((2-1)(2-1)=1\)となり,自由度1の\(\chi^2\)分布において,今回算出した\(\chi^2\)統計量(35.53)が棄却域に入るのかをみれば良いことになります.
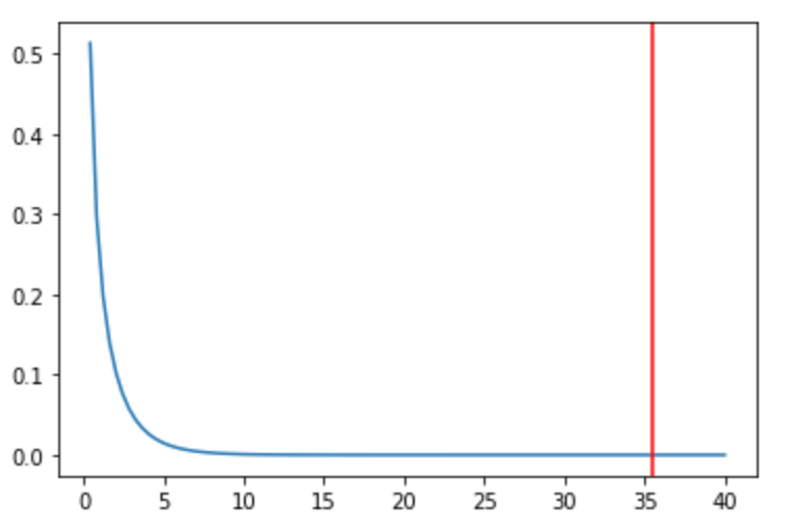
第28回の比率の差の検定同様,有意水準を5%に設定します.
自由度1の\(\chi^2\)分布における有意水準5%に対応する値は3.84です.連関の検定の多くは\(2\times2\)の分割表なので,余裕があったら覚えておくといいと思います.(標準正規分布における1.96や1.64よりは重要ではないです.)
なので,今回の\(\chi^2\)値は有意水準5%の3.84よりも大きい数字となるので,余裕で棄却域に入るわけですね.
つまり今回の例では,「データサイエンティストを目指している/目指していない」の変数と「Pythonを勉強している/していない」の変数の間には連関があると言えるわけです.
実際には統計ツールを使って簡単に検定を行うことができます.今回もPythonを使って連関の検定(カイ二乗検定)をやってみましょう!
Pythonでカイ二乗検定を行う場合は,statsモジュールのchi2_contingency()メソッドを使います.
chi2_contingency() には observed 引数と, correction 引数を入れます. observed 引数は観測された分割表を多重リストの形で渡せばOKです. correction 引数はbooleanの値をとり,普通のカイ二乗検定をしたい場合は False を指定してください.stats.chi2_contingency() はデフォルトでイェイツの修正(Yates’s correction)なるものがされます.これは,サンプルサイズが小さい場合に\(\chi^2\)値を小さくし,p値が高くなるように修正をするものですが,用途は限られるため,普通にカイ二乗検定をする場合は correction=False を指定すればOKです.
|
1 2 3 |
from scipy.stats import chi2_contingency obs = [[25, 15], [5, 55]] chi2_contingency(obs, correction=False) |
|
1 2 3 4 5 |
(33.53174603174603, 7.0110272972619556e-09, 1, array([[12., 28.], [18., 42.]])) |
めちゃくちゃ便利ですね.p値をみると<0.05であることがわかるので,今回の変数間には連関があると言えるわけです.
比率の差の検定は,カイ二乗検定の自由度1のケース
先述したとおりですが,比率の差の検定は,実はカイ二乗検定の自由度1のケースです.
第28回の例を stats.chi2_contingency() を使って検定をしてみましょう.第28回の例は以下のような分割表と考えることができます.(問題設定は,「生産過程の変更前後で不良品率は変わるか」です.詳細は第28回を参照ください.)
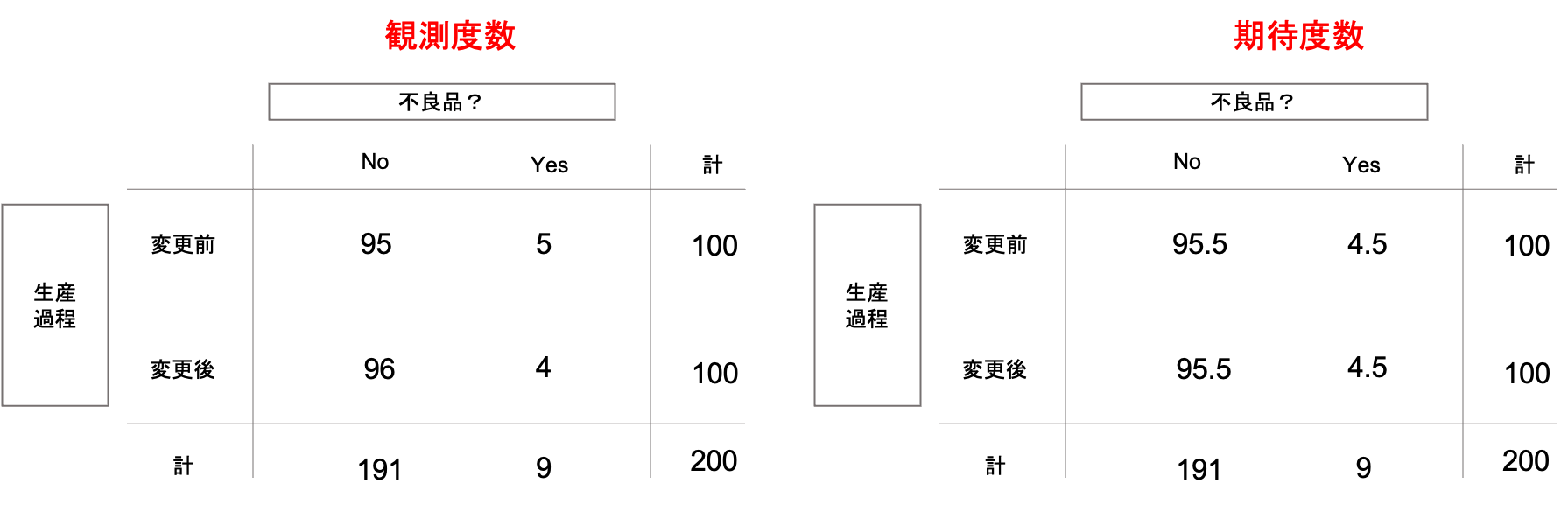
|
1 2 3 |
from scipy.stats import chi2_contingency obs = [[95, 5], [96, 4]] chi2_contingency(obs, correction=False) |
|
1 2 3 4 5 |
(0.11634671320535195, 0.7330310563999259, 1, array([[95.5, 4.5], [95.5, 4.5]])) |
結果を見ると,p値は0.73であることがわかります.これは,第28回で紹介した statsmodels.stats.proportion.proportions_ztest() メソッドで有意水準0.5%における両側検定をしたときのp値と同じ結果です.
|
1 2 |
from statsmodels.stats.proportion import proportions_ztest proportions_ztest([5, 4], [100, 100], alternative='two-sided') |
|
1 |
(0.34109634006443396, 0.7330310563999258) |
このように,比率の差の検定は自由度1のカイ二乗検定の結果と同じになります.
しかし,カイ二乗検定では,比率が上がったのか下がったのか,つまり比率の差の検定における片側検定をすることはできません.(これは,\(\chi^2\)値が差の二乗から計算され,負の値を取らないことからもわかるかと思います.観測度数が期待度数通りの場合,\(\chi^2\)値は0ですからね.常に片側しかありません.)
そのため,比率の差の検定をする際は stats.chi2_contingency() よりも何かと使い勝手の良い statsmodels.stats.proportion.proportions_ztest() を使うと◎です.
まとめ
今回は現実問題でもよく出てくる連関の検定(カイ二乗検定)について解説をしました.
- 連関は,質的変数における相関のこと
- 質的変数のそれぞれの組み合わせの度数を表にしたものを分割表やクロス表という(contingency table)
- 連関の検定は,変数間に連関があるのか(互いに独立か)を検定する
- 帰無仮説は「連関がない(独立)」
- 統計量には\(\chi^2\)(カイ二乗)統計量(\((観測度数-期待度数)^2/期待度数\)の総和)を使う
- \(\chi^2\)分布は自由度をパラメータにとる確率分布(自由度は\(a\)行\(b\)列の分割表における\((a-1)(b-1)\))
- Pythonでカイ二乗検定をするには stats.chi2_contingency() を使う
- 比率の差の検定は,自由度1のカイ二乗検定と同じ分析をしている
今回も盛りだくさんでした...
カイ二乗検定はビジネスの世界でも実際によく使う検定なので,是非押さえておきましょう!
次回は検定の中でも最もメジャーと言える「平均値の差の検定」をやっていこうと思います!今までの内容を理解していたら簡単に理解できると思うので,是非第28回と今回の記事をしっかり押さえた上で進めてください!
それでは!
追記)次回の記事書きました!