前回の記事では,損失関数というものを導入し,損失が最小になるようなパラメータを見つけるアルゴリズムの一つとして,最急降下法というものを紹介しました.(講座全体の説明と目次はこちら)
それでは,実際にどのようにこの最急降下法を使って求めれるのでしょうか?このアルゴリズムをうまく数式で表し,どのように計算していくのかをみてみましょう!
追記)機械学習超入門動画講座を公開しました!動画で効率よく学習をしたい人はこちら(現在割引クーポン配布中です)
目次
数式を使って最急降下法を表してみる

これには微分を使います.機械学習では微分が頻出してきますが,本講座では「微分なんて分からないよ〜」という人でも理解できるようにやさしく書いていきますね!

それは,その地点での接線の傾きの係数を微分で求めることができるからです.その傾きの係数がわかれば,その方向にパラメータを少しだけ動かすことができますよね?
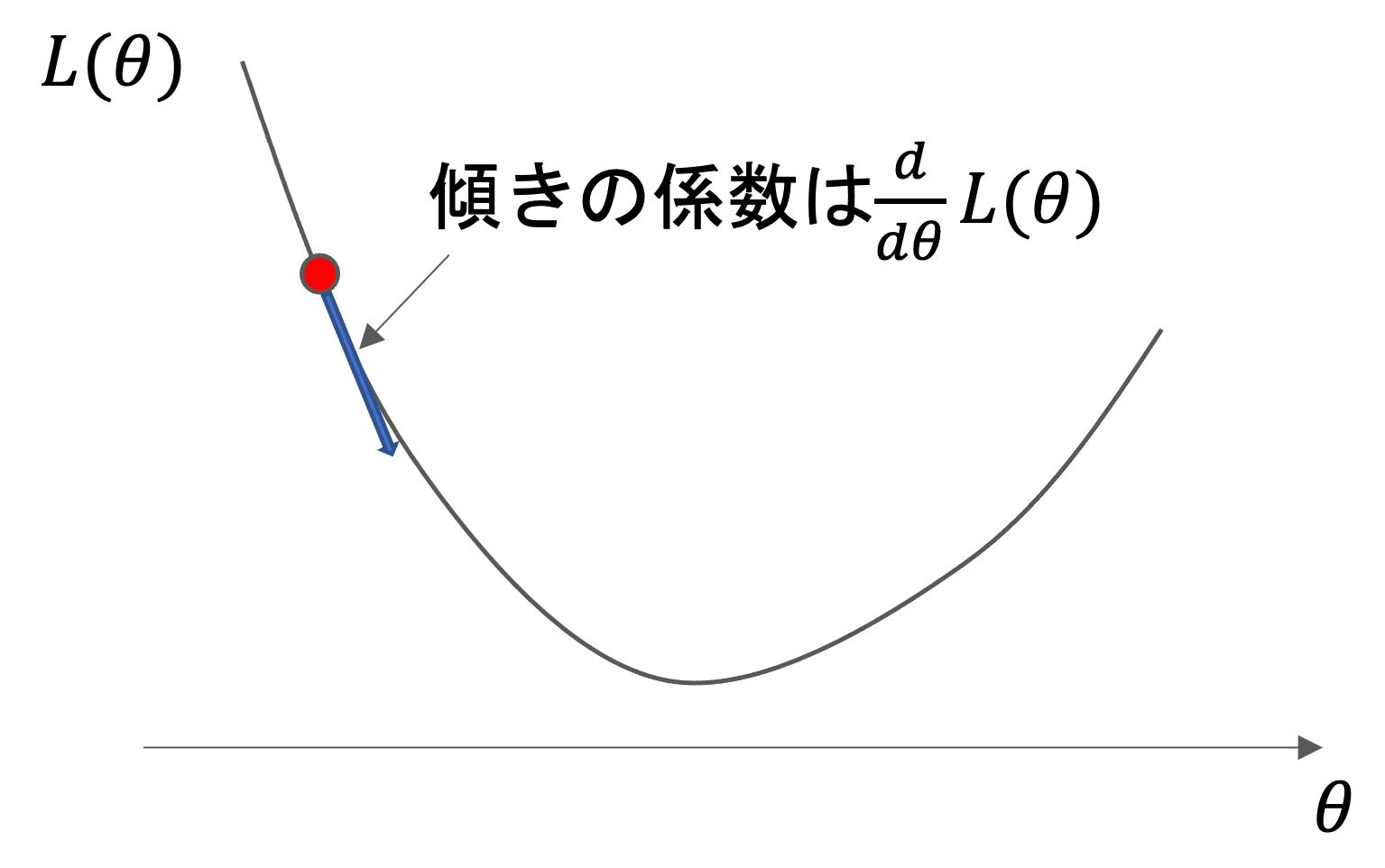
例えば,\(y=x^2\)のグラフをみてみましょう.ある地点\(x’\)の接線の傾きは,yをxで微分した\(\frac{d}{dx}y=2x\)に\(x=x’\)を代入した値になりますよね?
機械学習ではどうしても微積(微分と積分)が必要になってきます.微分の公式などを最初からできるようにする必要はないかもしれませんが,学習を進めていく中で徐々に並行して微積の知識をつけいてきましょう.おすすめの本をこちらの記事で紹介しているので是非参考にしてみてください.
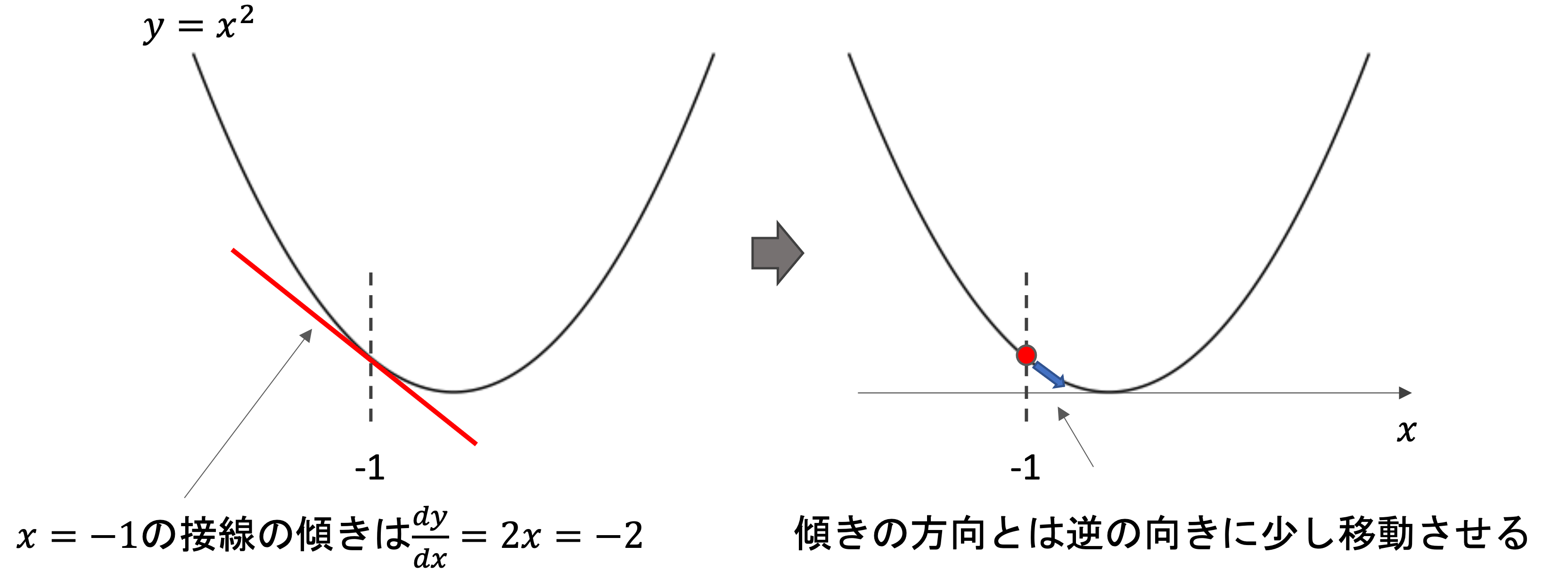
例えばx=-1の地点における接線の傾きは-2です.これを左上方向(マイナスの方向)に2という大きさを持ったベクトルを考えてみてください(このようなベクトルを勾配ベクトルと言います)
この勾配ベクトルとは逆の向きに点を動かしていきます.(最小地点に辿り着きたいので,坂の勾配の逆をいく必要があるからです.また,実際に動かすのはパラメータの\(x\)なので,向きは正負の2方向のみです.ベクトルの大きさが,変動の大きさになります)
これを繰り返すと徐々に傾きが小さくなっていき,点の移動が徐々に小さくなりやがては傾き0の地点になり,点が動かなくなるのがわかると思います.(実際には,その0の地点に辿り着くのではなく,徐々に移動が小さくなりほぼほぼ動かないところで止めます)
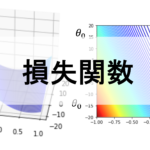
\(\theta\)というパラメータ一つだけの損失関数を考えると,これは以下のように書くことができます.
$$\theta := \theta – \alpha \frac{d}{d\theta}L(\theta)$$
損失関数を\(\theta\)で微分した\(\frac{d}{d\theta}L(\theta)\)を\(\theta\)から引いた値を\(\theta\)に代入していきます.(「:=」は「代入」の意味.a:=bは,bをaに代入するということ)
そのまま引いてしまうと調整が効かないので,係数\(\alpha\)をかけてあげましょう.\(\alpha\)を大きくすれば毎回の変動が大きくなり,早く解に辿り着くことができるかもしれません.逆に小さくすると,変動が小さくなり収束に時間がかかります.この\(\alpha\)のことを学習率(learning rate)と言い,学習をする際の重要なハイパーパラメータです.(どのように値を決めるかなどは今後の記事で書いていきます.今はひとまず,学習スピードを調整するパラメータだと思っておけばOKです!)
例えば\(y=x^2\)の例をみると,x=−1の接線の傾きは−2なので\(\alpha=0.05\)とすると,次のxは-1-0.05(-2)=-0.9となり,x=-0.9の傾きは-1.8なので次のxは-0.9-0.05(-1.8)=-0.81となり,x=-0.81の傾きは-1.62となり,,,と繰り返していき,いずれ最適解\(x=0\)付近に収束します.
もし変数が複数ある場合(例えば\(\theta_0\)と\(\theta_1\)は,以下のようにそれぞれの変数を”同時に”更新していけばOKです!
$$\theta_0 := \theta_0 – \alpha\frac{\partial}{\partial\theta_0}L(\theta_0, \theta_1)$$
$$\theta_1 := \theta_1 – \alpha\frac{\partial}{\partial\theta_1}L(\theta_0, \theta_1)$$

変数が二つ以上になると,偏微分となり\(d\)ではなく\(\partial\)(パーシャル)を使いますが,あまり気にしなくてOKです.微分する対象ではない方の変数は定数として扱うだけです.
例えば線形回帰の場合,損失関数は\(L(\theta_0, \theta_1)=\frac{1}{m}\sum^{m}_{i=1}(y_i-(\theta_0+\theta_1x_i))^2\)なので,これを\(\theta_0\)で偏微分した\(\frac{\partial}{\partial\theta_0}L(\theta_0, \theta_1)\)と,\(\theta_1\)で偏微分した\(\frac{\partial}{\partial\theta_1}L(\theta_0, \theta_1)\)は以下のようになります.
$$\frac{\partial}{\partial\theta_0}L(\theta_0, \theta_1)=-\frac{2}{m}\sum^{m}_{i=1}(y_i-(\theta_0+\theta_1x_i))=\frac{2}{m}\sum^{m}_{i=1}(\theta_0+\theta_1x_i-y_i)$$
$$\frac{\partial}{\partial\theta_1}L(\theta_0, \theta_1)=-\frac{2}{m}\sum^{m}_{i=1}(y_i-(\theta_0+\theta_1x_i))x_i=\frac{2}{m}\sum^{m}_{i=1}(\theta_0+\theta_1x_i-y_i)x_i$$

ぱっと見なかなかイカツイ感じに見えますが,やってることは難しくないです.合成関数の微分の公式\(\lbrace f(g(x)\rbrace’=f'(g(x))g'(x)\)がわかれば理解できます.
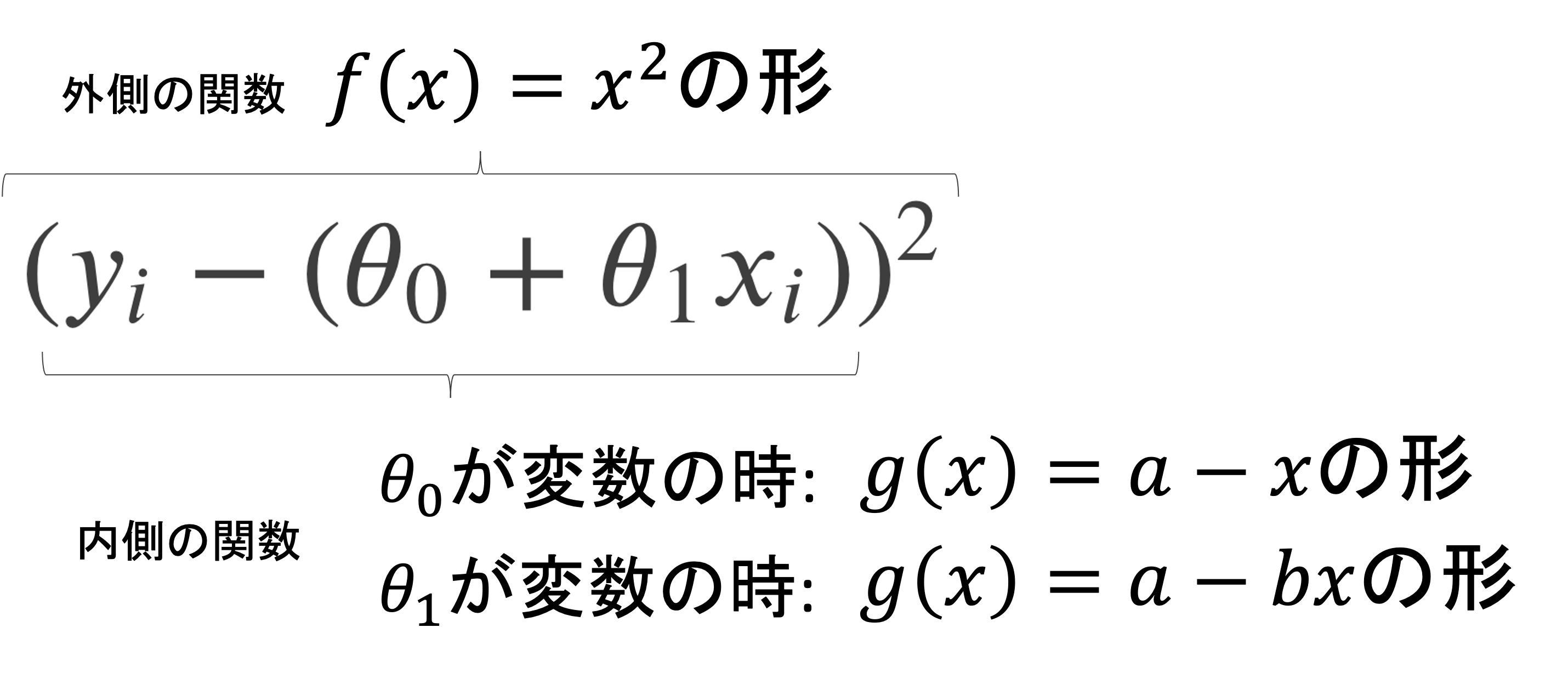
このように考えれば,先ほどの式になることがイメージできるのではないでしょうか?\(\theta_0\)での偏微分は,係数が-1なので\(g'(\theta_0)=-1\)となり,\(\theta_1\)での偏微分は,係数\(-x_i\)があるので\(g'(\theta_1)=-x_i\)となることに注意しましょう.また,マイナスが出てしまってみにくくなるので,その分\(y_i\)と\(\theta_0+\theta_1x_i\)を逆にすることで数式がスッキリします.
これを実際に前回のレクチャーの10件のデータに適用すると,\(\theta_0\)と\(\theta_1\)と損失\(L(\theta_0, \theta_1)\)は以下のように推移していきます.
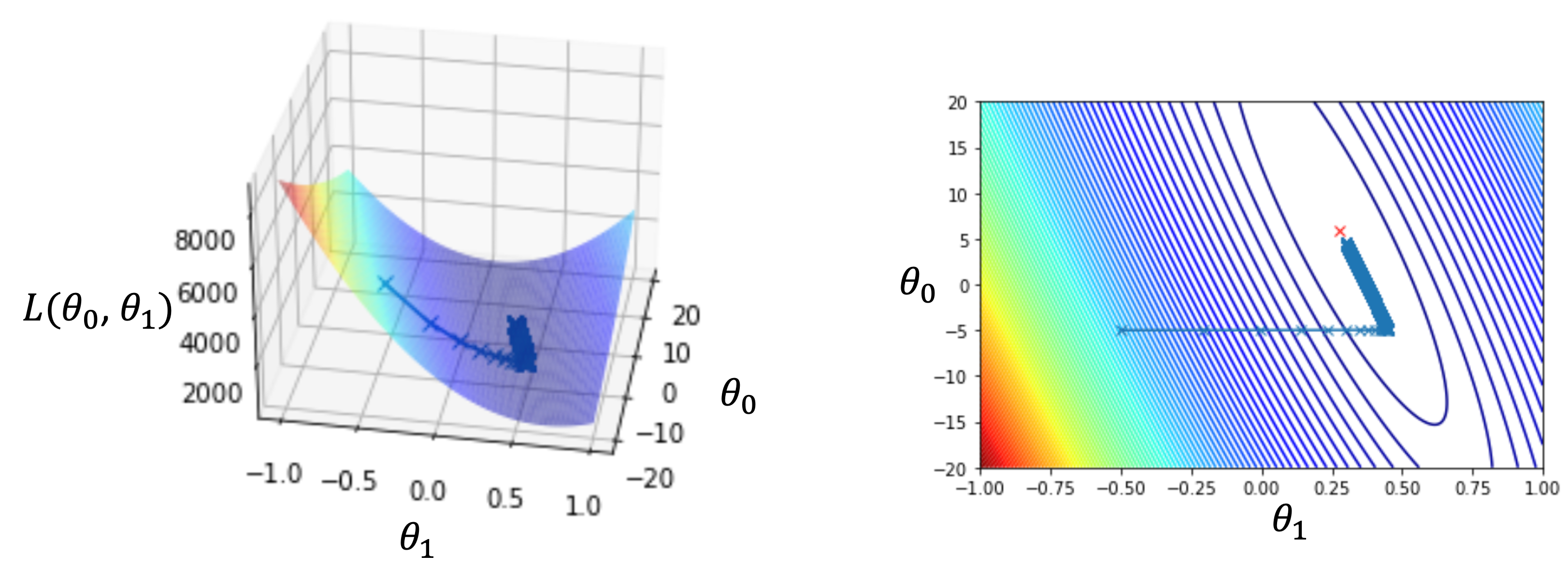
最初の点\((\theta_0,\theta_1)=(-5, -0.5)\)から徐々に最適解に移動していってるのがわかると思います.(こちらは\(\alpha=0.00005とし10万回反復した例です.\)
今回の場合は\(\theta_0=4.65\),\(\theta_1=0.3\)という結果になりましたが,これをもっと長く繰り返せば,いずれ最適解の\(\theta_0=5.92\),\(\theta_1=0.28\)に限りなく近づいていきます.
つまり,今回の最急降下法で以下のような線形回帰(\(\hat{f}(x)=4.65+0.3x\))のモデルを構築することができたわけです.
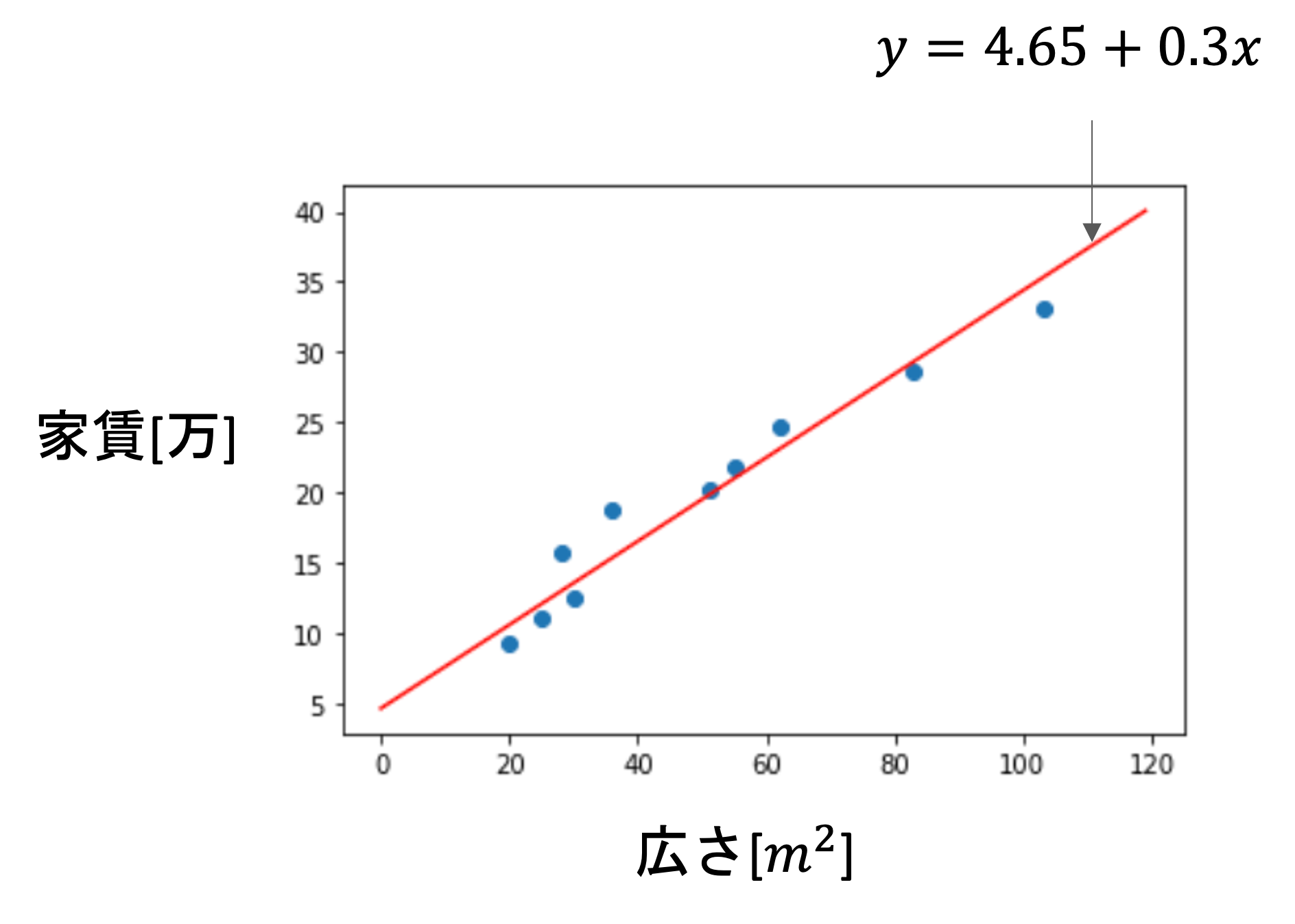
これが最急降下法によって最適解を求めるアルゴリズムの概要です!実際にはPythonにはscikit-learnという機械学習のためのライブラリがあって,線形回帰であればそれ用の関数が用意されているので,細かい実装は不要でその関数を実行すれば答えがでます.(実装についてはまた次の記事で紹介したいと思います!)
初見で理解するのは難しいと思いますが,100%理解しようとせず,まずは概要を把握し徐々に慣れていきましょう!
最急降下法の注意点

実は最急降下法にはいくつか注意点があります.ここでは代表的なものを2つ紹介します
1. 最適解(global optima)ではなく局所解(local optima)に辿り着くことも
損失関数の形が以下のようになっている場合(今後のアルゴリズムではよくあります),必ずしも最適解に辿り着くとは限らず,途中の解(これを局所解という)に辿り着いてしまい,そこで学習が終わってしまうことがあります.
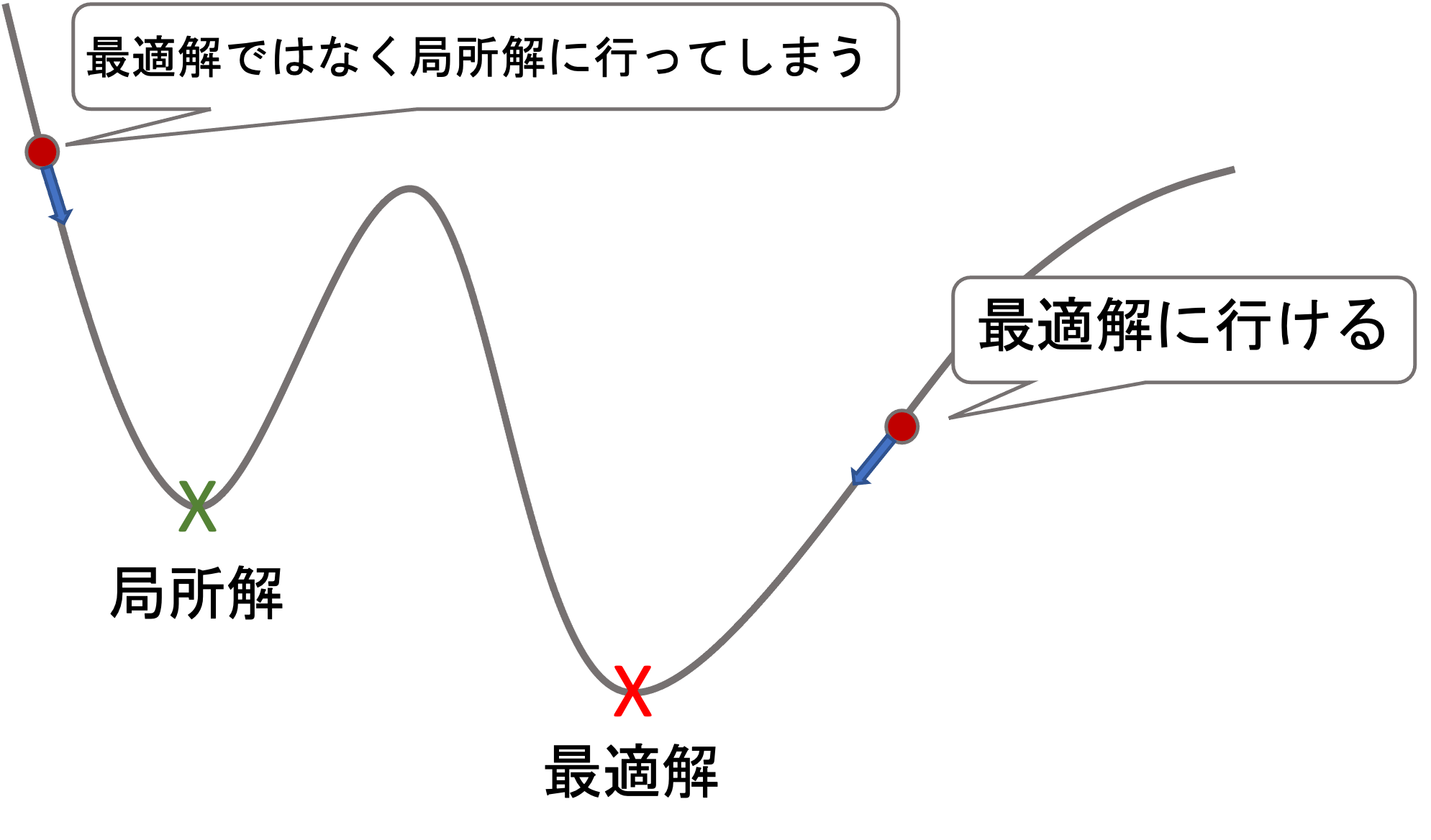
これは最初のパラメータをどこに取るかで変わってきてしまいますが,それは通常ランダムで設定するのでこれを回避するために何度か初期値を変えて学習をして,損失が最小のところを見つけることになります.(つまり,最適解かどうかは実際には分からず,最も最小の局所解を使うことになります)
2. 学習率(\(\alpha\))が大きすぎると,発散して学習が進まない
学習率\(\alpha\)が大きすぎると,一回のパラメータの変動が大きくなってしまい,収束しません.
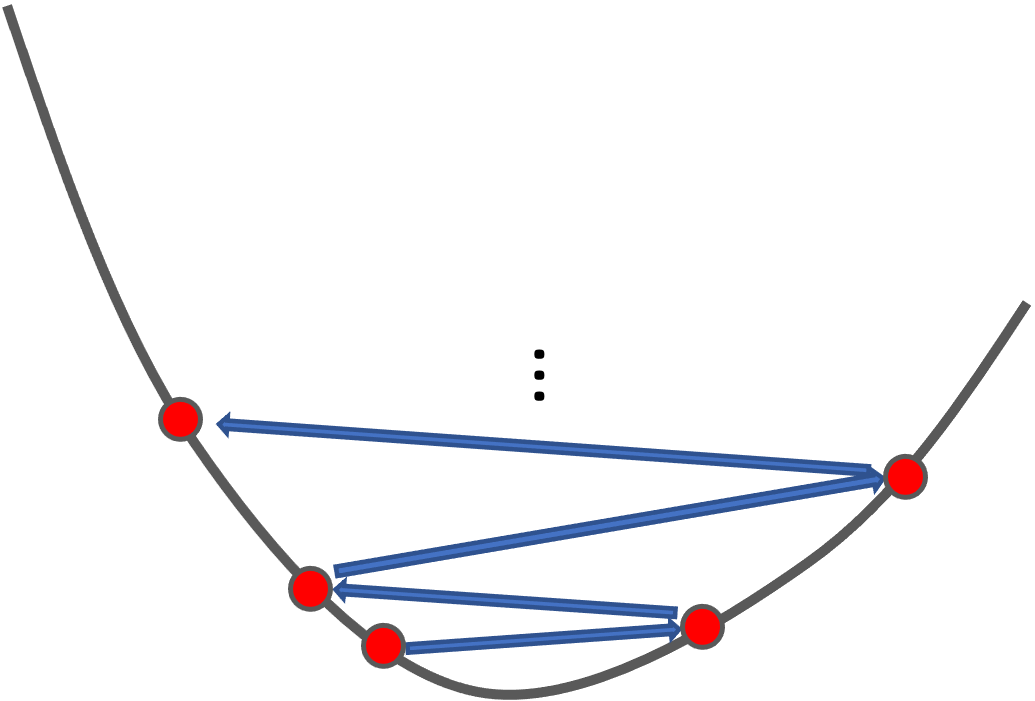
これは学習の結果や過程をみて収束しているのか発散しているのかを判断し適切な学習率を探していきます.(※逆に小さすぎると学習が進まないという問題が起こるので,小さすぎてもだめなんです)
この辺りについてはまた今後の講座記事で紹介していきたいと思います.
まとめ
今回の記事では,具体的に最急降下法を使って解を求める方法を紹介してきました!
- 勾配ベクトルを使って,それとは逆向きにパラメータを変動させる
- 初期値によっては最適解ではなくて局所解に収束することがある
- 学習率が高すぎると学習が収束せずに発散することがある
数式は難しく見えるかもしれませんが,よく考えればそんなに難しくはないのと,数式を覚える必要はなく,最急降下法がどんなアルゴリズムなのかを理解し,数式をみたら「あ〜当然こうなるよね」と思えればOKです!
実際の業務では最急降下法をスクラッチで実装することはなく,ほとんどの場合は既にあるライブラリを使って実装することになります.
それでもアルゴリズムの背景をきちんと理解していれば,学習の過程や結果をみて正しいアクションを取ることでより良いモデルを作れるようになるでしょう!
次回の記事では解析的に最適解を求める方法を紹介します.通常の機械学習のアルゴリズムでは最急降下法を使って求めるのが一般的ですが,線形回帰ではこれを解析的に求めることができます.(つまり,数式を変形していって求めることができるわけです.)
次回の内容も,一般的に知られている有名な内容なのでしっかり学習していきましょう!
それでは!
追記) 次回の記事を書きました. 線形回帰は正規方程式を使って求めるの方がより一般的なので,超重要記事です.



















[…] – AI研究所 株式会社VOST 2024/1/14閲覧 最急降下法を図と数式で理解する(超重要)【機械学習入門3】 米国データサイエンティストのブログ 2024/1/14閲覧 Learning rate, Wikipedia […]