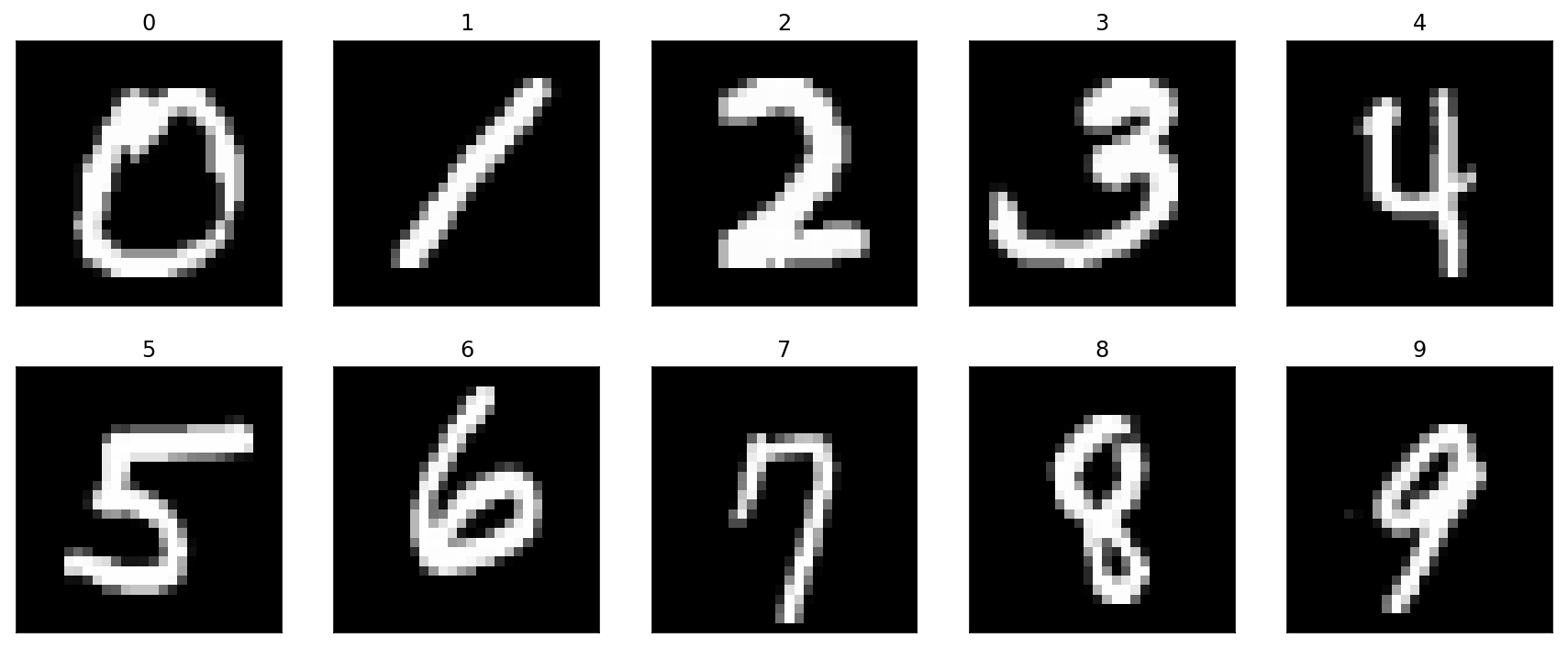データサイエンス入門の機械学習編第25回です.(講座全体の説明と目次はこちら)
追記)機械学習超入門動画講座を公開しました!動画で効率よく学習をしたい人はこちら(現在割引クーポン配布中です)
今回の記事は,前回の記事に引き続きPCA(主成分分析)についてやっていきます.
今回は,PCAを使って次元削減したあとに実際にモデルを学習してみます.次元を削減したことで学習コストが下がったり,精度がどう変わるのかをみてみましょう!
前回の記事で扱ったirisデータセットのような特徴量が4つしかないようなデータセットではあまり違いがわからないので,今回は画像の分類をしてみたいと思います.画像がピクセルの数だけ特徴量になるので,PCAを行って低次元にすることでかなりのメリットが感じられます.
目次
MNISTデータセット
今回扱うのは,かの有名なMNISTデータセットです.
MNISTデータセットは,0から9の手書き文字のデータセットで,以下のような画像が用意されています.
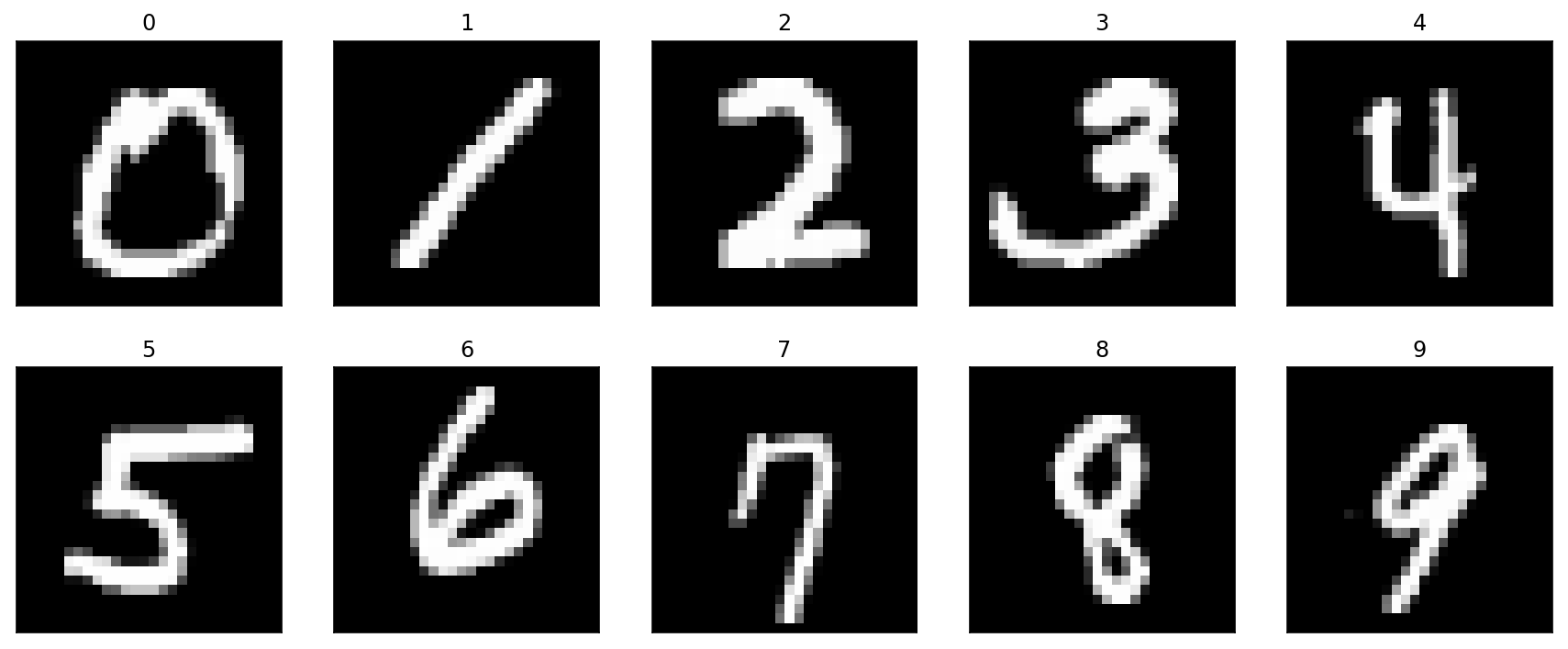
機械学習のモデルを使って,これらの画像を0〜9のクラスに分類していきます.
例えば葉書の郵便番号を自動で認識するようなアルゴリズムに応用できそうですね!

と思うかもしれませんが,例えば28×28のピクセルの画像の場合,28×28=784個のピクセル値を784個の特徴量として扱えばOKです.
実際にデータセットを見てみるとわかりやすいです.
データ取得
MNISTデータセットはあまりにも有名なデータセットなので,色々なところから取得できますが,今回はテーブルデータとして扱うのに最適な形で取得できる sklearn.datasets.fetch_openml を使って以下のようにデータを取得します.
|
1 2 3 |
from sklearn.datasets import fetch_openml # DLに少し時間がかかります. mnist = fetch_openml('mnist_784') |
実行するとデータを取ってきますが,場合によっては10分以上かかるかもしれません.
データ確認
データが取得できたら, .data でデータにアクセスすることができます.DataFrameの形で保存されています.
|
1 |
mnist.data.head() |

このように,それぞれのピクセルがpixel1〜pixel784のように,784個の特徴量として扱える形になっています.今見えてる値は全部0ですが,これは各ピクセルの値です.
.describe() で統計値を見てみましょう.
|
1 |
mnist.data.describe() |

データは全部で7000個あり,ピクセル値は大体0〜254あたりであることがわかります.
通常ピクセルの値は8bit(0~255)で表され,0が真っ黒で,値が増えるほど白くなり,255で真っ白になります.光の量だと思うと覚えやすいです.
Pythonで画像を扱う際に必要な知識は全て「データサイエンスのためのPython動画講座」で学習することができるので,今後画像を扱うデータサイエンスをやりたい人は是非チェックしてみてください.☆4.8の超高評価いただいております!
pixel1~10や,pixel781~784は画像の端っこになるので,どの画像でも黒(0)で最小値も最大値も0になってます.
また,それぞれのデータの正解ラベルは .target でアクセスできます.
|
1 |
mnist.target |

それでは,実際にどういう画像なのか見てみましょう.以下のように.reshape()を使って先ほどのDataFrameの形から2次元データの画像形式に戻してあげましょう
|
1 2 3 4 5 |
# 画像を再構成 import matplotlib.pyplot as plt idx = 0 im = mnist.data.loc[idx].values.reshape(28, 28) plt.imshow(im, 'gray') |
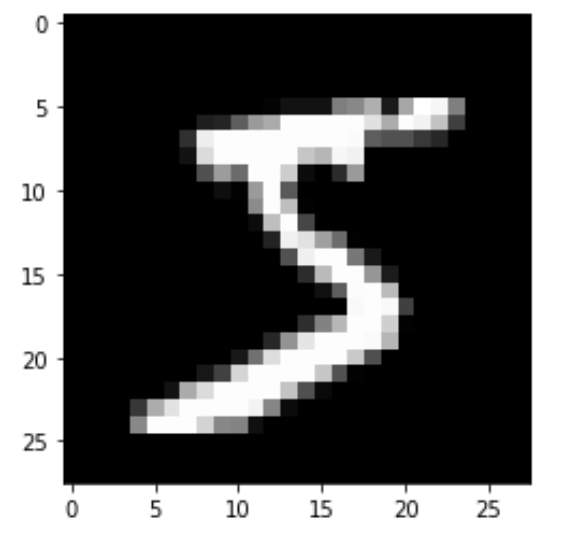
このように,多くのピクセルが黒(0)なのがわかります.
学習データとテストデータ作成
今回もhold-outで学習データとテストデータを7:3で分割します.
|
1 2 |
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(mnist.data, mnist.target, test_size=0.3, random_state=0) |
標準化
PCAを実行する前に標準化が必要なので,StandardScalerを使って標準化をします.
|
1 2 3 4 5 6 |
# 標準化 from sklearn.preprocessing import StandardScaler scaler = StandardScaler() scaler.fit(X_train) X_train = scaler.transform(X_train) X_test = scaler.transform(X_test) |
この時,テストデータである X_test も, X_train で .fit した scaler で .transform して標準化することに注意しましょう
PCA
それでは,前回の記事を参考にPCAを実施してみましょう.今回は主成分の数を指定するのではなくて,累積寄与率を指定して95%になるまでの主成分を返すようにします.
|
1 2 3 4 5 6 7 |
# PCA from sklearn.decomposition import PCA pca = PCA(n_components=0.95) pca.fit(X_train) X_train_pc = pca.transform(X_train) X_test_pc = pca.transform(X_test) print(f'{X_train.shape[-1]} dimention is reduced to {X_train_pc.shape[-1]} dimention by PCA') |
|
1 |
784 dimention is reduced to 323 dimention by PCA |
PCAをした結果,784次元を323次元に削減することができました!(5%の情報が減っていることに注意しましょう)
ロジスティック回帰でモデル構築
PCAができたら,PCA後のデータ( X_train_pc )でモデル構築をします.この時,どのくらい時間がかかったか測っておきます.
|
1 2 3 4 5 6 7 8 |
# ロジスティック回帰 from sklearn.linear_model import LogisticRegression import time model_pca = LogisticRegression() before = time.time() model_pca.fit(X_train_pc, y_train) after = time.time() print(f'fit took {after-before:.2f}s') |
|
1 |
fit took 4.88s |
すると,大体5秒くらいでモデル学習ができました.やはりPCAしたとはいえ323個の特徴量で49000個のデータを学習するには時間がかかります.
予測
試しに一つ予測してみましょう.
|
1 |
model_pca.predict(X_test_pc[0].reshape(1, -1)) |
|
1 |
array(['0'], dtype=object) |
正解ラベルを見てみると
|
1 |
y_test.iloc[0] |
|
1 |
'0' |
正解しているのがわかります.
PCAなしでロジスティック回帰
PCAなしバージョンでもロジスティック回帰をしてみましょう.コードは上のものとほとんど同じですね.学習データに使うのはPCA前の X_train であることに注意してください.
|
1 2 3 4 5 6 7 8 |
# PCAなしでロジスティック回帰 from sklearn.linear_model import LogisticRegression import time model = LogisticRegression() before = time.time() model.fit(X_train, y_train) after = time.time() print(f'fit took {after-before:.2f}s') |
|
1 |
fit took 11.02s |
当然ですが,PCAをする前のデータは次元数が多いため,学習にも時間がかかっているのがわかります.
では,これらのモデルを評価してみましょう.今回は練習も兼ねて第23回で紹介した多クラス分類のROCとAUCを使ってみましょう!
AUCでそれぞれのモデルを評価する
AUCの計算はPCAのモデルと普通のモデルに対して計2回行うので,こういうのは関数にしてしまいましょう!
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
# ROC import numpy as np from sklearn.metrics import roc_auc_score from sklearn.metrics import roc_curve, auc from sklearn.preprocessing import label_binarize def all_roc(model, X_test, y_test): # クラス数 n_classes = len(model.classes_) # OvRのためone-hotエンコーディング y_test_one_hot = label_binarize(y_test, classes=list(map(str, range(n_classes)))) predict_proba = model.predict_proba(X_test) fpr = {} tpr = {} roc_auc = {} # 各クラス毎にROCとAUCを計算 for i in range(n_classes): fpr[i], tpr[i], _ = roc_curve(y_test_one_hot[:, i], predict_proba[:, i]) roc_auc[i] = auc(fpr[i], tpr[i]) # micro平均 fpr['micro'], tpr['micro'], _ = roc_curve(y_test_one_hot.ravel(), predict_proba.ravel()) roc_auc['micro'] = auc(fpr['micro'], tpr['micro']) # macro平均 all_fpr = np.unique(np.concatenate([fpr[i] for i in range(n_classes)])) mean_tpr = np.zeros_like(all_fpr) for i in range(n_classes): mean_tpr += np.interp(all_fpr, fpr[i], tpr[i]) mean_tpr = mean_tpr / n_classes fpr["macro"] = all_fpr tpr["macro"] = mean_tpr roc_auc["macro"] = auc(fpr["macro"], tpr["macro"]) return fpr, tpr, roc_auc |
コードの詳細は第23回を参照してください.
そしてこの関数を使って,それぞれのモデルの評価指標を計算します.
|
1 2 |
fpr, tpr, roc_auc = all_roc(model, X_test, y_test) fpr_pca, tpr_pca, roc_auc_pca = all_roc(model_pca, X_test_pc, y_test) |
扱いやすいようにDataFrameにします.
|
1 2 3 |
import pandas as pd result_df = pd.DataFrame([roc_auc, roc_auc_pca]).T.rename(columns={0:'normal', 1:'pca'}) result_df |
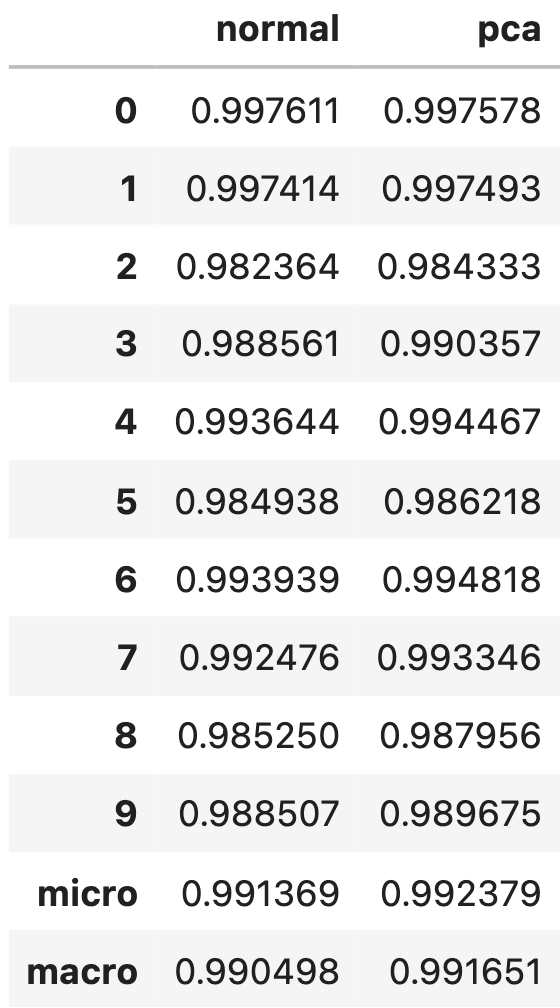
全体的にPCA後の方が少しだけAUCが高くなっているのがわかります.
差分をとってみるとこんな感じ
|
1 2 |
result_df['pca - normal'] = result_df['pca'] - result_df['normal'] result_df |
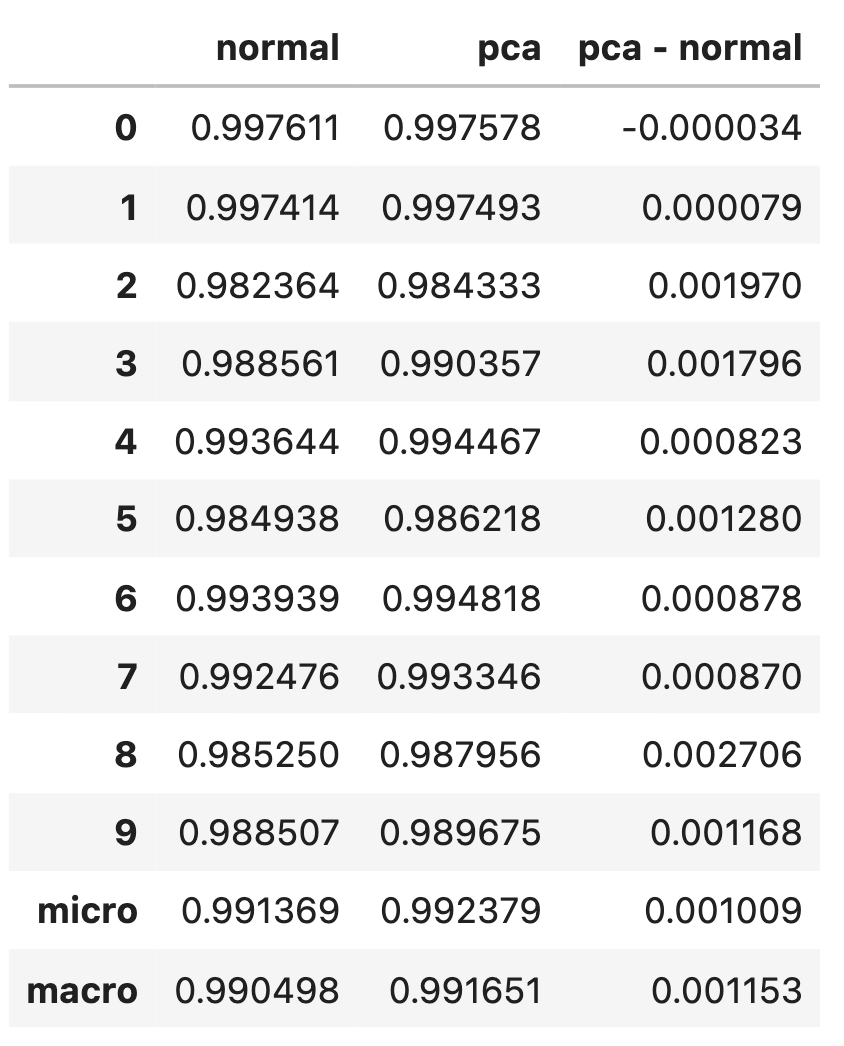
ほとんどのクラスでAUCが上がっているところを見ると,PCAをした方が本当に微小だけど精度が上がったといってもよさそうです.
実際にはkfoldのクラスバリデーションなどするとちゃんと汎化性能をみれるのですが,今回は割愛します.
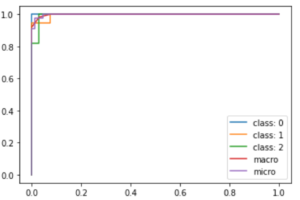
興味がある人はそれぞれのROCをplotしてみてもいいでしょう!(どれも同じようなカーブになるのでみにくいですが,,,)
とにかく,今回言えることは「PCAで次元削減したからといって,精度を落とすことなく学習スピード向上が期待できる」ということです.
PCA後の方が精度が高い?

これは結論からいうと「精度向上は多くの場合で期待できるが,それを目的でPCAをやるのは少し違う」って感じでしょうか.
そもそもなぜPCAを行うと精度向上が見込めるかというと,特徴量が多いことによる過学習(Overfitting)を避けることができ,結果汎化性能が上がるからです.
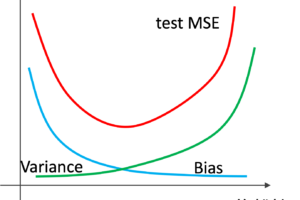
これは第12回のBias-Variance Tradeoffに関係しています.特徴量が多いということは,モデルがそれだけ複雑になりHigh Varianceとなります.
PCAをすることで次元を削減できるので,Varianceを下げることができ精度向上が期待できるのです.(もちろん,データにもよりますが!)

ダメじゃないんですが,一般的にLassoのような正則化項を使って特徴量選択をした方がPCAより精度が高くなります.なので,精度をあげたいならPCAではなくてLassoを使いましょう.
また,PCAを「特徴量選択」のように使う人も時々いますが,特徴選択をするなら普通に正則化項を使うのがいいです.PCAはあくまでも「低次元への変換」であり,その変換には全ての特徴量を使ってることに注意しましょう.
なので,PCAをアルゴリズムに組み込む場合は,予測する未知のデータも全ての特徴量が必要です.「不要な特徴量を取得する手間を減らせる」というメリットはないので注意です!
まとめ
今回はPCA後の主成分を特徴量としてモデル構築することによって,学習スピードや精度がどう変わるのかをMNISTデータセットを使ってみてみました.
- PCAをすることで次元が減り,学習スピードの大幅な改善を期待できる
- 次元を減らすことで,過学習を避け精度向上が期待できる
- 過学習を避けるための精度向上が目的であれば,PCAよりもLassoの方が適している
- 特徴量選択をしたければ,PCAよりもLassoの方が適している
また,PCA後に回帰モデルを学習することをPCR(Principal Component Regression)というので,これも頭の片隅に入れておきましょう.今回は分類タスクを例にとりましたが,回帰も同じです.
今回はPythonのコードが多くなってしまいましたが,Pythonのコーディングに自信がない人は是非動画講座や,僕の運営しているコミュニティで練習してください!
それでは!
追記) 次回の記事書きました!次回から教師なし学習である「クラスタリング」のアルゴリズムについて解説します!