XGBoostの概要とPython実装をわかりやすく解説【機械学習入門32】

機械学習入門講座も第32回になりました．(講座全体の説明と目次はこちら)

追記) 機械学習超入門本番編ではXGBoostについてさらに詳しく解説をしています．勾配ブースティング決定木アルゴリズムのスクラッチ実装もするので，さらに理解を深めたい方は是非受講ください:)

今回はアンサンブル学習の一つである，XGBoostというアルゴリズムを紹介します．

XGBoostはKaggle等のコンペでも上位ランクの常連になっているアルゴリズムで，とても精度が高い強力なモデルを作ることができます．(こちらにXGBoostを使った上位ランクのリストがありますが，これでもまだ一部だと思うのですごいですね^^;)

一部理論面で理解が難しいところもあるXGBoostですが，かなりわかりやすく解説していくので，是非ついてきてください！コンペなどではよく使うアルゴリズムかと思いますが，是非理論と長所/短所を理解した上で使えるようになりましょう◎

※XGBoostの理論の数式展開は結構骨が折れるので，本講座はあくあまでも入門講座ということで本記事では理論の概要とPythonでの実装にとどめます．興味がある人は原論文を読んでみてください！

XGBoostとは？

XGBoostは，eXtreme Gradient Boostingの略で，決定木の勾配ブースティングアルゴリズムです．

・・・は？

って感じですよね．大丈夫です．全部わかるように説明します！

まずは，「決定木」「勾配」「ブースティング」の３つのキーワードに注目しましょう．

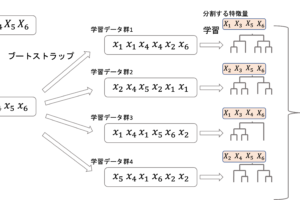
XGBoostはブースティングアルゴリズムをベースとします．ブースティングについては第30回で紹介した通りですが，モデルがうまく予測できなかったデータに重みをつけてまたモデルを学習させて・・・というのを繰り返して最後にそれぞれのモデルを使って最終的な予測をするアルゴリズムでしたね

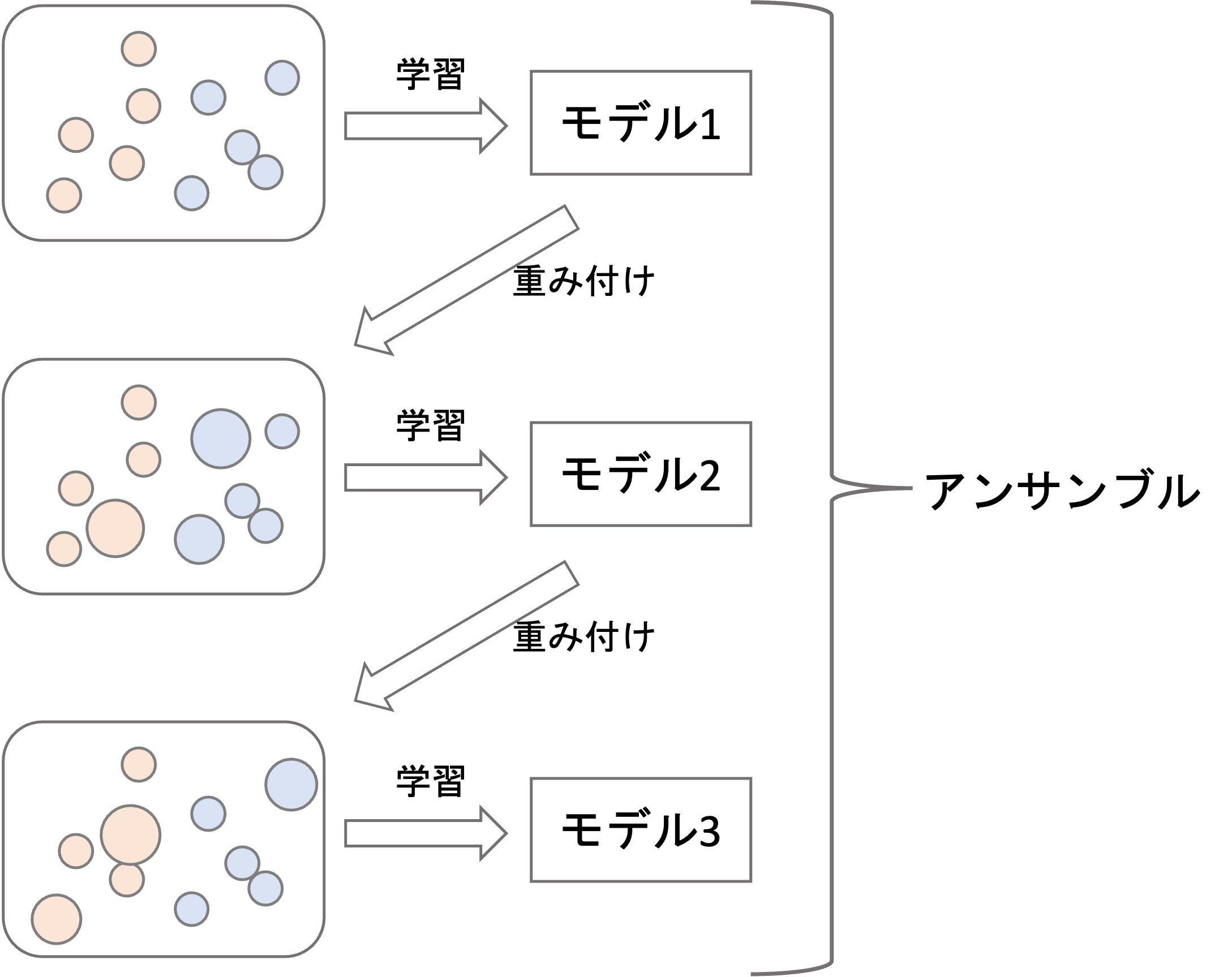
「勾配」は，第3回で触れたように，残差が少しでも小さくする方向のことで，XGBoostは残差を徐々に小さくするように学習を進めていきます．

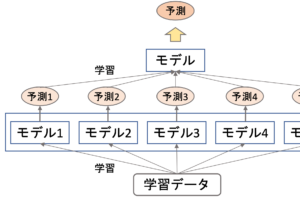
なので，例えば上図のようにモデル1, モデル2, …とブースティングで直列にモデルを学習させるときに，モデル1→モデル2, モデル2→モデル3, …と残差が小さくなるように学習をしていきます．なので，普通のブースティングのように学習データの重づけをするのではなく，残差を計算して，それが小さくなるように次の決定木を学習することになります．

イメージとしては下図のようになります．

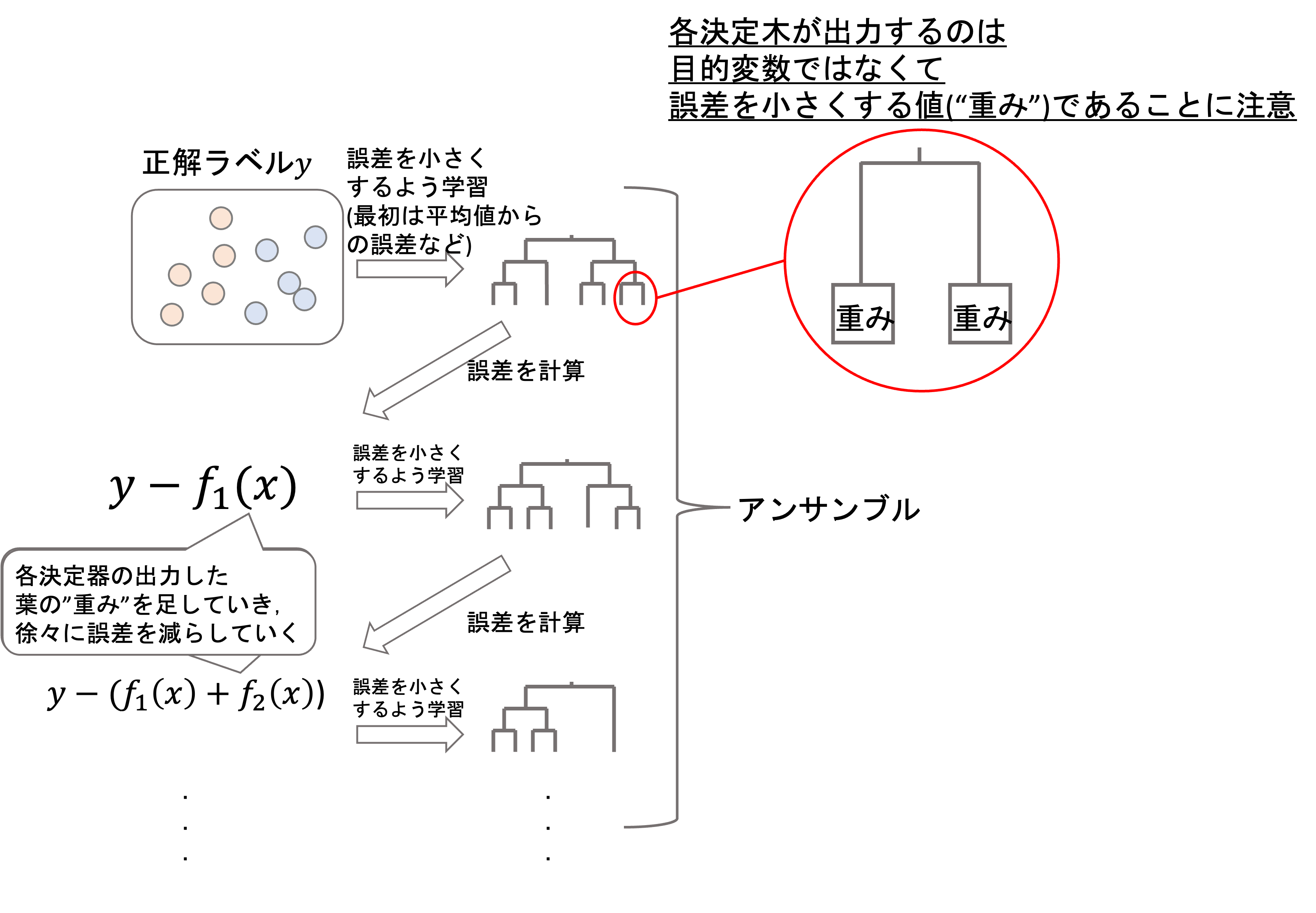
各決定木は，目的変数の値を出力するのではなく，ある値(これを葉の”重み”と呼びます)を出力するようにし，それを足し合わせて徐々に残差が減っていくようにするのです．(上図では，\(t\)時点での決定木の出力結果を\(f_t(x)\))としています．ただし\(x\)は学習データです．

つまり，最初のイテレーションでは一つ目の決定木の出力結果との残差\(y-f_1(x)\)を計算し，次のイテレーションではその残差を減らすための”重み”を学習します．(通常，最初の決定木の出力結果は平均値や，適当な値だと思っていただければいいです．つまりこの段階では残差はある程度大きいと思ってください)

二回目の決定木の学習で，残差を小さくするための値(=重み)を学習していきます．そして，次のイテレーションでは\(y-(f_1(x)+f_2(x))\)を残差としてそれをまた小さくするための重みを次の決定木で学習していきます．

これを繰り返すことで残差を減らしていき，XGBoostでは最終的な予測の結果を\(\sum^{K}_{k=1}f_k(x)\)とします．(実際には各決定木にある係数をかけます．これについては後述します．)

このようにが勾配(残差が小さくなる方向に)に沿ってモデルが学習されていくことから”Gradient”の名前がついています．

またこのように，XGBoostはモデルに決定木を使います．ランダムフォレストも，「バギング+決定木」で，モデルに決定木を使ってましたね．これはやはり，決定木はhigh varianceのモデルなのでアンサンブルによって効果がでやすいという点があります．

XGBoostのアルゴリズム概要

XGBoostは以下の損失関数を小さくすることを目的として学習を進めていきます．

げ，また難しそうな数式がっ・・・

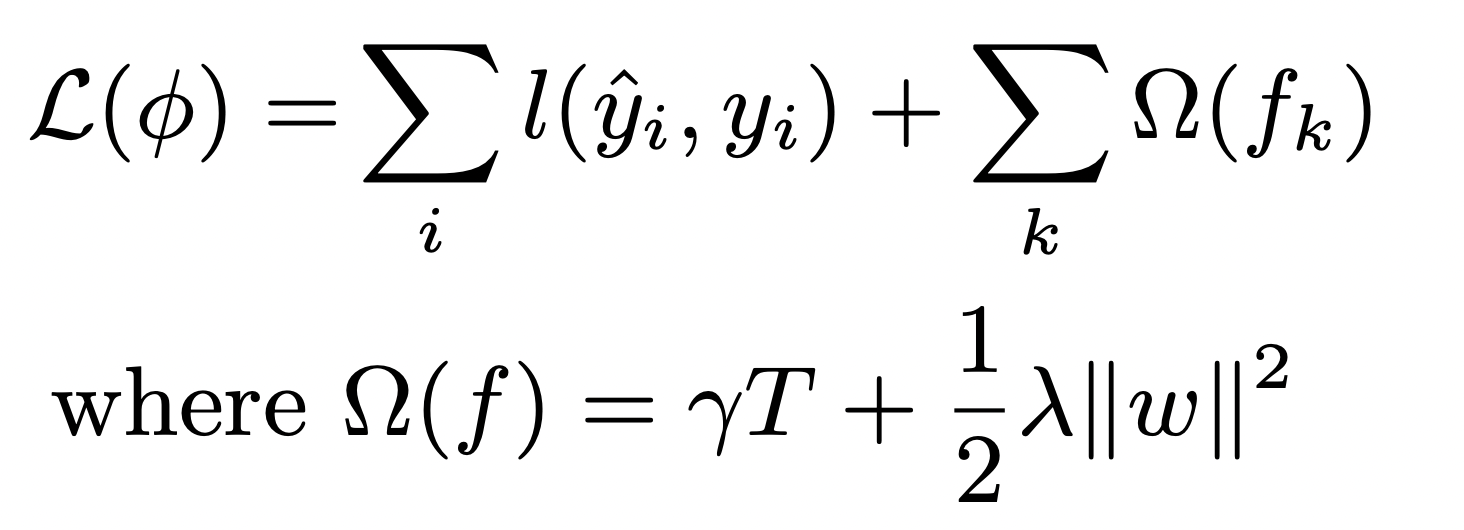
実はそんなに難しくないので，丁寧に解説するので頑張って理解しましょう！

まず，\(l(\hat{y}_i, y_i)\)は予測値\(\hat{y}_i\)と正解値\(y_i\)の残差です．それを\(\sum^{}_{i}\)し，全てのデータの残差の総和を取ります．

そして\(\sum_{k}\Omega(f_k)\)は正則化項の役割をします．正則化項については第14回で解説してます．要はペナルティを与える項ですね

どんなペナルティを与えるかというと，\(\gamma T+\frac{1}{2}\lambda||\omega||^2\)というものです．

\(T\)は決定木の葉の数，\(\omega\)はその木の最終的に予測にした葉のスコア(つまりは決定木でいう予測値です．XGBoostでは重みと言います)です．

\(\gamma\)とか\(\frac{1}{2}\lambda\)とかの細かい係数は今回は気にしないでください．ただのハイパーパラメータです．

これを\(\sum_{k}\)し，アンサンブルに使った全ての木の総和をとっています．

つまりは，XGBoostでは葉の数と各木の最終的な葉の重みにペナルティをかけ，木が複雑になり過ぎないようにしています．これはもちろん，過学習を避けるためですね！先のXGBoostの概要図において，最初のイテレーションでいきなり残差を埋めるための\(f(x)\)が大きかったら，残差がなくなってしまいイテレーションが早く終わってしまってモデル数も少なくなりアンサンブルとしての価値が無くなりますし，そんなすぐに残差がなくなったら，それは明らかに過学習してるといえるでしょう．

さて，先ほどの式にブースティングの要素を入れてみます．ブースティングは一つ前のモデルの結果を使って新たなモデルを学習することを繰り返すんでした．そして，XGBoostでは以前学習したモデルの結果を足し合わせて予測を出します．

つまり，\(i\)番目のデータのある時点\(t\)でのモデル(XGBoost)の予測結果\(\hat{y}^t_i\)は前の(モデル全体の)予測\(\hat{y}^{(t-1)}_i\)とその時点での決定木の予測値\(f_t(x_i)\)の足し算になります．(実際にはこれに係数をつけていきますが，それについてはまた後述します)

つまり先ほどの式は以下のような漸化式で記述することができるわけです．

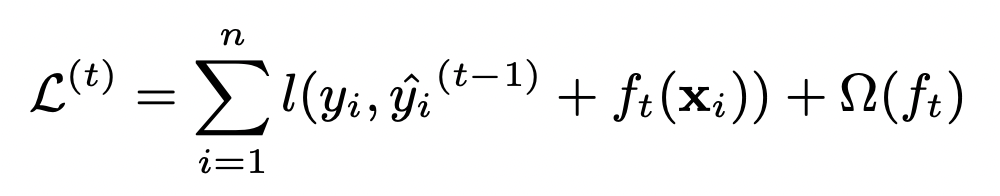
この式は\(t\)時点での損失の式であることに注意しましょう．なので，正則化項の\(\sum_{k}\)も外れ，その時点での決定木のものになってます

そしてこの損失が最小になる\(f_t()\)と葉の重み\(\omega\)を求めることになります．この求め方については数式の導出が長く，本講座で扱う範疇を超えるので割愛します．興味がある人は原論文を読んでみてください．

過学習を抑えるための工夫

XGBoostは，先ほどの正則化項以外にも色々と過学習を抑えるための工夫をしています

Shrinkage(縮小)

それぞれの決定木の結果に係数\(\eta\)(０〜1)をつけることで，それぞれの決定木の影響を小さく(縮小=shrinkage)します．

ある時点\(t\)でのXGBoostの全体の予測値\(\hat{y}^t_i\)はそれ時点より一つ前(つまり一つ前のイテレーション)の予測値\(\hat{y}^{(t-1)}_i\)にその時点で学習した決定木の結果\(f_t(x_i)\)を足したもの，つまり

$$\hat{y}^t_i=\hat{y}^{(t-1)}_i+f_t(x_i)$$

でした．XGBoostでは残差を学習していくので，毎回の決定木\(f_t(x_i)\)は，その残差を小さくするためのものです．が，これをそのまま付け加えてしまうと，簡単に過学習してしまいます．(決定木が出力する値は，正解値との残差を埋める値です．そのまま採用してしまうと一気に残差がなくなってしまう恐れがあります．そうするとそこで学習は終わり，使用するモデル数も少なく過学習してしまうのです)

そのため，\(0<\eta<1\)の係数を掛け，毎回の決定木の結果を縮小(shrinkage)させます．イメージとしては学習率(learning rate)に近い役割をします．つまり値が小さいとそれだけ残差のギャップを埋めるのに時間がかかり，学習が長引きます．

$$\hat{y}^t_i=\hat{y}^{(t-1)}_i+\eta f_t(x_i)$$

つまり，XGBoostの最終的な予測値は，全ての決定木の予測結果の総和ではなく，係数\(\eta\)をつけた総和になります．

$$\hat{y}_i=\sum^{K}_{k=1}\eta f_k(x_i)$$

ただし\(K\)はアンサンブルする決定木の数(=イテレーションの回数)です．

\(\eta\)は小さければ小さい方がいいとも言われていますが，現実的な数字は0.3以下で，特に0.1以下がいいとされている印象です．が，これはお使いのマシンスペックに合わせて決めていただければ良いかと思います．

Column Subsampling

これは前回の記事で解説したランダムフォレストで紹介したものと同じです．

一つ一つの決定木の分割に使う特徴量をランダムに選択します．(つまり，一部の特徴量のみ分割して決定木を作ります)

詳細は前回の記事に書いているので割愛しますが，XGBoostもランダムフォレスト同様にこの手法を採用し，過学習を防いでいます．

他にも，決定木の分割の近似アルゴリズムなどが原論文にありますが，本記事では割愛します．なお，本記事の数式はこちらの論文を参考にしております．

PythonでXGBoostを使う

それでは，いつも通りPythonでXGBootを使うやり方を簡単に紹介します．

XGBoostをPythonで扱うには，まずXGBoostのパッケージをインストールする必要があります．(scikit-learnの中には実装されていないので注意してください．)

Terminalで pip install xgboost でインストールできます．Jupyterのセルで実行する場合は %pip install xgboost のように % をつけて実行すればOKです．

インストールができたら以下のように xgboost をimportします．色々とAPIが用意されていますが，scikit-learnと同じインタフェースが用意されているので，本記事ではそれを使います．

回帰モデルには xgboost.XGBRegressor を，分類モデルには xgboost.XGBClassifier を使います．どちらも仕様はほとんど同じです

今回は前回まで使っていたタイタニックのデータセットを使って，搭乗者が生存するかどうかの2値分類をする分類モデルを作ってみましょう．(タイタニックデータについてはデータサイエンスのためのPython第11回を参照ください)

データ準備

これはXGBoostの特徴の一つです．詳細のアルゴリズムは原論文の3.4 Sparsity-aware Split Findingを参照ください．簡単にいうと，最初に欠損値がないデータが綺麗に分かれるように決定木の分割を行い，その後に欠損値データを右にするのか左にするのかをみて，スコア(例えばジニ不純度等)が最も良くなるように分割をします．

これを各ノードで試してくれるので，特徴量によって分割位置が異なり，これが欠損値代入と同じような処理をしてくれています．(以上の説明がわからなくてもあまり気にしなくてOK.アルゴリズムの詳細は本講座の範疇を超えているので．)

今回は，このデータセットを学習データとテストデータを7:3に分けます．

学習

それでは学習データに対してXGBoostを学習させてみます．

基本的な使い方は他のscikit-learnの機械学習モデルのクラスと同じで， model=XGBClassifier() でインスタンスを生成して， model.fit(X_train, y_train) で学習をさせればOKです．

が，色々とパラメータをセットできるので，簡単によく使うものだけピックアップして解説します．

• n_estimators : ブースティングの回数(=学習する決定木の数)．デフォルトは100．
• learning_rate : shrinkageの\(\eta\)．デフォルトは0.3なので少し高め．(低スペックマシンでの実行を想定しているのだと思われます．)
• max_depth : 決定木の最高の深さ．デフォルトは6
• eval_metric : ブースティング時の各イテレーション時に使う評価指標(特に後述するearly stoppingに使用). sklearn.metricsのメソッドを渡すか，自作してもOK．デフォルトは 'logloss'
• early_stopping_rounds : early stoppingする際の，最低限ブースティングのイテレーションをする回数

他にも色々とありますが，まずはこのあたりのパラメータを押さえておけばOKです．

early stoppingというのは，ブースティングのイテレーション時に評価指標がこれ以上下がらなくなったら自動で学習をやめてくれます．この仕組みにより， n_estimators や learning_rate のパラメータを探索する必要がほとんどなくなります． n_estimators には高い数字を， learning_rate には低い数字をセットしておけば，あとはearly stoppingで学習を回せば最も精度が高くなったところで自動で学習をやめてくれます．

今回は以下のように設定し，early stoppingするようにしておきましょう．

.fit()のよく使う引数は以下です．

• eval_set : (X, y)のリストで，これを渡すと，ブースティング時の各イテレーションごとにこのデータセットを使って評価してくれる．
• verbose : Trueにすると，各イテレーションでの評価指標などを表示し，イテレーションの軌跡を確認できる．

今回は，テストデータを各イテレーションで評価するデータとして使います．

すると，このように各イテレーションでの評価指標を表示してくれます．

今回の場合は，[5]の時に最もloglossが低くなっており，そこからearly_stopping_rounds(=10回)以下にならなかったので，16回のイテレーションで終わっています．

これらは model.best_score と model.best_iteration で確認することができます．

また， .fit() はxgboostのモデルを返すので，そこも注意しておきましょう．( model 変数に格納しなくても， model 変数はすでに学習済みになっています．)

予測

他のsklearnの機械学習クラスと同様， .predict() や .predict_proba() で予測することができます． sklearn.metrics.log_loss で評価指標を計算して，イテレーション時の最小のloglossと一致することを確認しましょう．

興味がある人は他の指標もみてみてください！

特徴量の重要度

ランダムフォレスト同様，XGBoostも特徴量の重要度を出すことができます．( xgboost.plot_importance(model) でも同様なplotをしてくれる便利な関数が実装されています．)

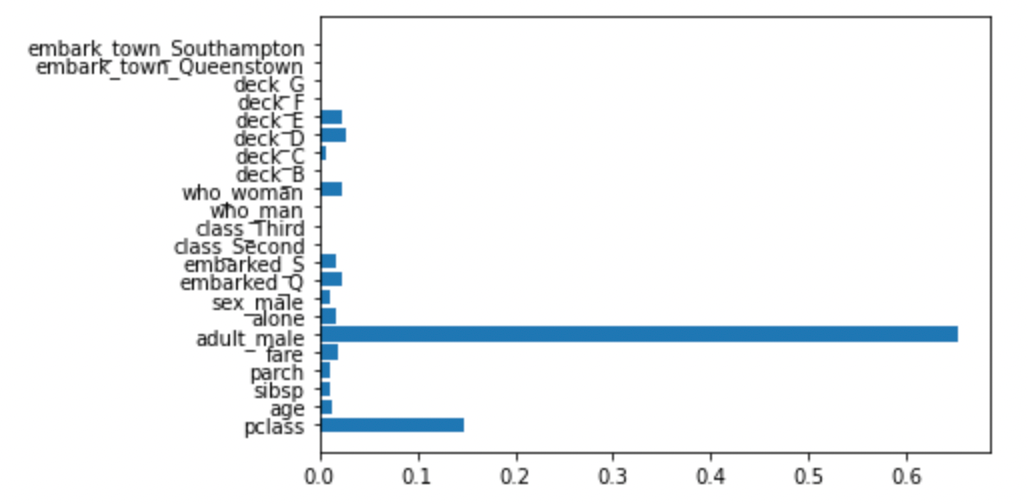
前回の記事でランダムフォレストとは結構異なっているのがわかります．

今回もかなり長くなってしまったのでこのあたりでまとめます・・・ここまで読まれた方，お疲れ様ですmm

まとめ

今回はXGBoostというアルゴリズムを紹介しました!

• XGBoostは非常に精度が高い強力な機械学習アルゴリズムである
• XGBoostは決定木の勾配ブースティングアルゴリズムである
• XGBoostは，ブースティング時に誤差が徐々に小さくなるように決定木を学習していく
• 正則化項やshrinkage，column subsampling，early stoppingなどを行い，過学習を避けている
• XGBoostは欠損値の対処をアルゴリズムに組み込んでいるので，欠損値はそのまま学習アルゴリズムに使うことができる．

XGBoostは，比較的新しいアルゴリズムで，登場以降多くのコンペの上位モデルで採用されてきました．

また，このXGBoostが世に出てからまもなく，また新たな「決定木の勾配ブースティングアルゴリズム」がでています．XGBoostを超える(!?)アルゴリズムとしてここ数年注目されているのがLightGBMと呼ばれるアルゴリズムです．

両者は似てるのですが，異なるアルゴリズムです．XGBoostがある程度わかれば，LightGBMも簡単に理解できるでしょう！

次回はそんなLightGBMについて解説をしていきます．さらに強力なアルゴリズムとも言えるので，是非このまま学習を進めていきましょう！

それでは！

追記) 次回の記事書きました！

LightGBMを超わかりやすく解説(理論+実装)【機械学習入門33】