データサイエンス入門の機械学習編第15回です.(講座全体の説明と目次はこちら)
追記)機械学習超入門動画講座を公開しました!動画で効率よく学習をしたい人はこちら(現在割引クーポン配布中です)
今回はkNNというアルゴリズムを紹介します.kNNは分類でよく使うアルゴルリズムですが,回帰にも使えるので,今回はパラメトリック手法である線形回帰と比較する形でノンパラメトリック手法であるkNN回帰について紹介していきます.
「線形回帰もまだ理解しきれてないのに新しいアルゴリズムなんて...」と思うかもしれませんが,そんなに難しいアルゴリズムではないのでサクッと学習してしまいましょう!
目次
kNNとは?
kNNは,k Nearest Neighborといわれる機械学習アルゴリズムで,日本語ではk最近傍法と呼ばれます.日本でも「kNN」というのでこの略称で覚えておきましょう!
kNNはよく分類のアルゴリズムで使われることが多いんですが,回帰問題にも使うことができます.(区別するために本講座ではkNN回帰とします.)
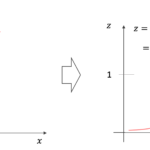
kNN回帰がどういうアルゴリズムかというと,まずは以下の図をみてください
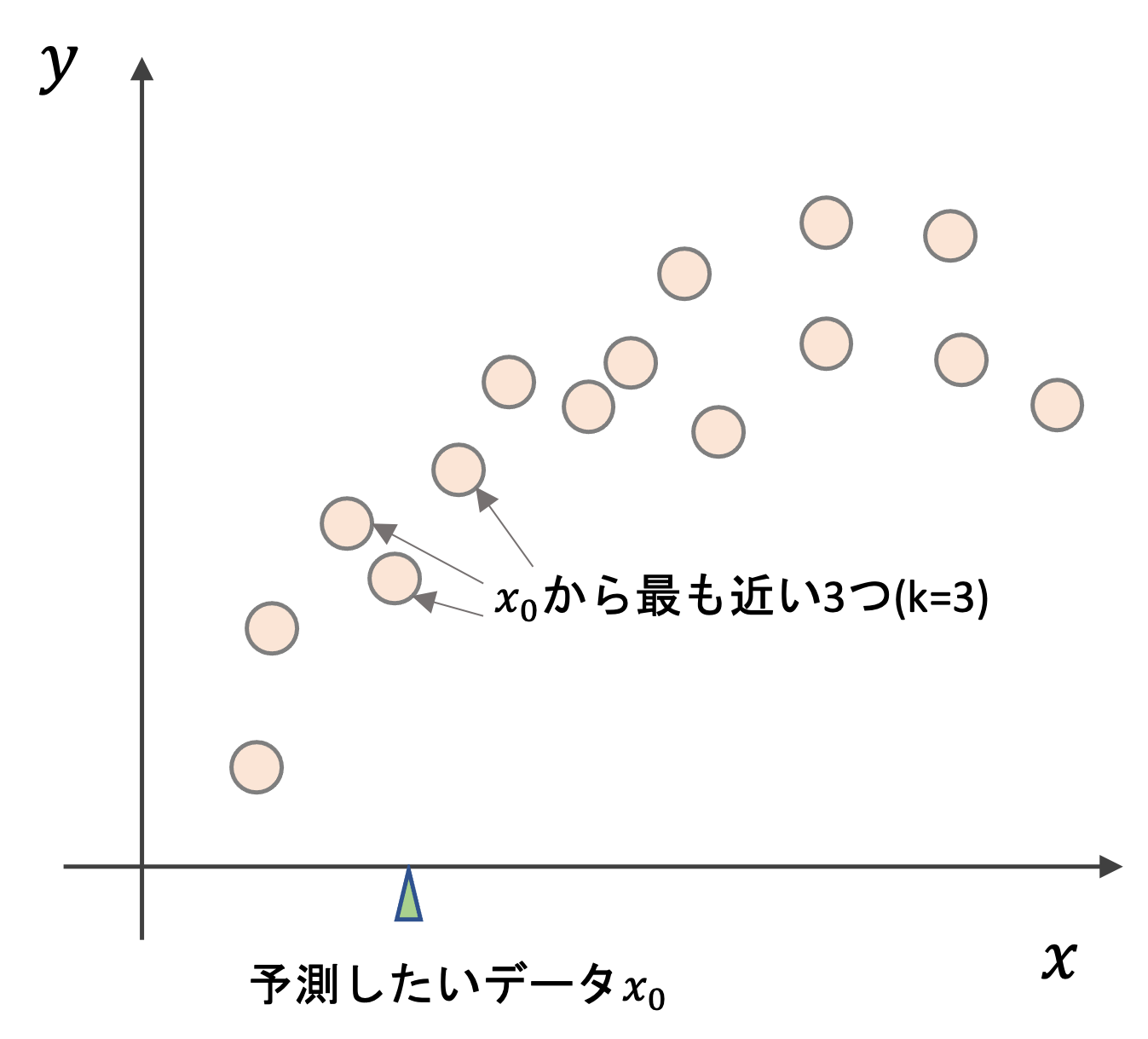
学習データが上記のようにあったとします.あるデータ\(x_0\)を予測する際に,kNN回帰では,そのデータの近くのk個の学習データを見て,それらの学習データの平均値を\(x_0\)の予測値とします.
例えばk=3の場合,\(x_0\)から近い3つの学習データの\(y\)の平均を予測値とします.
式で書くと以下のような感じです.
$$\hat{f}(x_0)=\frac{1}{k}\sum_{x_i\in N_0}y_i$$
\(\hat{f}\)は本来求めたい真の回帰の式\(f\)の推定です.\(x_i\in N_0\)は\(x_0\)から最も近い\(k\)個の領域\(N_0\)の中にある学習データ\(x_i\)という意味です.その学習データの値\(y_i\)の平均をとっている式であるのがわかると思います.
アルゴリズム自体はめちゃくちゃ簡単ですね!このように,線形回帰のように数式モデルに当てはめているアルゴリズムと違って,kNNは数式モデルを使いません.このようなアルゴリズムをノンパラメトリックと言います.
何を持って「近い」とするかという問題があります.これは,どのように”距離”を定義するかによりますが,特に理由がなければユークリッド距離(Euclidean distance)と呼ばれるものを使います.詳細は割愛しますが,一般的な距離の測り方と同じなのでwikipediaのページを参考にすれば理解できるかと思います.本講座では特に理由がなければユークリッド距離を使います.
scikit-learnでkNN回帰を使う
それではPythonでkNN回帰モデルを構築してみましょう.kNN回帰も他の機械学習アルゴリズム同様,scikit-learnに実装されているのでそれを使えばOKです.
今回は第11回で使ったmpgデータセットを使ってやってみましょう.第11回同様,horsepower(馬力)からmpg(mile per gallon:燃費)を予測するモデルを作ります.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
import matplotlib.pyplot as plt import seaborn as sns from sklearn.model_selection import train_test_split df = sns.load_dataset('mpg') df.dropna(inplace=True) X = df['horsepower'].values.reshape(-1, 1) y = df['mpg'].values X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.9, random_state=0) sns.scatterplot(x=X_train[:, 0], y=y_train) plt.xlabel('horsepower') plt.ylabel('mpg') |
今回はデータの数を減らして描画したかったので, test_size=0.9 でデータをsplitします.
scikit-learnでkNN回帰を使うには, sklearn.neighbors.KNeighborsRegressor クラスを使います.基本的な使い方は今までのものと同じです.
n_neighbors 引数に,\(k\)の値を入れます.今回は\(k=3\)としましょう.|
1 2 3 |
from sklearn.neighbors import KNeighborsRegressor model = KNeighborsRegressor(n_neighbors=3) model.fit(X_train, y_train) |
kNNは距離を使うアルゴリズムなので,通常は特徴量間のスケールを標準化して合わせる必要があります.が,今回の例では特徴量が一つしかないため,標準化しても結果は変わらないので省略しています
それでは結果を描画してみましょう.いつも通りx軸の値を用意して,その値を予測した結果を描画します.
|
1 2 3 4 |
x_axis = np.linspace(45, 225).reshape(-1, 1) y_pred = model.predict(x_axis) sns.scatterplot(X_train[:, 0], y_train) plt.plot(x_axis, y_pred, 'red') |
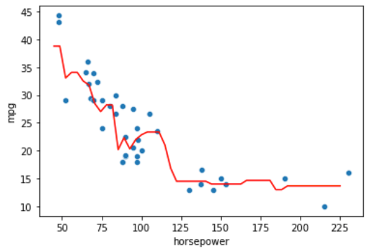
線形回帰や多項式回帰などのパラメトリックな手法と異なり,かなり柔軟なモデルになっているのがわかると思います.
kNN回帰はなにかの数式のモデルを元に学習をしているわけではないので,学習データに対して柔軟な回帰モデルを構築できます.
\(k\)を変更するとどうなるのか
試しに n_neighbors (\(k\))を色々と変えてみて結果がどう変わるかみてみましょう!
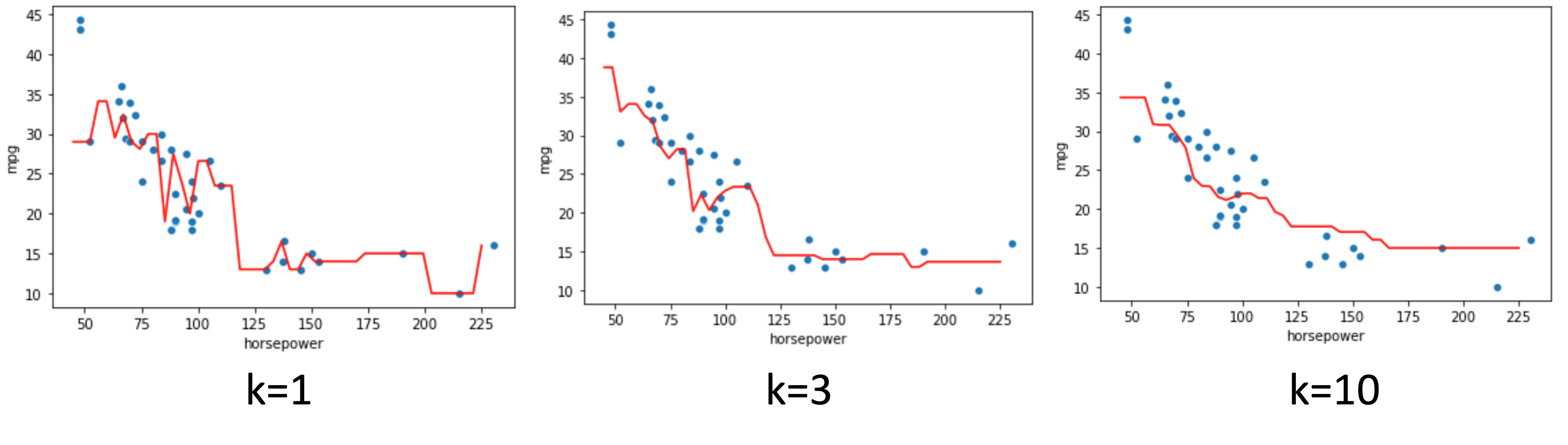
k=1の時は最も近い学習データの値をそのまま使う形になり,学習データに沿う形で回帰曲線が引かれているのがわかります.
k=3,10とkを増やすにつれ複数の学習データの平均値をとっていくので曲線は滑らかになっていきます.
つまり,kを大きくするにつれ,varianceが小さくなり,biasが上がっていくということですね!(biasとvarianceについては第12回の記事を参考にしてください!)
どの\(k\)がベストなのか?
\(k\)が大きすぎるとhigh biasになるし,小さいとhigh varianceになってしまうので適切な\(k\)を選択することが重要です.

これは,\(k\)を変えていったときのtest errorの推移をみて決めます.基本的には最もtest errorが低いものを選べばいいでしょう.
先のコードを少し変更して,いくつかの\(k\)でのtest errorを計算してplotしてみます.今回は5kCVでのcv errorをみてみましょう
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
import numpy as np import matplotlib.pyplot as plt import seaborn as sns from sklearn.neighbors import KNeighborsRegressor from sklearn.model_selection import train_test_split, KFold, cross_val_score # データ準備 df = sns.load_dataset('mpg') df.dropna(inplace=True) X = df['horsepower'].values.reshape(-1, 1) y = df['mpg'].values # k=1~10でfor loop score_list = [] k_list = np.arange(1, 30) for k in k_list: # model model = KNeighborsRegressor(n_neighbors=k) # 5kFold cv = KFold(n_splits=5, random_state=0, shuffle=True) scores = cross_val_score(model, X, y, scoring='neg_mean_squared_error', cv=cv, n_jobs=-1) # neg_mean_squared_errorは負の値なので反転させることに注意 score_list.append(-np.mean(scores)) print(f'Best performanc: k={k_list[np.argmin(score_list)]}, cv error={np.min(score_list)}') |
|
1 |
Best performanc: k=19, cv error=18.349417604637846 |
すると,今回の結果はk=19の時cv errorが最小になるようです.
cv errorの推移を見てみましょう.
|
1 2 3 |
plt.plot(k_list, score_list) plt.xlabel('k') plt.ylabel('5fold cv error') |
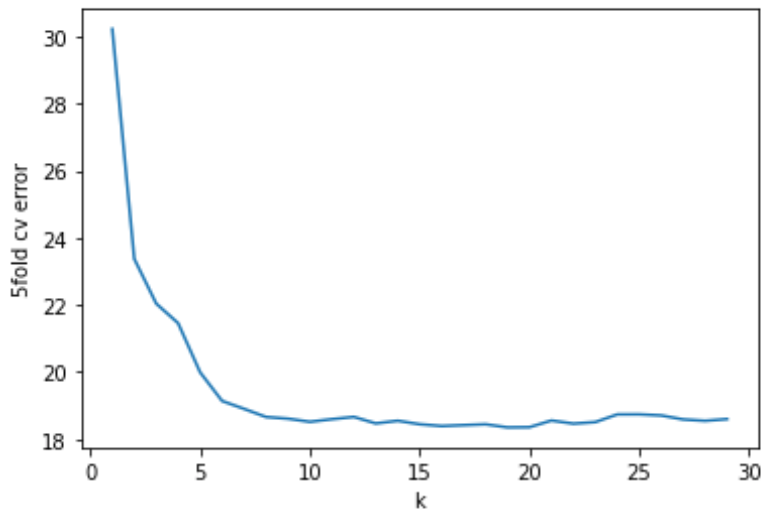
kが小さいとvarianceが大きいのでcv errorも高くなっており,kが大きくなるにつれvarianceが小さくなりcv errorも小さくなっていきますが,kが20を超えたあたりからcv errrorが少し高くなっているのがわかります.これはbiasが高くなっているからですね.
線形回帰との比較
このようにデータに対して柔軟にfitしてくれるkNN回帰ですが,線形回帰のような単純なモデルに制限されるより,このようなノンパラメトリックな手法の方が良さそうに思うかもしれません.
線形回帰とkNN回帰を比較した時,それぞれどういった利点/欠点があるのでしょうか?
ここでは一般的に言われることを列挙しておきます.
- 線形回帰の利点: 学習が簡単,解釈しやすい,仮説検定しやすい
- 線形回帰の欠点: モデルの形が既に決まっているので,真の\(f\)がそれと異なる場合に予測の精度が下がってしまう
- 真の\(f\)が線形の場合は線形回帰の方が精度がいいが,そうでない場合は大抵kNN回帰の方が精度が高い
- kNN回帰はノイズの特徴量があるとそれに引きづられて著しく精度が落ちる
実際には真の\(f\)がどんなものか分からないので,kNN回帰をまず実施するという人は多いと思います.また,真の\(f\)が線形であることはほとんどないのでkNN回帰の方が精度が高い結果を得られることが多いです.
が,機械学習では精度の高さだけでなく解釈性も求められることが多いので,多少の精度を犠牲にしても線形回帰の方が使いやすくて良いというのが一般的な考えかと思います.
線形回帰の方ができることが多いですからね!(多項式回帰やLassoなんかもできるし,p値を確認できたりしますからね)
まとめ
今回はノンパラメトリックな回帰アルゴリズムとしてkNN回帰を紹介しました.
- kNN(k最近傍法: k Nearest Neighbor)は分類器のアルゴリズムでよく使われるが,回帰でも使える(kNN回帰)
- kNNは数式モデルを使わないノンパラメトリックな手法で,そのためかなり柔軟にデータにfitする
- kNN回帰は予測データに最も近いk個の学習データの平均値を予測値とするアルゴリズム
- 大抵の場合線形回帰に比べ精度が高いが,解釈性が下がるため線形回帰の方が好まれやすい
今回の記事で回帰のアルゴリズムは一区切りをつけ,次の記事以降は分類問題について解説をしていきます.
分類問題は回帰問題と双璧をなす機械学習の分野なので是非このまま学習を進めていってください!
それでは!
追記) 次回の記事書きました!