データサイエンス入門の機械学習編第28回です.(講座全体の説明と目次はこちら)
追記)機械学習超入門動画講座を公開しました!動画で効率よく学習をしたい人はこちら(現在割引クーポン配布中です)
前回までの記事で,回帰,分類,クラスタリングの基本的なアルゴリズムとその評価指標を一通り学習しました.
今回以降の記事は,まだ紹介していないアルゴリズムについて扱っていきます.
実際にモデリングをする際には,基本的なアルゴリズムだけではなく,応用的なアルゴリズムで精度が出るかを試したり,より解釈しやすいモデルを選択したりすることになります.
今回は決定木と呼ばれる非常に有名なアルゴリズムを紹介します.決定木は解釈のしやすさから本当によく使われるアルゴリズムであり,さらにその応用をすることで非常に精度が高いモデルが作れたりもします.
今回の記事では回帰の決定木のアルゴリズムの基本を紹介し,今後の記事で決定木を応用しさらに高い精度のモデルを構築するやり方を紹介していきます.
それではみていきましょう〜!
目次
決定木とは?
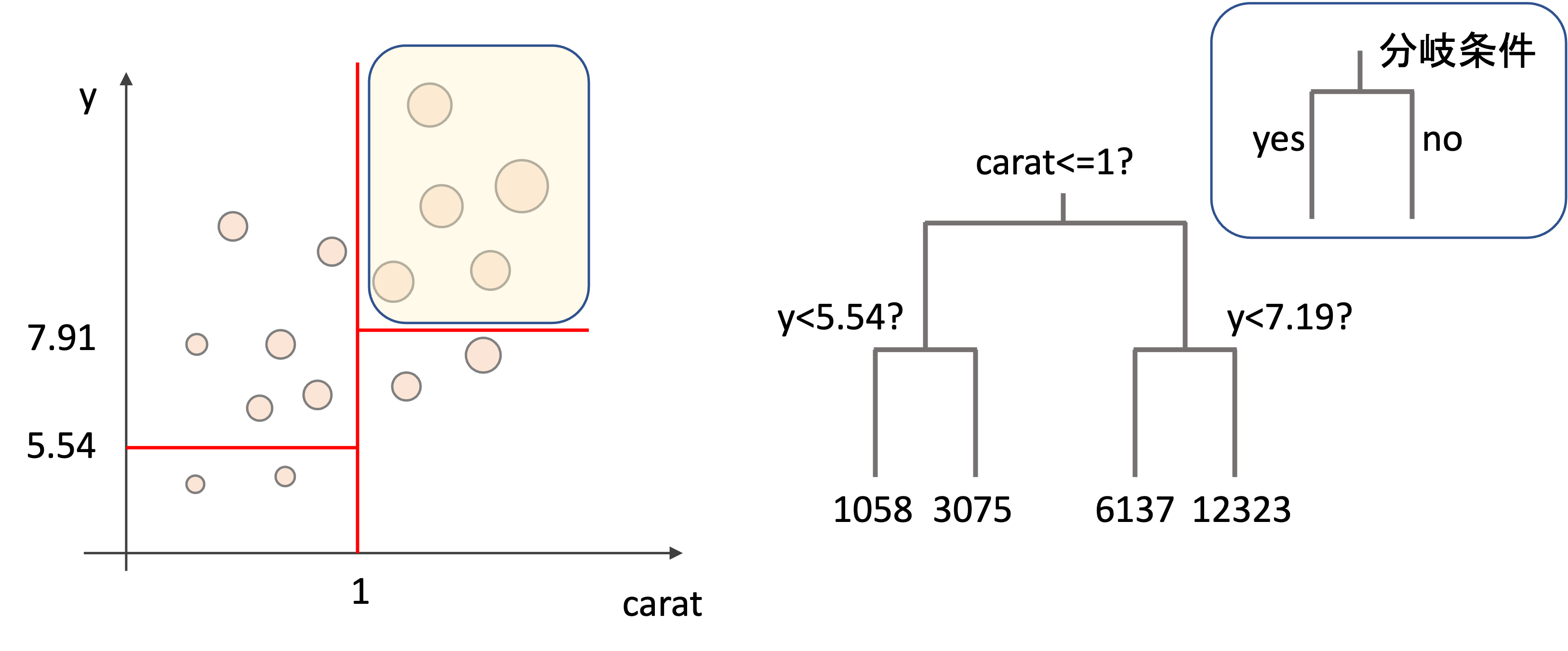
決定木(descision tree)は回帰でも分類にも使えるアルゴリズムで,以下のように木を逆さにした図がアウトプットとして出てきます.(今回は回帰の例を紹介していきます.)
分岐には条件が記され,その条件にそって最終的に予測値の決定を行います.
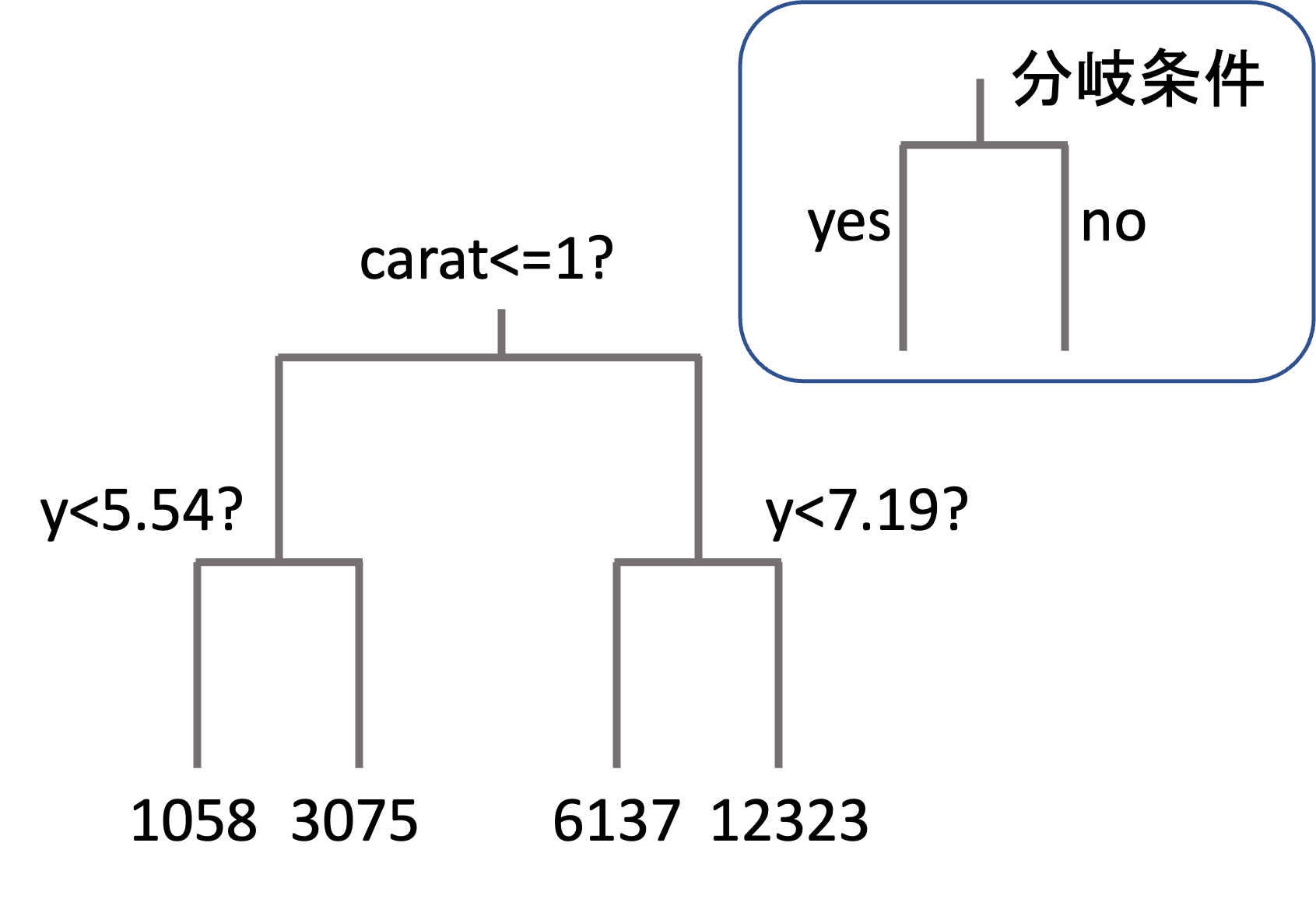
上図は第4回などで紹介したdiamondsデータセットを使った例です.carat(カラット数)や,x, y, zといったダイヤのサイズ(mm)の情報からダイヤの値段(price)を予測することを考えます.
この例ではカラット数が1を超えるかどうかで二分され,そのあとyの値(ダイヤの幅mm)がいくつなのかでさらに二分され,最終的に4種類の値(price: 値段)にたどり着いています.この最終的な値こそがモデルの予測値となり,この末端の箇所を「木」の比喩に擬えて「葉(leaf)」と呼んだりもします.
今回の例は2段階までの深さでしたが,もっと細分化させることもできます.

そうなんです.決定木はまさに人間が予測値を決定するプロセスに非常に近いので,とても解釈性があります.
今回の例では,カラットが1以上でyの値(ダイヤの幅)が7.19mm以上であれば$12,323(約150万円)と予測しているわけです.視覚的にも理解しやすいですね!
決定木アルゴリズム

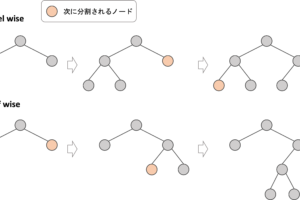
それでは,具体的にどのように決定木を作っていくのかをみてみましょう!決定木を作る流れは以下の通りです.文字では伝わりにくいので図解します
1.例えば以下のような学習データ(特徴量はcaratとy, 目的変数はprice(価格)です)に対して二つの領域に分ける(図はイメージです.実際の値とは関係ありません)
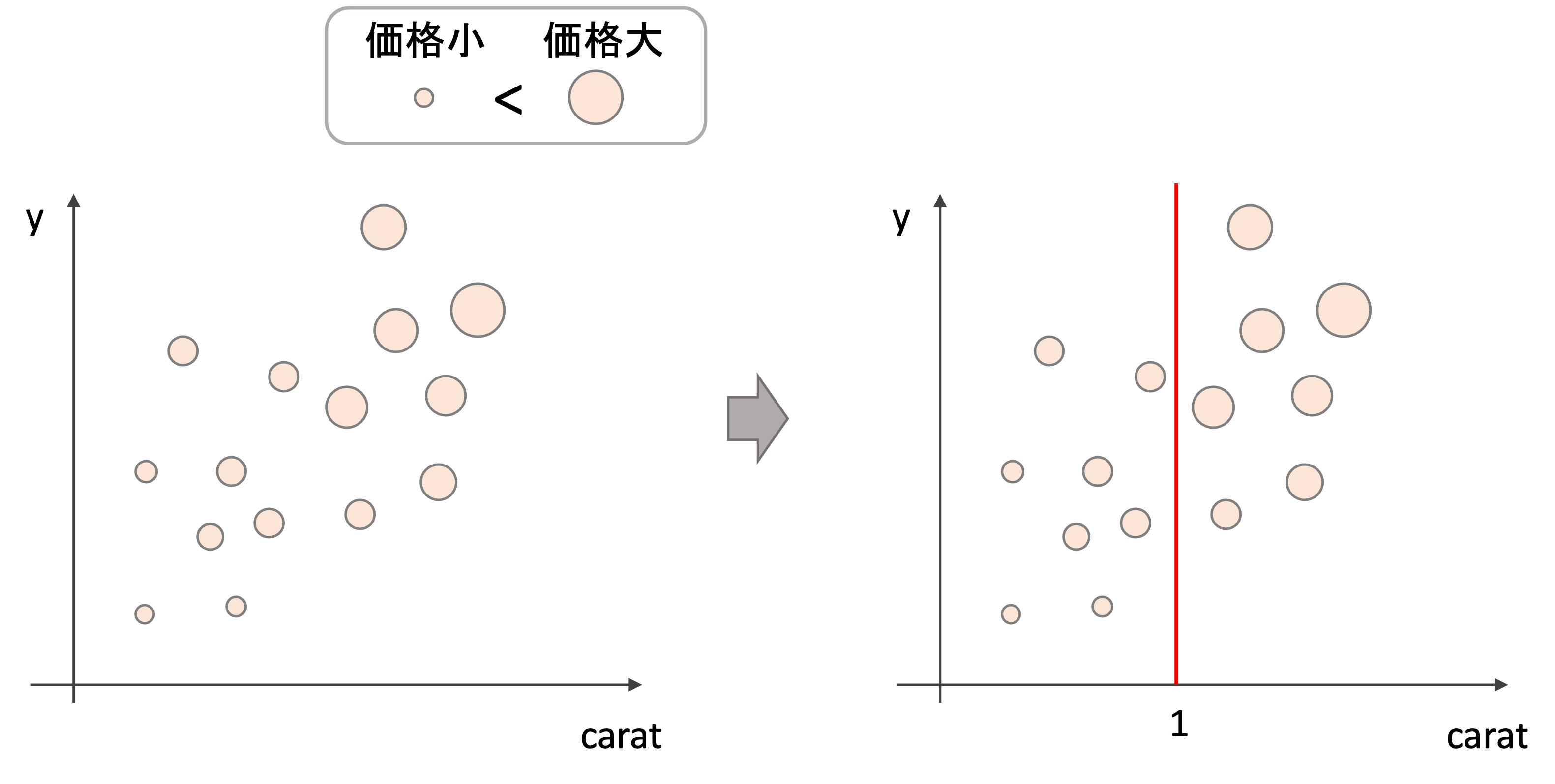
2.それぞれの領域をさらに二つに分ける
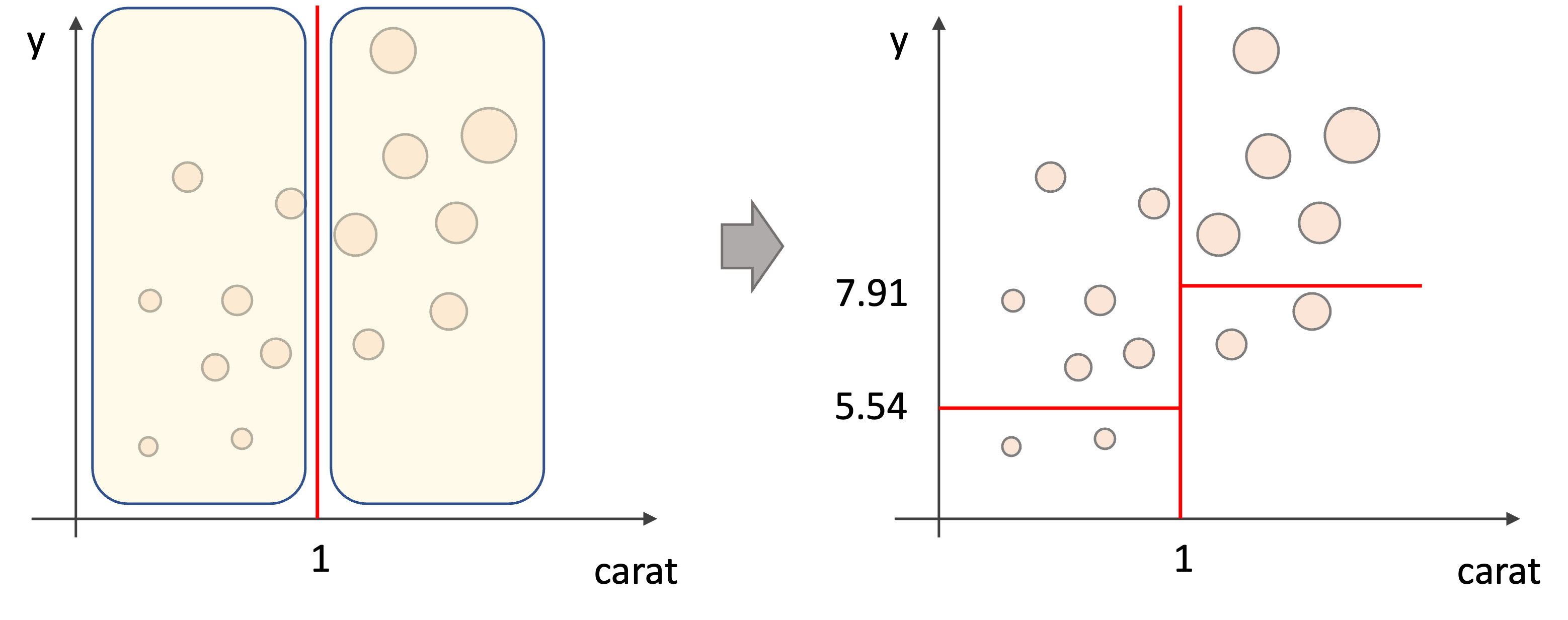
以上の2ステップを”ある条件”までそれぞれの特徴で繰り返していきます.”ある条件”は色々とありますが,例えば領域内のデータの数が一定数になったり,木の深さが一定数になったらやめます.
そして最終的にその領域にある学習データの値の平均値を予測値とします.
なので例えばテストデータが1カラットより大きく,ダイヤの幅(y)が7.91より大きい場合は以下の領域に属する学習データの平均値を予測値として使います.
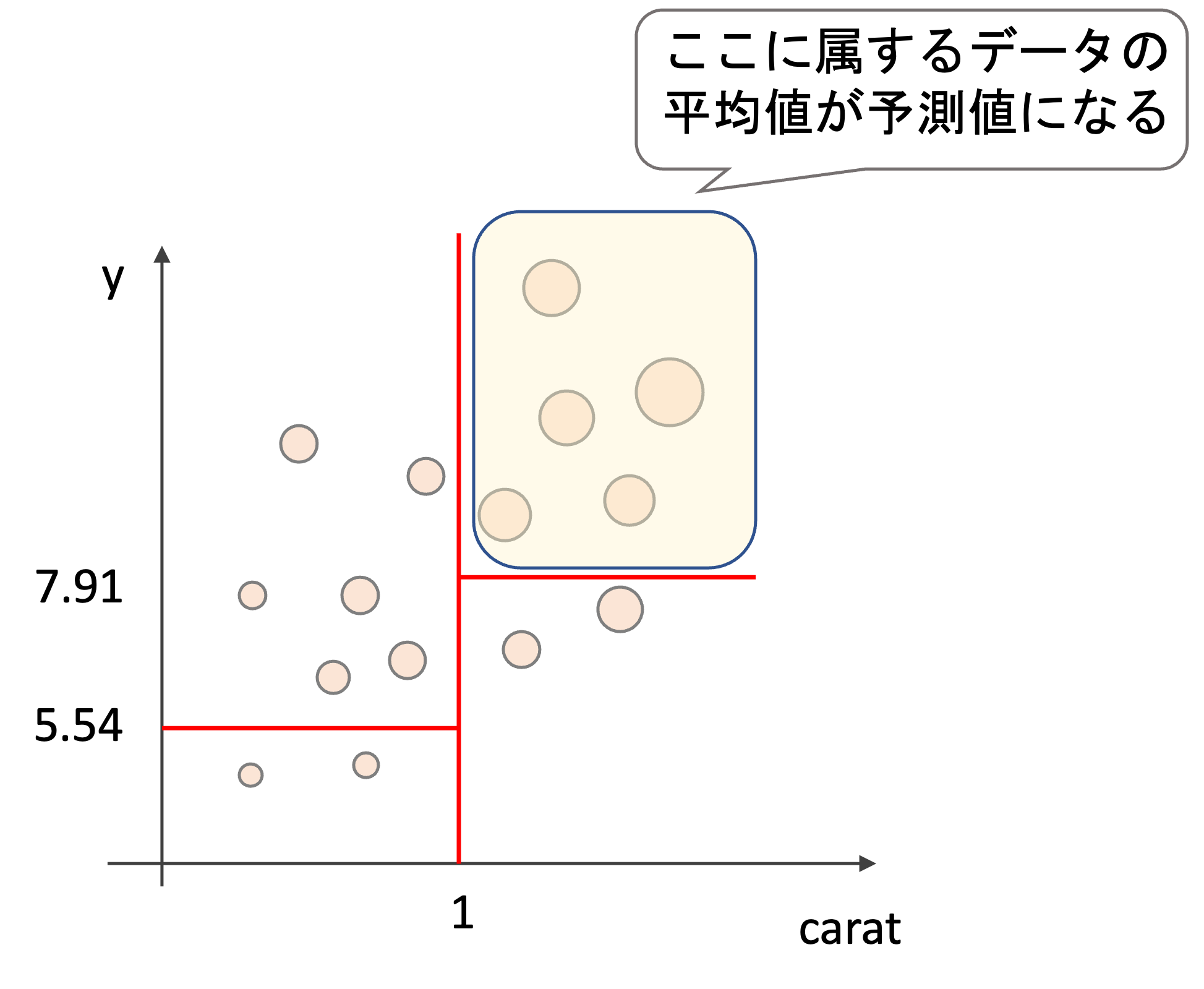
アルゴリズムの流れはめちゃくちゃシンプルですよね!分割する場合は常に2つに分割(binary split)することに注意しましょう.

色々やり方はあるのですが,回帰ではそれぞれの領域のRSS(residual sum of squares)の合計が最小になるように領域を作ることが多いです.(他にもmean absolute error(MAE)や他の指標を使うやり方もあります.)
領域\(R\)内のRSSは以下のように表すことができるので
$$RSS=\sum_{i\in R}(y_i-\hat{y}_R)^2$$
2分割する際にそれぞれの領域を\(R_1\),\(R_2\) とすると
$$\sum_{i\in R_1}(y_i-\hat{y}_{R_1})^2+\sum_{i\in R_2}(y_i-\hat{y}_{R_2})^2$$
が最小になるように領域を決定することになります.(ただし\(\hat{y}_R\)は領域\(R\)内の学習データの目的変数の平均で,この値が予測値になるため\(\hat{y}_R\)と表記しています.)
本来であれば,最終的にそれぞれの領域内でのRSSの全ての領域での合計が最小になるように領域を決定するのが望ましいですが,それだと計算量が高くなってしまうので,毎回の分割の際にRSSの合計が最小になるように領域を分割して行きます.なので,例えばその時は最適な分割だったとしても,後の分割の結果それが最適になるとは限りません
決定木の過学習
このアルゴリズムをひたすらに繰り返すと階層の深い複雑な決定木ができますが,複雑な決定木はvarianceが高く過学習となり汎化性能が低くなります.(biasとvarianceについては第12回を参照)
そのため,木が大きくなりすぎないように注意します.木が大きすぎると,精度が下がるだけではなく,決定木のメリットである解釈性も下がりますし,学習にすごく時間がかかるのです.
これを回避するには,木の深さをあらかじめ決めたり,葉に属するデータの最小数を指定し,それ以上分割を行わないようにしたりすることで回避することができます.
他にも,次回の記事で解説するcost complexity pruningという手法を使って木を小さくするやり方があります.
Pythonで回帰の決定木モデルを作る
それでは,Pythonでどのように回帰の決定木モデルを作れるのかをみてみましょう.
決定木も他の機械学習のモデル同様,scikit-learnにすでに用意されています.
回帰の決定木は sklearn.tree.DecisionTreeRegressor クラスを使います.
今回は先ほどのdiamondsデータセットの例を使ってみましょう.
データ準備
|
1 2 3 4 5 6 7 8 9 |
import pandas as pd import seaborn as sns from sklearn.model_selection import train_test_split df = sns.load_dataset('diamonds') df = pd.get_dummies(df, drop_first=True) X = df.loc[:, df.columns!='price'] y = df['price'] X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0) |
この辺りは本講座で何度も出てきているコードなので説明は不要かと思います.
理論上,決定木では質的変数はそのまま扱うことができ,特にラベル(0,1,2など)変換やone-hotエンコードは不要です. しかし,scikit-learnは文字列の特徴量をサポートしていないので,今回はone-hotエンコードを使ってダミー変数化しています.また,機械学習をする場合はどんなモデルにも対応できるようにするため前処理でダミー変数化することが多いので今回もそのようにしておきます.
決定木は特徴量ごとに分割していくので,特徴量間でスケールを合わせる必要がありません.そのため標準化を行っても結果は同じになるため今回は標準化は省きます
モデル学習
|
1 2 3 |
from sklearn import tree model = tree.DecisionTreeRegressor(max_depth=4) model.fit(X_train, y_train) |
インスタンス生成時にはいくつか引数を指定します.今回はよく使うものだけ紹介します.
- max_depth : 木の深さをintegerで指定します.なにも指定しない( None )と他の条件( min_samples_split など)やこれ以上分割できないところまで分割します.
- min_samples_split : intで指定した場合は分割する際に必要な最低限のデータ数で,floatを指定すると全データ数の割合で指定することができます.
- ccp_alpha : cost complexity pruningのalphaの値を指定します.これについては次回の記事で解説します.
なにも指定しないと最後まで分割をし複雑なモデルになり過学習します.また,時間もかかるので注意しましょう.
今回は max_depth=4 として学習させます.
予測
|
1 |
model.predict(X_test) |
決定木の可視化
決定木の最も重要なポイントは可視化です.可視化ができるから決定木をするといってもいいくらいですね!
色々とやり方はあるんですが,ここでは以下の2つのやり方を紹介します.
- tree.plot_tree()
学習済みのtreeモデルを引き数に渡します.そのまま実行するとみにくかったりするので,図やテキストの大きさを指定しておきます.また,戻り値には図の内容がテキストのリストで返ってきますが,特に不要なので _ に格納しておきます.
また, feature_names 引数には特徴量の名前のリストを入れます.今回は X.columns から持ってきます.
|
1 2 3 |
import matplotlib.pyplot as plt plt.figure(figsize=(40, 20)) _ = tree.plot_tree(model, fontsize=10, feature_names=X.columns) |
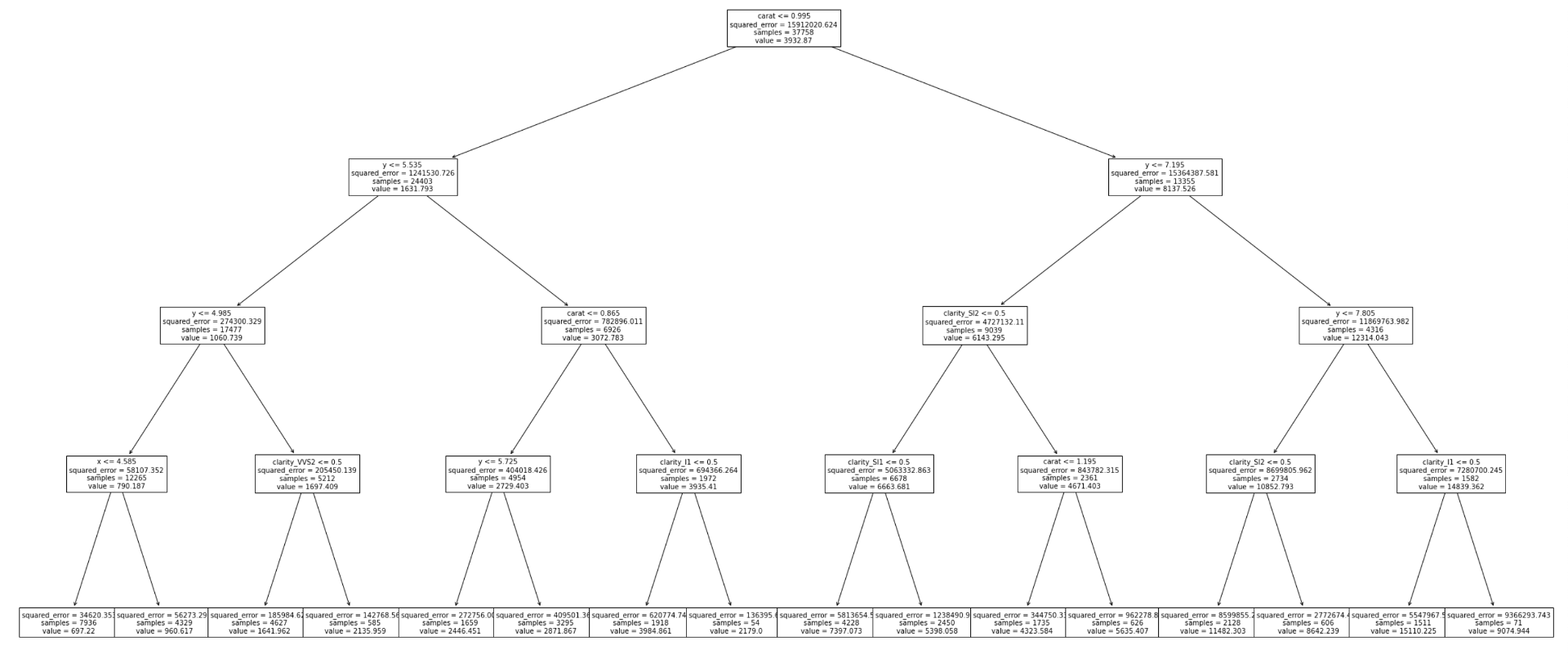
それぞれの分岐には条件と領域内のsquared errorの平均,sample数と予測値のvalue(領域内の学習データの目的変数の平均値)が記され,葉にも同様の値が記されているのがわかります.
これだと木が大きくなると見にくいので,以下のようにテキストで表示するのが良かったりもします
- tree.export_text()
|
1 |
print(tree.export_text(model, feature_names=list(X.columns))) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
|--- carat <= 1.00 | |--- y <= 5.54 | | |--- y <= 4.98 | | | |--- x <= 4.59 | | | | |--- value: [697.22] | | | |--- x > 4.59 | | | | |--- value: [960.62] | | |--- y > 4.98 | | | |--- clarity_VVS2 <= 0.50 | | | | |--- value: [1641.96] | | | |--- clarity_VVS2 > 0.50 | | | | |--- value: [2135.96] | |--- y > 5.54 | | |--- carat <= 0.87 | | | |--- y <= 5.72 | | | | |--- value: [2446.45] | | | |--- y > 5.72 | | | | |--- value: [2871.87] | | |--- carat > 0.87 | | | |--- clarity_I1 <= 0.50 | | | | |--- value: [3984.86] | | | |--- clarity_I1 > 0.50 | | | | |--- value: [2179.00] ~~以下省略~~ |
決定木の見方
決定木のアルゴリズムからわかるように,最初に分割する境界が最もRSSの合計を下げるようになっています.
つまり,決定木を見た時に上に来ている特徴量は,目的変数を予測するのにより重要である特徴量であることがわかります.
今回の例ではcaratが一番上にきていています.つまり,ダイヤの値段を決める最も重要な特徴量はcaratであると言えるわけです.
また,今回質的変数はdummy変数にしているので,0.5が境目になっていますが,<0.5ということは0, 0.5<ということは1であると見ていただいてOKです.
決定木と特徴
ここでは,簡単に一般的に言われている決定木の特徴を挙げておきます
- 他のモデルよりも一般的には精度が落ちる
- 人が決定するロジックに近いので,非常に解釈しやすい
- 解釈性が高いので,小さい木であれば機械学習を知らない人にも説明しやすい
- ロバスト性に欠ける.データに外れ値があったり,すこしデータが変わっただけで結果が大きく変わることがある
- 沢山の決定木を組み合わせることで精度の高いモデルを構築することができる(今後の講座で扱います)
まとめ
今回は回帰の決定木のアルゴリズムについて紹介しました.
- 決定木は回帰にも分類にも使える
- 決定木は木を逆さにしたような図になり,条件分岐を辿って行き最終的に結果を決める
- 人間の決定ロジックに近いため解釈性が高いが,一般的に他のモデルよりも精度が低い
- 各特徴量空間で領域を二分にすることを繰り返していく.この時,RSSなどの指標が小さくなるように分割していく
- 木が大きいと過学習になる恐れがあり,解釈性も下がり時間もかかるため,ある程度小さい木が望ましい
決定木は解釈性の高さから本当によく使われるモデルです.また,複数の決定木を組み合わせることでかなり精度の高いモデルが構築できることも知られています.
この辺りについてはまた今後の記事で解説しますが,次回は分類の決定木のアルゴリズムを紹介していきます!
cost complexity pruningという,複雑な木を避ける手法についても解説していくので是非このまま学習を進めていってください!
それでは!
追記)次回の記事書きました!