質的変数を説明変数として使う方法を解説(one-hot エンコーディングとダミー変数トラップ)【機械学習入門13】

こんにちは，米国データサイエンティストのかめ(@usdatascientist)です．

データサイエンス入門の機械学習編第13回です！(講座全体の説明と目次はこちら)

追記)機械学習超入門動画講座を公開しました！動画で効率よく学習をしたい人はこちら(現在割引クーポン配布中です)

今回は質的変数を説明変数として使う際に行う変換について解説をしていきます．

これにはone-hot エンコーディングと呼ばれる手法があるので，それを使います．

機械学習をする際には質的変数があるデータを扱うことがほとんどです．なので質的変数の取り扱いは必修事項なのできちんと今回の記事で学んでいきましょう！

質的変数と量的変数

今までの記事では，特徴量として「広さ」や「カラット」など，数値で表せる変数のみを扱ってきました．

しかし，実際に扱うデータには，数値ではない変数というのがあるはずです．例えば「男女」とか「血液型」とかですね．

このようなカテゴリーで表す変数のことを，カテゴリー変数や質的変数といい，一方数値で表せる変数のことを連続変数や量的変数といったりします．

質的変数は数値ではないのでそのまま機械学習のモデルに特徴量として使うことができません．

質的変数をうまく数値で扱えるようにするためにある工夫をする必要があります．

今回の記事では最も一般的なやり方であるone-hot エンコーディングというやり方を紹介します．非常に有名な手法でかつ，機械学習のモデル構築には必ずと言っていいほどでてくるのでしっかり押さえておきましょう！

one-hot エンコーディング

またなんだかとっつきにくいネーミング・・・

名前はとっつきにくいですが，やってることは非常にシンプルで合理的な処理なので理解できると思います！（機械学習あるあるですが，大したことしないのにやたら名前だけはいかついという．．．）

例えば，第１回の記事などで例に出した「家賃」を予測する回帰モデルを例にとってみましょう．

「広さ」を特徴量にした時の$y_i$のモデルは以下のようになるんでしたね

$$y_i=\theta_0+\theta_1x_i+\epsilon_i$$

ただし$x_i$は$i$番目のデータの「広さ」の値で，$y_i$は$i$番目のデータの「家賃」の値です．$\epsilon_i$は特徴量だけでは説明できない部分の誤差項です．

では例えば「ベランダ付き」という特徴量の場合はどうなるでしょうか？「ベランダ付き」の特徴量は，その物件にベランダがついているか，ついていないかです．

これはまさに質的変数ですね．このように質的変数を特徴量として扱う場合は以下のように考えます

(※今度は$x_i$を$i$番目のデータの「ベランダの有無」としています．)

$x_i$は$i$番目のデータの「ベランダ付き」の値ですが，ベランダ付きであれば「1」そうでなければ「0」としています．

このような変数を作ってしまえば質的変数も特徴量として使うことができます．このような変数のことをダミー変数(dummy variable)と言うので覚えておきましょう！

これは言い換えると以下のような形に変換していると言えます．(特徴量「ベランダが付いてない」は全て0になるので，特徴量として存在しない形になります)

では，これが複数の場合はどうなるかみてみましょう．同じ要領でできます．

例えば「向き」という特徴量があったとして「東向き」「西向き」「南向き」「北向き」の四つのカテゴリーをとりうる質的変数を考えます．この場合，以下のダミー変数を考えます．

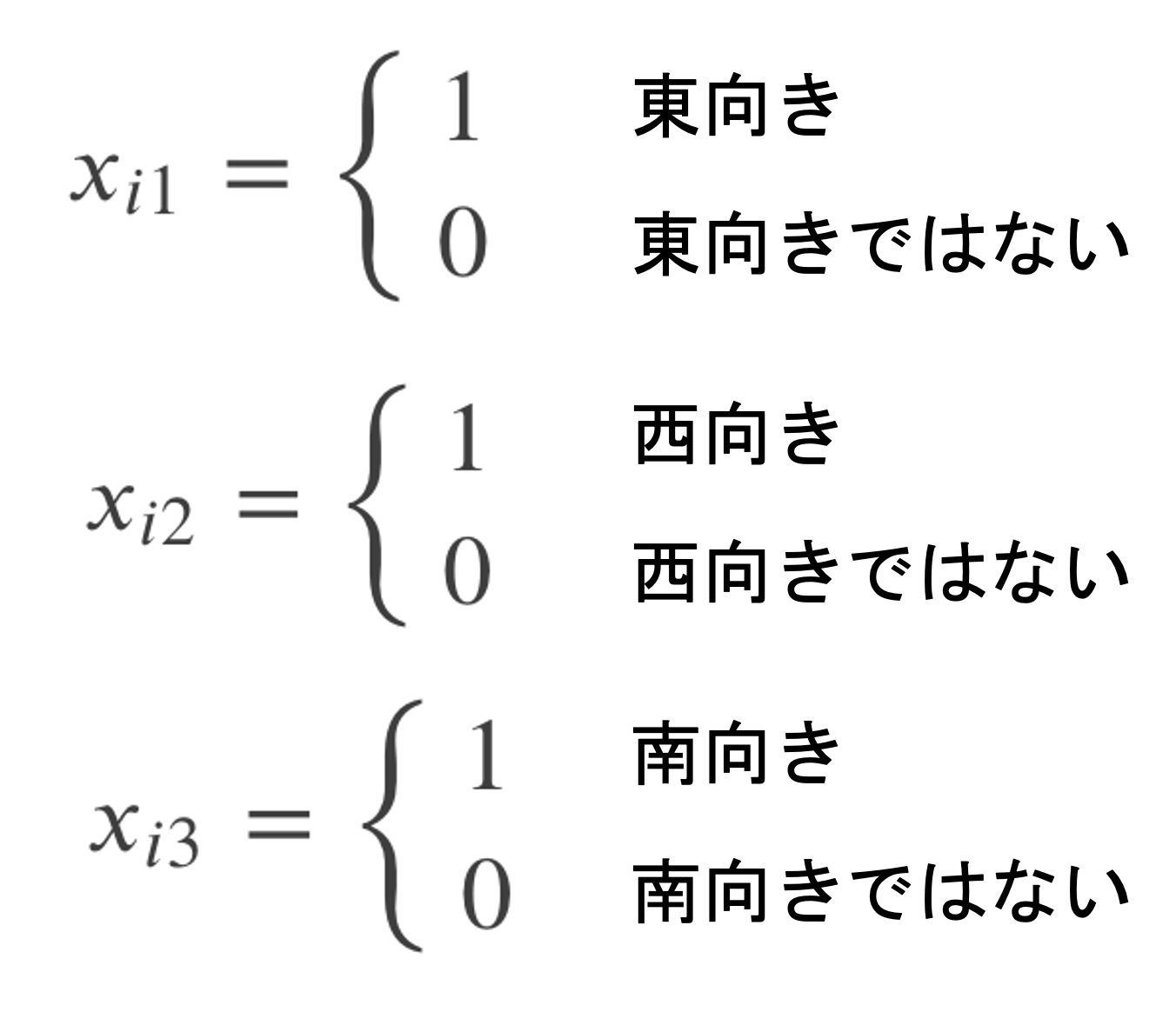
これらのダミー変数を使って$y_i$のモデルを考えると以下のようになるのがわかると思います．

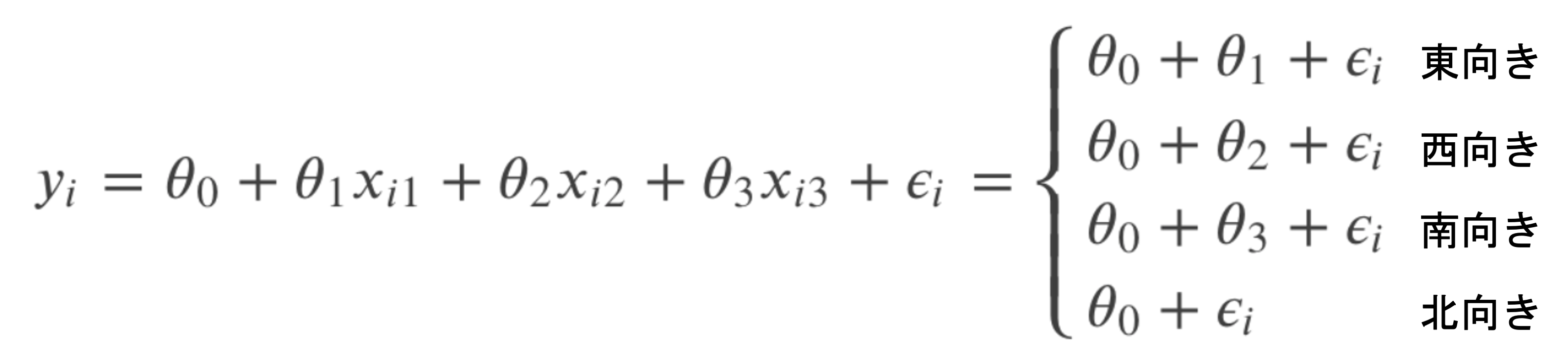
これは以下のようにそれぞれのカテゴリーを0と1で変換していると言えます．(特徴量「北」は全て0になるので，特徴量として存在しない形になります)

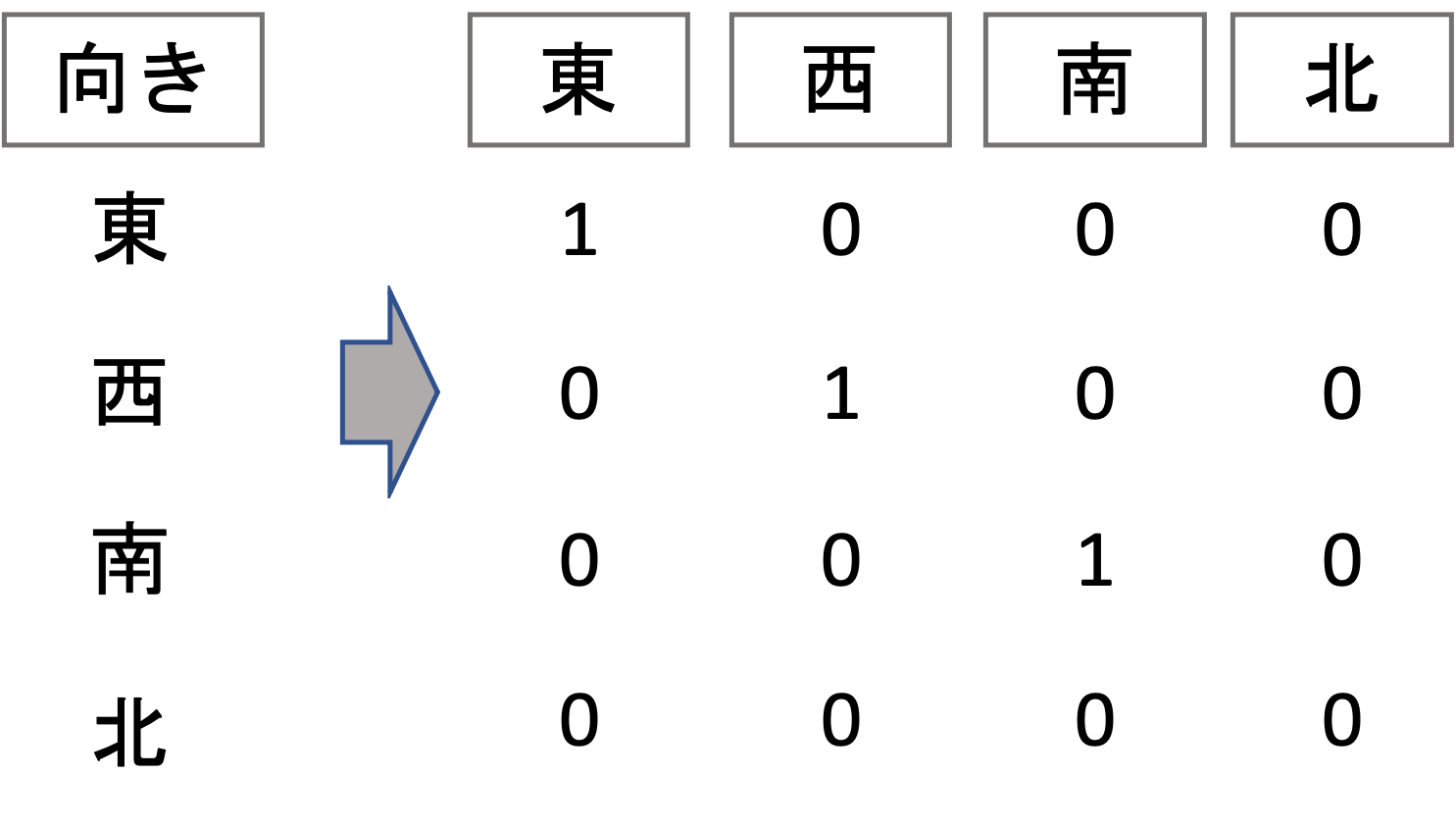
このように，カテゴリーのとりうる値の数だけ0と1で構成されるベクトルで表現し，そのカテゴリーだけ1(hot)で表すことから，one-hot ベクトル(one-hot encoded vector)と言い，このような処理をone-hot エンコード(one-hot エンコード)と言います．

補足
このように，データを一定の規則に基づいて「符号化」や「記号化」することをエンコード(encode)すると言います．今回はデータをone-hotのベクトルに符号化するのでone-hot エンコーディングといいます．

でも，ひとつのカテゴリーは全て0になるんだね

そうなんです．ここが初学者がone-hot エンコーディングで「？？？」になってしまうところだと思います．

これはダミー変数トラップ(dummy variable trap)と呼ばれる有名な罠(!?)です．

ダミー変数トラップとは

先ほどの「ベランダ付き」のダミー変数を考える際に，なぜ以下のようにしないのか疑問に思った方もいるでしょう

一見，上記のように$x_{i2}$を作ったほうが正しそうに見えます．が，これは実は大きな問題があるのです．

このようにすると，常に$x_{i1}=1-x_{i2}$の関係が出てしまい，二つの特徴量間に完全な相関が生まれてしまいます．

第4回でも述べたように，特徴量間に完全な相関があるとモデルを構築することができなくなってしまいます．(この問題はmulticollinearityと呼ばれます)

そのため，one-hot エンコーディングでダミー変数を作る際には，必ずカテゴリー数-1の数だけ作るようにします！(これをダミー変数トラップと呼びます．)

ダミー変数トラップは初学者の人が引っかかりやすいところなので注意しましょう！

Pythonでone-hot エンコーディングしてモデル構築してみる

それではPythonで実際に質的変数をone-hot エンコーディングして線形回帰モデルを構築してみましょう！

今回も，第4回以降何度も登場しているdiamondsデータセットを例にして， price を予測するモデルを作ることを考えてみましょう

import seaborn as sns
df = sns.load_dataset('diamonds')
df.head()

import seaborn as sns

df = sns.load_dataset('diamonds')

df.head()

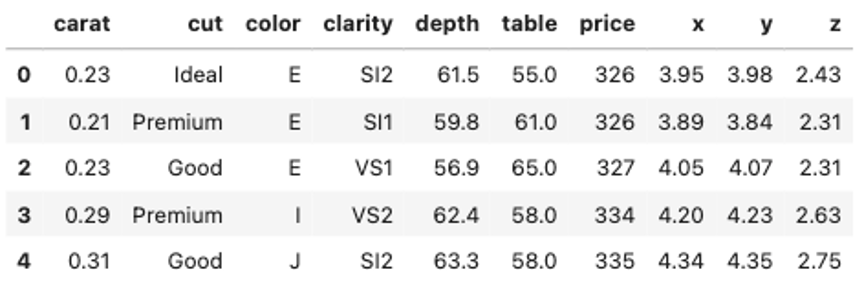
本データセットでは，”cut”, “color”, “clarity”が質的変数です．これらは当然ダイヤモンドの値段に影響があるはずです．

ではこれらをone-hotエンコーディングして，特徴量として使えるようにしましょう！

実は，DataFrameには非常に便利なメソッドが用意されています．pd.get_dummies()メソッドを使うことで，簡単にone-hotエンコーディグのダミー変数を作ることができます．

例えば”cut”カラムにのみダミー変数を作ってみましょう

cut カラムがとりうる値は，Seriesに対して .drop_duplicates() をcallすることで以下の5つであることがわかります．

df['cut'].drop_duplicates()

1	df['cut'].drop_duplicates()

0        Ideal
1      Premium
2         Good
5    Very Good
8         Fair
Name: cut, dtype: category
Categories (5, object): ['Ideal', 'Premium', 'Very Good', 'Good', 'Fair']

0 Ideal

1 Premium

2 Good

5 Very Good

8 Fair

Name: cut, dtype: category

Categories (5, object): ['Ideal', 'Premium', 'Very Good', 'Good', 'Fair']

pd.get_dummies() に，cutカラムのみのDataFrameを入れてダミー変数を作ってみます．

import pandas as pd
pd.get_dummies(df[['cut']])

1 2	import pandas as pd pd.get_dummies(df[['cut']])

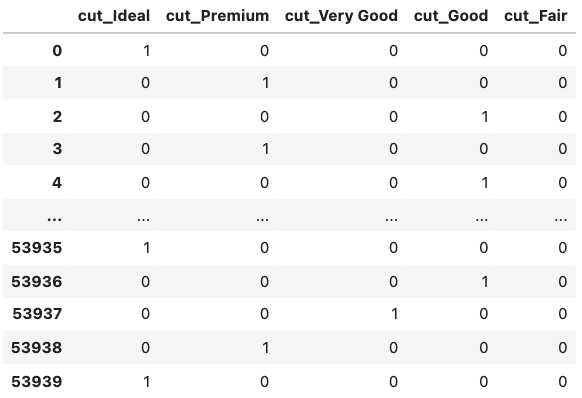
すると，このようなDataFrameを返します．cutのそれぞれの値がそれぞれの特徴量に変換され，0と1にエンコードされているのがわかります．

しかしこのままだと上述したダミー変数トラップの問題があるので， pd.get_dummies() に drop_first=True を入れてcallしましょう．すると，最初のカテゴリの値の特徴量を落としてくれます．

pd.get_dummies(df[['cut']], drop_first=True)

1	pd.get_dummies(df[['cut']], drop_first=True)

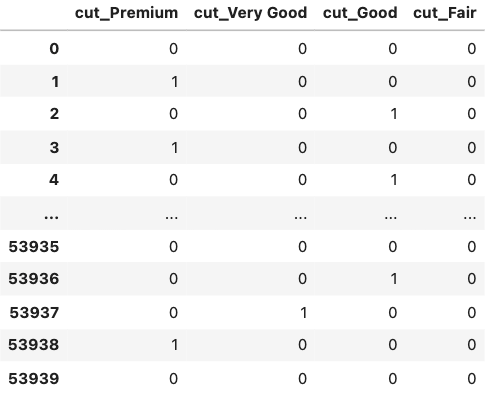
これで5つのcutカラムの値に対して4つのダミー変数ができました．

実際にはcut以外の質的変数も同様にダミー変数に変換するので，もとの df をそのまま引数に渡せばOKです．

df = pd.get_dummies(df, drop_first=True)
df.head()

1 2	df = pd.get_dummies(df, drop_first=True) df.head()

するとこんな感じで全ての質的変数をone-hotエンコーディングでダミー変数に変えてくれます！超便利ですよね！

この df を使って例えば以下のように5-foldCVで学習&評価することができます．

from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LinearRegression
import seaborn as sns

model = LinearRegression()

X = df.loc[:, df.columns!='price']
y = df['price']

cv = KFold(n_splits=5, random_state=0, shuffle=True)
scores = cross_val_score(model, X, y, scoring='neg_mean_absolute_error', cv=cv, n_jobs=-1)
print(np.abs(np.mean(scores)))

from sklearn.model_selection import KFold

from sklearn.model_selection import cross_val_score

from sklearn.linear_model import LinearRegression

import seaborn as sns

model = LinearRegression()

X = df.loc[:, df.columns!='price']

y = df['price']

cv = KFold(n_splits=5, random_state=0, shuffle=True)

scores = cross_val_score(model, X, y, scoring='neg_mean_absolute_error', cv=cv, n_jobs=-1)

print(np.abs(np.mean(scores)))

740.5483989635775

1	740.5483989635775

興味がある人は，質的変数を全て除いた場合と比較してみてください！以下に参考コード載せておきます．

from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LinearRegression
import seaborn as sns

model = LinearRegression()

df = sns.load_dataset('diamonds')
# include all fields
# df = pd.get_dummies(df, drop_first=True)
# X = df.loc[:, df.columns!='price']
# include only continuous field
X = df.loc[:, ~df.columns.isin(['price', 'cut', 'clarity', 'color'])]
y = df['price']

cv = KFold(n_splits=5, random_state=0, shuffle=True)
scores = cross_val_score(model, X, y, scoring='neg_mean_absolute_error', cv=cv, n_jobs=-1)
print(np.abs(np.mean(scores)))

from sklearn.model_selection import KFold

from sklearn.model_selection import cross_val_score

from sklearn.linear_model import LinearRegression

import seaborn as sns

model = LinearRegression()

df = sns.load_dataset('diamonds')

# include all fields

# df = pd.get_dummies(df, drop_first=True)

# X = df.loc[:, df.columns!='price']

# include only continuous field

X = df.loc[:, ~df.columns.isin(['price', 'cut', 'clarity', 'color'])]

y = df['price']

cv = KFold(n_splits=5, random_state=0, shuffle=True)

scores = cross_val_score(model, X, y, scoring='neg_mean_absolute_error', cv=cv, n_jobs=-1)

print(np.abs(np.mean(scores)))

まとめ

今回は質的変数を特徴量として扱うための変換であるone-hotエンコーディングという手法を紹介しました．質的変数の変換は他にもあるんですが，もっともポピュラーなやり方がone-hotエンコーディングなので，これさえ押さえておけば問題ないかと思います！

one-hotエンコーディングは，質的変数がとりうる値の数-1個のダミー変数に変換する．0と1(hot)の値を取ることになるため”one-hot”と呼ばれる
質的変数がとりうる値の数分ダミー変数を作ってしまうと，ダミー変数間に完全な相関が生まれてしまい学習がうまくいかなくなるので，常に「とりうる値の数-1個」のダミー変数を作るようにする(ダミー変数トラップ)
Pandasの .get_dummies() にDataFrameを入れるだけで簡単にone-hotエンコーディングによるダミー変数を作成することができる．引数 drop_first=True を入れることでダミー変数トラップを回避できる

質的変数を特徴量に入れたいケースはかなり多いので，しっかり覚えておきましょう！次回以降のレクチャーでは，特徴量を取捨選択するやり方を紹介します！質的変数を特徴量として使えるようになると，特徴量の数が多くなっていって「本当にこれ全部必要なの？」と思うでしょう．実際には不要な特徴量のせいで精度があまり出ないこともあります．

特徴量選択は機械学習のメインテーマのひとつです．しっかり学んでいきましょう！

それでは！

追記) 次回の記事書きました！