Pythonで学ぶデータサイエンス入門:統計編第23回です!
(追記)全16時間の統計学動画講座を公開しました!☆4.8の超高評価をいただいている講座です.こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください.
久々のブログ更新です.前回の更新から半年以上経ってしまいました...
(ただサボってた訳ではありません.Git動画講座やPython動画講座を作成するのに時間がかかってしまいました...)
さて,今回の記事から本格的に推測統計の分野に入っていこうと思います!今までの内容は,推測統計を学習するために必要なベース知識だと思ってください.
これからが統計学の本番!
目次
推測統計とは??
第一回の記事でも触れましたが,推測統計は母集団に興味があります.母集団から抽出した標本を使って母集団の特性を推論していきます.
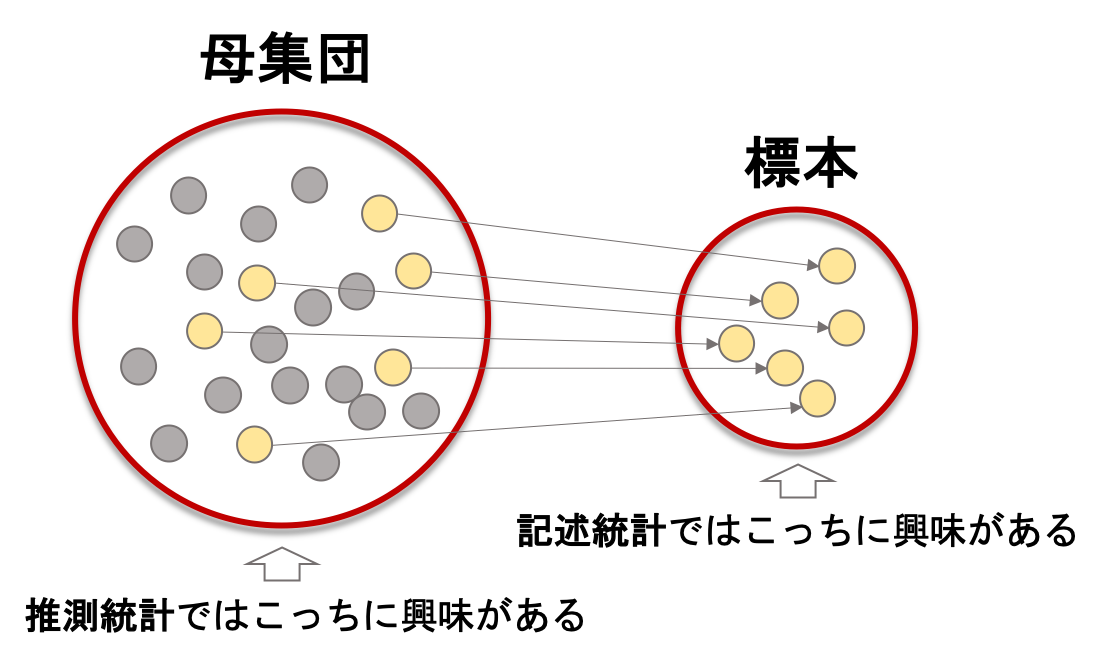
「標本という限られた情報を使って,母集団の特性を推測することができる」というのは,現実の世界においてあらゆる場面で役立ちますよね?
例えば日本全国の成人男性の平均身長を測るのに,全成人男性の身長を測っていくわけにはいきません.
ある工場で生産したPCの落下精度を測るのに,その工場で生産した全てのPCを落下させるわけにはいきません.
製品の不良率を測る場合,興味があるのは過去に作られた製品ではなくて将来作られる製品です.
とにかく,「母集団」というのは概念的なものだったり,全て調べることができないケースがほとんどです.
そこで役に立つのが”統計学”なんですね! 推測統計の分野を学習することで,限られた標本からその標本の背後にある母集団の特性を推定できるようになります.
推測統計の理論は「標本は母集団から無作為抽出された集団」を前提にしています.ですが,実際に無作為抽出を実行するのは簡単ではないのが実情です.
例えば全国の小学生の知能テストの結果の特性を推定するのに,あらゆる小学校からランダムに学生を抽出することはできません.なので,ある市区町村から小学校をいくつかランダムに選ぶなどできる範囲で標本を作ります.
その場合,「無理のない範囲で母集団を設定する」ことが重要になってきます.例えば全国ではなく特定の市の小学生に母集団を絞るとか.
特定の小学校での標本で全国の小学生の特性を推測するのは無理がありますからね!
推定と検定
推測統計には大きく,二つのタイプがあります.推定(estimation)と検定(statistical test)です.

推定というのは,標本から計算された値をもとに母集団の特性を推定するものです.(例えば,全国の成人男性の平均身長を標本の平均から推定するなど)
こちらの記事にも書きましたが,母集団の特性値を推測するために使われる標本の値を統計量と言い,推定に使う統計量を推定量(estimator)と言います.
また,母集団の特性値を母数といいます.”母数”はよく使われる用語なので覚えておきましょう.
検定というのは,漢字検定の検定とはだいぶ意味合いが異なります笑
母集団の性質に対しての「ある想定」について,標本の観察結果によってその想定が正しいと言えるかどうか,矛盾しないかどうかを調べる作業です.
少し難しいように聞こえますが,例えば「全国成人男性の平均身長は170cmである」という想定に対して,標本を観察してみると「どうやら170cmではなさそうだ」というのを確率的に調べることができます.
この”想定”のことを“仮説”(hypothesis)といいます.検定に使う統計量を検定統計量や単に検定量と言ったりするので,このあたりの用語も頭の片隅に入れれたら◎です!
今回の記事からは特に推定について扱い,検定については講座の後半で扱います!
点推定と区間推定
推定にも二つ,点推定(point estimation)と区間推定(interval estimation)というものがあります.点推定は,標本からの一つの推定量で母数をバシッと推定するもので,区間推定は「この区間に含まれるだろうな」とふわっと推定するやり方です.
基本的な考え方として,点推定でバシッと推定できたらいいけど実際には点推定で確かなことはいえないから区間推定である程度の幅をきかせて推定します.
つまり,点推定は実際にはあまり使われず,点推定の延長線上にある区間推定を使って推定するのが一般的です.
ということで本講座では区間推定について詳しく解説をしていきます!
区間推定のやり方
前述した通り,推定により母数を推測することができます.つまり,母集団の平均や比率,分散などを推測することができます.
これらの母数を推定するのに標本の推定量を使っていくわけですね!
推定したい母数のよって使う推定量は様々ですが,大まかな手順は以下の通りです.
- 母集団から無作為抽出した標本を作成する(実際にはすでに標本が用意されているケースが多いです.その場合は,このステップで母集団を設定しましょう)
- 標本から推定量を計算する(推定量は推定したい母数によって決まります)
- 推定量でバシッと母数を推定したいが,ドンピシャで当たることなんてないので,区間を設ける(この区間のことを信頼区間といいます.「例えば95%はこの区間に入る」など.詳細は次回以降の記事で解説します.)
- 推定量の標本分布を考える(標本分布についてはこちらの記事で詳しく解説しています.)
- その信頼区間がとりうる値を標本分布から算出する
大まかにいうとこんな感じです.このステップを終えると,「母数の値は〇〇%の信頼区間で△〜□の間である」と言えるようになります.
例えば「成人男性の平均身長は168cm〜172cmの間であることが95%確かである」のような感じです.つまり,95%はその間にあるし,5%は誤ってると言った具合

いきなり手順だけ説明されてもわからないと思うので,次回以降の記事で実際に区間推定をしてみたいと思います! 何度か実際にやってみると,すぐに覚えられるようになります.
まとめ
今回は推測統計の導入ということで文字だらけになってしまいましたが,今回の記事のまとめは以下です.
- 推測統計には大きく推定と検定がある
- 推定とは,母集団の特性値(母数)を母集団から無作為抽出した標本を使って母数を推定すること
- 検定とは,母集団の性質についての仮説を,標本を使って矛盾しているかどうかを調べること
- 推定には点推定と区間推定がある
- 点推定は標本の推定量を使ってバシッと母数を推定するもので,実際にはそんなドンピシャで推定できないので通常は区間推定を使う
ステップについては覚える必要はありません.何度かやっていくと自然に身につくと思います.
次回の記事では早速母集団の”比率”を区間推定してみたいと思います!
それでは!
追記)次回の記事書きました!