(追記)全16時間の統計学動画講座を公開しました!☆4.8の超高評価をいただいている講座です.こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください.
前回の記事から区間推定について連載しています.今回は平均の区間推定をわかりやすく解説します.
比率同様,母集団の平均を推定したいというのはよくあるケースだと思います.
全国成人男性の平均身長や平均体重を知りたい.ある工場で生産された部品の平均強度を知りたい.野菜の市場平均価格がしりたい.etc…
基本的な手順は前回の記事の比率の推定と同様です.なので,前回の記事をちゃんと理解していると楽に読み進められると思います!
目次
区間推定の鍵は標本分布
前回の比率の時もそうでしたが,区間推定で重要なのは「標本分布がどうなるか?」です.
標本分布さえわかれば,あとは信頼区間を設定して値を算出するだけです.
平均の区間推定をするには当然標本平均を使うわけですが,標本平均の標本分布はどのような分布になるのかを考える必要があります.そのあたりを意識して今回の記事を読み進めていただければと思います!
平均の区間推定をステップ毎に解説!
第23回で解説した区間推定のステップ通りに平均の区間推定をしてみましょう.
今回は一般化した形で書いていきます.(記事の後半でPythonを使って具体的な数値を入れていきます)
1. 母集団から無作為抽出した標本を作成する
母集団の平均を\(\mu\)(ミュー)とし,標本の大きさを\(n\)とします.
2. 標本から推定量を計算する
前回の記事で書いた通り,標本平均は母集団平均\(\mu\)の不偏推定量です.今回は標本平均を\(\bar{x}\)としましょう.
3.信頼区間を決める
標本平均\(\bar{x}\)だけで母集団平均\(\mu\)を点推定するのは心許ないので,信頼区間を設定し区間推定することを考えます.今回も前回同様95%の信頼区間を設定すればいいでしょう.
4. 推定量の標本分布を考える
ここがポイントです.標本平均の標本分布はどうなるのでしょうか?
第7回で述べた通り,標本平均\(\bar{x}\)の標本分布の平均は,母集団平均\(\mu\)と一致し,標本平均\(\bar{x}\)の標本分布の分散は母集団の標準偏差\(\sigma\)を使って\(\frac{\sigma^2}{n}\)(↓の図の\(\frac{\sigma}{\sqrt{n}}\)は標準偏差)と表せます.(この辺り非常に重要なので押さえておいて下さい.忘れてる!という方は第7回をもう一度読みましょう.)
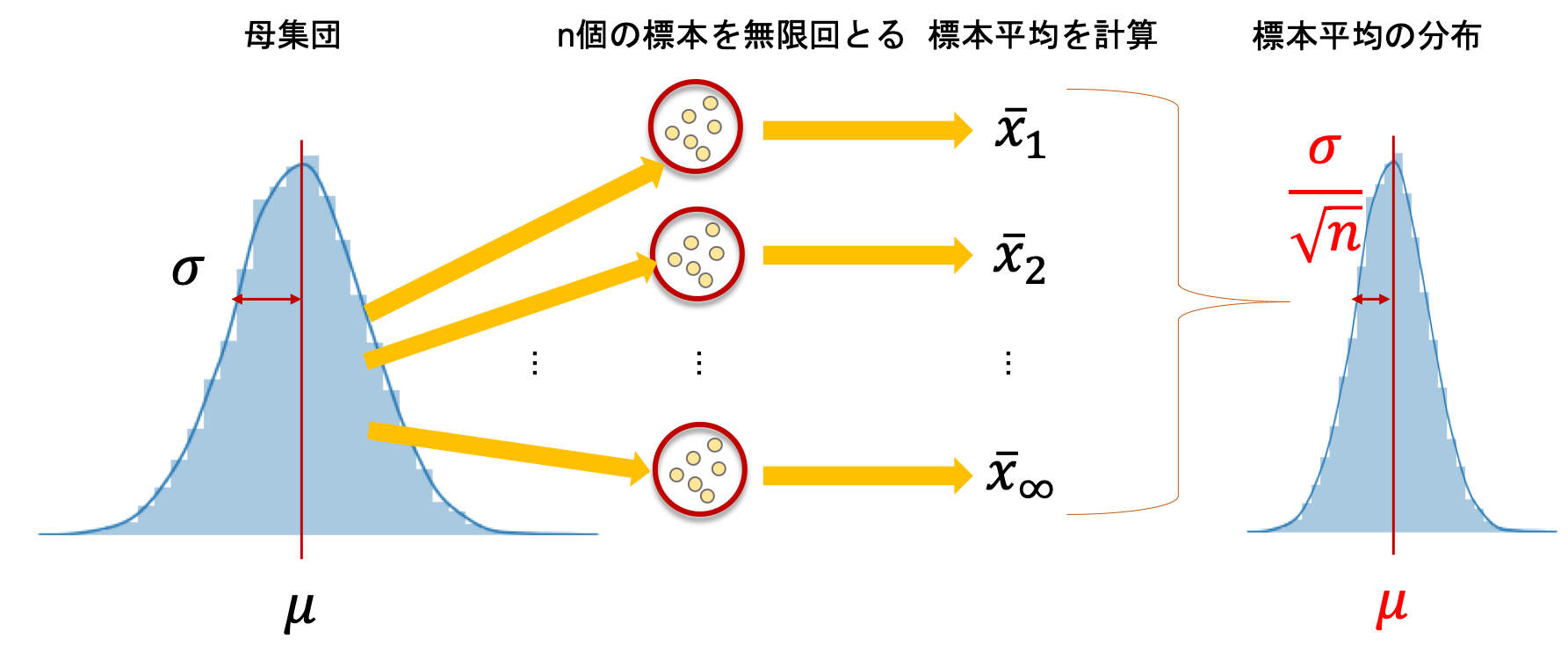

標本平均の標本分布の平均と分散はわかってるんですが,どういう分布になってるかはわからないのです.
母集団が正規分布であれば標本分布も正規分布になる(これは容易に想像できるかと思います)のですが,母集団が正規分布ではないとき標本分布はどのような分布になるのでしょう?
実は,標本の大きさ\(n\)が十分に大きければ,標本平均\(\bar{x}\)の標本分布は正規分布に近似することができます.
つまり,母集団の分布がどんな分布であろうと,\(n\)を大きくすると標本平均\(\bar{x}\)の標本分布は正規分布になるんです!
正規分布恐るべしです.本当にいろんなところで出てきますね.この定理のことを中心極限定理と言います.統計学の理論上非常に重要な定理なので覚えておきましょう!
つまり,
1. 母集団が正規分布であれば,標本の大きさ\(n\)によらず標本平均\(\bar{x}\)の標本分布は正規分布である
2. 母集団が正規分布でなくても,標本の大きさ\(n\)が十分大きければ標本分布は正規分布に極めて近くなる
ということがいえるわけですね.
今回の記事では,\(n\)が大きいと仮定して,標本分布は正規分布とみなせるケースを考えてみましょう.
\(n\)が大きい時,標本平均\(\bar{x}\)の標本分布は平均\(\mu\)の分散\(\sigma^2/n\)の正規分布になります.この分布で95%の区間を計算すれば母集団平均が95%信頼区間でとりうる値の区間を算出することができます.
前回の記事同様,標準化して考えましょう.標準正規分布の形にもってくれば「95%区間が-1.96〜1.96」という数値を使えますからね.\(\bar{x}\)から平均\(\mu\)を引いて標準偏差\(\frac{\sigma}{\sqrt{n}}\)で割れば,標準正規分布に従う\(z\)を計算できます.
$$z=\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n}}}$$
5. その信頼区間がとりうる値を標本分布から算出する
では,95%の確率で上記の\(z\)がとりうる値を計算してみましょう.標準正規分布では-1.96〜1.96の間に95%のデータが含まれているので(第8回参照)
$$-1.96<\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n}}}<1.96$$
これを\(\mu\)に対して計算して値を出していけばOKです.

そうです.上記の式には母集団の標準偏差である\(\sigma\)が入ってしまっています.通常母集団の標準偏差なんてわからないですよね?(母集団の平均\(\mu\)がわからないから推定しようとしているのに,母集団の標準偏差\(\sigma\)がわかるはずがありません.)
そこで,ここでは母集団の標準偏差\(\sigma\)の代わりに標本標準偏差\(s’\)を使います.標本標準偏差\(s’\)は不偏分散\(s’^2\)の平方根をとればOKです.不偏分散\(s’^2\)は第6回で解説したとおり,以下の式で表されます.
$$s’^2=\frac{1}{n-1}\sum{(x_i-\bar{x})^2}$$
なので,上記の式は
$$-1.96<\frac{\bar{x}-\mu}{\frac{s’}{\sqrt{n}}}<1.96$$
となり,これを\(\mu\)についての式に変形すれば
$$\bar{x}-1.96\frac{s’}{\sqrt{n}}<\mu<\bar{x}+1.96\frac{s’}{\sqrt{n}}$$
となります.
母集団標準偏差\(\sigma\)の代わりに標本標準偏差\(s’\)を使ったことで, 標準化後の標本分布は標準正規分布ではなく,少し変形した分布になります.これをt分布と言いますが,t分布は\(n\)が大きければ標準正規分布に近似できます.これについては次の記事で詳しく解説します

一つ一つちゃんと手順を追っていけばそんなに難しい数式ではないですが,これらの数式は覚えなくてもいいと思います.
推測統計で重要なのは手順です.例えば,母集団が正規分布でなく\(n\)が小さいにもかかわらず標本分布に正規分布を使っていたら,それは間違った推定になってしまいます.
きちんと理論を理解しないと正しい推定はできませんし,その結果を正しく解釈することはできません.
理論をきちんと理解した上で,計算はツールに任せましょう!
実際に平均の区間推定をやってみよう!
前回の記事同様,scipyのstatsモジュールの各確率分布に対して .interval() を使えばOKです.
今回は実際のデータセットで平均の区間推定をやっていきましょう!
使うデータセットはなんでもいいです.自分が興味のあるデータセットをKaggleなどから取ってきましょう!(Kaggleについてはこちらの記事で紹介しています.登録していない方は是非登録しましょう.無料で色々なデータセットにアクセスできるようになります.)
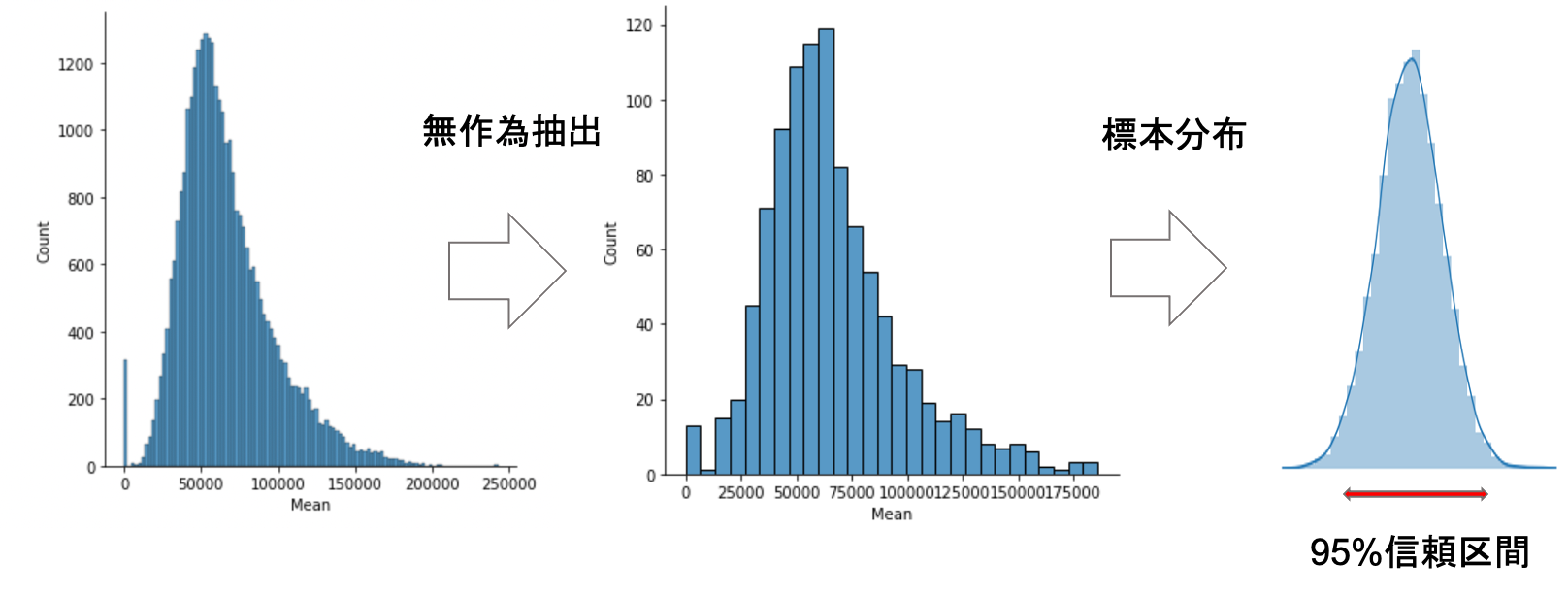
本記事では,US Household Income Statisticsのデータセットを使って,米国内の地域別の世帯収入の平均値のデータを見ていきたいと思います.(各レコードは,”地域別の収入平均”になっていることに注意しましょう.)
それではデータをDownloadして,csvファイルをPandasのDataFrameにロードしてみましょう!(この辺りはデータサイエンスのためのPython講座第11回に詳しく書いているので参考にしてください!)
|
1 2 3 4 5 |
import pandas as pd import seaborn as sns %matplotlib inline df = pd.read_csv('kaggle_income.csv', encoding="ISO-8859-1") |
今回のデータセットでは encoding 引数を指定しないと
|
1 |
'utf-8' codec can't decode byte 0xf1 in position 2: invalid continuation byte |
というエラーになってしまいます.(データの中に,utf-8でデコードできない文字があると怒られてしまいます.)
この辺りは適宜ググって,適切なencodingを指定してください.多くの場合 encoding="ISO-8859-1" を指定すればデコードできます.
df.head() でデータセットを見てみると....
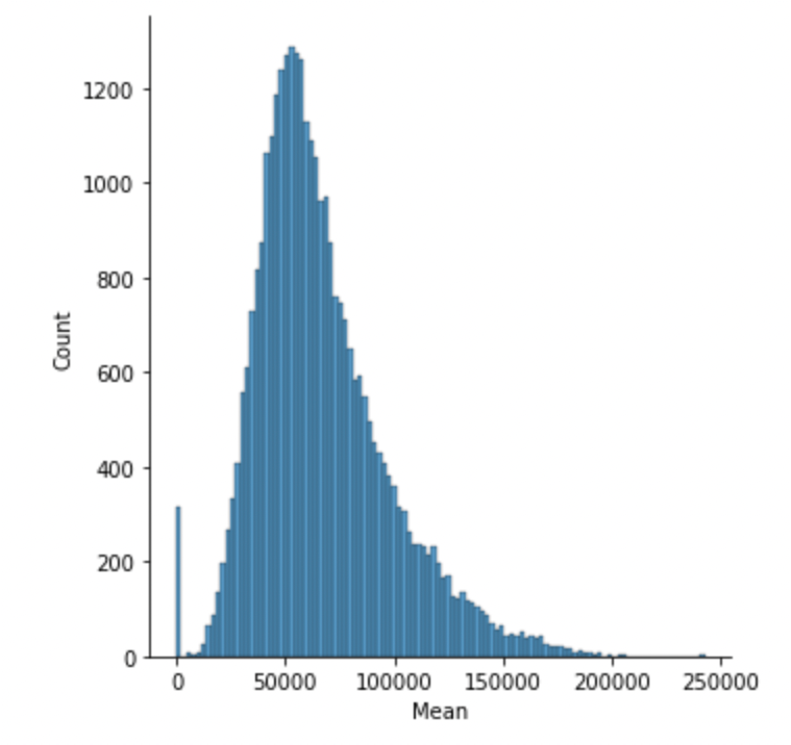
このようなデータセットであることがわかります.それぞれのレコードが地域(例えば”Alabama州のMobile CountyのChickasawCity”)を表していて,その地域での平均世帯収入がMeanカラムにあります.
では早速Meanカラムの分布を見てみましょう.
|
1 |
sns.displot(df['Mean']) |
この辺りのseabornの使い方については,データサイエンスのためのPython講座第24回を参考にしてください.
また,データサイエンスのPython動画講座でデータのvisualizationについてかなり詳しく解説しているので,是非受講してみてください.☆4.7以上の超高評価いただいています.(記事の方に割引クーポンを記載している場合があるので確認してください.)
最新のseabornでは .distplot() はdeprecated(つまり将来なくなる)のwarningがでるため,.displot()を使ってください. 少し前のseabornだと .displot() は実装されていないので,その場合は .distplot() を使ってください.
今回はこの分布を母集団の分布とします.明らかに正規分布ではないですね.収入などの金額のデータは正規分布にならないことがほとんどです.(外れ値などもあるかと思いますが,今回は無視して進めていきます)
それでは,Meanカラムの平均を見てみましょう.(つまりこれが,今回推定したい母集団の平均となります.通常これは未知の値であることに注意しましょう)
|
1 2 |
import numpy as np np.mean(df['Mean']) |
|
1 |
66703.98604193568 |
すると,約$66kであることがわかります.(700万円くらいでしょうか?)
今回のケースは,全米国の地域別の世帯収入の平均をとっていますが,この平均の平均が米国の全世帯の平均になるかというと, そうはなりません.
例えば小学校AとBで同じテストをしたとき,小学校Aの生徒100人の平均点が60点で,小学校Bの生徒50人の平均点が70点だった時,150人の平均は(60 + 50)/2 = 55点とはならないですよね?正しく平均値を出すには(100×60 + 50×70)/150 = 63.3点とする必要があります.
このように,それぞれの値の重さ(100人と50人)を考慮して計算する平均を加重平均と呼びます.
今回の例では,単純に全地域別の平均の平均をとりたいだけなので,加重平均は不要です
さて,それでは区間推定のステップに沿って実際に平均値の推定をしてみましょう!(今回推定する母数は$66703です.)
1. 母集団から無作為抽出した標本を作成する
df から無作為にデータを抽出して標本を作ります.母集団
df は32526件あるようなので今回は1000件をランダムに選んで標本とします.
DataFrameからランダムにデータを選択するには, .sample(n) を使えばOKです.( n には標本の大きさが入ります. frac に0~1の値を入力して割合を指定することもできます.)
|
1 2 |
n=1000 sample_df = df.sample(n=n) |
一応分布も見てみましょうか
|
1 |
sns.displot(sample_df['Mean']) |
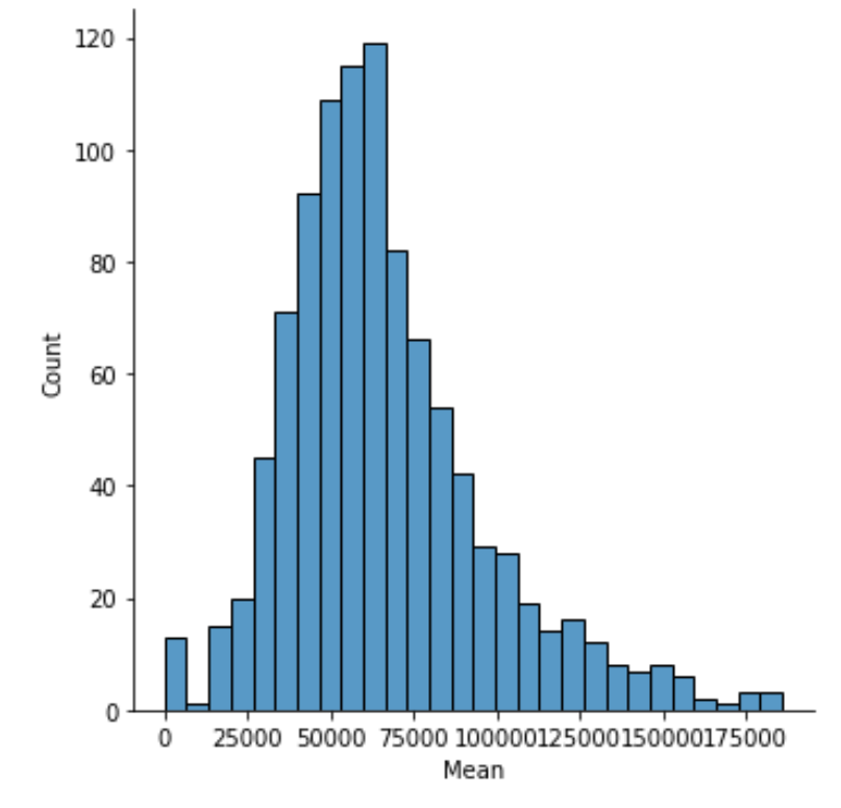
母集団のそれと似ていると思います.(以降,標本はランダムに抽出しているため,みなさんのお手元の値と異なる場合があります.)
2. 標本から推定量を計算する
今回推定したいのは母集団の平均値なので,推定量に使うのは当然標本平均ですね.
母集団と同様に標本の平均を見てみましょう
|
1 |
np.mean(sample_df['Mean']) |
|
1 |
65102.071 |
$65102という結果になりました.母集団の平均は$66703なので,少し金額が低く出ています.
3.信頼区間を決める
今回も95%信頼区間で計算します.
4. 推定量の標本分布を考える
標本平均の標本分布は,母集団が正規分布であれば標本の大きさ\(n\)によらず標本分布も正規分布になるんでした.
今回の母集団の分布は正規分布ではありません.
通常,母集団分布がどのような分布になっているかはわからないですが,ある程度予測することはできます.自然界にあるものは大抵正規分布とすることができるでしょう.例えば成人男性の身長,ある花の茎の太さ,また,工場で生産した製品の誤差などは正規分布とできそうです.一方,年収や企業の利益など,金額が絡むようなデータは正規分布ではないと予測できます.今回も世帯収入についてのデータなので,やはり正規分布と考えるのは無理があります.
では母集団の分布が正規分布ではない場合標本分布がどうなるんだったかというと,標本の大きさ\(n\)が大きければ中心極限定理により正規分布に近似できるんでした.
では,今回のn=1000というのは十分大きいと言えるのでしょうか?
これについてはまた次の記事で詳しく解説しますが,答えはYesです.n=1000は標本分布を正規分布に近似するのに十分大きいサイズです.
では,前回の記事同様にstatsモジュールの .interval() メソッドを使って推定をしてみましょう.
今回使用する確率分布は,平均\(\bar{x}\)・分散\(\frac{\sigma^2}{n}\)の正規分布です.正規分布は stats.norm を使えばいいのですが,母分散\(\sigma^2\)はわからないので,代わりに不偏分散\(s’^2\)を使って以下のようにすればOKです.( alpha に信頼区間0.95, loc に分布の平均\(\bar{x}\), scale に分布の標準偏差\(\frac{s’}{\sqrt{n}}\)を入れます)
|
1 2 3 4 |
from scipy import stats sample_mean = np.mean(sample_df['Mean']) sample_var = stats.tvar(sample_df['Mean']) stats.norm.interval(alpha=0.95, loc=sample_mean, scale=np.sqrt(sample_var/n)) |
|
1 |
(63302.127654258715, 66902.01434574129) |
不偏分散\(s’^2\)は第5回でやった通り, stats.tvar() でOKです.
結果を見てみると,$63302〜$66902とあるので,95%の確からしさで母平均が$63302〜$66902にあるという推定ができました!
実際の母平均は$66703なので(ギリギリですが)この推定はあっていると言えます.
米国の全ての地域の世帯収入を調べなくても,ランダムにいくつかの地域(今回は1000地区)の世帯収入を調べれば,ある程度推定できたわけですね!
実際はt分布(!?)を使う
中心極限定理により母集団の分布によらず,標本サイズが大きい場合,平均の標本分布は正規分布とすることができるんでした.
ただ,それは母集団の分散が既知の場合です.母集団の分散は普通はわからないので代わりに標本の不偏分散を使ったんですよね?
しかし,不偏分散を使うが故に少し正規分布と違う分布になってしまいます.(標本サイズが大きい場合,やはり正規分布として近似することができます.なので,今回は気にせず正規分布として進めていきました)
この「母分散の代わりに不偏分散を使ったことで少し正規分布と違った形になった分布」をt分布と呼びます.
このt分布は今後の検定でも重要な役割を担う分布になるので,また次の記事で詳しく解説をしたいと思います!
まとめ
今回も長くなってしまいましたがまとめです!
今回の記事では平均の区間推定のやり方を解説しました.
- 母集団の平均を推定するには標本平均を標本推定量として使う(標本平均は母平均の不偏推定量である)
- 母集団が正規分布のとき,平均の標本分布も平均\(\mu\)・分散\(\frac{\sigma^2}{n}\)の正規分布になる(\(\mu\)は母平均,\(\sigma\)は母標準偏差)
- 母集団が正規分布ではなくても,標本の大きさが大きければ平均の標本分布も平均\(\mu\)・分散\(\frac{\sigma^2}{n}\)の正規分布になる(中心極限定理)
- 母集団の標準偏差\(\sigma\)は未知なので,代わりに標本標準偏差\(s’\)を使う
- これによって標本分布が正規分布と異なる形になってしまう.これをt分布(詳しくは次回の記事で解説!)という.標本が十分大きければこれも正規分布として近似できる.
- 平均の区間推定には stats.norm.interval() を使う
平均の区間推定をするポイントは以下の3つです.
- 母集団の分布は正規分布か?
- 母集団の分散は既知か?
- 標本サイズはいくつか?
標本分布が正規分布になり,母集団の分散が未知であればt分布を使うことになります.今回は大標本を想定したので,t分布ではなく正規分布で進めていきました.
t分布は非常に重要な確率分布なので,また次の記事で詳しく解説していきます!
それでは!
(追記)次回の記事書きました!